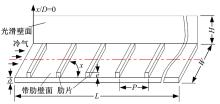
试验装置示意图如图1所示, 其主要由蒸汽发生器、试验段、短路加热器、排气装置以及数据采集系统等组成。试验中将短路加热器的电极直接固定在试验段的两端, 采用低电压(0~7.5 V)、大电流(0~4500 A)的方式对通道壁面的加热量进行调节, 并用硅酸铝纤维纸包裹试验段和相邻管道, 以减少试验段与周围环境的热交换。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 试验装置示意图Fig.1 Schematic diagram of experimental apparatus

试验件为模化的某重型燃机第一级导叶内冷通道的单元带肋通道, 通道厚度 δ为3 mm, 材质为普通304不锈钢, 图2给出了试验件的结构示意图。试验研究的厚壁矩形带肋通道的结构参数如下:通道长 L、宽 W和高 H分别为1024 mm、80 mm和40 mm; 宽度方向的两个壁面内部具有扰流肋片; 肋高 e为2.5 mm; 肋片与通道内主流方向的夹角 α为90° ; 肋间距 P为25 mm。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 试验件的结构示意图Fig.2 Schematic diagram of structure of test section

试验测试时, 试验段进出口放置了两个直径为3 mm的E型热电偶(精度为0.5 ℃), 用于测量蒸汽流进、出口温度; 试验段外壁面沿中心线上焊接了80个0.5 mm直径的E型软体热电偶(精度为0.5 ℃)。通道进、出口设置了静压测孔, 用于测量试验段的压差。在试验段来流前稳定段处使用流量计测量蒸汽流量, 使用总压探针测量入口蒸汽的总压。

通道进口雷诺数 Re可由下式计算得出:

Re=ρuD/μ(1)

式中: ρ为冷气参考温度下的密度; u为通道进口处冷气的平均速度; D为通道水力直径, 本文中D=53.33 mm; μ为冷气的动力黏度。

试验段内壁面的平均热流密度 q可以根据短路电加热器的加热功率以及系统散热损失计算出, 其计算公式如下:

q=(UI-Qloss)/Sin(2)

式中:S_in为试验段内壁面总面积; U为短路电加热器电压; I为短路电加热器电流; Q_loss为散热损失, 主要包含试验件的辐射热量和传导到隔热材质的热量。根据通道进、出口冷气参数的测量值计算得到冷气的吸热量, 结合试验时电加热器的加热功率, 可以计算出试验系统的散热损失 Qloss[13]。

单元带肋通道内壁面当地的努赛尔数 Nu为:

Nu=qD/(Tw-Tf)λ(3)

式中:T_w为内壁面当地温度, 是根据传热学原理, 由测量的外壁面温度值计算得出的近似值; T_f为根据进出口蒸汽温度线性插值得到的当地温度; λ为当地的蒸汽导热系数。

光滑圆管壁面努塞尔数为^[14]:

Nu0=0.023Re0.8Pr0.4(4)

式中:Pr为蒸汽的普朗特常数。

通道的摩擦因数可以定义为:

f=ΔpD/(2ρΔLu2)(5)

式中: Δp为通道两测点之间的压差; ΔL为通道两测点之间长度。

通过综合性能因子 F来评价带肋通道的流动及换热的综合性能, 其表达式为:

F=(Nu/Nu0)/(f/f0)1/3(6)

光滑圆管的摩擦因数 f0的计算公式为^[14]:

f0=(1.58lnRe-3.28)-2(7)

试验段采用短路电加热的方式, 可将其视为均匀发热的大电阻, 其单位体积发热量 Q为:

Q=(UI-Qloss)/V(8)

式中: V为试验段总体积。

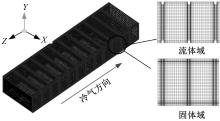
依据试验段加热方式及试验工况, 建立含有内热源项的耦合传热计算模型, 计算域含有流体域和固体域, 如图3所示。固体域视为各向同性的均质内热源固体, 只求解含有内热源项的能量方程, 如下所示:

∂(ρscpT)∂t∇·(λs∇T)+Q(9)

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 耦合传热计算模型Fig.3 Conjugate calculation model

式中: ρs、cp和 λs分别为304不锈钢的密度、定压比热和导热系数。依据ASTM标准, 304不锈钢的密度为7930 kg· m^-3, 定压比热为0.502 Jžkg^-1žK^-1; T为通道入口蒸汽温度; ∇T为温度梯度。

为了获取更加准确的试验段内壁面的温度, 考虑了温度对304不锈钢导热系数的影响。其导热系数计算公式如下:

λs=0.009471T+14.0614(10)

对于流体域, 采用基于有限元的有限差分法离散控制方程, 通过全隐式耦合多重网格, 应用ANSYS CFX求解三维可压缩的雷诺时均N-S方程, 采用标准k-ε 、SSG和SST k-ω 湍流模型计算流体的温度。方程中扩散项、源项和对流项的离散使用高精度离散格式, 整体残差收敛水平为10^-6。流体域为蒸汽, 蒸汽热物性参数采用CFX内置的标准IAPWS-IF97材料库中的steam2, 并根据通道内蒸汽工况范围选定压力和温度的上、下限。

计算模型采用结构化网格, 近壁面附近区域采用网格加密技术, 第一层网格至壁面的距离为0.001 mm, 网格增长率为1.2, 这样近壁面网格无量纲距离小于1。为保证数值方法的可靠性和精确性, 经过网格无关性验证, 流体域和固体域的总网格数为230万及以上时计算得到的带肋壁面努塞尔数的变化在2%以内, 因此本文采用的总网格数为230万。图4为90° 厚壁带肋通道耦合传热计算模型的网格示意图。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 网格模型示意图Fig.4 Schematic diagram of grid model

基于试验数据设置边界条件:将固体域和流体域对应的壁面设置为耦合面; 通道固体外壁面为绝热壁面。计算时, 固体域和流体域通过该耦合面传递等量的热流量和温度。流体域进口设置总压和温度, 出口给定流量。

值得注意的是, 在计算 Nu时, q取为厚壁带肋通道内壁面当地热流密度, 其他数值结果与试验数据处理方式相同。

本文开展了5组工况的厚壁带肋通道蒸汽冷却基础试验, 试验的具体工况如表1所示, 表中, p0为通道入口蒸汽总压; Ph为加热功率。

表1

Table 1

表1(Table 1)

表1 测试工况 Table 1 Test conditions 工况 Re p0/kPa T/K Ph/W 1 10455 296.90 442.96 288.86 2 19157 300.21 446.66 706.19 3 29805 299.43 448.17 1207.49 4 40246 299.15 448.98 1866.48 5 49635 298.38 451.19 2293.32

表1 测试工况 Table 1 Test conditions

图5和图6分别给出了不同工况下厚壁通道带肋外壁面温度和努塞尔数的试验值沿主流流向的分布。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 厚壁通道带肋壁面温度分布Fig.5 Temperature distributions on ribbed walls of thick-wall channel

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 通道带肋壁面当地努塞尔数沿流向分布Fig.6 Local Nu distributions on ribbed walls of channel along flow direction

从图5可以看出:通道壁面温度沿主流方向逐渐升高, 这是因为冷却蒸汽在流过通道的过程中不断地被加热, 其温度被提升、冷却性能变差而引起的; 由于试验只能测量通道外壁面的温度值, 加之304不锈钢的导热系数很大, 通道壁面较厚, 带肋内壁面温度在传递到外壁面时已经被均匀化, 以至于通道带肋壁面的肋片处没有出现温度的极低值, 温度沿主流流向的分布也较平缓, 没有出现周期性的波动。从图6可以看出:由于入口效应, 努塞尔数在通道入口段较高, 随着流动的发展其值缓慢降低, 直至基本保持不变, 也没有出现周期性波动。

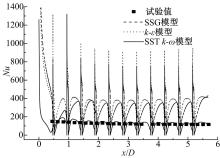
图7为工况3时不同湍流模型下通道带肋内壁面中心线上当地努塞尔数沿流向的分布曲线。由图7可知:由于带肋通道的入口效应和气流在肋片间的分离和再附着,

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 工况3时带肋内壁面当地努塞尔数沿流向的分布Fig.7 Local Nu distributions on ribbed walls along flow direction at case 3

计算的厚壁通道内壁面当地努塞尔数曲线呈现周期性的拱形分布, 而试验值沿主流流向的变化趋势比较平缓, 没有体现出拱形分布。这是因为热电偶布置不足, 以及试验数据处理时通道内壁面当地温度和当地热通量无法准确获得而造成的。从图7中还可以看出:在入口效应影响的0< x/D< 3区域, 拱形峰顶的努塞尔数沿流向迅速衰减, 接着气流进入湍流充分发展状态, 拱形峰顶的努塞尔数趋于稳定。肋片顶部靠近上游侧对流传热最为强烈, 在各拱形之间有尖锐的凸起, 其努塞尔数高出拱形峰值数倍。总体上, 努塞尔数沿主流流向逐渐衰减, 这是因为蒸汽流在通道内逐渐被加热, 冷却能力沿流向会逐渐变弱的缘故。

在所使用的湍流模型中, SSG和k-ε 湍流模型的预测值比试验值高出了很多; SST k-ω 湍流模型的计算结果与试验结果最接近, 误差在5%以内, 即SST k-ω 湍流模型可以较准确地模拟带肋通道中的流动和换热情况。因此, 本文后续内容皆采用SST k-ω 湍流模型进行计算。

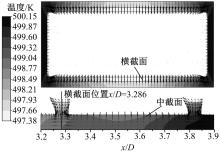
图8分别给出了通道壁厚为3 mm时, 通道横截面(x/D=3.286处)以及3.2≤ x/D≤ 3.9区域与带肋壁面垂直的中截面上固体域的温度和热流密度矢量分布。从图8中可以看出:固体截面上的温度和热流密度分布都很不均匀, 由于固体三维导热效应, 固体中的热量并不是沿着壁面的法向传入流体的; 在横截面上, 热量从通道相邻壁面夹角处的高温区域流向带肋面中部的低温区; 在中截面上, 在肋片及其附近区域, 肋片的左上角由于直接受到冷却流体的冲刷而温度最低, 热流密度最大, 而且肋片上大部分的热量传入了其上游的冷却流体, 只有少部分传入下游流体; 在肋片之间区域也出现了温度极小值, 肋片之间区域上游和下游的热流密度矢量方向都指向中部温度较低的区域。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 通道截面上温度及热流密度分布Fig.8 Temperature and heat flux distributions on channel sections

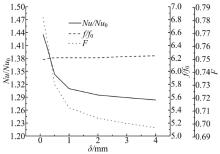
图9给出了通道壁厚为0.1~4 mm时, 带肋壁面上平均努塞尔数比、摩擦因数比和综合性能因子的分布曲线。从图9中可以看出:带肋壁面平均努塞尔数比和综合性能因子随着通道壁厚的增大先较快后缓慢地降低, 而通道的摩擦因数随着壁厚的增大基本保持不变。这是因为随着带肋通道壁厚的增大, 通道的传热热阻也相应地增大, 从而使得通道的换热系数降低。经计算, 壁厚从0.1 mm增大到4 mm时, 通道的换热系数和综合性能因子分别降低了10.6%和10.8%。综合来讲, 壁面厚度对带肋通道流动及换热性能的影响较小。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 壁厚对通道内蒸汽流动及换热性能的影响Fig.9 Influence of wall thickness on flow and heat transfer performance of steam in channel

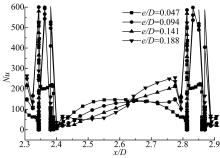
图10为肋高比为0.047~0.188时, 通道带肋壁面当地努塞尔数的分布曲线。从图10中可以看出:在肋片的下游区域, 通道带肋壁面换热系数随着肋高比的增大而依次减小; 在肋片的上游区域以及肋片区域, 通道带肋壁面换热系数随着肋高比的增大而依次增大。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 不同肋高比时带肋壁面当地努塞尔数分布Fig.10 Local Nu distribution at different e/D on ribbed wall

图11为不同肋高比时, 通道带肋壁面上平均努塞尔数比、摩擦因数比和综合性能因子的分布曲线。从图11中可以看出:通道壁面平均努赛尔数比随着肋高比的增大而增大, 这是因为随着肋高比的增大, 主流流体分离后产生的漩涡扰动不断增大, 使得流体流动的边界层厚度减小, 提高了通道壁面换热能力; 同时也可以看出, 随着肋高比的增大, 通道壁面平均努塞尔数比的增幅有所减小。通道的摩擦因数比随着肋高比的增大而增大, 且增幅也增大, 这是因为随着肋高比的增大, 肋片处主流的流通面积不断减小, 通道内流动阻力不断增大, 从而平均摩擦因数也相应增大。从图11中还可知:e/D为0.141时, 通道的综合性能因子最高; e/D为0.047时, 通道的综合性能因子最低; 而e/D为0.094和0.188时, 通道的综合性能因子相差很小。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 肋高比对通道内蒸汽流动和换热性能的影响Fig.11 Influence of e/D on flow and heat transfer performance of steam in channel

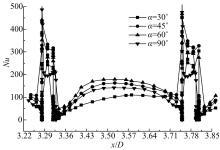
图12为不同肋角度时, 通道带肋壁面当地努塞尔数沿流向的分布曲线。从图12可以看出:在肋片之间区域, 壁面努塞尔数由大到小分别是肋角度为60° 、45° 、90° 和30° 的通道, 而在肋片区域, 壁面努塞尔数由大到小分别是肋角度为45° 、60° 、30° 和90° 的通道。因此, 在评价肋角度对带肋通道壁面换热性能的影响时, 只取肋片之间区域的平均努塞尔数比与取整个带肋壁面的平均努塞尔数比所得到的结果是有差异的。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 不同肋角度时通道带肋壁面当地努塞尔数分布Fig.12 Local Nu distribution at different rib angles on ribbed wall

图13为不同肋角度时, 通道带肋壁面平均努塞尔数比、摩擦因数比及综合性能因子分布曲线。从图13可以看出:通道摩擦因数比随着肋角度的增大而增大;

图13

Fig.13

	Figure Option ViewDownloadNew Window
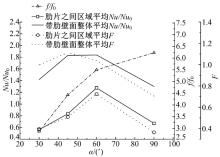	图13 肋角度对通道内蒸汽流动及换热性能的影响Fig.13 Influence of rib angles on flow and heat transfer performance of steam in channel

只取肋片之间区域的平均努塞尔数比时, 肋角度为60° 的肋通道壁面的换热性能和综合性能因子最好, 其次为肋角度为45° 、90° 的肋通道, 肋角度为30° 的肋通道最差。而取带肋壁面整体平均努塞尔数比时, 肋角度为45° 和60° 的肋通道壁面换热性能最好, 肋角度为30° 的肋通道的换热性能要好于90° 肋通道; 肋角度为45° 的肋通道的综合性能因子最高, 肋角度为30° 与60° 肋通道综合性能因子相差很小, 肋角度为90° 的肋通道综合性能因子最低。

厚壁带肋通道蒸汽冷却的传热关联式对于指导未来重型燃机涡轮叶片蒸汽冷却结构的设计具有重要意义。根据前文分析, Nu随着壁厚的增大而单调下降, 随着肋高比的增大而单调上升, 可以采用幂函数对Nu与壁厚和肋高比进行拟合; 而Nu随着肋角度的增大先增大后减小, 因此, 对于肋角度, 需要在使用幂函数拟合前找到其极值点, 经过测试, 可以采用有理分式对Nu和肋角度 α进行拟合(为与其他结构参数对应的Nu统一, 取整个带肋壁面的平均努塞尔数进行拟合), 其公式如下:

Nu(α)=a1+a2α1+a3α+a4α2(11)

式中: a1~a4为有理多项式的待求系数。

经过有理分式的非线性拟合, 得到式(12), 拟合曲线如图14所示, 拟合的残差在1× 10^-14量级。经过计算, 肋角度 α为53° 时, 通道壁面的Nu达到了峰值。

Nu(α)=33.9904+1.2649α1-0.02241α+0.000288α2(12)

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 Nu与肋角度拟合曲线Fig.14 Fitted curve of Nu and rib angles

因此, 本文假设Nu关于通道壁厚、肋高比和肋角度的公式如下:

Nu=b1Re0.8δb2(e/D)b3(|α-53|)b4(13)

式中: b1~b4为Nu关联式的待求系数。

基于研究的数据点, 采用多元线性回归方法拟合反映通道壁厚、肋高比和肋角度对厚壁带肋通道影响的传热特性关联式, 得到的传热关联式为:

Nu=0.5938Re0.8δ-0.0275(e/D)0.7176(|α-53|)-0.2173(14)

其适用范围为:0.1 mm≤ δ ≤ 4 mm; 0.047≤ e/D≤ 0.188; 30° ≤ α ≤ 90° 。

图15为Nu关联式拟合误差的分布图。由图可知:传热关联式的拟合误差在5%以内, 最大误差为-3.88%, 说明拟合的传热关联式可以准确地预测厚壁带肋通道的换热系数。

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 拟合误差分布Fig.15 Fitting error distribution