重载静压转台承载力与油垫温度场分布的关系

引用本文

刘志峰, 赵代红, 王语莫, 浑连明, 赵永胜, 董湘敏. 重载静压转台承载力与油垫温度场分布的关系[J].吉林大学学报（工学版）, 2018,48(3): 773-780
LIU Zhi-feng, ZHAO Dai-hong, WANG Yu-mo, HUN Lian-ming, ZHAO Yong-sheng, DONG Xiang-min. Relationship between bearing capacity of heavy machine hydrostatic rotary table and temperature field distribution of oil pad[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 773-780 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170152
Permissions

重载静压转台承载力与油垫温度场分布的关系

刘志峰¹, 赵代红¹, 王语莫¹, 浑连明¹, 赵永胜¹, 董湘敏²

1.北京工业大学先进制造技术北京市重点实验室,北京 100124

2.承德石油高等专科学校机械工程系,河北承德067000

作者简介:刘志峰(1973-),男,教授,博士生导师.研究方向:数字化设计与制造.E-mail:lzf@bjut.edu.cn

基金:国家自然科学基金项目(51575009); 国家科技重大专项项目(2013ZX04013-011); “京华人才”支持项目.

摘要

推导了极坐标下考虑离心力的雷诺方程,建立了以对流散热为主的极坐标下的能量方程,将雷诺方程与能量方程进行联立,利用有限差分法建立了不同转速下油垫温度分布与重载静压转台承载性能的变化关系。同时,在某5 m立车静压支承试验台进行测试试验和相关分析验证,证明了所建模型的正确性。结果表明:油膜温度随转台转速增大而升高;当转速达到40 r/min时温度迅速升高,承载力急剧下降。油垫封油边四周温度升高不同,速度大的一侧的温度升高更加明显,易产生局部高温。研究结果可为进一步分析静压转台的热补偿及结构设计优化提供理论依据和数据参考。

关键词: 机械设计; 温度场; 重型静压转台; 转速; 承载力

中图分类号:TG117.1 文献标志码:A 文章编号:1671-5497(2018)03-0773-08

Relationship between bearing capacity of heavy machine hydrostatic rotary table and temperature field distribution of oil pad

LIU Zhi-feng¹, ZHAO Dai-hong¹, WANG Yu-mo¹, HUN Lian-ming¹, ZHAO Yong-sheng¹, DONG Xiang-min²

1.Beijing Key Laboratory of Advanced Manufacturing Technology, Beijing University of Technology, Beijing 100124,China

2. Department of Mechanical Engineering,Chengde Petroleum College, Chengde 067000,China

Abstract

As temperature increases the viscosity of the heavy machine hydrostatic turntable oil film decreases, resulting in the decrease in the bearing capacity of the table. Therefore, temperature is an important factor affecting the speed and bearing capacity of the turntable. The Reynolds equation considering the centrifugal force and the convection dominated energy equations are simultaneously established in polar coordinates. Finite difference method is applied to establish the relationship between temperature distribution and bearing capacity of the hydrostatic turntable under different speed. The established model is verified in a 5 meter vertical lathe hydrostatic bearing test rig. The results show the oil temperature increases with the rotation speed of the table; when the speed reaches 40r/min, the temperature rises rapidly and the bearing capacity decreases sharply. The oil gasket seal edge temperature rise is different, in the high speed side the temperature rise is more obvious, resulting in local high temperature region. This study may provide reference for further analysis of thermal compensation and structural design optimization of hydrostatic turntable.

Keyword: mechanical design; temperature field; heavy machine hydrostatic rotary table; rotating speed; bearing capacity

文章图片

0 引言

静压转台相比与传统转台有许多优势, 最显著的特点是可以在很高的转速和较低的温度下保持较高的可靠性, 并且降低了对形位公差的要求。油腔中油膜工作性能的优劣直接影响到整个机床运行的可靠性、寿命和经济指标^[1]。随着技术的进步, 发热问题逐渐成为制约其性能和精度提升的关键因素。

国内、外学者在液体静压轴承热态性能研究方面做了很多工作, Sim等^[2]对一种轴颈可倾斜的气体轴承建立了三维热模型, 此模型不仅可以计算轴承套和转子的温度还可以计算气体薄膜的温度, 该模型采用了全局热平衡的方法并利用到了轴承套和转子的温度边界条件。André s等^[3]对比了用来估计动、静态波箔轴承负载能力的一维和二维温度有限元模型, 该模型顶箔的变形通过一个刚度矩阵和雷诺方程耦合在一起, 能很好地符合试验数据。刘志峰等^[4]建立了多油垫静压转台的多自由度动力学模型, 计算了静压转台在均载及偏载时的响应及静压转台的稳定时间和稳态油膜厚度。

关于滑动轴承的热弹流问题, Ezzat^[5]、Christensen^[6]和Rathish等^[7]利用数值分析的方法进行了研究。Kango等^[8]利用有限差分法分析了热弹流的各个参数对径向轴承性能的综合影响。李嶸等^[9]针对定量供油重载静压轴承, 提出了一种考虑速度和窜油影响且适合工程计算分析的油腔压强计算方法。Dai等^[10]利用Fluent软件分析了静压轴承的压力场, 综合分析了转速和供油压力对承载特性的影响。Lu等^[11]分析了水润滑陶瓷轴承的热特性, 并与其他材料轴承的最大工作温度做了对比。Li^[12]建立了重型数控机床矩形油垫油液的速度、压力和流量的数学模型, 并分析了其承载特性。Yadav等^[13]提出了一种提高静压推力轴承性能的新技术, 研究得到的表面纹理使摩擦功率随其他参数的提高而显著降低。Chen等^[14]计算了静压主轴的油液流动状态、热分布和主轴表面的对流交换系数, 并分析了热对油膜刚度的影响。Razzaque等^[15]基于NGT理论对静压止推轴承开槽的影响进行了研究, 结果表明适当的开槽设计可以提高承载力。衡凤琴等^[16]探讨了不同转速下, 因油膜的摩擦发热而导致的静压转台温度场及热变形场的变化规律。崔鹏威^[17]采用静压理论计算得到静压转台各油垫处的温度升高及静压转台温度分布情况, 分析了转速和承重对静压转台温升和黏度的影响规律, 得到静压转台在考虑温黏效应时的热特性变化情况。邵俊鹏等^[18]利用有限体积法, 模拟了扇形腔和圆形腔间隙流体的温度场, 探讨了在转速、腔深和有效承载面积相同时两种腔形的温度分布规律, 优化了油腔结构。于晓东等^[19]研究了环形腔多油垫静压推力轴承热变形与转速的关系, 结果表明, 随着旋转工作台转速的增大, 工作台和底座的热变形呈上升趋势, 转速越高热变形越大。

由于温度显著地改变润滑剂的黏度, 进而影响压力分布和承载能力。此外, 润滑表面由于温升而产生的热变形使间隙形状改变, 从而影响润滑性能。温度过高还可能引起润滑剂和表面材料失效, 通常取局部温度极限值为120~140 ℃^[20]。学者对静压轴承的温度分布研究得比较深入, 对于静压转台的研究主要集中在利用Fluent等软件仿真得到静压转台的温度分布情况, 并没有完善的理论指导依据。本文在外载荷一定的情况下, 以转台自重为基础, 从雷诺方程和能量方程出发, 忽略流体流动时的动能和势能变化, 利用有限差分法求解方程, 建立了不同转速下油垫的温度分布曲线, 分析了油垫的温度分布和承载性能随转速的变化规律。在5 m立车静压支承试验台进行了试验验证, 试验结果与理论计算结果吻合, 从而说明数值模拟的正确性和可行性。

1 温度模型

1.1 雷诺方程

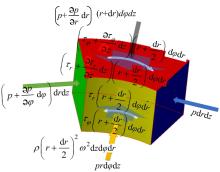
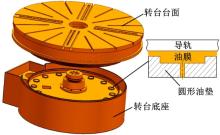静压转台及其圆形油垫结构示意图如图1所示, 在圆形油垫油膜上任取一微元体, 其受力如图2所示, 微元体在 $r$ 方向受到正压力 $pr d φ d z 、 (p + \frac{\partial p}{\partial r} d r) (r + d r) d φ d z,$ 离心力 $ρ {(r + \frac{d r}{2})}^{2} ω^{2} d z d φ d r$ 和切应力 $\begin{array}{l} (τ_{r} + \frac{\partial τ_{r}}{\partial z} d z) (r + \frac{d r}{2}) d φ d r 、 τ_{r} (r + \frac{d r}{2}) \times \\ d φ d r \end{array}$ 的作用; 在 $φ$ 方向受到正压力 $p d r d z 、 (p + \frac{\partial p}{\partial φ} d φ) d r d z$ 和切应力 $τ_{φ} (r + \frac{d r}{2}) d φ d r 、 (τ_{φ} + \frac{\partial τ_{φ}}{\partial z} d z) (r + \frac{d r}{2}) d φ d r$ 的作用。其中, $r 、 φ 和 z$ 分别为柱坐标系下的坐标参量; $τ_{φ}$ 和 $τ_{r}$ 分别为微元体在 $φ$ 方向和 $r$ 方向的切应力; $p$ 为油液压力; $ρ$ 为油液密度; $ω$ 为转台转速。

	Figure Option View Download New Window
	图1 静压转台及其圆形油垫结构示意图Fig.1 Schematic diagram of configuration of hydro-static rotary table and circular oil pad

	Figure Option View Download New Window
	图2 微元体受力Fig.2 Force distribution of infinitesimal body

根据微元体的受力情况可列出微元的力平衡方程, 根据 $r$ 方向受力平衡, 可得:

$\begin{array}{l} (p + \frac{\partial p}{\partial r} d r) (r + d r) d φ d z + τ_{r} (r + \frac{d r}{2}) d φ d r = \\ ρ {(r + \frac{d r}{2})}^{2} ω^{2} d z d φ d r + (τ_{r} + \frac{\partial τ_{r}}{\partial z} d z) (r + \frac{d r}{2}) \cdot \\ d φ d r + pr d φ d z (1) \end{array}$

根据 $φ$ 方向受力平衡, 可得:

$\begin{array}{l} p d r d z + (τ_{φ} + \frac{\partial τ_{φ}}{\partial z} d z) (r + \frac{d r}{2}) d φ d r = \\ (p + \frac{\partial p}{\partial φ} d φ) d r d z + τ_{φ} (r + \frac{d r}{2}) d φ d r (2) \end{array}$

本文认为润滑剂是牛顿流体, 流动为层流, 油液不可压缩, 根据牛顿黏性定律, 将 $τ_{r} = η \frac{\partial v_{r}}{\partial z} 、 τ_{φ} = η \frac{\partial v_{φ}}{\partial z}$ 代入式(2), 并略去高阶微小量可得:

$\{\begin{array}{l} rη \frac{\partial^{2} v_{φ}}{\partial z^{2}} = \frac{\partial p}{\partial φ} \\ rη \frac{\partial^{2} v_{r}}{\partial z^{2}} + ρ r^{2} ω^{2} = r \frac{\partial p}{\partial r} + p \end{array} (3)$

式中: $v_{r} 、 v_{φ}$ 分别为润滑膜中任意点油液沿 $r$ 和 $φ$ 方向的流速; $η$ 为动力黏度。

认为沿润滑膜厚度方向不计压力变化, 沿润滑膜厚度方向黏度数值不变, 所以将式(3)对 $z$ 进行二次积分并代入边界条件:当 $z = h 时, v_{φ} = V_{φ}; 当 z = 0$ 时, $v_{φ} = 0,$ 求得:

$v_{φ} = \frac{(- \frac{1}{2} h (h - z) \frac{\partial p}{\partial φ} + V_{φ} ηr) z}{hηr} (4)$

式中: $h$ 为油膜厚度; $V_{φ}$ 为与油膜接触的导轨下表面沿 $φ$ 方向的速度分量。

将 $ω = v_{φ} / r$ 代入式(4), 同样对 $z$ 进行二次积分并代入边界条件:当 $z = h$ 时, $v_{r} = V_{r}; 当 z = 0$ 时, $v_{r} = 0,$ 求得:

$\begin{array}{l} v_{r} = \frac{1}{η^{3} r^{3} h^{3}} \{z [\frac{1}{240} h^{2} ρ (h - z) \cdot (h^{4} + \\ h^{3} z) + h^{2} z^{2} - 4 h z^{3} + 2 z^{4} {(\frac{\partial p}{\partial φ})}^{2} - \\ \frac{1}{30} V_{φ} η (h - z) hrρ (h^{3} + z h^{2} + z^{2} h - \frac{3}{2} z^{3}) \frac{\partial p}{\partial φ} + \\ η^{2} r^{2} (- \frac{1}{2} h^{3} r \frac{\partial p}{\partial r} + \frac{1}{2} h^{2} rz \frac{\partial p}{\partial r} - \frac{1}{2} h^{3} p + \\ \frac{1}{2} h^{2} pz + \frac{1}{12} V_{φ}^{2} h^{3} ρ - \frac{1}{12} z^{3} ρ V_{φ}^{2} + V_{r} hrη)]\} (5) \end{array}$

式中: $V_{r}$ 为与油膜接触的导轨下表面沿 $r$ 方向的速度分量。

不可压缩流体运动的连续性方程为:

$\frac{\partial v_{r}}{\partial r} + \frac{v_{r}}{r} + \frac{1}{r} \frac{\partial v_{φ}}{\partial φ} + \frac{\partial v_{z}}{\partial z} = 0 (6)$

式中: $v_{z}$ 为润滑膜中任意点油液沿 $z$ 方向的流速。

将式(6)对 $z$ 积分, 交换微分次序, 化简可得:

$\begin{array}{l} \frac{1}{r} \frac{\partial}{\partial r} \int_{0}^{h} r v_{r} d z - V_{r} \frac{\partial h}{\partial r} + \frac{1}{r} \frac{\partial}{\partial φ} \int_{0}^{h} v_{φ} d z - \\ \frac{1}{r} V_{φ} \frac{\partial h}{\partial φ} + V_{z} = 0 (7) \end{array}$

式中: $V_{z}$ 为与油膜接触的导轨下表面沿 $z$ 方向的速度分量, 即当 $z = h 时 v_{z} = V_{z} 。$

将式(4)(5)代入式(7), 并略去 $h$ 的高次项, 则可得到考虑离心力作用的极坐标雷诺方程为:

$\begin{array}{l} \frac{1}{r} \frac{\partial}{\partial r} (\frac{h^{3} {V_{φ}}^{2} ρ}{40 η} - \frac{h^{3} r \frac{\partial p}{\partial r}}{12 η} - \frac{h^{3} p}{12 η} + \frac{hr V_{r}}{2}) + \\ \frac{1}{r} \frac{\partial}{\partial φ} (\frac{6 h V_{φ} ηr - h^{3} \frac{\partial p}{\partial φ}}{12 ηr}) - \frac{V_{φ}}{r} \frac{\partial h}{\partial φ} + V_{z} = 0 \\ (8) \end{array}$

1.2 能量方程

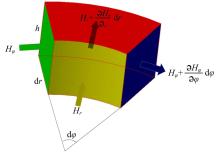
对于流体润滑, 可以忽略流体流动时的动能和势能变化, 这样, 流体的能量变化仅是温度的函数。假设流动处于稳定状态, 因而所有的变量均不随时间变化。本文计算时, 以对流散热为主而忽略膜厚方向的热传导, 所以 $\partial T / \partial z = 0$ , 润滑膜温度 $T$ 只是 $r$ 和 $φ$ 的函数。

分析流体在流动中热能的变化, 如图3所示, 取夹角为 $d φ,$ 径向长度为 $d r,$ 高度为 $h$ 的微元体进行分析。设 $q_{φ}$ 和 $q_{r}$ 分别代表微元体周向和径向的容积流量, $c$ 为油液比热容, 那么流入微元体的热流量应为 $H_{r} = q_{r} Tρc$ 和 $H_{φ} = q_{φ} Tρc,$ 若取 $d φ = d r = 1,$ 则流入微元体的热量总和为:

$\begin{array}{l} H_{r} + H_{φ} - (H_{r} + \frac{\partial H_{r}}{\partial r}) - (H_{φ} + \frac{\partial H_{φ}}{\partial φ}) = \\ - \frac{\partial H_{r}}{\partial r} - \frac{\partial H_{φ}}{\partial φ} (9) \end{array}$

	Figure Option View Download New Window
	图3 热流动Fig.3 Thermal flow

用 $W$ 表示流体在微元体中所做的机械功, 将 $H_{r} = q_{r} Tρc$ 和 $H_{φ} = q_{φ} Tρc$ 代入式(9), 那么根据能量守恒原理可以得到如下关系式:

$\frac{\partial (q_{r} T)}{\partial r} + \frac{\partial (q_{φ} T)}{\partial φ} = - \frac{W}{ρc} (10)$

由流量连续条件可知:

$\frac{\partial q_{r}}{\partial r} + \frac{\partial q_{φ}}{\partial φ} = 0 (11)$

则有:

$q_{r} \frac{\partial T}{\partial r} + q_{φ} \frac{\partial T}{\partial φ} = - \frac{W}{ρc} (12)$

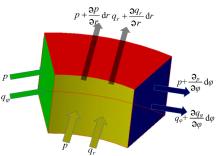
流体在微元体中所做的机械功包括流动功和摩擦功两部分, 如图4所示。

	Figure Option View Download New Window
	图4 流体流动Fig.4 Fluid flow

$r$ 方向的流动功为:

$(p + \frac{\partial p}{\partial r} d r) (q_{r} + \frac{\partial q_{r}}{\partial r} d r) - p q_{r}$

取 $d r = 1,$ 略去高阶微量, 则沿 $r$ 方向流动功为:

$q_{r} \frac{\partial p}{\partial r} + p \frac{\partial q_{r}}{\partial r}$

同理可得沿 $φ$ 方向的流动功, 则微元体所做的总流动功为:

$q_{r} \frac{\partial p}{\partial r} + q_{φ} \frac{\partial p}{\partial φ} + p (\frac{\partial q_{r}}{\partial r} + \frac{\partial q_{φ}}{\partial φ})$

又因为 $\frac{\partial q_{r}}{\partial r} + \frac{\partial q_{φ}}{\partial φ} = 0,$ 因而总流动功变为:

$q_{r} \frac{\partial p}{\partial r} + q_{φ} \frac{\partial p}{\partial φ}$

略去 $h$ 高次项, 可得径向流量为:

$q_{r} = \int_{0}^{h} v_{r} r d z = \frac{h^{3} ρ {V_{φ}}^{2}}{40 η} - \frac{h^{3} r}{12 η} \frac{\partial p}{\partial r} - \frac{h^{3} p}{12 η} + \frac{1}{2} V_{r} hr (13)$

同理, 可得周向流量为:

$q_{φ} = \int_{0}^{h} v_{φ} d z = - \frac{h^{3}}{12 ηr} \frac{\partial p}{\partial φ} + \frac{1}{2} h V_{φ} (14)$

静压转台油膜下表面速度为0, 故只需计算上表面摩擦力所做的功, $r$ 方向微元体上表面摩擦力为:

$f_{r} = η {\frac{\partial v_{r}}{\partial z}|}_{z = h} r d r d φ (15)$

由于取 $d φ = d r = 1,$ 故 $f_{r} = η {\frac{\partial v_{r}}{\partial z}|}_{z = h} r,$ 代入式(5)并略去 $h$ 高次项可得:

$\begin{array}{l} f_{r} = \frac{h^{3} V_{φ} ρ \frac{\partial p}{\partial φ}}{20 ηr} + \frac{1}{2} rh \frac{\partial p}{\partial r} + \frac{1}{2} hp - \\ \frac{1}{4} hρ {V_{φ}}^{2} + \frac{rη V_{r}}{h} (16) \end{array}$

微元体中 $r$ 方向摩擦力做功为:

$\begin{array}{l} - f_{r} V_{r} = - V_{r} [h^{3} V_{φ} ρ \frac{\partial p}{\partial φ} {(20 ηr)}^{- 1} + \frac{1}{2} rh \frac{\partial p}{\partial r} + \\ \frac{1}{2} hp - \frac{1}{4} hρ {V_{φ}}^{2} + \frac{rη V_{r}}{h}] (17) \end{array}$

同理微元体中 $φ$ 方向摩擦力做功为:

$- f_{φ} V_{φ} = - V_{φ} (\frac{1}{2} \frac{\partial p}{\partial φ} h + \frac{ηr V_{φ}}{h}) (18)$

微元体所消耗的总功 $W$ 为:

$W = - f_{φ} V_{φ} - f_{r} V_{r} + q_{r} \frac{\partial p}{\partial r} + q_{φ} \frac{\partial p}{\partial φ} (19)$

将式(14)(15)(17)(18)代入式(19)得:

$\begin{array}{l} W = - \frac{h^{3}}{12 rη} {(\frac{\partial p}{\partial φ})}^{2} - \frac{V_{φ} ρ V_{r} h^{3}}{20 rη} \frac{\partial p}{\partial φ} - \frac{r h^{3}}{12 η} {(\frac{\partial p}{\partial r})}^{2} + \\ \frac{ρ {V_{φ}}^{2} h^{3}}{40 η} \frac{\partial p}{\partial r} - \frac{p h^{3}}{12 η} \frac{\partial p}{\partial r} - \frac{1}{2} V_{r} ph + \\ \frac{1}{4} V_{r} {V_{φ}}^{2} ρh - \frac{rη {V_{r}}^{2}}{h} - \frac{rη {V_{φ}}^{2}}{h} (20) \end{array}$

再将式(12)代入式(20), 经整理求得静压转台油膜的能量方程为:

$\begin{array}{l} q_{r} \frac{\partial T}{\partial r} + q_{φ} \frac{\partial T}{\partial φ} = \frac{h^{3}}{12 ρcrη} {(\frac{\partial p}{\partial φ})}^{2} + \frac{V_{φ} V_{r} h^{3}}{20 crη} \frac{\partial p}{\partial φ} + \\ \frac{r h^{3}}{12 ρcη} {(\frac{\partial p}{\partial r})}^{2} - \frac{{V_{φ}}^{2} h^{3}}{40 cη} \frac{\partial p}{\partial r} + \frac{p h^{3}}{12 ρcη} \frac{\partial p}{\partial r} + \\ \frac{V_{r} ph}{2 ρc} - \frac{V_{r} {V_{φ}}^{2} h}{4 c} + \frac{rη {V_{r}}^{2}}{hρc} + \frac{rη {V_{φ}}^{2}}{hρc} \\ (21) \end{array}$

1.3 数值求解

表1为试验静压转台油垫的几何参数和油液参数。要求解温度场, 必须先求得压力场, 而压力又受到温度的影响, 所以考虑热效应的静压转台承载力必须对雷诺方程与能量方程联立求解。

表1 静压转台几何参数和油液参数 Table 1 Parameters of hydrostatic rotary table and oil

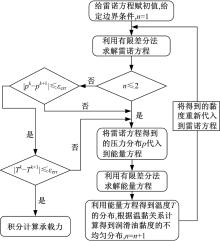
利用有限差分法对雷诺方程(8)和能量方程(21)进行联立迭代求解, 直到压强分布误差满足精度要求。最后通过积分计算油垫的承载力。给定雷诺方程的边界条件:在油腔内 $\bar{p} = 1,$ 在四周边缘上 $\bar{p} = 0; V_{z} = 0 。$ 无量纲承载力 $\bar{F}$ 和无量纲流量 $\bar{Q}$ 的计算公式分别为:

$\begin{array}{l} \bar{F} = π R_{0}^{2} + \int_{0}^{2} \int_{R_{0}}^{R_{1}} \bar{p} r d r d φ (22) \\ \bar{Q} = \int_{0}^{2} \int_{0}^{h} {\bar{q}}_{r} |_{_{r = R_{1}}} r d r d φ (23) \end{array}$

承载力F和流量Q的计算公式为:

$\{\begin{array}{l} F = \bar{F} π R_{0}^{2} p_{0} \\ Q = \bar{Q} H_{0}^{3} p_{0} / η_{0} \end{array} (24)$

式中: $p_{0}$ 为供油压力。

由式(24)求得:

$\{\begin{array}{l} p_{0} = Q η_{0} / \bar{Q} H_{0}^{3} \\ F = \bar{F} π R_{0}^{2} Q η_{0} / H_{0}^{3} \bar{Q} \end{array} (25)$

将式(22)代入式(25)得到承载力计算公式为:

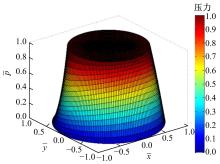
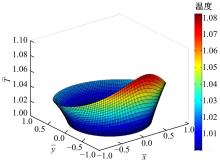
$F = (π R_{0}^{2} + \int_{0}^{2} \int_{R_{0}}^{R_{1}} \bar{p} r d r d φ) π R_{0}^{2} Q η_{0} / H_{0}^{3} \bar{Q} (26)$

之后, 改变静压转台转速得到不同转速下的油垫压力分布、温度分布和承载力。具体计算流程如图5所示。为了对比引入温黏关系对承载力的影响, 分别计算考虑温升的承载力和不考虑温升的承载力。图6和图7为油垫封油边无量纲压力和温度分布图, 封油边的温度沿直径方向向外逐渐升高, 可以看出, 承载力分布高的地方温升也大。

	Figure Option View Download New Window
	图5 温压耦合求解流程图Fig.5 Flow chart for coupled solution of pressure-thermal

	Figure Option View Download New Window
	图6 封油边无量纲压力分布图Fig.6 Nephogram of dimensionless pressure distribution of oil seal edge

	Figure Option View Download New Window
	图7 封油边无量纲温度分布图Fig.7 Nephogram of dimensionless temperature distribution of oil seal edge

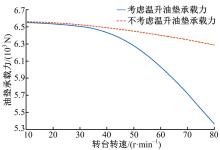
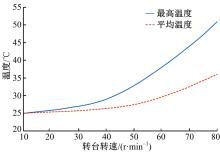
不考虑温升时, 静压转台转速由10 r/min增加到80 r/min, 油膜承载力随转速的变化如图8中虚线所示, 考虑温升的承载力与转速关系如图8中实线所示。计算结果表明, 随着转速的增大油垫承载力呈下降趋势, 但考虑温升之后承载力下降得更多, 且转速越高这种差异越明显。这是因为转速越高发热量越大, 温度升高越大, 根据温黏关系式可知油液黏度降低导致承载力下降。当转速达到80 r/min时, 油垫平均温度升高了11 ℃, 最高温度变化了25.8 ℃, 由于温升导致承载能力下降了18.1%, 这说明温升对油膜承载能力有较大影响。由图9可以看出:虽然油膜平均温度变化不是很大, 但是最高温度对转速很敏感, 随转速提高温度上升剧烈。

	Figure Option View Download New Window
	图8 不同转速下油垫的承载力分布Fig.8 Bearing capacity of oil pad distribution in different rotating speed

	Figure Option View Download New Window
	图9 不同转速下的油膜温度分布Fig.9 Oil film temperature distribution in different rotating speed

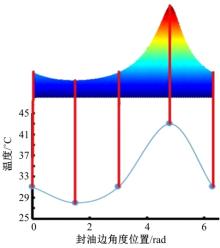图10为静压转台转速为60 r/min时分别在 $φ = 0 、 φ = π / 2 、 φ = π 、 φ = 3 π / 2$ 和 $φ = 2 π$ 处的最高温度分布。从图10中可以看出:油垫温度分布沿周向大致成正弦函数形状,

	Figure Option View Download New Window
	图10 转速为60 r/min时油膜最高温度沿油垫周向分布Fig.10 Highest temperature of oil film along circumferential distribution under the speed of 60 r/min

这是由于油垫的中心与静压转台旋转中心不重合, 从而导致油垫油液的速度分布沿封油边轴向大致成正弦函数。具体的温度分布形状还与静压转台中心到油垫中心的距离、油垫半径和转速有关。

2 试验

2.1 试验装置

试验采用重型数控机床静压技术研发平台中的5 m立车静压支承试验台。转台整体内部结构和试验传感器布置位置如图11所示, 编号①~⑧分别是8个PT100温度传感器, 用来测量流出油垫封油边的油液温度。

	Figure Option View Download New Window
	图11 温度传感器布置位置Fig.11 Arrangement of temperature sensors

2.2 试验步骤

Step1 空载、静止, 在1 L/min供油状态下记录各电涡流传感器示数和各温度传感器示数。

Step2 将静压转台转速设置为60 r/min, 连续记录各电涡流传感器示数和各温度传感器示数, 直到温度传感器示数在连续2 min不再出现变化。

Step3 静压转台停止转动, 停止供油, 待油液自然冷却。

Step4 重复Step2和Step3三次。

2.3 试验结果

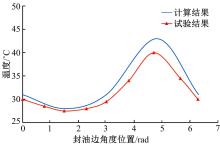
试验数据结果如表2所示, 与图10的计算结果进行对比, 结果如图12所示。可以看出, 低温时计算结果与试验结果较为接近, 最小误差为1.91%; 高温时误差较大, 最大误差为7.15%。整体数值计算结果与试验结果吻合较好, 变化趋于一致, 试验结果的温升要略低于数值计算结果。

表2 转速为60 r/min时的油垫温升分布试验数据 Table 2 Experimental data of temperature rise distribution of oil pad under speed of 60 r/min ℃

	Figure Option View Download New Window
	图12 计算结果与试验结果对比Fig.12 Comparison between calculated results and experimental results

2.4 误差分析

(1)由于试验条件所限, 传感器只能布置在油垫外间接测量封油边最外沿的温度, 油液流出油垫之后, 接触空气后流到静压转台基座, 这个过程中存在一定的能量损失。

(2)为了简化计算, 本文数值计算没有考虑沿油膜厚度方向通过固体表面的传导散热(油液在高速状态下(Peclet数≤ 0.1)以对流散热为主^[19]), 也导致温升计算结果偏高。

3 结束语

通过联立雷诺方程与能量方程, 建立了极坐标下考虑离心力的温度场数学模型。利用有限差分法求解出油膜温度场的分布, 给出了温升随转速的变化规律。考虑温升之后的油膜承载力变化很大, 尤其在高转速下, 承载力比不考虑温度升高时的计算结果下降约18.1%。当转速为80 r/min时, 油垫平均温度升高了11 ℃, 最高温度变化了25.8 ℃。通过以上研究可以得出:油膜温度随转速提高上升剧烈, 尤其是在大直径高速重型静压转台上这种效果更加明显, 油膜局部温度过高易导致油液失效及产生热变形。静压转台与油垫的相对尺寸也会影响油膜温度的分布情况。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	钟洪, 张冠坤. 液体静压动静压轴承设计使用手册[M]. 北京: 电子工业出版社, 2007. [本文引用:1]
[2]	Sim K, Kim D. Thermohydrodynamic analysis of compliant flexure pivot tilting pad gas bearings[J]. Journal of Engineering for Gas Turbines and Power, 2008, 130(3): 032502. [本文引用:1]
[3]	Andrés S L, Kim T H. Analysis of gas foil bearings integrating FE top foilmodels[J]. Tribology International, 2009, 42(1): 111-120. [本文引用:1]
[4]	刘志峰, 湛承鹏, 赵永胜. 定量式静压转台动态特性建模与影响因素分析[J]. 机械工程学报, 2015, 51(19): 75-83. Liu Zhi-feng, Zhan Cheng-peng, Zhao Yong-sheng. Modeling and analysis of the dynamic behaviors of a quantitative type hydrostatic rotary table[J]. Journal of Mechanical Engineering, 2015, 51(19): 75-83. [本文引用:1]
[5]	Ezzat H A, Rohde S M. A study of the thermohydrodynamic performance of finite slider bearings[J]. Journal of Tribology-Transactions of the ASME, 1973, 95(3): 298-307. [本文引用:1]
[6]	Christensen H. Stochastic models for hydrodynamic lubrication of rough surfaces[J]. Proceedings of Institute of Mechanical Engineering, 1969, 184: 1013-1022. [本文引用:1]
[7]	Rathish B V, Rao P S, Sinha P. Stream line upwind Petrov-Galerkin finite element analysis of thermal effects on load carrying capacity in slider bearings[J]. Numerical Heat Transfer Applications, 2000, 38(3): 305-328. [本文引用:1]
[8]	Kango S, Sharma R K, Pand ey R K. Thermal analysis of microtextured journal bearing using non-Newtonian rheology of lubricant and JFO boundary conditions[J]. Tribology International, 2014, 69: 19-29. [本文引用:1]
[9]	李嶸, 桂林, 孟曙光. 考虑速度和窜油影响的重载静压轴承油腔压力解析研究[J]. 制造技术与机床, 2016(7): 62-66. Li Rong, Gui Lin, Meng Shu-guang. Analytical research on oil cavity pressure of heavy-duty hydrostatic bearing considering the effects of speed and channeling oil[J]. Manufacturing Technology & Machine Tool, 2016(7): 62-66. [本文引用:1]
[10]	Dai Hui-liang, Yao Li-juan, Peng Jin-li. Carrying capacity study of liquid hybrid bearing based on fluent[J]. Hydromechatronics Engineering, 2016, 44(12): 110-115. [本文引用:1]
[11]	Lu Dun, Liu Ke-jia, Zhao Wan-hua. Thermal characteristics of water-lubricated ceramic hydrostatic hydrodynamic hybrid bearings[J]. Tribology Letters, 2016, 63(2): 1-10. [本文引用:1]
[12]	Li Xi-bing. Theoretical research on mechanical property of rectangular oil pad in hydrostatic thrust bearing based on constant flow[J]. Industrial Lubrication and Tribology, 2016, 68(3): 392-403. [本文引用:1]
[13]	Yadav S K, Sharma S C. Performance of hydrostatic textured thrust bearing with supply holes operating with non-Newtonian lubricant[J]. Tribology Transactions, 2016, 59(3): 408-420. [本文引用:1]
[14]	Chen Dong-ju, Fan Jin-wei, Li Hai-yong. Thermal influence of the couette flow in a hydrostatic spindle on the machining precision[J]. Mechanical Engineering, 2013, 26(3): 427-436. [本文引用:1]
[15]	Razzaque M M, Hossain M Z. Effects of grooving in a hydrostatic circular step thrust bearing with porous facing[J]. Journal of Tribology-Transactions of the ASME, 2015, 137(3): 031703. [本文引用:1]
[16]	衡凤琴, 黄智, 陈学尚. 数控立车静压转台油膜温度场仿真分析及优化[J]. 机械科学与技术, 2015, 34(11): 1733-1737. Heng Feng-qin, Huang Zhi, Chen Xue-shang. Simulating and optimizing temperature field of oil film for CNC vertical lathe hydrostatic rotary table[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(11): 1733-1737. [本文引用:1]
[17]	崔鹏威. 重型静压转台动态误差及热变形分析研究[D]. 北京: 北京工业大学机械工程与应用电子技术学院, 2014. Cui Peng-wei. The research of the dynamic error and thermal deformation analysis on heavy duty hydrostatic rotary table[D]. Beijing: College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, 2014. [本文引用:1]
[18]	邵俊鹏, 张艳芹, 于晓东. 重型静压轴承扇形腔和圆形腔温度场数值模拟与分析[J]. 水动力学研究与进展, 2009, 24(1): 119-124. Shao Jun-peng, Zhang Yan-qin, Yu Xiao-dong. Numerical simulation analysis of sector and circular oil recess temperature field of heavy hydrostatic[J]. Journal of Hydrodynamics, 2009, 24(1): 119-124. [本文引用:1]
[19]	于晓东, 付旭, 刘丹, 等. 环形腔多油垫静压推力轴承热变形[J]. 吉林大学学报: 工学版, 2015, 45(2): 460-465. Yu Xiao-dong, Fu Xu, Liu Dan, et al. Thermal deformation of annular recess multi-pad hydrostatic thrust bearing[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(2): 460-465. [本文引用:2]
[20]	温诗铸. 摩擦学原理[M]. 北京: 清华大学出版社, 2012. [本文引用:1]

2007

0.0

... 油腔中油膜工作性能的优劣直接影响到整个机床运行的可靠性、寿命和经济指标^[1] ...

2008

0.0

... 国内、外学者在液体静压轴承热态性能研究方面做了很多工作,Sim等^[2]对一种轴颈可倾斜的气体轴承建立了三维热模型,此模型不仅可以计算轴承套和转子的温度还可以计算气体薄膜的温度,该模型采用了全局热平衡的方法并利用到了轴承套和转子的温度边界条件 ...

2009

0.0

... s等^[3]对比了用来估计动、静态波箔轴承负载能力的一维和二维温度有限元模型,该模型顶箔的变形通过一个刚度矩阵和雷诺方程耦合在一起,能很好地符合试验数据 ...

2015

0.0

. 2015, 51(19):75-83 DOI:doi:10.3901/JME.2015.19.075

Modeling and analysis of the dynamic behaviors of a quantitative type hydrostatic rotary table

定量式静压转台动态特性建模与影响因素分析

Liu Zhi-feng , Zhan Cheng-peng , Zhao Yong-sheng

刘志峰, 湛承鹏, 赵永胜

摘　要：静压转台的动力学性能对转台的综合性能有较大影响,所以对转台在动载作用下响应的深入研究对于转台优化设计及提升转台的综合性能有重要作用。根据Christensen的模型计算考虑表面粗糙度的情况下静压转台支承油垫及预压油垫的非线性承载力。建立多油垫转台的多自由度动力学模型,应用龙哥库塔法计算转台在均载及偏载时转台的响应及转台的稳定时间和稳态油膜厚度,分析表面粗糙度、转台初始油膜厚度、转台支承及预压油垫进油流量、转台转动对转台动态特性的影响。结果表明偏载使得转台的动态性能下降并使转台的某些支承油垫油膜厚度出现较大幅度降低。较小的油膜初始厚度和较大的流量可以提升转台的动态性能,而表面粗糙度等因素对于转台的动态特性也有比较明显的影响其中周向粗糙度倾向与提高转台性能而径向粗糙度则倾向于降低转台性能。所建的模型及分析结论将为转台的优化设计及转台综合性能的提升提供理论基础。

... 刘志峰等^[4]建立了多油垫静压转台的多自由度动力学模型,计算了静压转台在均载及偏载时的响应及静压转台的稳定时间和稳态油膜厚度 ...

1973

0.0

... 关于滑动轴承的热弹流问题,Ezzat^[5]、Christensen^[6]和Rathish等^[7]利用数值分析的方法进行了研究 ...

1969

0.0

... 关于滑动轴承的热弹流问题,Ezzat^[5]、Christensen^[6]和Rathish等^[7]利用数值分析的方法进行了研究 ...

2000

0.0

... 关于滑动轴承的热弹流问题,Ezzat^[5]、Christensen^[6]和Rathish等^[7]利用数值分析的方法进行了研究 ...

2014

0.0

... Kango等^[8]利用有限差分法分析了热弹流的各个参数对径向轴承性能的综合影响 ...

2016

0.0

. 2016, (7):62-66

Analytical research on oil cavity pressure of heavy-duty hydrostatic bearing considering the effects of speed and channeling oil

考虑速度和窜油影响的重载静压轴承油腔压力解析研究

Li Rong , Gui Lin , Meng Shu-guang

李嶸, 桂林, 孟曙光

摘　要：静压主轴高速旋转时,无回油槽静压轴承油腔之间的窜油会随速度增高而加剧,从而导致各油腔压力显著变化。传统经验计算方法由于忽略了窜油影响导致分析结果偏离实际工况,而采用三维流场仿真技术又存在计算效率低不适合工程上计算分析需要的缺点。针对定量供油重载静压轴承,提出了一种考虑速度和窜油影响且适合工程计算分析的油腔压强计算方法。利用所设计并搭建的数控落地铣镗床FB320静压轴承实验台,通过CFD油膜流场数值计算和实验测试对比研究,证实了所提出的解析方法的有效性。

... 李嶸等^[9]针对定量供油重载静压轴承,提出了一种考虑速度和窜油影响且适合工程计算分析的油腔压强计算方法 ...

2016

0.0

... Dai等^[10]利用Fluent软件分析了静压轴承的压力场,综合分析了转速和供油压力对承载特性的影响 ...

2016

0.0

... Lu等^[11]分析了水润滑陶瓷轴承的热特性,并与其他材料轴承的最大工作温度做了对比 ...

2016

0.0

... Li^[12]建立了重型数控机床矩形油垫油液的速度、压力和流量的数学模型,并分析了其承载特性 ...

2016

0.0

... Yadav等^[13]提出了一种提高静压推力轴承性能的新技术,研究得到的表面纹理使摩擦功率随其他参数的提高而显著降低 ...

2013

0.0

... Chen等^[14]计算了静压主轴的油液流动状态、热分布和主轴表面的对流交换系数,并分析了热对油膜刚度的影响 ...

2015

0.0

... Razzaque等^[15]基于NGT理论对静压止推轴承开槽的影响进行了研究,结果表明适当的开槽设计可以提高承载力 ...

2015

0.0

. 2015, 34(11):1733-1737

Simulating and optimizing temperature field of oil film for CNC vertical lathe hydrostatic rotary table

数控立车静压转台油膜温度场仿真分析及优化

Heng Feng-qin , Huang Zhi , Chen Xue-shang

衡凤琴, 黄智, 陈学尚

... 衡凤琴等^[16]探讨了不同转速下,因油膜的摩擦发热而导致的静压转台温度场及热变形场的变化规律 ...

2014

0.0

. 2014, :-

The research of the dynamic error and thermal deformation analysis on heavy duty hydrostatic rotary table

重型静压转台动态误差及热变形分析研究

Cui Peng-wei

崔鹏威

重型机床是装备制造业的重要基础与关键装备，主要用于大型、重型零部件加工。由于重型机床结构件与关键功能部件超大、超重的特点，其运动部件之间广泛采用静压技术。静压支承具有承载力高、刚度大、摩擦副间无磨损、油膜抗振性好、可克服爬行现象和运转平稳等一系列优点。重型静压转台是重型机床关键功能部件之一，主要用于承载大型加工工件，实现回转加工并可配合其他轴系运动实现五轴加工。因此，重型静压转台的性能优劣对重型机床加工精度起着至关重要的作用。本论文得到国家科技重大专项项目高档数控机床数字化设计关键技术与工具集研发及典型产品应用(项目编号2012ZX04010-011)的大力资助，主要研究的是重型机床静压转台轮廓误差对转台运动误差的影响、转台动态特性影响规律以及热特性的分析，并形成了一套静压转台动静热特性分析系统。为了探究各因素对静压转台精度和承载能力的影响规律，本文分别从转台运动误差、动态特性和热特性方面对静压转台进行了分析。首先以静压理论和有限元法为基础，根据重型静压转台的结构特点和工作情况，提出一种考虑导轨表面轮廓误差的运动误差分析方法，采用该方法分析了转台在不同位置处的平衡状态并求得相应的轴向运动误差、俯仰角和倾斜角误差，并分析了在内外圈导轨轮廓误差的共同作用下波长比对转台运动误差的影响规律以及不同轮廓误差分量对运动误差的影响，采用该方法对实验所测得的导轨轮廓模型进行了分析，得到了其运动误差大小，为提高转台实际运动误差提供了理论支撑。然后采用有限元法以线性弹簧等效静压油膜，对静压转台约束下的固有模态和谐响应特性进行了分析，并对比分析了不同工况下的固有频率变化，分析了承载重量、支承方式及支承刚度对静压转台动态特性的影响。接着采用静压理论计算得到了静压转台各轴承处的温升量及转台温度分布情况，分析了转速和承重对转台温升和粘度的影响规律，并分析了转台的热变形情况，得到转台在考虑温粘效应时的热特性变化情况。最后在前面分析工作的基础上，以ANSYS软件为平台，开发了静压转台同类结构件的动、静、热特性分析系统，大大的提高了分析的效率。

... 崔鹏威^[17]采用静压理论计算得到静压转台各油垫处的温度升高及静压转台温度分布情况,分析了转速和承重对静压转台温升和黏度的影响规律,得到静压转台在考虑温黏效应时的热特性变化情况 ...

2009

0.0

. 2009, 24(1):119-124

Numerical simulation analysis of sector and circular oil recess temperature field of heavy hydrostatic

重型静压轴承扇形腔和圆形腔温度场数值模拟与分析

Shao Jun-peng , Zhang Yan-qin , Yu Xiao-dong

邵俊鹏, 张艳芹, 于晓东

... 邵俊鹏等^[18]利用有限体积法,模拟了扇形腔和圆形腔间隙流体的温度场,探讨了在转速、腔深和有效承载面积相同时两种腔形的温度分布规律,优化了油腔结构 ...

2015

0.0

. 2015, 45(2):460-465

Thermal deformation of annular recess multi-pad hydrostatic thrust bearing

环形腔多油垫静压推力轴承热变形

Yu Xiao-dong , Fu Xu , Liu Dan

于晓东, 付旭, 刘丹

... 于晓东等^[19]研究了环形腔多油垫静压推力轴承热变形与转速的关系,结果表明,随着旋转工作台转速的增大,工作台和底座的热变形呈上升趋势,转速越高热变形越大 ...

... 1)以对流散热为主^[19]),也导致温升计算结果偏高 ...

2012

0.0

... 温度过高还可能引起润滑剂和表面材料失效,通常取局部温度极限值为120~140 ℃^[20] ...