基于相似理论的三跨桥梁磁流变隔振

引用本文

李锐, 张路阳, 刘琳, 武粤元, 陈世嵬. 基于相似理论的三跨桥梁磁流变隔振[J].吉林大学学报（工学版）, 2018,48(3): 787-795
LI Rui, ZHANG Lu-yang, LIU Lin, WU Yue-yuan, CHEN Shi-wei. Magneto-rheological vibration isolation for three-span bridge based on similarity theory[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 787-795 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170222
Permissions

基于相似理论的三跨桥梁磁流变隔振

李锐¹, 张路阳¹, 刘琳¹, 武粤元¹, 陈世嵬²

1.重庆邮电大学汽车电子与嵌入式系统工程研究中心,重庆 400065

2.重庆科技学院数理学院,重庆 401331

通讯作者：陈世嵬(1986-),男,副教授,博士.研究方向:振动控制与智能材料.E-mail:foranother@qq.com

作者简介:李锐(1975-),男,教授,博士.研究方向:智能检测技术与智能结构系统.E-mail:lirui_cqu@163.com

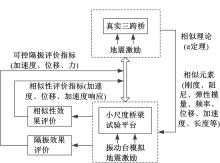
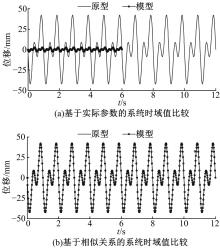
基金:重庆市杰出青年基金项目(cstc2014jcyjjq40004); 国家自然科学基金项目(11372366,11502038); 重庆市巴渝学者特聘教授项目.

摘要

采用无量纲相似分析法,计算出基于磁流变支座的三跨桥梁与小尺度试验台架的动力学关系,并以该关系为基础来指导试验台架模型的设计。运用Matlab分别对两系统进行动力学理论计算,仿真与试验结果表明:桥梁原型与模拟模型的加速度、位移等具有较好的相似性。进一步根据模型参数,搭建小尺度试验台架,试验结果与理论值基本吻合,桥面振动加速度峰值最大减小42%,位移峰值最大减小36%。表明采用相似理论进行模型试验研究能够揭示出桥梁可控隔振原型的主要隔振性能。

关键词: 机械设计; 桥梁; 无量纲分析; 磁流变支座; 隔振

中图分类号:TH113 文献标志码:A 文章编号:1671-5497(2018)03-0787-09

Magneto-rheological vibration isolation for three-span bridge based on similarity theory

LI Rui¹, ZHANG Lu-yang¹, LIU Lin¹, WU Yue-yuan¹, CHEN Shi-wei²

1.Engineering Research Center of Automotive Electronics and Embedded System, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

2.Academe Math and Physical,Chongqing University of Science and Technology, Chongqing 401331, China

Abstract

The dimensionless similarity analysis method is adopted to calculate the dynamic similarity relationship between a three-span bridge and a small-scale test bench based on Magneto-rheological Bearing (MRB). On the basis of the relationship, the test bench model s designed. Dynamics of the two systems are calculated by Matlab respectively. Simulation results show that the acceleration, displacement of the prototype and similar models have good similarity. Further, according to the model parameters, a small-scale test bench is built, and the experimental results are in good agreement with the theoretical results. The acceleration peak and displacement peak of the bridge deck can be reduced by 42% and 36%, respectively. Therefore, the model experimental study based on similarity theory can reveal the vibration isolation performance of the controllable prototype.

Keyword: mechanical design; bridge; dimensionless analysis; magneto-rheological elastomers bearing; vibration isolation

文章图片

0 引言

通过增加结构强度或采用被动支承(支座)来提高系统的抗振能力, 是桥梁等机械系统隔减振设计中的常用手段^[1]。但是, 被动支承(支座)在各种大的突发振动冲击载荷作用下, 缺乏智能调节横向刚度/强度来抵制剪切破坏力和过度移位的能力, 也难以通过增加阻尼来耗散瞬间有害能量, 其隔振、抗害能力不足^[2], 成为结构安全体系中最薄弱的环节。

目前, 有将磁流变阻尼器作为桥梁拉索附加减振装置的报道^[3], 但未从根本上考虑桥的墩-梁结构隔振问题。磁流变弹性体(Magneto-rheological elastomers, MRE)由磁性颗粒(如羰基铁粉)和聚合介质(如橡胶)等材料复合制成^[4], 在磁场作用下其刚度阻尼特性可控, 且具有响应快、可逆性好、可控能力强、稳定性好等优点^[5], 已成为结构抗震减灾领域研究的新热点, 如有学者研究了基于MRE支座的房屋建筑结构隔振技术, 为磁流变支座用于大型路桥建筑结构抗震探索了新方向^[6]。但是, 如何将磁流变弹性体用作桥墩主体的新型支撑结构(可控支座), 从而提高墩-梁结构的隔振性能, 还有待进一步研究。

为了探索其实际工程应用的可行性, 搭建桥梁隔振系统对新型支座进行试验研究是不可或缺的环节。但在试验室中设计等比例的桥梁隔振系统难以实现^[7], 而简单的比例缩小试验也不能反映出实际桥梁的隔振特性。因此, 对其进行相似性研究是解决工程问题模型化的有效途径:如韩强等^[8]为研究不同地震烈度对连续桥梁的影响而进行了室内梁桥模型的搭建; 李哲等^[9]采用相似理论对岸桥结构进行了缩尺模型研究; Polley等^[10]对车辆轮胎动力学进行了比例模型化研究; 冷曦晨等^[11]对桩基承载力模拟试验中的相似性问题进行了研究。但将相似理论与可控的磁流变隔振方法相结合研究桥梁的隔振问题还鲜见报道。因此, 如何模型化设计分析基于磁流变支座的桥梁隔振问题, 仍需进一步研究。

三跨桥梁是桥梁隔振系统研究中的一类典型代表。本文针对基于磁流变支座的三跨桥梁的可控隔振难题, 采用无量纲相似理论, 通过比例模型设计、动力学计算仿真和小尺度模拟试验结合的方式进行了相关探索。

1 三跨桥梁隔振系统模型

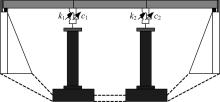
以三跨桥梁为例, 研究地震激励下隔振系统模型化的相似和隔振性能特征, 具体过程为:通过相似理论, 考虑关键的相似元素, 搭建小尺度桥梁隔振试验平台; 对小尺度桥梁隔振试验平台进行相似性和隔振效果评价, 以确保能够反推到真实三跨桥中。隔振试验平台的设计方法如图1所示。对于三跨桥梁, 在进行一定假设后可等效为等价机械系统, 如图2所示。

	Figure Option View Download New Window
	图1 小尺度桥梁隔振试验平台设计方法Fig.1 Design method of vibration isolation platform for small scale bridge

	Figure Option View Download New Window
	图2 三跨桥梁等价机械系统Fig.2 Equivalent mechanical system of three-span bridge

1.1 振源的模型化

复杂的地震可以分解为若干个正弦振动的叠加。因此, 可以将地震的振动加速度 $P (t)$ 表达为:

$P (t) = \overset{n}{\sum_{i = 1}} P_{i} \sin (ω_{i} t) (1)$

式中: $P_{i}$ 为各频率 $ω_{i}$ 下的振动加速度幅值。

将地震传递给桥梁系统的激振力视为地震产生的加速度与桥梁系统质量的乘积, 其表达式为:

$F (t) = MP (t) (2)$

式中: $M$ 为桥梁系统的质量; $F (t)$ 为地震传递到桥梁系统的激振力。

1.2 隔振系统动力学模型

在各频率下桥梁系统顺桥向的状态方程为:

$M {\overset{\cdot \cdot}{X}}_{i} (t) + C {\overset{\cdot}{X}}_{i} (t) + K X_{i} (t) = F_{vi} (t) (3)$

式中: $M$ 三跨桥梁系统质量的数量矩阵; $C$ 为阻尼的数量矩阵; $K$ 为刚度的数量矩阵; $F_{vi} (t)$ 为载荷向量; ${\overset{\cdot \cdot}{X}}_{i} (t) 、 {\overset{\cdot}{X}}_{i} (t) 、 X_{i} (t)$ 分别为加速度、速度、位移向量。

状态方程的初始条件为:

$\{\begin{array}{l} X_{i} (t) = 0 \\ {\overset{\cdot}{X}}_{i} (t) = 0 \end{array} (4)$

因此由式(3)可以解得状态方程的位移向量为:

$\begin{array}{l} X_{i} (t) = {e^{αt} [U_{1 i} \cos (ω't) + U_{2 i} \sin (ω't)] + \\ M_{1 i} \sin (ω_{i} t) + M_{2 i} \cos (ω_{i} t)} (5) \end{array}$

式中: $U_{1 i} 、 U_{2 i}$ 为积分常数, 由初始条件决定; $\begin{array}{l} α = - \frac{c}{2 m}; ω' = \frac{\sqrt{c^{2} - 4 mk}}{2 m}; M_{1 i} = [(k - m ω_{i}^{2}) A_{F_{i}}] \cdot \\ [(m ω_{i}^{2} {- k)}^{2} + c^{2} ω_{i}^{2}]^{- 1}; M_{2 i} = (- c ω_{i} A_{F_{i}}) [(m ω_{i}^{2} - \\ {k)}^{2} + c^{2} ω_{i}^{2}]^{- 1} 。 \end{array}$

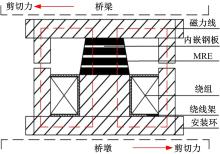
由位移向量(式(5))可以进一步求出速度向量 ${\overset{\cdot}{X}}_{i} (t)$ 和加速度向量 ${\overset{\cdot \cdot}{X}}_{i} (t) 。$

1.3 磁流变支座的模型

自主研发了一种磁流变支座^[12], 其结构的工作原理如图3所示。

	Figure Option View Download New Window
	图3 磁流变支座结构原理图Fig.3 Structure principle of MRB bearing

磁流变弹性体(MRE)与内嵌薄钢板形成基本隔振单元, 受控的激励电流施加到线圈绕组上后, 会产生磁场, 在支座中形成闭环磁路从而调整MRE的流变效应; 铁芯和上、下钢盘等用来承受垂向基础载荷。

磁流变支座提供的隔振力 $F_{R}$ 由磁流变弹性体的黏滞阻尼力 $F_{η}$ 和库伦阻尼力 $F_{τ}$ 组成, 其表达式为:

$F_{R} = F_{η} + F_{τ} (6)$

通过变化激励电流实现库伦阻尼力 $F_{τ}$ 的调控。

2 三跨隔振桥梁的相似设计

由于实际桥梁系统的复杂性, 其动力学参数通常不能都用比例关系进行相似缩小。为了使模型试验能够客观地反映实际规律, 并且便于试验验证, 引入基于无量纲分析的相似理论来设计模型参数。

2.1 系统的相似准则设计

设原三跨桥系统的主要动力学参数包括:质量 $m 、$ 刚度 $k 、$ 阻尼 $c 、$ 力 $A_{F} 、$ 频率 $ω 、$ 时间 $t 、$ 位移 $x 、$ 速度 $\overset{\cdot}{x} 、$ 加速度 $\overset{\cdot \cdot}{x} 。$ 设质量 $(M) 、$ 时间 $(T) 、$ 长度 $(L)$ 为基本量, 可得其他各参数的量纲为: $[m] = M, [k] = M T^{- 2}, [c] = M T^{- 1}, [A_{F}] = ML T^{- 2}, [ω] = T^{- 1}, [t] = T, [x] = L, [\overset{\cdot}{x}] = L T^{- 1}, [\overset{\cdot \cdot}{x}] = L T^{- 2} 。$ 由此可知, 系统的量纲矩阵如表1所示。

表1 设计的量纲矩阵表 Table 1 Designed dimensionless matrix table

	$m$	$k$	$c$	$A_{F}$	$ω$	$t$	$x$	$\overset{\cdot}{x}$	$\overset{\cdot \cdot}{x}$
$M$	1	1	1	1	0	0	0	0	0
$L$	0	0	0	1	0	0	1	1	1
$T$	0	-2	-1	-2	-1	1	0	-1	-2

表1 设计的量纲矩阵表 Table 1 Designed dimensionless matrix table

假设 $m 、 k 、 c 、 A_{F} 、 ω 、 t 、 x 、 \overset{\cdot}{x} 、 \overset{\cdot \cdot}{x}$ 之间满足关系 $φ (m, k, c, A_{F}, ω, t, x, \overset{\cdot}{x}, \overset{\cdot \cdot}{x}) = 0,$ 根据量纲齐次的原则, 可构造 $π = m^{y_{1}} k^{y_{2}} c^{y_{3}} A_{F}^{y_{4}} ω^{y_{5}} t^{y_{6}} x^{y_{7}} {\overset{\cdot}{x}}^{y_{8}} {\overset{\cdot \cdot}{x}}^{y_{9}}$ 为无量纲量, 因此 $y_{1} 、 y_{2} 、 y_{3} 、 y_{4} 、 y_{5} 、 y_{6} 、 y_{7} 、 y_{8} 、 y_{9}$ 为 $Ay = 0$ 的解(设A为量纲矩阵)。

解得系统的 $π$ 矩阵如表2所示。

表2 设计的π 矩阵 Table 2 Designed π matrix

	$m$	$k$	$c$	$A_{F}$	$ω$	$t$	$x$	$\overset{\cdot}{x}$	$\overset{\cdot \cdot}{x}$
$π_{1}$	-1	-1	2	0	0	0	0	0	0
$π_{2}$	1	-1	0	0	2	0	0	0	0
$π_{3}$	-1	1	0	0	0	2	0	0	0
$π_{4}$	0	1	0	-1	0	0	1	0	0
$π_{5}$	1	1	0	-2	0	0	0	2	0
$π_{6}$	1	0	0	-1	0	0	0	0	1

表2 设计的π 矩阵 Table 2 Designed π matrix

因此, 与π 矩阵相应的无量纲量为:

$\{\begin{array}{l} π_{1} = m^{- 1} k^{- 1} c^{2}, π_{2} = m k^{- 1} ω^{2} \\ π_{3} = m^{- 1} k t^{2}, π_{4} = k^{- 1} A_{F} x^{- 1} \\ π_{5} = mk {A_{F}}^{- 2} {\overset{\cdot}{x}}^{2}, π_{6} = m {A_{F}}^{- 1} \overset{\cdot \cdot}{x} \end{array} (7)$

2.2 隔振系统参数的相似关系

设模型化后的台架试验系统参数为:质量 $m_{t} 、$ 刚度 $k_{t} 、$ 阻尼 $c_{t} 、$ 力 $A_{F_{t}} 、$ 频率 $ω_{t} 、$ 时间 $t_{t} 、$ 位移 $x_{t} 、$ 速度 ${\overset{\cdot}{x}}_{t} 、$ 加速度 ${\overset{\cdot \cdot}{x}}_{t} 。$

令实际工程系统和台架试验系统的参数比值分别为:

$\{\begin{array}{l} P_{m} = \frac{m}{m_{t}}, P_{k} = \frac{k}{k_{t}}, P_{c} = \frac{c}{c_{t}} \\ P_{A_{F}} = \frac{A_{F}}{A_{F_{t}}}, P_{ω} = \frac{ω}{ω_{t}}, P_{t} = \frac{t}{t_{t}} \\ P_{x} = \frac{x}{x_{t}}, P_{\overset{\cdot}{x}} = \frac{\overset{\cdot}{x}}{{\overset{\cdot}{x}}_{t}}, P_{\overset{\cdot \cdot}{x}} = \frac{\overset{\cdot \cdot}{x}}{{\overset{\cdot \cdot}{x}}_{t}} \end{array} (8)$

令输入激振频率 $P_{ω}$ 与固有频率之比 $P_{ω_{m}}$ 相等, 即: $P_{ω_{m}} = P_{ω},$ 此时产生的振动最为显著。对于三跨桥梁隔振系统, 台架试验系统的质量和尺寸与实际工程系统存在较大差异, 因此, 令:

$\{\begin{array}{l} P_{ω_{m}} = ξ \\ P_{m} = λ \\ P_{x} = δ \end{array} (9)$

由式(7)(8)(9)可得:

$\{\begin{array}{l} P_{k} = ξ^{2} λ, P_{c} = ξλ \\ P_{A_{F}} = ξ^{2} λδ, P_{t} = ξ^{- 1} \\ P_{\overset{\cdot}{x}} = δξ, P_{\overset{\cdot \cdot}{x}} = δ ξ^{2} \end{array} (10)$

2.3 系统相似性评价指标

采用隔振系统振动位移、加速度作为评价指标, 可较为直观地反映结构力学特性^[13]。具体为:①采用桥面的振动加速度幅频特性; ②采用桥面的振动位移幅频特性; ③计算系统的加速度响应, 即当激振频率为 $ω_{i}$ 时, 桥面振动加速度幅值 $A_{{\overset{\cdot \cdot}{X}}_{i}}$ 与激振源加速度幅值 $A_{i}$ 的比值为:

$η_{{\overset{\cdot \cdot}{x}}_{i}} = A_{{\overset{\cdot \cdot}{X}}_{i}} / A_{i} (11)$

3 系统动力学特性的仿真计算

根据实际桥梁参数, 参照第2节的相似关系, 对桥梁隔振系统进行建模和仿真。

3.1 试验台架的仿真参数

设计仿真参数时, 需要结合实际桥梁系统参数, 又必须考虑实验室实际器件的尺寸、质量和便于测量等因素, 因此按照相似计算方法, 先设定固有频率、质量、位移3个参数的相似比, 具体为:①实际桥梁结构的固有频率较低, 为保持一致性, 设计台架试验系统的固有频率也应低一些, 故令两系统的固有频率之比 $P_{ω_{m}} = 0.5;$ ②实际桥面质量很大, 因此设计台架试验的桥面质量应小三个量级, 故令两系统的质量之比 $P_{m} = 5000;$ ③实际工程系统的桥面振动位移较大, 而考虑实验室实际器件的尺寸、质量等条件, 应使试验系统的位移约为实际工程系统的十分之一, 因此令两振动系统最大位移比 $P_{x} = 16 。$ 进而由式(10)求解两系统间的相似关系, 如表3所示。

表3 两模型的相似关系 Table 3 Similarity relations of two models

物理量	相似关系	相似系数
固有频率 $ω_{m}$	$P_{ω_{m}}$	0.5
浮置板质量 $m$	$P_{m}$	5000
振动位移 $x$	$P_{x}$	16
系统刚度 $k$	$P_{k}$	1250
系统阻尼 $c$	$P_{c}$	2500
时间 $t$	$P_{t}$	2
振动速度 $\overset{\cdot}{x}$	$P_{\overset{\cdot}{x}}$	8
振动加速度 $\overset{\cdot \cdot}{x}$	$P_{\overset{\cdot \cdot}{x}}$	4

表3 两模型的相似关系 Table 3 Similarity relations of two models

表4为某三跨桥梁原型系统的参数。参考相关厂家提供的工程橡胶支座原型实际参数, 给出磁流变支座的结构尺寸主要参数, 如表5所示。因此, 根据相似关系(表3)和实际隔振重要参数(表4), 推导出台架模型的理论参数取值, 如表6所示。

表4 实际桥梁系统的重要参数 Table 4 Important parameters of an actual bridge system

表5 磁流变支座的主要参数 Table 5 Important parameters of MRB

表6 试验装置的参数 Table 6 Parameters of experiment apparatus

3.2 两系统动力学相似性对比

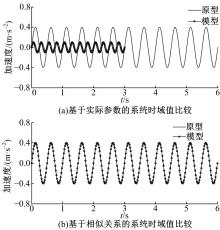
分别从桥面振动的加速度和位移两方面验证设计的两系统动力学特性具有相似性。对于桥面振动加速度, 假设实际工程系统在某单一正弦位移激励 $x (t) = 0.16 \sin (2 π t)$ 下振动, 则根据相似关系, 对应于台架试验系统应施加的位移激励为 $x (t) = 0.01 \sin (4 π t);$ 对于桥面振动位移, 考虑到地震的复杂性, 假设此时实际工程在复合激励 $x (t) = 0.16 \sin (2 π t) + 0.16 \sin (4 π t)$ 下振动, 则对应的台架试验系统应施加的位移激励为:

$x (t) = 0.01 \sin (2 π t) + 0.01 \sin (4 π t) (12)$

运用Matlab对隔振相似模型和实际桥梁原型进行仿真计算, 得到其对比关系, 其时域加速度值如图4所示。时域位移值如图5所示。对比图4与图5可知, 经过相似计算分析后, 相似模型与原型的力学特性值较为吻合。

	Figure Option View Download New Window
	图4 时域加速度值Fig.4 Acceleration in time domain

	Figure Option View Download New Window
	图5 时域位移值Fig.5 Displacement in time domain

4 桥梁隔振系统的台架模拟试验

在对隔振系统进行无量纲相似参数设计和仿真计算的基础上, 开展了小尺度桥梁隔振试验研究。

4.1 台架模拟试验条件分析

虽然可以通过理论计算确定隔振相似关系, 在对桥梁进行模型试验研究时, 受条件、经济等因素制约和模型参数之间的相互影响, 很难做到模型与实物完全相似^[14]。结合振动知识, 在试验台搭建的过程中, 着重考虑磁流变支座刚度和阻尼的相似关系, 兼顾桥墩的质量和桥面的长度、质量等的相似关系, 弱化各部件其他属性(如密度、强度等)的相似关系。

因此, 综合考虑由式(10)得到的相似关系(见表3)、实际工程系统参数(见表4)以及市面上现有材料的情况, 选取钢板作为制作桥面的材料, ABS(丙烯腈-丁二烯-苯乙烯共聚物)作为制作桥墩的材料。台架试验装置的主要参数如表6所示。

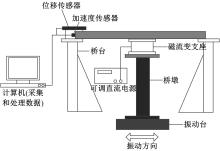
由于试验条件和经费的限制, 选取最大振幅为10 mm, 振动频率在1~100 Hz间可调, 台面长度和宽度各为1 m的水平单向正弦波激振台模拟地震激励。受激振台台面尺寸的约束, 难以在激振台上设置两个桥墩。由式(5)可知, 桥墩的总质量、刚度、阻尼一致时, 不会对桥面的振动位移和加速度产生大的影响, 因此可以将三跨桥梁的两个桥墩简化为单墩。小尺度桥梁隔振台架试验装置实物如图6所示, 试验原理如图7所示。激振台下端放置于地基上, 上端与桥墩底部连接, 桥墩上放置钢板(模拟梁面), 磁流变支座放置于钢板与桥墩间。桥面上分别安装有加速度传感器和位移传感器。试验时, 激振台将水平振动传递给桥墩及台架试验系统, 磁流变支座工作在剪切模式下, 在测量桥面振动加速度和振动位移后, 通过控制装置实现对磁流变支座的在线隔振调控。

	Figure Option View Download New Window
	图6 小尺度桥梁隔振试验平台实物图Fig.6 Bench test apparatus of small-scale bridge in laboratory

	Figure Option View Download New Window
	图7 小尺度桥梁隔振试验原理图Fig.7 Schematic diagram of vibration test for small-scale bridge

图8(a)为自主研发的磁流变支座, 磁流变弹性体被内部线圈缠绕, 当不加电流时可视为被动支座; 磁流变支座在不同控制电流下的力学特性可经液压伺服力学测试机(MTS)试验测得。由于本文的重点是研究小尺度隔振试验平台与实际原型系统的相似性并验证磁流变支座的隔振效果, 因此在试验中磁流变支座的控制特性可简化为不同恒定控制电流与其刚度和阻尼的关系, 试验测得该关系如表7所示。图8(b)为加速度传感器, 加速度传感器采用能够测量± 5g(g=9.8 m/s²)的LC0809型内置压电加速度传感器, 灵敏度能够达到0.001g。图8(c)为LVDT型位移传感器, 测量范围为[-15, 15] mm, 精度可达到0.05%。

	Figure Option View Download New Window
	图8 主要试验器件Fig.8 Main experiment devices

表7 磁流变支座的控制特性 Table 7 Control characteristics of MRB

4.2 台架试验理论计算值与实际测量值对比

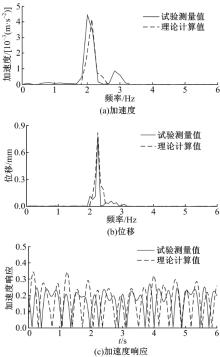
调整激振台, 输入振幅为10 mm、频率为2 Hz和3 Hz叠加的复合正弦振动。对传感器测量的数据进行滤波后, 与理论计算的加速度和位移进行对比。加速度、位移以及加速度响应的对比结果如图9所示, 结果显示, 参数指标基本吻合(相似度可达到80%以上)。可通过改进试验条件来提高这些指标的相似度。

	Figure Option View Download New Window
	图9 桥面加速度位移及加速度响应的试验值与理论值对比Fig.9 Acceleration, displacement and acceleration response of bridge deck in experiment and in theory

4.3 台架试验隔振效果

选取桥面振动位移、桥面振动加速度系统加速度响应和支座剪切力作为隔振效果的评价指标。

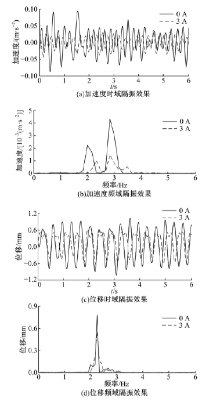
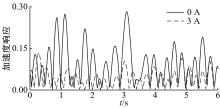
采取给支座通以恒定电流的控制方式, 当给磁流变支座通以3 A的电流时, 对加速度传感器测得结果滤波后, 其时域对比如图10(a)所示, 频域对比如图10(b)所示; 对位移传感器测得结果滤波后, 其时域对比如图10(c)所示, 频域对比如图10(d)所示。

	Figure Option View Download New Window
	图10 隔振效果对比Fig.10 Comparison of vibration isolation effect

调整振动试验台, 施加2 Hz、10 mm的振动, 由式(11)计算得到的加速度响应对比值, 如图11所示。

	Figure Option View Download New Window
	图11 加速度响应Fig.11 Acceleration response of system

由于试验条件的限制, 没有安装剪切力测试仪, 故对于支座的剪切力采取间接计算的方式获得。计算公式为:

$F_{m} = k_{n} \times (L_{m} - L_{n}) (13)$

式中: $F_{m}$ 为支座的剪切力; $k_{n}$ 为支座的刚度; $L_{m}$ 为桥面振动位移; $L_{n}$ 为振动试验台的振动位移。

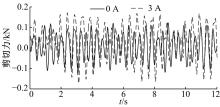
计算所得剪切力的时域图如图12所示。当支座剪切力增大时, 剪力-位移滞回曲线面积变大, 表明支座对地震能量的耗散能力增强^[15]。

	Figure Option View Download New Window
	图12 磁流变支座的剪切力Fig.12 Shear stress of MRB

从图10~图12可以看出, 给磁流变支座通以电流之后, 桥面振动加速度峰值最大减小42%, 桥面振动位移峰值最大减小36%, 支座剪切力峰值最大增加41%, 大大降低了振动对桥梁结构的危害。

5 结束语

推导出了基于相似理论的三跨桥隔振原型与小尺度试验模型的主要关系, 设计了小型隔振模拟试验系统, 对比分析了桥面振动加速度和位移的理论值与实测值的相似性, 结果表明其具有良好的一致性, 说明试验系统能够揭示出桥梁可控隔振原型的主要隔振性能。

基于磁流变支座的三跨桥梁隔振系统相对于传统的被动隔振, 桥面振动加速度峰值最大减小了42%, 振动位移峰值最大减小了36%, 支座剪切力峰值最大增加了46%。表明磁流变支座在降低桥梁振动和提升地震能量耗散能力方面具有明显效果。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	卢凯良, 张卫国, 吴志君, 等. 集装箱起重机减隔震装置及其模型试验[J]. 振动、测试与诊断, 2011, 31(4): 501-506. Lu Kai-liang, Zhang Wei-guo, Wu Zhi-jun, et al. Anti-seismic device design for container crane and its model test[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(4): 501-506. [本文引用:1]
[2]	Ju B X, Yu M, Fu J, et al. A novel porous magnetorheological elastomer: preparation and evaluation[J]. Smart Materials and Structures, 2012, 21(3): 035001. [本文引用:1]
[3]	王修勇, 陈政清, 何旭辉, 等. 斜拉桥拉索风雨振控制的智能阻尼技术[J]. 振动与冲击, 2002, 21(3): 26-30. Wang Xiu-yong, Chen Zheng-qing, He Xu-hui, et al. Control of wind-rain-induced vibration of stay cables on cable-stayed bridge using smart damping[J]. Journal of Vibration and Shock, 2002, 21(3): 26-30. [本文引用:1]
[4]	陈琳. 磁流变弹性体的研制及其力学行为的表征[D]. 合肥: 中国科学技术大学工程科学学院, 2009. Chen Lin. The development and mechanical characterization of magnetorheological elastomers[D]. Hefei: School of Engineering Science, University of Science and Technology of China, 2009. [本文引用:1]
[5]	龚兴龙, 邓华夏, 李剑锋, 等. 磁流变弹性体及其半主动吸振技术[J]. 中国科学技术大学学报, 2007, 37(10): 1192-1203. Gong Xing-long, Deng Hua-xia, Li Jian-feng, et al. Magnetorheological elastomers and corresponding semi-active vibration absorption technology[J]. Journal of University of Science and Technology of China, 2007, 37(10): 1192-1203. [本文引用:1]
[6]	Li Y, Li J, Tian T, et al. A highly adjustable magnetorheological elastomer base isolator for applications of real-time adaptive control[J]. Smart Materials and Structures, 2013, 22(9): 095020. [本文引用:1]
[7]	李锐, 杜鹏飞, 徐文韬, 等. 基于相似理论的短型浮置板磁流变隔振试验研究[J]. 仪器仪表学报, 2014, 35(1): 200-207. Li Rui, Du Peng-fei, Xu Wen-tao, et al. Magneto-rheological vibration isolation model experimental study on discrete floating slab based on similarity theory[J]. Chinese Journal of Scientific Instrument, 2014, 35(1): 200-207. [本文引用:1]
[8]	韩强, 杜修力, 刘文光, 等. 不同地震烈度下隔震连续梁桥模型振动台试验[J]. 中国公路学报, 2008, 21(6): 50-56. Han Qiang, Du Xiu-li, Liu Wen-guang, et al. Shaking table test of isolated continuous girder bridge model under different earthquake intensity excitations[J]. China Journal of Highway and Transport, 2008, 21(6): 50-56. [本文引用:1]
[9]	李哲, 胡吉全, 王东, 等. 地震载荷作用下岸桥结构单参数畸变相似模型研究[J]. 振动与冲击, 2014, 33(20): 164-169. Li Zhe, Hu Ji-quan, Wang Dong, et al. Distortion model of container cranes subjected to seismic load[J]. Journal of Vibration and Shock, 2014, 33(20): 164-169. [本文引用:1]
[10]	Polley M, Alleyne A G. Dimensionless analysis of tire characteristics for vehicle dynamics studies[C]∥Proceeding of the 2004 American Control Conference, Boston, USA, 2004: 3411-3416. [本文引用:1]
[11]	冷曦晨, 佴磊, 亓宾. 桩基承载力模拟试验中相似性问题[J]. 吉林大学学报: 地球科学版, 2005, 35(4): 491-495. Leng Xi-chen, Nie Lei, Qi Bin. Similarity in the simulation test for bearing capacity of pile foundation[J]. Journal of Jilin University (Earth Science Edition), 2005, 35(4): 491-495. [本文引用:1]
[12]	李锐, 牟文俊, 陈世嵬, 等. 小尺度磁敏弹性体支座的结构设计及性能分析[J]. 仪器仪表学报, 2016, 37(10): 2399-2406. Li Rui, Mu Wen-jun, Chen Shi-wei, et al. Research on structure design and performance of a small-scale magneto-rheological elastomeric bearing[J]. Chinese Journal of Scientific Instrument, 2016, 37(10): 2399-2406. [本文引用:1]
[13]	宋彦君, 刘寒冰, 谭国金, 等. 基于应变计的梁式桥位移响应测试方法[J]. 吉林大学学报: 工学版, 2012, 42(增刊1): 198-201. Song Yan-jun, Liu Han-bing, Tan Guo-jin, et al. Displacement response test method of beam bridge based on a strain gauge[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(Sup. 1): 198-201. [本文引用:1]
[14]	黄俊明, 周孔亢, 徐兴, 等. 空气悬架固有频率试验研究及理论分析[J]. 机械工程学报, 2011, 47(14): 114-119. Huang Jun-ming, Zhou Kong-hang, Xu Xing, et al. Theoretical analysis and test research of eigen-frequency of air suspension[J]. Journal of Mechanical Engineering, 2011, 47(14): 114-119. [本文引用:1]
[15]	高欣, 吴晓伟, 田俊. 轻骨料混凝土剪力墙非线性有限元模型的构成及影响其抗震性能的因素[J]. 吉林大学学报: 工学版, 2015, 45(5): 1428-1435. Gao Xin, Wu Xiao-wei, Tian Jun. Structure of nonlinear finite element model of lightweight aggregate concrete share wall and the factors affecting seismic performance[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(5): 1428-1435. [本文引用:1]

2011

0.0

. 2011, 31(4):501-506

Anti-seismic device design for container crane and its model test

集装箱起重机减隔震装置及其模型试验

Lu Kai-liang , Zhang Wei-guo , Wu Zhi-jun

卢凯良, 张卫国, 吴志君

... 0 引言通过增加结构强度或采用被动支承(支座)来提高系统的抗振能力,是桥梁等机械系统隔减振设计中的常用手段^[1] ...

2012

0.0

... 但是,被动支承(支座)在各种大的突发振动冲击载荷作用下,缺乏智能调节横向刚度/强度来抵制剪切破坏力和过度移位的能力,也难以通过增加阻尼来耗散瞬间有害能量,其隔振、抗害能力不足^[2],成为结构安全体系中最薄弱的环节 ...

2002

0.0

. 2002, 21(3):26-30 DOI:doi:10.3969/j.issn.1000-3835.2002.03.007

Control of wind-rain-induced vibration of stay cables on cable-stayed bridge using smart damping

斜拉桥拉索风雨振控制的智能阻尼技术

Wang Xiu-yong , Chen Zheng-qing , He Xu-hui

王修勇, 陈政清, 何旭辉

洞庭湖大桥自建成通车以来已发生多次严重风雨振,必须采取有效的振动控制措施.本文应用磁流变阻尼器对该桥风雨振控制进行了仿真和现场试验研究,得到了拉索-阻尼器系统模态阻尼比随阻尼器输入电压的变化关系,显示磁流变阻尼器能提供足够的可变阻尼对拉索进行智能控制,在实际风雨振时的现场观测结果显示磁流变阻尼器对风雨振具有很好的减振效果,实测的加速度响应表明安装阻尼器拉索的加速度响应仅为未加阻尼器拉索的1/20～30.洞庭湖大桥已计划全桥安装磁流变阻尼器,它将是世界上首座应用该阻尼器进行风雨振阻尼控制的桥梁.

... 目前,有将磁流变阻尼器作为桥梁拉索附加减振装置的报道^[3],但未从根本上考虑桥的墩-梁结构隔振问题 ...

2009

0.0

. 2009, :- DOI:doi:10.7666/d.y1498536

The development and mechanical characterization of magnetorheological elastomers

磁流变弹性体的研制及其力学行为的表征

Chen Lin

陈琳

磁流变弹性体是一类智能材料。它是由高分子聚合物和软磁性颗粒组成,在外加磁场的作用下,其模量和阻尼等性能会发生变化。目前已有不少研究者利用磁流变弹性体的变刚度特性,设计了调频式动力吸振器和汽车悬挂轴衬等器件。因此,磁流变弹性体在振动控制等工程领域具有良好的应用前景。磁流变弹性体要实现工程化,一方而需要具备显著的磁流变效应(一般指模量在磁场下的可控范围),另一方面需要具备优异的综合性能。而目前磁流变弹性体的磁流变效应仍不够大,同时多数研究者仅考虑了其模量,忽略了同样重要的阻尼特性和机械性能。在磁流变弹性体机理研究方面,现有模型往往存在过多的假设,影响了结果的可靠性。为解决上述存在问题,本文建立了一套适合于高弹高韧类材料为基体的磁流变掸性体的研制系统,并对磁流变弹性体进行了初步制备;研究了多种制备和测试参数下磁流变弹性体的磁流变效应等力磁耦合性能与机械性能,同时分别通过动态实验和数值模拟的方法研究了磁流变弹性体的阻尼特性;基于观测到的微观结构建立了两种磁流变弹性体的磁致模型;最后根据上述研究成果对材料进行了进一步优化发计,得到了综合性能良好的磁流变弹性体。本文首先概述了磁流变材料的历史、分类和应用,着重介绍了磁流变弹性体的最新研究进展以及存在的科学和应用问题。建立了一套适用于以天然橡胶为代表的高弹高韧类材料为基体的磁流变弹性体的研制系统。在制备基体/颗粒的粘塑态磁性混合物时,分别通过了溶剂法和混炼法两种途径。从性能、工艺、效率和可行性等方面,比较了两种方案的优劣,并最终采用了混炼法。组建了热磁耦合预结构化和固化系统,探索出了基于高弹高韧基体材料的磁流变弹性体的研制方案,并进行了初步制备。实验研究了包括预结构磁场强度、温度、增塑剂和铁粉含量的制备参数和包括动态应变和激励频率的测试参数对磁流变弹性体动态力学性能的影响。此外,搭建了准静态力磁耦合剪切装置,实验研究了不同铁粉含量的磁流变弹性体在有无外场下的准静态应力—应变关系;评估了磁流变弹性体的拉伸强度、撕裂强度、硬度、回弹性、抗热氧老化和耐磨耗性能等基本机械性能。通过扫描电镜观测了不同磁感应强度下制备的磁流变弹性体中磁性颗粒形成的微观结构。发现在预结构过程中施加磁场后,颗粒逐渐团聚成柱状结构。随着施加的磁感应强度的增大,颗粒柱状结构的宽度和长度也随之增大。基于观测到的微观结构,舍弃了袭用于磁流变液的颗粒贯穿模型,建立了适用于磁流变弹性体的力学模型。首先建立了有限柱长模型。在有限柱长模型中,假设磁流变弹性体内包含若干段宽度相同长度随机分布的柱状结构。通过等效磁导率的方法推导出了磁流变弹性体的磁致应力和磁致模量的表达式。接着对磁流变弹性体结构与性能这一问题作了进一步深入的研究。发现对于任何一块磁流变弹性体,其中包含的柱状颗粒结构的长度呈高斯分布。据此建立了一种普遍性更高的磁流变弹性体高斯分布模型。通过该模型研究了颗粒柱结构长度、宽度、外加磁场强度以及应变对磁流变弹性体磁致性能的影响。与传统的Jolly和Davis模型相比,高斯分布模型具有更好的精度和更广的使用范围。分别通过动态实验和数值模拟的方法研究了磁流变弹性体的阻尼特性。相关实验研究结果表明,除刚度可控外,磁流变弹性体也是一种阻尼可控的材料。据此提出了与外加磁场相关的新界面滑移假设。通过对磁流变弹性体取三维代表体积单元,使用有限元软件计算其在受到周期动态剪切应变时的响应。计算结果显示,应力应变的曲线最终收敛于一个迟滞回线。由此计算出了磁流变弹性体的不加磁场时的阻尼比,且比较接近于实验结果。最后基于以上的理论和实验结果,结合应用需求,对磁流变弹性体进行了进一步优化设计。特别是在制备磁流变弹性体时,通过添加适量的炭黑来改性基体性能,可以同时增强磁流变效应,降低损耗因子,以及提高拉伸强度。这对于解决磁流变效应、损耗因子以及机械强度之间的矛盾提供了一种理想方案,对于基于磁流变弹性体设计的调频式动力吸振器有着十分重要的意义。

... 磁流变弹性体(Magneto-rheological elastomers,MRE)由磁性颗粒(如羰基铁粉)和聚合介质(如橡胶)等材料复合制成^[4],在磁场作用下其刚度阻尼特性可控,且具有响应快、可逆性好、可控能力强、稳定性好等优点^[5],已成为结构抗震减灾领域研究的新热点,如有学者研究了基于MRE支座的房屋建筑结构隔振技术,为磁流变支座用于大型路桥建筑结构抗震探索了新方向^[6] ...

2007

0.0

. 2007, 37(10):1192-1203

Magnetorheological elastomers and corresponding semi-active vibration absorption technology

磁流变弹性体及其半主动吸振技术

Gong Xing-long , Deng Hua-xia , Li Jian-feng

龚兴龙, 邓华夏, 李剑锋

2013

0.0

2014

0.0

. 2014, 35(1):200-207 DOI:doi:10.3969/j.issn.0254-3087.2014.01.028

Magneto-rheological vibration isolation model experimental study on discrete floating slab based on similarity theory

基于相似理论的短型浮置板磁流变隔振试验研究

Li Rui , Du Peng-fei , Xu Wen-tao

李锐, 杜鹏飞, 徐文韬

运用参数可调的磁流变装置对提高地铁浮置板轨道系统的隔振性能具有重要意义。针对实验室对系统原型研究难以实现的问题,基于无量纲分析的相似理论,从反映动力学特性的物理量量纲角度出发,以振动力传递率和相对加速度传递率作为评价指标,推导出浮置板轨道隔振原型系统和小尺度试验台架模拟系统间的相似关系,并以该相似关系为基础来指导试验台架模型设计。运用MATLAB分别对两系统进行动力学理论计算,仿真表明原型和模拟模型的动力学特性具有较好的相似性。进一步根据设计的模型参数,搭建小尺度试验台架,台架试验结果和理论计算值具有较好的一致性。研究表明,根据相似理论搭建的试验模型能够反映轨道隔振原型的主要隔振性能。

... 但在试验室中设计等比例的桥梁隔振系统难以实现^[7],而简单的比例缩小试验也不能反映出实际桥梁的隔振特性 ...

2008

0.0

. 2008, 21(6):50-56

Shaking table test of isolated continuous girder bridge model under different earthquake intensity excitations

不同地震烈度下隔震连续梁桥模型振动台试验

Han Qiang , Du Xiu-li , Liu Wen-guang

韩强, 杜修力, 刘文光

... 因此,对其进行相似性研究是解决工程问题模型化的有效途径:如韩强等^[8]为研究不同地震烈度对连续桥梁的影响而进行了室内梁桥模型的搭建 ...

2014

0.0

. 2014, 33(20):164-169 DOI:doi:10.13465/j.cnki.jvs.2014.20.031

Distortion model of container cranes subjected to seismic load

地震载荷作用下岸桥结构单参数畸变相似模型研究

Li Zhe , Hu Ji-quan , Wang Dong

李哲, 胡吉全, 王东

According to the dynamic similarity theory to design the reasonable scale model, take dynamic test analysis of the container crane structure by shaking table. In the scale model, the length of each component (beam) size can be based on the size of the prototype, but the cross-section thickness cannot change according to the same scale narrowed, causing distortion model. Finite element prediction coefficient method can get the prediction coefficient which using to the distortion model predict the dynamic characteristics of prototype. In order to verify the effectiveness of distortion coefficient that obtained by the finite element prediction coefficient method, made a distortion model that the thickness of the cross-section distorted and a hammering modal test and a series of seismic sharking table tests were successively carried out. The results showed that the experimental results similar to the calculation results, the maximum acceleration and strain in the same position, distortion coefficient of prediction is reasonable.

据动力相似理论设计合理的缩尺模型，用振动台模型对岸桥结构进行动力学试验分析。设计中的缩尺模型各构件（梁）长度可基于原形尺寸由相似比尺推导获得，而梁截面厚度却不能与长度按同一比尺缩小，致使模型产生畸变。采用有限元预测系数法获得畸变模型的动响应预测系数从而可预测原型的动态特性。为验证用该方法所得预测系数的有效性，以相似理论制作缩尺模型并使截面厚度产生畸变，对畸变模型进行锤击模态及地震振动台试验分析。结果表明，试验结果与有限元计算结果相近，结构发生最大加速度、应变位置相似，表明畸变预测系数合理。

... 李哲等^[9]采用相似理论对岸桥结构进行了缩尺模型研究 ...

2004

0.0

... Polley等^[10]对车辆轮胎动力学进行了比例模型化研究 ...

2005

0.0

. 2005, 35(4):491-495 DOI:doi:10.3969/j.issn.1671-5888.2005.04.014

桩基承载力模拟试验中相似性问题

Leng Xi-chen , Nie Lei , Qi Bin

冷曦晨, 佴磊, 亓宾

The similarity problem, existing in the simulation tests for bearing capacity of pile foundation, is studied. The emphasis is on the following three major aspects such as the similarity of the environments between test and engineering pile, the similarity between shearing friction test and the side friction force of engineering pile and the similarity between the triaxial test and endbearing capacity of pile. The study shows that in the simulation test the samples should be undisturbed and the state of the stress in test should be consistent to that of the engineering for the test of pile side friction in the simulation test. For endbearing capacity of pile, the samples should be undisturbed, but the confining pressure of samples is shrank according to geometry similarity constant, so as to obtain the practical endbearing capacity of pile by multiplying the test results.

通过对桩基承载力模拟试验中相似性问题的研究，重点探讨了试验与工程桩所处环境的相似性, 剪切摩擦试验与工程桩桩侧摩阻力的相似性以及三轴试验与桩端承载力的相似性等三个主要的相似问题。研究表明对于模拟试验中桩侧摩阻力的试验，应采用原状样，并保持应力与工程应力状态一致。对于端承力则应采用原状样，但将围压按几何相似常数缩小，并将端承力试验结果按该相似常数扩大以作为实际工程桩的端承力。

... 冷曦晨等^[11]对桩基承载力模拟试验中的相似性问题进行了研究 ...

2016

0.0

. 2016, 37(10):2399-2406

Research on structure design and performance of a small-scale magneto-rheological elastomeric bearing

小尺度磁敏弹性体支座的结构设计及性能分析

Li Rui , Mu Wen-jun , Chen Shi-wei

李锐, 牟文俊, 陈世嵬

... 3 磁流变支座的模型自主研发了一种磁流变支座^[12],其结构的工作原理如图3所示 ...

2012

0.0

. 2012, 42(增刊1):198-201

Displacement response test method of beam bridge based on a strain gauge

基于应变计的梁式桥位移响应测试方法

Song Yan-jun , Liu Han-bing , Tan Guo-jin

宋彦君, 刘寒冰, 谭国金

摘　要：首先利用梁式桥位移、应变与挠曲曲率的力学关系,建立了由实测应变计算桥梁位移的数学模型。再利用广义最小二乘原理实现模型的求解,最终形成利用应变计算的梁式桥位移响应测试方法。最后通过数值算例验证了所提出方法的可行性和准确性,其精度可以满足工程应用的要求。本方法无需任何位移测量仪器,只利用已有的应变数据便能实时地分析出桥梁位移。

... 3 系统相似性评价指标采用隔振系统振动位移、加速度作为评价指标,可较为直观地反映结构力学特性^[13] ...

2011

0.0

. 2011, 47(14):114-119 DOI:doi:10.3901/JME.2011.14.114

Theoretical analysis and test research of eigen-frequency of air suspension

空气悬架固有频率试验研究及理论分析

Huang Jun-ming , Zhou Kong-hang , Xu Xing

黄俊明, 周孔亢, 徐兴

摘　要：汽车空气悬架的固有频率是表征车辆平顺性和道路友好性的一个重要指标,为能正确获取悬架的固有频率,在总结国内外相关标准的基础上从激励方式和数据处理方法两方面分析和比较目前国内沿用的GB 4783—1984（汽车悬挂系统的固有频率和阻尼比测定方法）悬架固有频率试验标准和欧洲委员会的96/53/EC、澳大利亚的VSB11标准,并对电子控制空气悬架的大客车进行整车阶跃试验。针对试验数据处理中发现的俯仰角振动问题通过半车模型仿真来进行理论分析以及车身俯仰角振动固有频率试验,探讨按照国家标准和国外标准进行数据处理分析时存在的局限性,通过辅助试验获得正确的悬架固有频率。为电子控制空气悬架大客车类的悬架固有频率试验方法以及试验数据的处理分析方法提出补充的建议和辅助试验手段。

... 1 台架模拟试验条件分析虽然可以通过理论计算确定隔振相似关系,在对桥梁进行模型试验研究时,受条件、经济等因素制约和模型参数之间的相互影响,很难做到模型与实物完全相似^[14] ...

2015

0.0

. 2015, 45(5):1428-1435

Structure of nonlinear finite element model of lightweight aggregate concrete share wall and the factors affecting seismic performance

轻骨料混凝土剪力墙非线性有限元模型的构成及影响其抗震性能的因素

Gao Xin , Wu Xiao-wei , Tian Jun

高欣, 吴晓伟, 田俊

... 当支座剪切力增大时,剪力-位移滞回曲线面积变大,表明支座对地震能量的耗散能力增强^[15] ...