硅片自旋转磨削中基于力的微接触机理

引用本文

任庆磊, 魏昕, 谢小柱, 胡伟. 硅片自旋转磨削中基于力的微接触机理[J].吉林大学学报（工学版）, 2018,48(3): 796-802
REN Qing-lei, WEI Xin, XIE Xiao-zhu, HU Wei. Micro contact mechanism based on force in self rotation grinding of silicon wafer[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 796-802 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20171132
Permissions

硅片自旋转磨削中基于力的微接触机理

任庆磊, 魏昕, 谢小柱, 胡伟

广东工业大学机电工程学院,广州 510006

作者简介:任庆磊(1981-),男,博士研究生.研究方向:超精密加工技术.E-mail:15920179558@139.com

基金:国家自然科学基金项目(U0734008); 广东省自然科学基金项目(8151009001000048); 广东工业大学校青年基金项目(082042).

摘要

建立了杯型金刚石砂轮稳定延性域磨削过程中砂轮微单元与硅片的微接触力学模型,采用力分解法研究了其自旋转磨削微观作用机理。法向分解分别运用接触力学中的赫兹理论和“空腔模型”理论分析得出硅片上对应弹性和塑性阶段的载荷和应力分布情况,以及砂轮微单元上相应的应力分布情况;切向分解运用微观摩擦学理论分析得出滑动摩擦力以及法、切向合成微接触总应力的情况。分析与试验对比结果证明了本文方法有效,可为硅片自旋转磨削机理研究提供理论支撑。

关键词: 机械制造及自动化; 自旋转磨削; 微接触; 硅片; 砂轮微单元

中图分类号:TG580.1 文献标志码:A 文章编号:1671-5497(2018)03-0796-07

Micro contact mechanism based on force in self rotation grinding of silicon wafer

REN Qing-lei, WEI Xin, XIE Xiao-zhu, HU Wei

School of Electro-mechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China

Abstract

Self rotating grinding with cup type diamond wheel is a typical ultra precision grinding process for silicon wafer. In this paper, a mechanical model of the micro contact between the wheel micro unit and silicon wafer was established for the stable ductile grinding process, and the mechanism of self rotating grinding was studied using force decomposition method. On the normal direction, the load and stress distribution of the corresponding elastic and plastic stages were obtained using the Hertz theory and the cavity model respectively. On the tangential direction, the sliding friction force was obtained using micro tribology theory. The load in the two directions was synthesized and the total stress condition was obtained. The analysis results were verified by corresponding experiment and simulation.

Keyword: mechanical manufacture and automation; self rotating grinding; micro contact; silicon wafer; wheel micro unit

文章图片

0 引言

目前, 绝大多数的集成电路(IC)芯片的衬底材料都采用单晶硅片, 而单晶硅片的质量直接决定芯片的性能和成品率^[1]。传统的硅片加工多采用研磨、腐蚀等工艺, 但加工效率低, 尤其对大直径(φ ≥ 300 mm)硅片的加工, 而采用超精密磨削加工会比传统加工效益更优, 其中应采用杯型金刚石砂轮进行硅片自旋转磨削是典型的硅片超精密磨削加工形式^[2]。采用杯型金刚石砂轮进行硅片自旋转磨削加工的方式是由日本学者Matsui首先提出^[3], 硅片在真空作用下吸附在旋转工作台上, 硅片的直径略小于旋转工作台的直径, 两者的中心重合。调整砂轮内外沿(工作面)的中心轴线, 使其与硅片中心对齐。磨削加工中, 砂轮与硅片都绕各自的中心轴线旋转, 砂轮只做轴向进给运动。这种自旋转磨削方式可通过调节硅片转速与砂轮轴向进给速度来控制磨削深度, 从而可实现以塑性去除方式的延性域磨削。

在硅片自旋转磨削加工的应用过程中, 其磨削加工机理是研究的重点, 备受国内外研究学者关注^[4]。其中, 国外代表性的是Pei等^[5]通过改变加工的多因素参数进行了一系列磨削试验, 系统研究了磨削加工工艺对硅片表面质量的各种影响。国内代表性的是康仁科等为获得高质量超薄硅片进行了大量自旋转磨削工艺试验研究^[6]。这些研究为获得直观的高质量硅片偏重于试验性。而对硅片自旋转磨削加工机理的理论性研究主要集中在硅片材料去除机理方面, 包括以“ 压痕断裂模型” 为基础的脆性去除机理及延性域的塑性去除机理^[7], 这些机理研究的工作是采用压痕和划痕试验构建经验公式的形式找出硅片的材料去除规律, 但由于其磨削过程的复杂性, 磨削加工机理研究仍未形成统一的认识。同时, 硅片材料去除机理研究所依托的微观模型主要是磨粒与硅片间的两体模型, 侧重于对磨削中硅片的微观影响研究, 欠缺对磨削中砂轮的微观影响研究^[8]。

基于此, 本文从稳定延性域磨削过程中抽取出砂轮微单元与硅片的微接触作为研究对象, 提出并建立了微观三体力学模型, 应用力分解法对自旋转磨削过程中砂轮与硅片的微观相互作用机理进行了理论分析研究, 为硅片自旋转磨削中硅片材料去除机理及砂轮磨损研究提供相关理论支撑。

1 力学模型

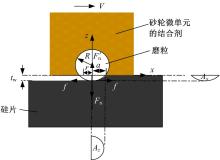
为建立三体力学模型, 在硅片自旋转稳定磨削过程中, 从砂轮与硅片的接触加工区域中提取出包含单颗磨粒的砂轮微单元作为研究对象。提取过程是从宏观砂轮端面上取包含单颗磨粒的结合剂, 如图1所示, 由一定体积的结合剂把持单颗金刚石磨粒组成。结合剂的体积由砂轮浓度、磨粒半径 $R$ 及金刚石密度决定。这里假定:宏观砂轮的端面结合剂是均实平整的; 宏观砂轮中金刚石微粉磨粒分布是均匀的, 形状为球形, 出刃高度为粒径的三分之一。

	Figure Option View Download New Window
	图1 砂轮微单元的提取Fig.1 Extraction of wheel micro unit

提取出的砂轮微单元与硅片在延性域磨削中产生微接触。砂轮微单元与硅片微接触的理想力学模型如图2所示, 其中, A_z为法向接触面积; A_x为切向接触面积。这里假定延性域去除的硅材料是塑性的。

	Figure Option View Download New Window
	图2 微接触力学模型Fig.2 Micro contact mechanics model

延性域磨削中, 砂轮微单元是以速度 $V$ 和磨削深度(切深) $t_{w}$ 塑性去除硅片的, 对此过程进行分解分析。法向 $z$ 方向, 假设砂轮微单元整体是以切深的距离 $t_{w}$ 压入硅片, 与硅片间形成法向相互作用力。此法向作用力载荷 $F_{n}$ 向下在硅片上产生应力场, 随着切深的增大, 应力场扩展压迫硅片形成凹陷, 形变超出弹性范围及屈服强度时发生塑性变形。此法向反作用力载荷 $F'_{n}$ 向上同样在砂轮微单元上产生应力场, 压迫砂轮微单元形变。切向 $x$ 方向, 砂轮微单元顺着磨削运动轨迹在硅片上以速度 $V$ 滑动, 伴随着法向载荷会产生滑动摩擦力 $f$ , 形成应力场作用于硅片, 使其沿砂轮微单元磨削运动轨迹方向受挤压发生塑性流动生成切屑。同样反作用力 $f'$ 也作用在砂轮微单元上, 使其发生磨损。

2 计算及分析

2.1 法向弹性接触

分解的法向上, 切深较小时, 接触处于弹性阶段, 接触区域为圆形, 根据接触力学中赫兹理论^[9]公式, 可求得接触圆的半径 $a 、$ 对应切深的接触深度 $t_{w}$ 和接触中心点的最大压应力 $p_{0},$ 公式如下:

$\begin{array}{l} a = {(\frac{3 F_{n} R}{4 E^{*}})}^{1 / 3} (1) \\ t_{w} = {(\frac{9 F_{n}^{2}}{16 R E^{* 2}})}^{1 / 3} (2) \\ p_{0} = \frac{3}{2} \frac{F_{n}}{π a^{2}} = {(\frac{6 F_{n} E^{* 2}}{π^{3} R^{2}})}^{1 / 3} (3) \end{array}$

式中: $R$ 为磨粒半径; $E^{*}$ 为等效弹性模量, $\frac{1}{E^{*}} = \frac{1 - ν_{D}^{2}}{E_{D}} + \frac{1 - ν_{w}^{2}}{E_{w}}$ , 其中, $E_{D} 、 E_{w}$ 分别为金刚石和单晶硅的弹性模量, $ν_{D} 、 ν_{w}$ 分别为金刚石和单晶硅的泊松比。

砂轮微单元与硅片接触达到弹性接触极限时, 其临界点就是最大接触压应力 $p_{0}$ 达到硅的屈服强度 $Y$ , 根据式(1)~(3)可求出砂轮微单元与硅片接触时超出硅片弹性接触范围的临界法向载荷、临界切深及临界接触圆半径。

法向载荷接触处于弹性阶段的应力场情况同样依据接触力学的赫兹理论^[9]来得到。如图3所示, 在接触圆内( $r < a), z = 0$ 的硅片表面应力场(三向主应力)的极坐标表达式为:

$\begin{array}{l} \{\begin{array}{l} \frac{σ_{r}}{p_{0}} = \frac{1 - 2 ν_{w}}{3} (\frac{a^{2}}{r^{2}}) [1 - {(1 - \frac{r^{2}}{a^{2}})}^{3 / 2}] - \\ {(1 - \frac{r^{2}}{a^{2}})}^{1 / 2} \\ \frac{σ_{θ}}{p_{0}} = \frac{1 - 2 ν_{w}}{3} (\frac{a^{2}}{r^{2}}) [1 - {(1 - \frac{r^{2}}{a^{2}})}^{3 / 2}] - \\ 2 ν {(1 - \frac{r^{2}}{a^{2}})}^{1 / 2} \\ \frac{σ_{z}}{p_{0}} = - {(1 - \frac{r^{2}}{a^{2}})}^{1 / 2} \end{array} \\ (4) \end{array}$

	Figure Option View Download New Window
	图3 弹性阶段的应力分析Fig.3 Stress analysis in elastic phase

在接触圆外( $r > a$ ), $z = 0$ 的硅片表面应力场的极坐标表达式为:

$\frac{σ_{r}}{p_{0}} = - \frac{σ_{θ}}{p_{0}} = \frac{(1 - 2 ν_{w}) a^{2}}{3 r^{2}} (5)$

在硅片表面以下( $z < 0$ )沿 $z$ 轴的应力分布可认为是在半径 $r$ 上的环形集中力, 即:

$\{\begin{array}{l} \frac{σ_{r}}{p_{0}} = \frac{σ_{θ}}{p_{0}} = - (1 + ν_{w}) [1 - (\frac{z}{a}) \arctan (\frac{a}{z})] + \\ \frac{1}{2} {(1 + \frac{z^{2}}{a^{2}})}^{- 1} \\ \frac{σ_{z}}{p_{0}} = - {(1 + \frac{z^{2}}{a^{2}})}^{- 1} \end{array} (6)$

同时, 主剪切应力 $τ_{1}$ 的分布可以表示为:

$τ_{1} = 0.5 |σ_{z} - σ_{r}| (7)$

由式(4)~(10)可得出接触硅片在弹性接触阶段的应力分布情况如图4所示。

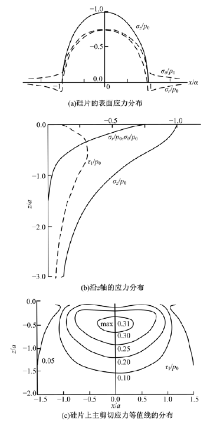	Figure Option View Download New Window
	图4 弹性接触阶段接触硅片的应力分布Fig.4 Stress distribution of contact with silicon wafer during elastic contact phase

法向载荷反作用到砂轮微单元上可看成是以结合剂为基体、金刚石磨粒为表层的双层体受法向力作用的情形, 如图5所示。根据多层体上的接触力学赫兹理论^[9], 可对砂轮微单元进行载荷应力分析。双层体接触力学分析过程中, 设定表层的弹性模量 $E_{1}$ 对应砂轮微单元中金刚石磨粒的弹性模量 $E_{D},$ 表层的厚度为 $h,$ 对应磨粒的直径 $2 R;$ 基体的弹性模量 $E_{2}$ 对应砂轮微单元中结合剂的弹性模量 $E_{J},$ 接触半径为 $a 。$

	Figure Option View Download New Window
	图5 砂轮微单元受载荷看作双层体接触受力示意图Fig.5 Contact force diagram of wheel micro unit load as double body

根据双层体弹性接触理论分析结果给出不同 $E_{1} / E_{2}$ 比值下砂轮微单元等效的应力分布情况, 如图6所示。

	Figure Option View Download New Window
	图6 弹性接触阶段砂轮微单元等效应力分布Fig.6 Elastic contact stage grinding wheel micro unit equivalent stress distribution

由图6可以看出:砂轮微单元双层体在接触表面上的应力分布与作用在硅片接触表面的情况相似, 只是方向相反, 互为作用与反作用力, 而接触表面以下由于是双层体, 虽正应力分布的趋势仍与硅片上的相似, 但由于存在界面, 不同的材料特性(弹性模量及泊松比不同)使得剪应力的传递在界面上出现跳跃或不连续性。

2.2 法向塑性接触

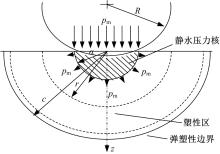
分解的法向上, 切深 $t_{w}$ 超过弹性临界切深后, 接触开始进入塑性阶段, 可根据接触力学^[9]的“ 空腔模型” 理论(见图7)来进行分析。硅片产生的内层位移近似成起始于接触点的放射线, 它的应变等值线是半球形。在这个简化的塑性接触模型中, 磨粒的接触面被包围在半径为 $a$ 的半球“ 静水压力核” 内, 核内有平均接触压力 $p_{m}, p_{m}$ 不会使硅片产生塑性屈服, 但在“ 静水压力核” 之外, 塑性流动向周围扩散, 塑性应变逐渐变小, 直至半径为 $c$ 处的弹性应变, 这是塑性变形的边界, 其中 $c > a 。$

	Figure Option View Download New Window
	图7 塑性压入硅片的空腔模型示意图Fig.7 Schematic diagram of cavity model of plastic pressure in silicon wafer

	Figure Option View Download New Window
	图8 不同载荷下单晶硅单次压痕形貌图Fig.8 Monocrystalline silicon single indentation morphology under different load

在硅片塑性区 $a \leq r \leq c,$ 应力表达式为:

$\{\begin{array}{l} \frac{σ_{r}}{Y} = - 2 \ln (\frac{c}{r}) - \frac{2}{3} \\ \frac{σ_{θ}}{Y} = - 2 \ln (\frac{c}{r}) + \frac{1}{3} \end{array} (8)$

在硅片弹性区 $r \geq c,$ 应力表达式为:

$\{\begin{array}{l} \frac{σ_{r}}{Y} = - \frac{2}{3} {(\frac{c}{r})}^{3} \\ \frac{σ_{θ}}{Y} = \frac{1}{3} {(\frac{c}{r})}^{3} \end{array} (9)$

在静水压力核的边界上, $p_{m}$ 可表达为:

$\frac{p_{m}}{Y} = {(- \frac{σ_{r}}{Y})}_{r = a} = 2 \ln (\frac{c}{a}) + \frac{2}{3} (10)$

而塑性变形边界位置的表达式为:

$(\frac{E^{*}}{Y}) (\frac{a}{R}) = 6 (1 - ν_{w}) {(\frac{c}{a})}^{3} - 4 (1 - 2 ν_{w}) (11)$

将式(11)代入式(10)可得半球核内压力表达式为:

$\begin{array}{l} \frac{p_{m}}{Y} = \frac{F_{n}}{Y π a^{2}} = \\ \frac{2}{3} \{1 + \ln [(\frac{E^{*}}{Y}) (\frac{a}{R}) + 4 (1 - 2 ν_{w}) {[6 (1 - ν_{w})]}^{- 1}]\} \\ (12) \end{array}$

分析式(12)可知, 随着磨粒切入尺寸 $(a / R)$ 的增大, 硅片所受的平均压力也逐渐增大, 同样法向载荷也随之增大, 硅片也会从初始塑性变形逐渐扩展至塑性极限而出现断裂, 即当球核内的最大应力达到硅片的脆性破裂强度时, 就会出现裂纹。

将硅片的脆性破裂强度代入式(12)可得出对应精磨3000#砂轮(对应的磨粒半径 $R$ 约为2 μ m)的微单元与硅片塑性接触产生半球核半径 $a$ 的临界值约1.1 μ m, 临界切深约330 nm, 临界法向载荷约45 mN。与单颗金刚石磨粒的硅片压痕试验^[10]结果(如图10所示, 其压头曲率半径为2 μ m)相吻合, 也说明本文进行的微接触法向弹性及塑性理论分析是有效的。

硅片在受法向载荷作用处于塑性阶段时, 砂轮微单元上的应力作用情况与硅片受法向载荷处弹性阶段的分析相似, 砂轮微单元仍看作是双层体受载荷作用的情形, 只是此阶段的法向载荷变大, 由于金刚石磨粒的屈服强度极高, 较难出现塑性变形, 内部应力分布形式不会变化, 只是应力数值会随之增大, 结合界面上的剪应力同样会随之增大, 这样出现界面破坏的可能性就更高。

2.3 叠加切向接触

宏观滑动摩擦定律为 $f = μ F_{n},$ 其中 $μ$ 为滑动摩擦因数, 它是与载荷、接触面积、滑动速度等条件无关的恒定量, 而在微观滑动接触情况下, 滑动摩擦因数就不再是恒定量, 根据能量耗散机制, 滑动摩擦力 $f$ 可假设为滑动时剪切粘着点产生的粘着摩擦力 $f_{a}$ 和变形产生的形变摩擦力 $f_{d},$ 即 $f = f_{a} + f_{d},$ 这样滑动摩擦因数 $μ$ 也可看成是粘着摩擦因数 $μ_{a}$ 和形变摩擦因数 $μ_{d},$ 即 $μ = μ_{a} + μ_{d} 。$ 当接触切深较小时, 处于弹性接触阶段, 滑动摩擦力主要是由滑动中的粘着效应产生, 根据粘着摩擦机理理论, 粘着摩擦力为:

$f_{a} = μ_{a} F_{n} = A_{z} τ_{a} (13)$

式中: $τ_{a}$ 为硅片抗剪切强度平均值。

将式(1)(2)代入式(13), 得到粘着摩擦因数为:

$μ_{a} = \frac{3 π τ_{a}}{4 E^{*} {(t_{w} / R)}^{1 / 2}} \propto F_{n}^{- 1 / 3} (14)$

由式(14)可分析出, 在弹性接触阶段, 滑动摩擦力随着切深及法向载荷的增大是增大的, 而其粘着摩擦因数是随之减小的。

切深越过弹性临界后, 接触开始进入塑性阶段, 此时滑动摩擦力主要是由犁沟形变产生, 根据形变摩擦机理理论, 形变摩擦力为 $f_{d} = μ_{d} F_{n} 。$

由塑性半球核模型知, 核内有平均接触压力 $p_{m}, 故 F_{n} = p_{m} A_{z}, f_{d} = p_{m} A_{x},$ 可求得形变摩擦因数为:

$\begin{array}{l} μ_{d} = \frac{A_{x}}{A_{z}} = \\ \frac{2}{π} {\{(\frac{R}{a})}^{2} \arcsin (\frac{a}{R}) - {[{(\frac{R}{a})}^{2} - 1]}^{1 / 2}\} (15) \end{array}$

由式(15)可分析出, 在塑性接触阶段, 滑动摩擦力随着切深及法向载荷的增大是增加的, 其形变摩擦因数也是随之增大的。

求出切向上的滑动摩擦力, 与法向载荷叠加合成后作用在硅片上, 其合成载荷在硅片上产生的应力分布情况与法向载荷作用时相似, 仍可采用弹性阶段赫兹理论与塑性阶段空腔模型理论来分析, 只是载荷值有所增大, 方向有所偏转, 应力分布情况与单一法向载荷时类似, 如图9所示。

	Figure Option View Download New Window
	图9 叠加上切向滑动摩擦后硅片应力分布情况Fig.9 Stress distribution of silicon wafer after sliding friction is superimposed

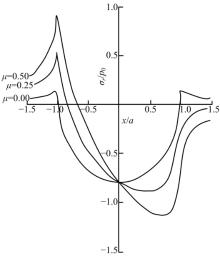
滑动摩擦力作用在砂轮微单元上应力分布的情况与法向载荷作用时的分析相似, 仍要把砂轮微单元看作双层体来分析。由于双层体的材料非均质性且存在界面, 随着弹性模量比值及摩擦因数的增大, 磨粒接触区域的前端出现最大压应力与后端出现最大拉应力的趋势更显著。不同弹性模量比时磨粒接触表面的应力分布如图10所示。

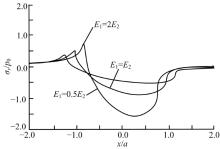	Figure Option View Download New Window
	图10 叠加上切向滑动摩擦后磨粒上应力分布情况Fig.10 Stress distribution of grinding grain after tangential sliding friction is superimposed

分析结果与本文作者所做的微接触仿真分析^[11]结果中切向滑动时硅片和砂轮微单元上的应力分布趋势相一致, 如图11和图12所示, 说明本文进行的微接触叠加切向的理论分析是有效的。

	Figure Option View Download New Window
	图11 硅片上切向滑动仿真的应力云图Fig.11 Stress diagram on silicon wafer during tangential sliding simulation

	Figure Option View Download New Window
	图12 切向滑动仿真砂轮微单元磨粒上的应力云图Fig.12 Stress diagram on grinding grain of wheel micro unit during tangential sliding simulation

3 结论

(1)从硅片自旋转稳定延性域磨削过程中抽取出砂轮微单元与硅片的微接触作为研究对象, 设定假设条件, 提出并建立了微接触的理想三体力学模型。

(2)根据磨削过程, 对力学模型中的接触力进行了分解, 法向上运用接触力学中的赫兹理论与“ 空腔模型” 理论, 将分析获得了硅片上对应弹性和塑性阶段的载荷及应力分布情况, 同时也获得了砂轮微单元上相应的应力分布情况。将分析结果与单颗粒金刚石硅片压痕试验结果进行对比, 证明分析方法有效。

(3)切向上运用微观摩擦学理论分析得出了滑动摩擦力, 叠加合成法向载荷后获得了微接触过程中硅片与砂轮微单元上的应力分布情况。将分析结果与砂轮微单元微接触硅片的仿真结果进行对比, 证明分析方法有效。本文的研究结果可对研究硅片自旋转磨削机理提供相关理论支撑。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Markku T, Teruaki M, Veli-Matti A, et al. Hand book of Silicon based MEMS Materials and Technologies[M]. 2nd ed. London: William Andrew, 2015. [本文引用:1]
[2]	Pei Z J, Strasbaugh A. Fine grinding of silicon wafers[J]. International Journal of Machine Tools and Manufacture, 2001, 41(5): 659-672. [本文引用:1]
[3]	Matsui S. An experimental study on the grinding of silicon wafer-the wafer rotation grinding method[J]. Bull Japan Soc Prec Eng, 1988, 22(4): 295-300. [本文引用:1]
[4]	Zhou L, Tian Y B, Huang H, et al. A study on the diamond grinding of ultra-thin silicon wafers[J]. Journal of Engineering Manufacture, 2012, 226(1): 66-75. [本文引用:1]
[5]	Pei Z J, Fisher G R, Milind B, et al. A grinding-based manufacturing method for silicon wafers: an experimental investigation[J]. International Journal of Machine Tools & Manufacture, 2005, 45(10): 1140-1151. [本文引用:1]
[6]	康仁科, 田业冰, 郭东明, 等. 大直径硅片超精密磨削技术的研究与应用现状[J]. 金刚石与磨料磨具工程, 2003, 136(4): 13-18. Kang Ren-ke, Tian Ye-bing, Guo Dong-ming, et al. Present status of research and application in ultra-precision grinding technology of large-scale silicon wafers[J]. Diamond & Abrasives Engineering, 2003, 136(4): 13-18. [本文引用:1]
[7]	Yan J W, Tooru A, Hirofumi H, et al. Fundamental inverstigation of subsurface damage in single crystalline silicon caused by diamond machining[J]. Precision Engineering, 2009, 33: 378-386. [本文引用:1]
[8]	霍凤伟. 硅片延性域磨削机理研究[D]. 大连: 大连理工大学机械工程学院, 2006. Huo Feng-wei. Study on the mechanism of ductile mode grinding of silicon wafers[D]. Dalian: School of Mechanical Engineering, Dalian University of Technology, 2006. [本文引用:1]
[9]	Johnson K L. Contact Mechanics[M]. London: Cambridge University Press, 1985. [本文引用:4]
[10]	张赜文. 单压头曲率半径对单晶硅和氮化碳薄膜径向纳动损伤的影响[D]. 成都: 西南交通大学机械工程学院, 2010. Zhang Ze-wen. Effect of equivalent radius of indenter on the radial nanofretting damage of monocrystal silicon and α-CN _x film[D]. Chengdu: School of Mechanical Engineering, Southwest Jiaotong University, 2010. [本文引用:1]
[11]	任庆磊, 魏昕, 谢小柱, 等. 硅片自旋转磨削中基于作用力的微观接触仿真研究[J]. 金刚石与磨料磨具工程, 2016, 36(2): 19-23. Ren Qing-lei, Wei Xin, Xie Xiao-zhu, et al. Simulation of micro contact based on interacting force in self rotating grinding of silicon wafer[J]. Diamond & Abrasives Engineering, 2016, 36(2): 19-23. [本文引用:1]

2015

0.0

... 0 引言目前,绝大多数的集成电路(IC)芯片的衬底材料都采用单晶硅片,而单晶硅片的质量直接决定芯片的性能和成品率^[1] ...

2001

0.0

... 300 mm)硅片的加工,而采用超精密磨削加工会比传统加工效益更优,其中应采用杯型金刚石砂轮进行硅片自旋转磨削是典型的硅片超精密磨削加工形式^[2] ...

1988

0.0

... 采用杯型金刚石砂轮进行硅片自旋转磨削加工的方式是由日本学者Matsui首先提出^[3],硅片在真空作用下吸附在旋转工作台上,硅片的直径略小于旋转工作台的直径,两者的中心重合 ...

2012

0.0

... 在硅片自旋转磨削加工的应用过程中,其磨削加工机理是研究的重点,备受国内外研究学者关注^[4] ...

2005

0.0

... 其中,国外代表性的是Pei等^[5]通过改变加工的多因素参数进行了一系列磨削试验,系统研究了磨削加工工艺对硅片表面质量的各种影响 ...

2003

0.0

. 2003, 136(4):13-18

Present status of research and application in ultra-precision grinding technology of large-scale silicon wafers

大直径硅片超精密磨削技术的研究与应用现状

Kang Ren-ke , Tian Ye-bing , Guo Dong-ming

康仁科, 田业冰, 郭东明

... 国内代表性的是康仁科等为获得高质量超薄硅片进行了大量自旋转磨削工艺试验研究^[6] ...

2009

0.0

... 为基础的脆性去除机理及延性域的塑性去除机理^[7],这些机理研究的工作是采用压痕和划痕试验构建经验公式的形式找出硅片的材料去除规律,但由于其磨削过程的复杂性,磨削加工机理研究仍未形成统一的认识 ...

2006

0.0

. 2006, :- DOI:doi:10.7666/d.y965554

Study on the mechanism of ductile mode grinding of silicon wafers

硅片延性域磨削机理研究

Huo Feng-wei

霍凤伟

单晶硅片是制造集成电路时必须采用的衬底材料，在硅片上经过氧化、扩散、沉积、光刻、蚀刻、CMP、多层布线等一系列制程生长出数以亿计的电路器件，然后经过测试、晶片切割/贴片、打线、包装，才能得到一般常见的芯片组件，进而装配到微电子产品上。随着IC制造技术的飞速发展，特征线宽越来越细；为增加芯片产量并降低制造成本，所用的硅片越来越趋向大直径化。为了适应IC制造的要求，对单晶硅抛光片的要求越来越高，包括物理尺寸、平整度、表面粗糙度、纳米形貌、含氧量、晶体完整性和体电阻等指标。为了提高加工质量、降低制造成本，对直径300mm、450mm的硅片的制备需要...

... 同时,硅片材料去除机理研究所依托的微观模型主要是磨粒与硅片间的两体模型,侧重于对磨削中硅片的微观影响研究,欠缺对磨削中砂轮的微观影响研究^[8] ...

1985

0.0

... 1 法向弹性接触分解的法向上,切深较小时,接触处于弹性阶段,接触区域为圆形,根据接触力学中赫兹理论^[9]公式,可求得接触圆的半径 a、对应切深的接触深度 tw和接触中心点的最大压应力 p0,公式如下: ...

... 法向载荷接触处于弹性阶段的应力场情况同样依据接触力学的赫兹理论^[9]来得到 ...

... 根据多层体上的接触力学赫兹理论^[9],可对砂轮微单元进行载荷应力分析 ...

... 2 法向塑性接触分解的法向上,切深 tw超过弹性临界切深后,接触开始进入塑性阶段,可根据接触力学^[9]的#cod#x0201c ...

2010

0.0

. 2010, :- DOI:doi:10.7666/d.y1686995

Effect of equivalent radius of indenter on the radial nanofretting damage of monocrystal silicon and #cod#x003b1;-CN_x film[D]. Chengdu: School of Mechanical Engineering,

单压头曲率半径对单晶硅和氮化碳薄膜径向纳动损伤的影响

Zhang Ze-wen

张赜文

单晶硅是微机电系统(MEMS)的主要结构材料,氮化碳薄膜(α-CNx)和DLC薄膜具有良好的机械性能,作为防护层薄膜已被广泛用于微机电系统。径向纳动广泛存在于MEMS中,对MEMS器件的运行可靠性有重要影响。因此,研究单晶硅的径向纳动损伤及防护不仅可以丰富纳米摩擦学的基础知识,而且对微机电系统的抗纳动损伤设计具有重要的参考价值。本文首先利用纳米压痕仪和2μm球形压头,简要讨论了氮化碳薄膜和单晶硅纳动损伤形式的不同,以及薄膜对基体的保护作用；而后,采用压痕仪和三种典型的不同形状和曲率半径的金刚石压头,研究了压头曲率半径对单晶硅和氮化碳薄膜径向纳动损伤的影响,并结合SEM的损伤形貌观察,分析其接触刚度随循环次数的变化规律。最后,利用纳米划痕仪讨论了划痕实验设定的参数变化对单晶硅和氮化碳薄膜摩擦力和划痕损伤形貌的影响。本文获得的主要结论如下： 1.120nm厚α-CNx薄膜比单晶硅基体软,径向纳动过程中,α-CNx软膜良好的塑性变形能力,对压头的压入产生了一定的缓冲作用,降低了单晶硅基体的损伤,很好的保护了基体。随着循环次数和载荷的增大,单晶硅的损伤形式主要表现为径向裂纹的扩展和剥落,而氮化碳薄膜的损伤依次表现为薄膜弯曲变形、环状裂纹产生和径向裂纹萌生三个阶段。 2.纳动实验中,相对于尖端曲率半径,压头在一定压入深度下的等效曲率半径是决定材料纳动损伤程度的更有效参数。当压入深度小于临界压入深度时,Berkovich压头等效曲率半径最小,对单晶硅和氮化碳薄膜的径向纳动损伤最严重;当压入深度大于临界压入深度以后,2μm球形压头等效曲率半径最小,对单晶硅和氮化碳薄膜的径向纳动损伤最严重。在纳动循环初期,2μm球形压头和Berkovich压头在硅表面的接触刚度升高较快,单晶硅表面的加工硬化现象明显,而20μm球形压头基本不引起硅的加工硬化。 3.在单晶硅和氮化碳薄膜的划痕实验中,划痕速率是影响摩擦力和划痕损伤的主要因素,而加载速率和划痕长度对摩擦力基本没有影响。 4.实验所用DLC薄膜比单晶硅硬度大。薄膜划痕损伤经历三个阶段：薄膜弹性变形、产生鱼骨状裂纹、脆性剥落,分别对应摩擦力曲线的直线段、低斜率上升和急剧增加。同种载荷下,50nm厚薄膜比20nm厚薄膜摩擦力小,损伤小,抗划性能好；同种厚度的CN、薄膜比DLC薄膜抗划性能好。

... 与单颗金刚石磨粒的硅片压痕试验^[10]结果(如图10所示,其压头曲率半径为2 #cod#x003bc ...

2016

0.0

. 2016, 36(2):19-23

Simulation of micro contact based on interacting force in self rotating grinding of silicon wafer

硅片自旋转磨削中基于作用力的微观接触仿真研究

Ren Qing-lei , Wei Xin , Xie Xiao-zhu

任庆磊, 魏昕, 谢小柱

... 分析结果与本文作者所做的微接触仿真分析^[11]结果中切向滑动时硅片和砂轮微单元上的应力分布趋势相一致,如图11和图12所示,说明本文进行的微接触叠加切向的理论分析是有效的 ...