ZPETC方法针对已有的闭环控制环路做了前馈矫正^[8], 设被控的闭环控制环路为:

Gclosed(z-1)=z-dBc(z-1)Ac(z-1)(1)

式中: z-d为闭环系统带来的 d阶滞后; Bc(z-1)和 Ac(z-1)可以分别表示成如下形式:

Bc(z-1)=bc0+bc1z-1+…+bcmz-m, bc0≠0Ac(z-1)=1+ac1z-1+…+acnz-n

针对式(1)所示的闭环控制系统, 加入一个前馈控制器r(k):

r(k)=Ac(z-1)B(z-1)yd(k+d)(2)

式中: yd(k+d)为 d阶的相位超前用以补偿闭环系统引入的 d阶滞后。

设系统的输入为 yin(k), 输出为 yout(k),则:

yout(k)=yin(k)r(k)Gclosed(z-1)(3)

从式(3)可以看出:通过加入前馈控制器 r(k)可以消除闭环控制系统中所有的零点和极点, 使得系统的整体传递函数变成单位1。只要保证初始状态为零, 便可以实现系统输出对输入的完美复现, 达到理想控制的效果。理想控制的控制结构框图如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 理想控制结构示意图Fig.1 Schematic of perfect control structure

理想控制可以达到消除零点和极点, 实现完美输出的目的, 但是当被控对象 Gclosed(z-1)存在单位圆外的零点时, 便不可以直接消除。因为如果直接消除被控对象单位圆外的零点, 会在控制器 r(k)中引入单位圆外的极点, 而单位圆上或者是单位圆外的极点会导致系统震荡或者不稳定。针对这些不可以直接消除的零点, Tomizuka^[4]提出了零相差轨迹控制方法。

针对闭环传递函数分子 Bc(z-1)中部分零点不可以直接消除的情况, 首先把 Bc(z-1)分成两个部分, 具体表示为:

Bc(z-1)=Bca(z-1)Bcu(z-1)(4)

式中: Bca(z-1)为零点位于单位圆内的部分, 可以采用理想控制的方法直接消除; Bcu(z-1)为零点位于单位圆外的部分, 不能直接采用理想控制的方法进行消除^[6]。

根据式(4)对 Bc(z-1)的分解情况, 利用 rk前馈控制器把分子中位于单位圆外的零点消掉。 r(k)的具体表达式为:

r(k)=Ac(z-1)Bca(z)Bcu(1)yd(k+d)(5)

式中: yd(k+d)表示d阶相位超前; Bcu(l)为常数项, 用来归一化前馈控制器的增益。

加入该前馈控制器之后, 输出与输入之间的关系为:

yout(k)=r(k)Gclosed(z-1)yin(k)=[Bcu(z-1)/Bcu(1)]yin(k)(6)

轨迹控制的误差在频率域可以分为幅度误差和相位误差。设输入一个正弦函数为:

yin(k)=asin(ωTk), 0≤ωT≤π(7)

式中: a为输入正弦函数的幅值; T为控制系统的抽样时间。

经过式(5)所示的前馈控制器和闭环系统之后的输出响应为:

yout(k)=aMsin(ωTk+ϕ)(8)

式中: M、ϕ分别为控制系统所带来的幅度增益和相位误差。

把传递函数(式(6))从 Z域变换到频率域:

T(ω)=Bcu(e-jωT)/Bcu(1)(9)

由式(8)(9)可以得出:

M=|Bcu(e-jωT)/Bcu(1)|ϕ=∠Bcu(e-jωT)/Bcu(1)(10)

由于单位圆上和圆外的零点无法利用理想控制理论直接消除, 而这些零点会给系统带来 M倍的幅度增益和 ϕ度的相位误差。在低频段, 上述两个误差值较小, 影响不大, 但是在高频段, 这些误差会对控制系统的控制性能造成很大的影响。尤其是相位滞后, ϕ度的相位滞后量将导致 ϕ/ω秒的时间滞后。因此在不能完全消除掉零点的情况下, 可以尽量消掉零点所带来的相位滞后量, 对提高控制系统性能具有重要意义。

针对上述问题, Tomizuka^[4]提出了零相差控制方法。在式(5)所示的前馈控制器中加入不可消除零点的共轭, 即:

r(k)=Ac(z-1)Bcu(z)Bca(z)[Bcu(1)]2yd(k+d)(11)

此时, 系统总的传递函数变为:

F(z)=[Bcu(z-1)/Bcu(1)][Bcu(z)/Bcu(1)](12)

将其变换到频域为:

[Bcu(e-jωT)/Bcu(1)][Bcu(ejωT)/Bcu(1)]=[Re(ω)-jIm(ω)][Re(ω)+jIm(ω)]=Re(ω)2+Im(ω)2(13)

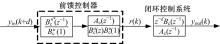
式(12)表示的传递函数没有虚数项, 因此不会引入相位延迟, 解决了不可直接消除零点会带来相位滞后的问题。零相差轨迹控制的控制结构框图如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 零相差控制的结构示意图Fig.2 Schematic of ZPETC structure

通过之前的理论分析可以看出, 零相差控制方法可以有效地抑制闭环控制系统的相位滞后, 提高系统的控制性能。但是这种方法的实现是建立在精确建模的基础之上的。如果建模不精确^{[9, 10, 11]}, 则零相差控制方法的效果将会大打折扣, 甚至出现反作用。为了尽可能地保证零相差控制器的性能, 本文采用白噪声扫频的方法对快速反射镜进行建模。

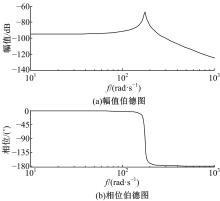
图3为快速反射镜通过白噪声扫频获得的幅频响应和相频响应。从图3可以看出:在幅频曲线中存在一个凸起, 这是由快速反射镜模型中二阶谐振环节引起的。从图3中可以看出:谐振频率约为178 rad/s, 峰值大小为-67.7 dB。相频曲线的第1个相位下降点与幅频曲线的谐振点几乎重合, 下降幅度为180 rad。另外相频曲线在高频段还有一个垂直下降阶段, 下降的幅度比较大, 这部分是扫频时出现的误差, 在建模的时候应该舍去。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 白噪声扫频图Fig.3 Diagram of white noise sweep

利用Matlab中的Matlab System Idengification Toolbox工具箱结合上面的扫频获得数据对快速反射镜进行拟合建模, 拟合出的快速反射镜模型形式为:

M=ks2+αs+β(14)

式中: k、α、β为待定的模型参数, 结合白噪声扫频获得的数据可以初步确定参数。

通过Matlab System Idengification Toolbox工具箱拟合出的模型还是一个比较粗糙的模型, 并不能很好地与扫频获得的响应曲线相符。此时, 在这个原始模型的基础上手动修改各个参数并让其伯德图尽可能地与扫频曲线重合, 达到精准建模的目的。通过这种方法确定出3个参数分别为: k=0.5593, α=7.428, β=31500,并画出其伯德图如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 快速反射镜模型伯德图Fig.4 Bode chart of FSM model

通过对比白噪声扫频获得的频响曲线和拟合出模型的频响曲线可以看出:①两幅图的谐振频率基本相同, 分别为190和178 rad/s; ②两幅图的谐振峰值分别为-66.4和-67.7 dB, 基本相同; ③两幅图的相位拐点分别为147.3 rad/s和149 rad/s, 基本重合。总的来说, 本文模型基本上复现了快速反射镜的性能曲线, 可以作为后续控制器设计的模型依据。

图5为加入零相差前馈控制器的快速反射镜控制结构框图。图中后半部分是依据白噪声扫频方法建立的模型, 以及根据模型设计的PID闭环控制器。前半部分则是根据闭环控制结构设计出的零相差前馈控制器。从图5中可以看出:零相差前馈控制器包含两个部分:①前馈控制器的被控对象中可以直接消除零极点的部分; ②不可以直接消除零极点需要消除相位差的部分。将前馈控制器的输出 r(k)作为后续闭环控制的输入, 与反馈信号作差, 并直接给到PI控制器。为了仿真传感器所引入的噪声对控制系统的影响, 在反馈环路中加入了幅值为0.002的白噪声。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 快速反射镜控制结构框图Fig.5 FSM control block diagram

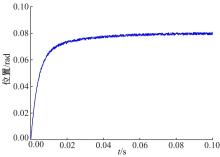
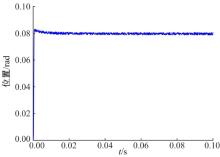
图6和图7分别为单纯PID控制下和PID结合ZPETC下快速反射镜的阶跃响应曲线。输入的阶跃信号的响应时间为0 s、终值为0.08 s, 扰动幅值为0.002。通过对比两幅图可以获得两种控制策略的性能差异如表1所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 单纯PID控制下快速反射镜的阶跃响应Fig.6 Step response of FSM under PI control

表1

Table 1

表1(Table 1)

表1 PID控制和零相差控制的阶跃响应性能比较 Table 1 Comparison of step response performance between PID control and ZPETC 控制方法 响应时间/ms 超调量 稳态误差 PID控制 60 0 0.002 PID结合零相差控制 8 0.0015 0.002

表1 PID控制和零相差控制的阶跃响应性能比较 Table 1 Comparison of step response performance between PID control and ZPETC

结合图6、图7和表1可以看出:加入零相差前馈控制器之后, 快速反射镜的性能获得很大提升。从阶跃响应上来看, 结合零相差控制方法的输出曲线在保持稳态误差不变的基础上, 响应时间变得更短, 响应速度获得大幅度提高, 提升了快速反射镜的控制精度和快速性。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 PID和ZPETC下快速反射镜的阶跃响应Fig.7 Step response of FSM under ZPETC and PI contol

为了测试引入零相差控制器以后系统的响应速度, 进行阶跃响应试验。给定的阶跃信号终值为0.08 s, 分别采集获得单纯PI控制和ZPETC控制下响应曲线如图9所示。分析图9中的曲线可以得到两种控制方法的一些关键性能指标, 整理如表2所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 PI和ZPETC下阶跃响应对比曲线Fig.9 Contrast step response curve of FSM under ZPETC and PI contol

表2

Table 2

表2(Table 2)

表2 PID控制和零相差控制的阶跃响应性能比较 Table 2 Comparison of step response performance between PID control and ZPETC 控制方法 响应时间/ms 超调量 稳态误差 PID控制 50 0 0.003 PID结合零相差控制 12 0 0.003

表2 PID控制和零相差控制的阶跃响应性能比较 Table 2 Comparison of step response performance between PID control and ZPETC

观测图9和表2可以看出:引入ZPETC方法以后, 快速反射镜的阶跃响应时间由原来的50 ms降低到12 ms, 响应速度提高了4倍多, 证明零相差控制方法有助于提高快速反射镜的响应速度。但是通过对比表1和表2可以看出, 仿真结果与实际试验结果存在偏差。零相差控制器的响应时间相比于仿真结果有所增加, 另外零相差控制方法所带来的超调量消失, 两种控制方法的稳态误差也都有所增加。零相差控制方法比仿真结果的响应时间更长是由建模误差引起的, 在试验过程中, 通过不断改进模型可使实际的阶跃响应结果越来越接近理想的仿真结果。图10给出了模型精校前、后的阶跃响应对比曲线, 从图中可以清楚地看到前面所述的趋势。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 被控模型矫正前、后阶跃响应对比曲线Fig.10 Contrast step response curve of FSM under original and corrected model

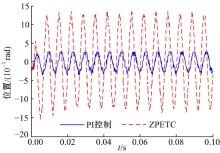
为了测试两种控制方法的高频响应特性, 进行正弦响应试验。输入的正弦信号幅值为0.01, 频率为150 Hz。分别获得两种控制方法下输出曲线如图11所示。从图11中可以看出:单纯PI控制下的快速反射镜对于150 Hz的输入, 输出衰减特别厉害, 只能复现输入的25%左右, 衰减幅度达到75%。而加入零相差控制以后, 输出基本复现了输入, 只是由于建模误差的原因产生了微小的超调。从图11中还可以看出:单纯PI控制下, 快速反射镜的输出相位滞后比较大, 而引入零相差控制器以后相位滞后量有所减小。这一点在第1节零相差控制原理中已经提到, 零相差控制器的引入会消除被控对象中的相位差。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 PI和ZPETC下正弦响应对比曲线Fig.11 Contrast sinusodial response curve of FSM under ZPETC and PI control