引用本文
刘杰, 张平, 高万夫. 基于条件相关的特征选择方法[J].吉林大学学报（工学版）, 2018,48(3): 874-881
LIU Jie, ZHANG Ping, GAO Wan-fu. Feature selection method based on conditional relevance[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 874-881  
Doi:10.13229/j.cnki.jdxbgxb20170231
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有 吉林大学学报编辑部
基于条件相关的特征选择方法
刘杰1,2, 张平2,3, 高万夫1
1.吉林大学 计算机科学与技术学院,长春 130012
2.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012
3.吉林大学 软件学院,长春 130012

作者简介:刘杰(1973-),女,副教授,博士.研究方向:数据挖掘.E-mail:liu_jie@jlu.edu.cn

基金:国家自然科学基金项目(61502199).
摘要

在特征选择中候选特征与类标签的相关性是随着已选特征的加入而动态变化的,本文提出了一种新的相关性定义——条件相关性,即基于每一个已选特征给出候选特征和类标签新的相关性定义。利用条件相关性,提出了一种新颖的基于信息论的条件相关特征选择算法(CRFS)。首先,在理论上证明了条件相关性的优越性;然后,将新的特征选择算法在2个不同的分类器和10个真实数据集上与7种特征选择算法进行比较。实验结果表明,新的算法能有效提高分类性能。

关键词: 人工智能; 特征选择; 信息论; 条件相关性; 分类
中图分类号:TP301 文献标志码:A 文章编号:1671-5497(2018)03-0874-08
Feature selection method based on conditional relevance
LIU Jie1,2, ZHANG Ping2,3, GAO Wan-fu1
1.College of Computer Science and Technology,Jilin University,Changchun 130012,China
2.Symbol Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun 130012,China
3.College of Software,Jilin University,Changchun 130012,China
Abstract

In feature selection, with the increasing number of selected features, the relevance between candidate features and class labels is dynamically changed. This paper presents a new definition of relevance, called Conditional Relevance (CR). That is, we give a new definition of the relevance between candidate features and class labels when each selected feature is given. Consequently, we propose a novel Conditional Relevance Feature Selection (CRFS) method based on information theory. First, the superiority of the CR is verified in theory. Then, the new feature selection algorithm is compared with seven feature selection algorithms on two different classifies and on 10 real data sets. The results show the highest accuracy and the average highest accuracy of the 10 data sets on two classifiers. Experimental results show that the new algorithm can effectively improve the classification performance.

Keyword: artificial intelligence; feature selection; information theory; conditional relevance; classification
0 引 言

随着大数据时代的到来, 各种各样类型的数据信息呈现指数级增长。如何快速、准确地从庞杂的信息中选择出最有价值的信息变得越来越重要。降维技术就是解决这一类问题的重要手段。目前主要的降维技术主要包括特征提取和特征选择两种[1]。特征提取就是将原有的高维数据转换为低维数据, 改变了原始特征的物理意义; 特征选择则是从原有的高维数据中挑选出最有价值的特征, 保留原始特征的物理特性。在简单用于找出那些有价值的特征时, 两种降维技术作用是一样的, 但如果研究者想要分析所选出来的特征的实际意义, 那么, 特征选择方法更优越, 它可以更好地帮助研究者分析所选出来的特征的潜在意义。

根据选择策略的不同, 特征选择算法一般分为封装法(Wrapper)、嵌入法(Embedded)和过滤法(Filter)3类[2]。封装法是依赖于分类器的一种方法, 它一般分为两步:①选出一个特征子集; ②评估这个子集的分类表现。重复步骤①和②直到选出合适的子集。封装法分类表现一般比较好, 但缺点是太过依赖具体的分类器容易出现过拟合, 并且执行效率较低。嵌入法是将特征选择集成在学习机训练过程中, 通过优化一个目标函数, 在训练分类器的过程中实现特征选择。嵌入法相对于封装法执行效率较高, 但是构造一个合适的函数优化模型往往比较困难。相比较而言, 过滤法是效率最高的一种选择策略, 它独立于任何分类器, 并且具有较好的泛化能力, 因此应用广泛, 尤其是基于信息论的过滤法。对于特征子集的搜索策略, 一般分为启发式搜索、随机搜索和完全搜索3种[4, 5]。本文使用的是启发式搜索策略中的序列向前搜索方法。

基于信息论的特征选择算法是当前的研究热点。传统的基于互信息的特征选择算法都将候选特征与类标签的互信息值作为相关项, 例如mRMR[6], 但它们却忽略了候选特征与类标签的相关性是随着已选特征的加入而动态改变的。本文将候选特征与类标签在已知已选特征下的条件互信息作为相关项, 去掉那些与已选特征冗余关系强烈的候选特征, 选出最有意义的特征。为证明本文提出的相关性概念— — 条件相关性, 比传统的相关性优越, 接下来给出理论说明。另外, 在10个真实数据集上分别对本文条件相关特征选择(Conditional relevance feature selection, CRFS)算法与其他7种特征选择算法进行比较, 其中JMI[7]与本文算法的框架相似, mRMR、CIFE[8]、DISR[9]和ICAP[10]都是特征选择领域的经典算法, FIM[11]和IWFS[12]分别是2013年和2015年提出的算法。这8种特征选择算法都是基于信息论的过滤特征选择算法, 它们不依赖于具体的分类器, 利用2个经典的分类器(1近邻(1NN)和朴素贝叶斯(NB))对它们进行分类表现测试, 并给出实验效果图和选出来的最高准确率, 最后对8种算法在10个数据集上的运行时间进行对比。

1 信息论的一些基本概念

假设X, Y和Z是3个n维的离散随机变量, X={x1, x2, …, xn}, Y={y1, y2, …, yn}, Z={z1, z2, …, zn}。信息熵的定义如下[13, 14, 15, 16]:

H(X)=-∑i=1np(xi)logp(xi)(1)

式中:p(xi)为随机事件xi发生的概率。

变量的不确定性越大, 熵就越大, 所提供的信息量也就越大。联合信息熵的定义如下:

H(X, Y)=-∑i, jp(xi, yj)logp(xi, yj)(2)

式中:p(xi, yj)=p(X=xi, Y=yj)。

式(2)表示随机变量X和Y同时发生的不确定性大小。条件熵的定义如下:

H(X|Y)=-∑i∑jp(xi|yj)p(yj)logp(xi|yj)(3)

式(3)表示在联合随机变量集XY中, 所有X|Y是否发生的平均不确定的大小。

相对熵的定义如下:

D(P|Q)=∑i=1nP(xi)logP(xi)Q(xi)(4)

由相对熵的概念可以定义平均互信息为[15]:

I(X; Y)=∑i∑jp(xi, yj)logp(xi, yj)p(xi)p(yj)(5)

式(5)为互信息的定义, 由定义可知互信息可以表示为熵的形式, 具体如下:

I(X; Y)=H(Y)-H(Y|X)(6)I(X; Y)=H(X)-H(X|Y)(7)I(X; Y)=H(X)+H(Y)-H(X, Y)(8)

根据式(6)~(8)可知:平均互信息可以理解为两个随机变量之间的关联程度, 即给定一个随机变量后, 对另一个随机变量不确定性的削弱程度。因而互信息取值最小为0, 意味着给定一个随机变量对确定另一个随机变量没有帮助, 即两个随机变量相互独立; 最大取值为随机变量的熵, 意味着给定一个随机变量, 能完全消除另一个随机变量的不确定性。类似于条件熵, 条件互信息用相对熵表示如下:

I(X; Y|Z)=DP(xi, yj, zk)|P(yj|zk)P(zk)(9)

式(9)也可以写成如下形式:

I(X; Y|Z)=∑i∑j∑kp(xi, yj, zk)logp(xi, yj|zk)p(xi|zk)p(yj|zk)(10)

条件互信息可以表示成熵的形式, 具体如下:

I(X; Y|Z)=H(X|Z)-H(X|YZ)(11)I(X; Y|Z)=H(XZ)+H(YZ)-H(XYZ)-H(Z)(12)

其中, 熵、条件熵、互信息、条件互信息的值均大于等于零。

2 条件相关特征选择方法
2.1 条件相关性

特征选择的目标是从高维特征中选出那些与类标签最相关的一个特征子集。传统的基于信息论的特征选择算法认为候选特征与类标签的互信息值越大代表该候选特征越重要。它们把候选特征的选择过程看成一个个独立的事件, 而事实上, 候选特征与类标签的相关性是随着已选特征的加入而不断改变的。

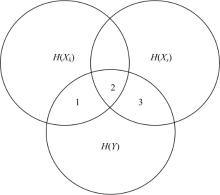
图1中, Xk为候选特征, Xs为已选特征, Y为类标签。传统的相关性是候选特征与类标签的互信息I(Xk; Y), 即图1中的1+2部分, 然而, 从图1中可以看出, 由于2部分在之前选择已选特征Xs的过程中已经计算过, 即它同时属于候选特征和已选特征与类标签的相关性, 所以它是候选特征与已选特征对于类标签的冗余部分; 条件相关性是指图1中的1部分, 将它定义为候选特征与类标签的相关性, 用条件互信息表示, 即I(Xk; Y|Xs)。从图1中可以看出:1部分代表候选特征与类标签真正的相关性, 有效避免了2部分产生的冗余作用。由于在特征选择的过程中, 已选特征的个数不断增多, 为考虑到所有已选特征与候选特征的冗余关系, 本文提出全新的条件相关性CMI, 用候选特征与类标签在每一个已选特征条件下的条件互信息之和表示:

CMI(Xk; Y|S)=∑Xj∈SI(Xk; Y|Xj)(13)

图1 H(Xk), H(Xs), H(Y)关系图Fig.1 Relationship of H(Xk), H(Xs) and H(Y)

式中:S为已选特征集。

下面用一个例子形象地说明条件相关性与传统相关性相比所具有的优势。

如表1所示, 其中Oi(i=1, 2, …, 6)为样例, Xk(k=1, 2, …, 7)为特征, Y为类标签。分别用条件相关性和传统的相关性对表1的例子进行特征选择。条件相关性是动态变化的, 即式(13), 传统的相关性为I(Xk; Y), 下面根据表1分别计算两种相关性。执行过程如下所示。

表1 样例及类标签 Table 1 Samples and classes

(1)当k=1时, 计算所有特征与类标签的互信息:

I(X1; Y)=0.0817; I(X2; Y)=0.0817

I(X3; Y)=0.0817; I(X4; Y)=0.1909

I(X5; Y)=0.1909; I(X6; Y)=0.0000

I(X7; Y)=0.4591

由以上比较I(Xi; Y), 第1个被选出来的特征为X7, 此时已选特征集S={X7}, 候选特征集为{X1, X2, X3, X4, X5, X6}; 此时, 条件相关性与传统相关性选择的特征一样, 都是X7。

(2)当k=2时, 计算候选特征在已选特征集下的条件互信息:

CMI(X1; Y|S)=0.0817

CMI(X2; Y|S)=0.0817

CMI(X3; Y|S)=0.2075

CMI(X4; Y|S)=0.7771× 10-15

CMI(X5; Y|S)=0.0817

CMI(X6; Y|S)=0.2075

由以上比较CMI(Xi; Y|S), 第2个被选出来的特征为X3, 而传统的相关性算法选择的是X4, 此时已选特征集S={X7, X3}, 候选特征集为{X1, X2, X4, X5, X6}。

(3)当k=3时, 计算候选特征在已选特征集下的条件互信息:

CMI(X1; Y|S)=0.3333

CMI(X2; Y|S)=0.6667

CMI(X4; Y|S)=0.1258

CMI(X5; Y|S)=0.2075

CMI(X6; Y|S)=0.4591

由以上比较CMI(Xi; Y|S), 第3个被选出来的特征为X2, 而传统的相关性算法选择的是X5, 此时已选特征集S={X7, X3, X2}。由传统的相关性选择的特征集合为S'={X7, X4, X5}。

分析以上执行过程可以看出:选择第一个特征时, 通过步骤(1)的计算, 利用条件相关性和传统相关性均选择与类标签最相关的特征X7, 即与Y互信息的最大值。在选择第2个特征时, 按传统相关性选择X4, 而利用条件相关性则选择X3。虽然I(X4; Y)> I(X3; Y), 但是此时已选特征集S中已有X7, 所以需要考虑X4和X3在已选特征X7的影响下与Y的相关性。通过计算I(X4; X7)=0.3167, I(X3; X7)=0.1110× 10-15≈ 0可知I(X4; X7)> I(X3; X7), 即X4与X7的相关性大于X3与X7的相关性, 而计算I(X4; Y|X7)=0.7771× 10-15≈ 0, I(X3; Y|X7)=0.2075, 说明X4在已选特征X7的影响下, 几乎没有为分类提供新的信息并且与X7有较高的相关性, 实质上表明X4为冗余特征, 其提供了与X7相似的信息; 而I(X3; Y|X7)> I(X3; Y), 说明X3在X7的影响下为分类提供了更多信息。在选择第3个特征时, 同样需要考虑已选特征集的影响, 有效剔除冗余特征, 从而选择提供更多分类信息的特征。

至此, 条件相关性选择出来的特征集合可以有效地对样例进行分类, 这个集合称为最佳特征子集。而利用传统相关性并没有选择出最佳特征子集。所以, 通过图1的分析和表1的例子可以看出, 条件相关性与传统的相关性相比具有更好的分类效果。根据条件相关性的特点, 本文提出一种条件相关的特征选择算法CRFS。

2.2 条件相关特征选择方法

由于条件相关性的计算与传统的相关性不同, 它并不是将候选特征的选择过程看成一个个独立的事件, 而是基于每一个已选特征动态变化的。根据其这一特点本文设计了一个全新的特征选择算法:

Xk=∑Xs∈S(I(Xk; Y|Xs)-I(Xk; Xs))(14)

对于每一个候选特征依次计算式(14), 将获得的最大值对应的候选特征加入到S中, 迭代此过程直到满足规定的特征数目。具体执行过程的伪代码如下所示。

输入:原始特征集F, 类标签Y, 阈值K

输出:选择的特征对应索引集S

① S=⌀

② Maxs =⌀

③ k = 0

④ for each Xk∈ F

⑤ 根据式(6)计算 I(Xk ; Y)

⑥ end for

⑦ S(1) = argmax( I(Xk ; Y) )

⑧ Xs=F[S(1)]

⑨ F = F - {S(1)}

⑩ k = k+1

⑪ while k< K

⑫ for each Xk∈ F

⑬ 根据式(11)(6)计算

R(Xk)=I(Xk; Y | Xs) - I(Xk; Xs)

⑭ Maxs(Xk) = Maxs(Xk) + R(Xk)

⑮ end for

⑯ S(k) = argmax( Maxs(Xk) )

⑰ Xs=F[S(k)]

⑱ F = F - {S(k)}

⑲ k = k + 1

①~③行是初始化过程, 将要选择的特征个数k设为0, 临时存放候选特征最大值的一个变量Maxs设为空, 将要选择的特征集合S设为空; ④~⑥行, 是算法选择第一个特征, 计算在原始特征集合F中的每一个特征与类标签的互信息, 选择互信息最大的特征作为第一个已选特征; ⑦~⑲行, 依次选择每一个使得式(14)最大的特征, 然后将该特征加入已选集合S中, 不断重复此过程, 直到k达到阈值。

3 实验结果及分析

在10个真实数据集上对条件相关特征选择算法进行实验, 具体数据集描述如表2所示[17]。对于这些数据集, 将特征子集数目限制在30个。实验给出这10个数据集在两个分类器1近邻(1NN)和朴素贝叶斯(NB)上平均准确率效果图, 以及这8个特征选择算法在10个数据集上达到的最高平均准确率。

表2 数据集描述 Table 2 Description of datasets

表2中:PCMAC是文本数据; warpPIE10P和Yale属于人脸图像数据; lung、colon、Prostate_GE、GLIOMA、CLL_SUB_111、SMK_CAN_187和GLI_85为生物学数据。从表2和以上描述可以看出:实验数据来源广泛, 并且数据既有多分类又有二分类。除了PCMAC和colon是离散的, 其他数据集均是连续的。离散数据可以使特征选择算法更有效, 所以在本文中采用Akadi等[10]的离散方法, 将所有连续数据离散化。

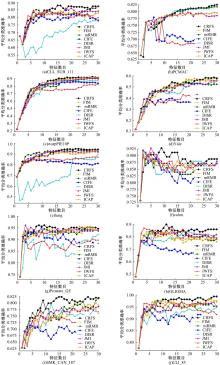
针对这10个真实数据集, 分别对7个生物数据集采用留一法验证, 因为它们都属于数据样例较少, 而特征数维度较高的数据结构, 其他3个数据集采用10次十折交叉验证法。对这10个数据集利用1近邻和朴素贝叶斯两种分类器进行分类, 计算两个分类器的平均准确率, 实验效果如图2所示。

图2 10个数据集在分类器上的准确率Fig.2 Accuracy of classifier achieved with 10 data sets

从图2可以看出:条件相关特征选择算法取得了不错的分类效果。为了进一步证实本文算法的优势, 表3列出了8种算法在10个数据集上执行2个分类器获得的最高平均准确率, 其中黑色加粗数值代表8种特征选择算法中取得的最高平均准确率的最大值。

表3 8种算法在分类器上的最高平均准确率比较 Table 3 Comparison of highest average accuracy of 8 algorithms on classifiers %

从表3可以看出:在两个分类器的分类下, 本文算法在10个数据集中的最高平均准确率均取得最高, 其中在colon和Prostate_GE两个数据集上与JMI同时取得最高, 在最后一行显示的10个数据集的平均准确率上, 8种特征选择算法的平均最高准确率分别是87.67%, 85.61%, 85.59%, 79.96%, 83.52%, 85.35%, 81.68%和85.20%。可以看出, 条件相关特征选择算法有明显优势。

对CRFS算法的时间复杂度进行讨论:假设选择的特征数目为n, 数据集总的特征数目为N, 那么CRFS算法的时间复杂度为O(n× N)。事实上进行比较的其他7种算法的时间复杂度也均为O(n× N)。但由于各种算法使用的评价函数不同, 导致函数值的求解效率有所差别, 这将直接影响对于同一数据集各种算法的执行时间。8种算法在10个数据集上的具体运行时间如表4所示。本次实验在Python2.7环境下运行, 电脑硬件设备配置如下:处理器为Intel(R) Core(TM)2 Quad CPU 安装内存4.00 GB。对于CRFS、FIM、mRMR、CIFE、JMI、ICAP算法的评价函数均使用互信息、条件互信息或联合互信息的线性组合, 这些算法的执行时间差别较小, 且较IWFS和DISR运行时间较短。IWFS的评价函数使用乘法的形式, 并在计算权重过程中引入了熵, 增加了计算时间。DISR的评价函数使用除法的形式, 并使用了计算较复杂的3个变量联合熵H(Xk, Xs, Y), 所以DISR是执行效率最低的一种算法。

表4 8种算法在10个数据集上的运行时间比较 Table 4 Comparison of run time of 8 algorithms on 10 data sets s

综上, 通过与其他7种算法的分类准确率和算法执行时间的比较可以看出, 本文CRFS算法取得了不错的效果。

4 结束语

本文提出了一种新的基于条件相关性概念的条件相关特征选择CRFS算法, 首先在理论和实验上说明了条件相关性与传统的相关性相比有一定的优势; 然后用CRFS算法与其他7种特征选择算法FIM, mRMR, CIFE, DISR, JMI, IWFS和ICAP在10个真实数据集上进行了对比实验。实验结果表明, CRFS算法具有一定的优势。然而, 由于数据特征维数的不断增加, 数据间的关系变得越来越复杂, 如何客观、快速地找出数据间真实的关系仍是一项艰巨而紧迫的任务。在未来的研究工作中, 将对不同类型的数据进行划分, 给出具体适用于某一类数据的特征选择算法。

The authors have declared that no competing interests exist.

参考文献
[1] Bennasar M, Hicks Y, Setchi R. Feature selection using joint mutual information maximisation[J]. Expert Systems with Applications, 2015, 42(22): 8520-8532. [本文引用:1]
[2] Zhao Z, Morstatter F, Sharma S, et al. Advancing feature selection research-ASU feature selection repository[J/OL]. [2017-03-02]. http: ∥eprints. kku. edu. sa/65/1/ZhaoEtAl. pdf. [本文引用:1]
[3] Bolón-Canedo V, Sánchez-Maroño N, Alonso-Betanzos A, et al. A review of microarray datasets and applied feature selection methods[J]. Information Sciences, 2014, 282(5): 111-135. [本文引用:1]
[4] 刘元宁, 王刚, 朱晓冬, 等. 基于自适应多种群遗传算法的特征选择[J]. 吉林大学学报: 工学版, 2011, 41(6): 1690-1693.
Liu Yuan-ning, Wang Gang, Zhu Xiao-dong, et al. Feature selection based on adaptive multi-population genetic algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(6): 1690-1693. [本文引用:1]
[5] 姚登举, 杨静, 詹晓娟. 基于随机森林的特征选择算法[J]. 吉林大学学报: 工学版, 2014, 44(1): 137-141.
Yao Deng-ju, Yang Jing, Zhan Xiao-juan. Feature selection algorithm based on rand om forest[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(1): 137-141. [本文引用:1]
[6] Peng H C, Long F H, Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238. [本文引用:1]
[7] Yang H H, Moody J. Data visualization and feature selection: new algorithms for nongaussian data[J]. Advances in Neural Information Processing Systems, 1999, 12: 687-693. [本文引用:1]
[8] Lin D, Tang X. Conditional infomax learning: an integrated framework for feature extraction and fusion[C]∥European Conference on Computer Vision, Graz, Austria, 2006: 68-82. [本文引用:1]
[9] Meyer P E, Schretter C, Bontempi G. Information-theoretic feature selection in microarray data using variable complementarity[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(3): 261-274. [本文引用:1]
[10] Akadi A E, Ouardighi A E, Aboutajdine D. A powerful feature selection approach based on mutual information[J]. International Journal of Computer Science & Network Security, 2008, 8(4): 116-121. [本文引用:2]
[11] Bennasar M, Setchi R, Hicks Y. Feature interaction maximisation[J]. Pattern Recognition Letters, 2013, 34(14): 1630-1635. [本文引用:1]
[12] Zeng Z, Zhang H, Zhang R, et al. A novel feature selection method considering feature interaction[J]. Pattern Recognition, 2015, 48(8): 2656-2666. [本文引用:1]
[13] 石峰, 莫忠息. 信息论基础[M]. 3版. 武汉: 武汉大学出版社, 2014: 14-52. [本文引用:1]
[14] 赵晓群. 信息论基础及应用[M]. 北京: 机械工业出版社, 2015: 27-53. [本文引用:1]
[15] Zhao Juan, Zhou Yi-wei, Zhang Xiu-jun, et al. Part mutual information for quantifying direct associations in networks[J]. Proceedings of the National Academy of Sciences, 2016, 113(18): 5130-5135. [本文引用:2]
[16] Schreiber T. Measuring information transport[J/OL]. [2017-03-06]. http:∥citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.35.3215&rep=rep1&type=pdf. [本文引用:1]
[17] Li J D, Cheng K W, Wang S H, et al. Feature selection: a data perspective[J/OL]. [2017-03-06]. https: ∥arxiv. org/pdf/1601. 07996. pdf. [本文引用:1]