定义1 对于任意序列, 其对应的最小字长的二进制序列为原序列的CSNB序列。

例:若序列为1, 3, 2, 6, 5, 4, 则CSNB序列为001, 011, 010, 110, 101, 100。

定义2 任意1到n的全排列序列, 通过式(1)计算得到的二进制数为此序列的奇偶校验码CSNB_c:

CSNBc=∑i=1n10i-1×CSNBi⊕(1)

式中:N􀱇表示在二进制数N中每位依次求异或所得到的值; CSNB_i为CSNB序列中的第i个数。

例:若序列为1, 3, 2, 6, 5, 4, CSNB序列为001, 011, 010, 110, 101, 100, 则奇偶校验码的计算过程为:

001⊕=1; 011⊕=0; 010⊕=1; 110⊕=0; 101⊕=0; 100⊕=1

CSNB_c为100101。

定义3 任意CSNB序列, 通过式(2)计算所得的值为CSNB序列的前序错位求和部分CSNF。

CSNF=∑i=1n10i-1×CSNBi(2)

定义4 任意CSNB序列, 通过式(3)计算所得的值为CSNB序列的后序错位求和部分CSNA。

CSNA=∑i=1n10n-i×CSNBi(3)

任意长度为n的CSNB序列, 其CSNF和CSNA的长度均为$n+\lfloor log_2 n \rfloor + 1$。

定义5 任意CSNB序列, 通过式(4)计算所得的值为CSNB序列的CSNB。

$CSNB = 10^{\lfloor log_{10} n \rfloor + 10_n + 1} \times CSNF + \\ 10^{n} \times CSNA +CSNB_{c} \quad (4)$

因为CSNB序列为二进制序列, 所以式(4)为二进制计算。

例:CSNB序列为:001, 011, 010, 110, 101, 100

CSNB=$10^{\lfloor log_{10} n \rfloor +10_{n}+1}$× CSNF+

10ⁿ× CSNA+CSNB_c=10¹¹¹¹×

(10⁰× 1+10¹× 11+10¹⁰× 10+

10¹¹× 110+10¹⁰⁰× 101+10¹⁰¹× 100)+

10¹¹⁰× (10⁰× 100+10¹× 101+10¹⁰× 110+

10¹¹× 10+10¹⁰⁰× 11+10¹⁰¹× 1)+

100101=10000111110000110100101

原序列以十进制的方式记录排序序列。计算机对十进制数常用的编码方式是BCD码, 以16位计算机为例, 在记录十进制数时计算机会为每个十进制数预留16位。而CSNB序列是以二进制的方式记录排序序列, 计算机在记录时不需要编码转换。其对比结果如表1所示。

表1

Table 1

表1(Table 1)

表1 原序列与CSNB序列的比较 Table 1 Comparison of original sequence and sequence CSNB 比较项目 CSN序列 CSNB序列 计算机存储二 进制数(n=16) 4=0000 0000 0000 0100 15=0000 0000 0001 0101 4=00100 15=01111 序列的长度为n时, 需要的存储空间/bit 16n n($\lfloor$log2n $\rfloor$+1)

表1 原序列与CSNB序列的比较 Table 1 Comparison of original sequence and sequence CSNB

原序列、CSNB序列以及CSNB都具有记录序列的功能, 其空间复杂度对比结果如表2所示(计算机为k位)。

表2

Table 2

表2(Table 2)

表2 CSN序列、CSNB序列以及CSNB占用空间对比 Table 2 CSN sequence, CSNB sequence and CSNB space comparison bit 序列 长度 CSN序列 kn CSNB序列 n($\lfloor$log2n$\rfloor$+1) CSNB 2$\lfloor$log2n$\rfloor$+3n+2 n≤ 8 n($\lfloor$log2n$\rfloor$+1)≤ 2$\lfloor$log2n$\rfloor$+3n+2< kn 8< n< 2k 2$\lfloor$log2n$\rfloor$+3n+2< n($\lfloor$log2n$\rfloor$+1)≤ kn

表2 CSN序列、CSNB序列以及CSNB占用空间对比 Table 2 CSN sequence, CSNB sequence and CSNB space comparison bit

由表2可知, 当序列长度n≤ 8时, CSNB序列较CSNB有更好的空间利用率, 且CSNB序列并没有进行改装压缩, 所以也不需要繁琐的解压过程, 但当8< n< 2^k时, CSNB则需要更少的空间, 且适用范围远比CSNB序列要大。

为尝试所有的排序可能, 需要建立一个具有 Ann个叶子节点的完全平衡树, 进而通过深度优先遍历找到所有结果节点。但当n> 3时, 有多个结果节点, 所以需要奇偶校验码CSNB_c来验证每个结果的正确性。并且, 决策树过于庞大, 需要对其进行剪枝。剪枝过程可以在遍历的过程中通过末尾数(01校验码)来判断, 进而对于错误的节点可以尽早删除掉。

定义6 如果一个节点N的奇偶校验码为N􀱇¹, 其祖先节点要求的奇偶校验码为1, 且N􀱇¹≠ 1, 则剪枝发生在该节点之上, 此时, 称该剪枝过程为奇剪枝。

定义7 如果一个节点N的奇偶校验码为N􀱇¹, 其祖先节点要求的奇偶校验码为0, 且N􀱇¹≠ 0, 则剪枝发生在该节点之上, 此时, 称该剪枝过程为偶剪枝。

定义8 如果一个在第n层(根节点为第0层)的节点N与回溯到根节点中所有遍历到的节点进行式(3)的计算, 得到结果的倒数第n位为C, 其祖先节点要求的01校验码为1, 且C≠ 1, 则剪枝发生在该节点之上, 此时, 称该剪枝过程为1剪枝。

定义9 如果一个在第n层(根节点为第0层)的节点N与回溯到根节点中所有遍历到的节点进行式(3)的计算, 得到结果的倒数第n位为C, 其祖先节点要求的01校验码为0, 且C≠ 0, 则剪枝发生在该节点之上, 此时, 称该剪枝过程为0剪枝。

因为任意CSNB都满足:当i≠ j时, CSN_i≠ CSN_j且1≤ CSN_i≤ n, 所以, 任意一个在第n层的节点向下遍历的所有兄弟节点中, 其奇偶校验值N􀱇¹为0和1是等可能的, 其通过回溯计算和的倒数第n位为0和1也是等可能的。决策树在没有剪枝时一共有 Ann+ ∑i=0nAni个节点, 所以通过上述4种剪枝计算方法可知, 剪枝后的决策树中的节点为 Ann+∑i=0nAni/4ⁿ。

性质1 由于奇偶剪枝不需要累加运算, 且在选定下一节点时可直接计算, 并且奇偶剪枝针对的是真实的排序值, 所以奇偶剪枝较01剪枝速度更快、效率更高。

虽然通过决策树的剪枝方法能够删掉大多数非解节点, 但剪枝后的决策树仍然可能存在多个所在层为n的叶子节点, 所以还需要通过CSNA对所有可能解进行检验。

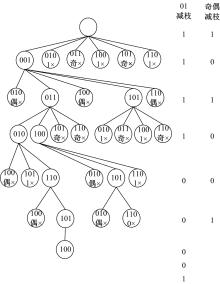
例:CSNB序列为:001, 011, 010, 110, 101, 100, CSNB=100001111100101, 其剪枝策略如图1所示, 先进行奇偶校验, 再进行01校验。其中, “ 奇× ” 、“ 偶× ” 、“ 1× ” 和“ 0× ” 分别表示进行奇剪枝、偶剪枝、1剪枝和0剪枝操作。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 剪枝策略示意图Fig.1 Pruning strategy schematic

创建决策树是从逻辑的角度分析算法的执行过程, 本质上解压算法并不需要构建决策树。决策树在选择节点时, 是通过剪枝策略来判断其选择的节点是否正确, 从逻辑角度来说, 是尝试着确定CSNB_i的位置。

根据式(2)求CSNB_i, 本质上是在求以CSNB₁, CSNB₂, …, CSNB_n为未知数, 方程CSNF=2⁰× CSNB₁+2¹× CSNB₂+…+2^n-1× CSNB_n(方程为十进制方程)的解, 其中当i≠ j时, CSN_i≠ CSN_j且1≤ CSN_i≤ n。

而决策树是在明确CSNB_i值的情况下, 去求其位置, 即为求以x₁, x₂, …, x_n为未知数, 方程CSNF= 2x1× CSNB₁+ 2x2× CSNB₂+…+ 2xn× CSNB_n(方程为十进制)的解, 其中当i≠ j时, x_i≠ x_j且1≤ x_i≤ n-1。

根据以上分析, 可制定CSNB解压算法的步骤如下所示。

(1)建立记录所有未知数状态的未知数状态表(State table), 所有未知数的初始状态是Uncertain。若未知数个数为n, 则未知数的其他可能状态数为[1, n]中的整数。

(2)从State table中提取一个未被测试过的且状态为Uncertain的未知数, 并执行第(3)步。如果不存在符合条件的未知数, 则执行第(5)步。

(3)将选定的未知数依次通过奇偶检验和01检验, 如果都通过, 则执行第(4)步; 否则, 将此未知数视为已检测状态, 并执行第(2)步。

(4)将选定的未知数的初始状态更改为未被选定的状态中最小的状态数, 将其他状态为Uncertain的未知数均视为未被测试状态, 执行第(2)步。

(5)若State table中仍存在状态为Uncertain的未知数, 则将状态数最大的未知数以及之后的未知数状态设定为Uncertain, 将之后的未知数视为未检测状态, 并继续执行第(2)步; 否则执行第(6)步。

(6)通过CSNA判断找到的可能解的正确性, 若正确, 算法结束; 否则, 将状态数最大的未知数以及之后的未知数状态设定为Uncertain, 将之后的未知数视为未检测状态, 并执行第(2)步。

所谓正向检验, 就是给定任意排列的CSNB, 由CSNB解其原序列, 若解唯一, 不仅能说明CSNB系统的正确性, 还能检验解压算法的正确性。

任意长度为n的CSNB序列, 其全排列的总数为n!, 当n=9时, 一共有9!=362880种排列情况, 一一测试是不合理的, 所以当1< n< 9时, 对全排列进行测试; 当n≥ 9时, 随机生成1000个排序序列, 并对其进行检验。检验包括没有奇偶校验、没有CSNA校验以及所有校验均存在这3种情况, 01校验本身属于解方程过程, 所以不能没有, 检验结果如表3所示。

表3

Table 3

表3(Table 3)

表3 正向检验解的唯一性 Table 3 Positive test uniqueness of the solution 长度 没有奇偶校验 没有CSNA校验 全校验 n=1, 2, 3, 4 有唯一解 有唯一解 有唯 一解 n=5 均有唯一解 有3个CSNB, 有两 个解, 多解率为2.5% n=6 有12个CSNB, 有两 个解, 多解率为1.67% 有52个CSNB, 有多 个解, 多解率为7% n=7 有192个CSNB, 有多 个解, 多解率为3.8% 有1121个CSNB, 有多 个解, 多解率为22% n=8 有3074个CSNB, 有多 个解, 多解率为7.6% 有15312个CSNB, 有 多个解, 多解率为38% n=9 多解率为12.8% 多解率为56% 没有 唯一解

表3 正向检验解的唯一性 Table 3 Positive test uniqueness of the solution

由表3可知, CSNA的查错率更高。假设没有奇偶校验和没有CSNA校验的多解率符合某种概率分布, 且是相互独立的, 则当5< n< 9的全校验的多解率应该大于零, 但测试结果显示全校验的多解率为0, 所以可知, 没有奇偶校验与没有CSNA校验的多解率的概率是相关的。

所谓反向检验, 就是给定任意排列的CSNB, 计算是否存在一个不同的CSNB序列的CSNB与其相同, 若存在则解不唯一; 若不存在则解唯一。通过对比正向检验和反向检验的结果可知解压算法的正确性。

任意长度为n的CSNB序列, 其全排列的总数为n!, 通过与其所有不同的CSNB序列作对比, 其比较次数为n!!。当n=9时, 一共有9!!=362880!次比较, 这样测试是不合理的, 所以采用与正向检验相同的方法对其进行反向检验, 即当1< n< 9时, 对全排列进行测试, 当n≥ 9时, 随机生成1000个排序序列, 并对其进行检验。检验结果如表4所示。

表4

Table 4

表4(Table 4)

表4 反向检验解的唯一性 Table 4 Uniqueness of the solution of reverse test 长度 没有奇偶校验 没有CSNA校验 全校验 n=1, 2, …, 8 与正向检验结果相同 n=9 均有唯一解 n=10 均有唯一解 n=11 均有唯一解 n=12 均有唯一解

表4 反向检验解的唯一性 Table 4 Uniqueness of the solution of reverse test