位图局部敏感哈希的匹配二进制特征搜索算法

引用本文

杨东升, 张展, 廉梦佳, 王丽娜. 位图局部敏感哈希的匹配二进制特征搜索算法[J].吉林大学学报（工学版）, 2018,48(3): 893-902
YANG Dong-sheng, ZHANG Zhan, LIAN Meng-jia, WANG Li-na. Matching binary feature search algorithm of bitmap locality sensitive hashing[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 893-902 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170299
Permissions

位图局部敏感哈希的匹配二进制特征搜索算法

杨东升¹, 张展^1,², 廉梦佳^1,², 王丽娜^1,²

1.中国科学院沈阳计算技术研究所,沈阳 110168

2.中国科学院大学,北京 100049

作者简介:杨东升(1965-),男,研究员,博士生导师.研究方向:数控技术,机器人视觉.E-mail:dsyang@sict.ac.cn

基金:“核高基”国家科技重大专项项目(2017ZX01030-201).

摘要

针对现有匹配二进制特征搜索算法效率低和入围点少的问题,提出了快速计算位图算法和位图局部敏感哈希算法。首先,计算左图提取的二进制特征的位向量;然后,使用快速计算位图算法计算位向量的位图,将位图作为关键字,并与二进制特征的标识作为映射,构建局部敏感哈希表;接着,将哈希表中的关键字存入位集;最后,判断右图提取的二进制特征对应的位图是否存在于哈希表中,优化查询哈希表中的匹配二进制特征,提高匹配二进制特征的搜索效率和质量。实验证明:位图局部敏感哈希算法提高了二进制特征近邻搜索的效率、增加了入围点数。

关键词: 计算机应用; 位图; 局部敏感哈希; 二进制特征; 图像匹配; 汉明距离

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2018)03-0893-10

Matching binary feature search algorithm of bitmap locality sensitive hashing

YANG Dong-sheng¹, ZHANG Zhan^1,², LIAN Meng-jia^1,², WANG Li-na^1,²

1.Shenyang Institute of Computing Technology, Chinese Academy of Science, Shenyang 110168,China

2.University of Chinese Academy of Science, Beijing 100049,China

Abstract

To solve the issues of low efficiency and less inliers of existing matching binary feature search algorithms, a Fast Calculating Bit Map algorithm (FCBM) and a Bit Map Locality Sensitive Hashing algorithm (BMLSH) are proposed. First, the bit vectors of the binary features extracted from left image is calculated and the FCBM is used to calculate bitmap of each bit vector. Second, the bitmaps of the bit vectors are taken as the key words, and each keyword and its corresponding binary feature identifier are used to construct local sensitive hash table, then the maps are stored in the hash table. Furthermore, the keywords in the hash table are stored in the bit set. Finally, the bit set is used to judge whether the bitmaps of right image binary feature exists or not in the hash table, and the query of matching binary features are optimized to improve the search efficiency and quality. Experiments show that the proposed BMLSH can improve the search efficiency and increase the number of inlier points.

Keyword: computer application; bitmap; locality sensitive hashing; binary feature; image matching; hamming distance

文章图片

0 引言

二进制特征是图像特征匹配和识别的先进技术, 相对于SIFT^{[1, 2]}和SURF^{[3, 4]}特征, 其具有有效计算、快速比较和紧密存储的优点。目前, 主要二进制特征的提取算法有BRIEF^[5]、ORB^[6]、BRISK^[7]、FREAK^[8]和CBD^[9]等。二进制特征即01字符串, 一般使用汉明距离和最近邻比率算法^[10](NNDR)判断两个二进制特征是否匹配。

搜索匹配特征向量的算法有多种, 但并不适用于搜索匹配二进制特征, 因此有人提出了适用于搜索匹配二进制特征的哈希技术。例如:Indyk等^[11]提出基于哈希表的近似近邻搜索算法— — 局部敏感哈希(LSH)算法, 其只适用于欧氏空间特征向量的搜索。Lv等^[12]提出多探头局部敏感哈希(MPLSH), 有效地解决了高维特征的相似度搜索问题, 且可用于匹配二进制特征搜索。Kong等^[13]提出将曼哈顿哈希表用于大规模图像检索, 把二进制特征转化为十进制数, 根据曼哈顿距离计算不相似度进行查询。Shrivastave等^[14]通过旋转致密化位排列哈希, 实现了高维二进制特征的快速近邻搜索。Lin等^[15]提出在高维数据中使用决策树快速监督哈希算法。Liong等^[16]提出了基于紧凑二进制代码学习的深度哈希算法。Lin等^[17]提出了二进制哈希编码的深度学习算法, 实现了图像的快速检索。Norouzi等^[18]在紧凑二进制代码中, 给出最小亏损哈希算法; 之后, 采用多索引实现了在汉明空间的二进制代码子字符串的快速搜索, 使在汉明空间的k近邻(KNN)搜索成为可能^[19]。Muja等^[20]在使用自动算法配置的快速近邻搜索中, 给出多个随机KD树算法搜索高维匹配特征, 在二进制特征快速匹配算法中提出了多层次聚类树(HCT)算法, 在高维数据可扩展近邻算法^[21]中, 对近似最近邻算法做出总结, 并给出相应的近似近邻快速搜索的函数库(FLANN)。文献[22]提出了位图索引的近邻搜索算法, 具有占用空间少和搜索速度快的优点。

本文提出了快速计算位图(FCBM)算法和位图局部敏感哈希(BMLSH)算法, 搜索两个数据集中的匹配二进制特征或相似的二进制代码, 以提高匹配特征搜索效率和增加入围点数。本文实验使用文献[23]给出的图像数据集提取的ORB二进制特征, 使用入围点数、入围率、平均查询时间、平均投影误差和空间复杂度等评价标准, 将本文算法与FLANN函数库中的二进制特征匹配算法(包括LINEAR、MPLSH和HCT等)进行对比。实验结果表明:在相同条件下, 本文算法的消耗时间少、搜索到的入围点数多、匹配入围率与平均投影误差与其他算法接近、消耗的内存空间与多探头局部敏感哈希算法相当。

1 理论基础

1.1 二进制特征

二进制特征的提取^{[5, 24, 25]}是根据特征点邻域中, 对应的“ 点对” 之间灰度值大小确定特征0、1状态的取值, 如式(1)所示:

$T (P_{a}) = \{\begin{array}{l} 1, if I (p_{a}^{r 1}) - I (p_{a}^{r 2}) > 0 \\ 0, otherwise \end{array} (1)$

式中: $P_{a}$ 为特征点邻域的点对; $I (P_{a}^{r 1})$ 和 $I (p_{a}^{r 2})$ 分别为特征点邻域中点对 $P_{a}$ 的前一个和后一个采样像素的灰度值; $T (P_{a})$ 为比较 $I (P_{a}^{r 1})$ 和 $I (p_{a}^{r 2})$ 得到的只有0、1两个状态的单位长度的二进制字符串。

设 $L$ 为二进制特征的长度, $F$ 代表二进制特征, 是依次将多个 $T (P_{a})$ 按顺序移位算出的整型数, 如式(2)所示:

$F = \sum_{0 \leq a < L} 2^{a} T (P_{a}) (2)$

二进制特征(如BRIEF、ORB、BRISK和FREAK特征)在存储时, 依次将每8个 $T (P_{a})$ 作为一个无符号字符类型(uchar, 8 bit)存入内存, 每个二进制特征长度为L, 则每个二进制特征可以用L/8个无符号字符型表示。

1.2 局部敏感哈希

最初的局部敏感哈希算法^[11], 需要将欧氏空间中的特征向量转换到汉明空间中, 同时确定特征向量在哈希表中的位置, 而二进制特征一般是由BRIEF、ORB等算法直接提取^{[26, 27]}。局部敏感哈希的核心是点积: $h (\vec{v}) = \vec{v} \cdot \vec{x},$ 其中 $\vec{v}$ 为查询高维空间点的特征向量, $\vec{x}$ 为使用高斯分布生成的维数相同的特征向量。存储点积到哈希表中的思路是:近邻的特征向量散列到同一个哈希桶中, 哈希函数如式(3)所示:

$h^{x, b}(\vec{v}) = \lfloor \frac{\vec{x}· \vec{v}+b}{w} \rfloor \quad (3)$

式中: $\lfloor$· $\rfloor$为向下取整函数; $w$ 为每个划分容器的宽度; $b 为 0 到 w$ 之间的随机变量, 其作用是使量化错误更容易分析。

点积的投影使近邻特征映射到哈希表中相同的位置, 需要的条件如下:

(1)在 $R^{d}$ 空间( $d$ 维欧氏空间)中, 任意特征向量 $p$ 和 $q$ 之间的距离小于等于 $R_{1}$ , 则特征向量 $p$ 和 $q$ 被分到同一个哈希桶的概率 $P_{H}$ 大于等于 $p_{1}$ , 如下所示:

$\begin{array}{l} P_{H} = [h (p) = h (q)] \geq p_{1} \\ for ‖ p - q ‖ \leq R_{1} \end{array} (4)$

式中: $‖•‖$ 为 $L_{2}$ 范数。

(2)在 $R^{d}$ 空间, 任意特征向量 $p$ 和 $q$ 之间的距离大于等于 $R_{2}$ , 则特征向量 $p$ 和 $q$ 被分到同一个哈希桶的概率 $P_{H}$ 很小, 小于等于 $p_{2}$ , 且 $p_{2} < p_{1}$ , 如下所示:

$\begin{array}{l} P_{H} = [h (p) = h (q)] \leq p_{2} \\ for ‖ p - q ‖ \geq c R_{1} = R_{2} \end{array} (5)$

注意, 由于线性点积, 两特征向量 $p$ 和 $q$ 所在哈希桶的距离 $‖ h (p) - h (q) ‖$ 拥有的量级分布与 $‖ p - q ‖$ 成比例, 因此 $p_{1} > p_{2} 。$

1.3 位图索引

位图索引 $V$ 是一个长度为 $N$ 的聚集位向量^[22], 每位的状态只能是0或1。在位向量V中第 $i$ 位的状态, 取决于对应的记录, 如果该位置的记录是t, 则该位为1; 否则为0。举例说明:当前的文件中, 有6个记录, 每条记录是(int, binary)的点对, 编号为1到6, 并依次为:(30, 101), (30, 010), (40, 011), (50, 101), (40, 010), (30, 011)。

例子中, 有6条点对记录, 所以位向量长度为6, 第1条、第2条和第6条的整型记录为30, 所以整型记录30对应的位向量为110001; 同理, 整型记录40和50对应的位向量分别为001010和000100。例子中, 第1条和第4条的二进制记录为101, 所以二进制记录101对应的位向量为100100; 同理, 二进制记录010和011对应的位向量分别为010010和001001。

2 位图局部敏感哈希

2.1 计算二进制特征的位图

二进制特征是高维的位向量, 比如BRIEF、ORB特征是256位, BRISK、FREAK特征为512位。本文以ORB二进制特征为例, 描述本文FCBM算法。ORB特征以无符号字符型(uchar)的形式存储在内存, 所以256位的ORB特征在内存中存储了32个无符号字符型数。FCBM算法的主要目的是让近邻的二进制特征获得相同的或近邻的位图, 并使计算位图的速度更快。

FCBM算法如下:首先从一个无符号字符型数(8 bit)中选取5 bit, 组成一个5 bit的无符号字符类型数 $S_{i}, S_{i} \in [0, 31],$ 则长度为32个无符号类型的ORB特征, 经过以上处理可以得到32个 $S_{i}$ , 将 $S_{i}$ 按照ORB特征中对应无符号类型数的排序, 依次编号为1~32, 则每个ORB特征对应的记录为 $S = S_{1} S_{2} \dots S_{32}; S_{i} \in [0, 31]$ , 即 $S$ 的每个位置上的记录 $S_{i} \in [0, 31] 。$ 然后, 按照1.3节的方法计算位图, 记录0~31都有一个对应的位向量设为

$B_{j}, j \in [0, 31]$ , 将位向量 $B_{j}$ 转化为32 bit无符号整型数, 存储于内存中。最后, 将近邻记录的位向量按位或得到最终位向量作为ORB二进制特征的位图。ORB特征由32个无符号字符型组成, 只取前4个对FCBM算法进行举例说明。

首先, 计算并记录 $S_{i}$ 。如表1所示, $U_{1}$ 和 $U_{2}$ 为两个近邻二进制特征的前4个uchar组成的数据; $M$ 为取位用的4个uchar组成的掩码; $S_{i}$ 是取位的最终结果, $i \in [1, 4]$ , 表示二进制特征的第 $i$ 个uchar。取位是指取特征的uchar类型对应二进制数在掩码为1时的位置的状态(其他位置抹去), 组成的一个新的5 bit数, 掩码 $M$ 的每个uchar类型对应的二进制数中有且只有5个1。如表1所示, 掩码 $M$ 的第一个uchar类型转为二进制数的左起第1、3、5、7、8位为1, 所以取 $U_{1}$ 的左起第1、3、5、7、8位得到的 $S_{1}$ 为00000, 转化为十进制为0; 同理, 取 $U_{2}$ 的第1、3、5、7、8位得到的 $S'_{1}$ 为01000, 转化为十进制为8; 二进制字符串 $S_{1} = 00000$ 与 $S'_{1} = 01000,$ 按位异或结果为01000, 结果中有一个1, 所以二进制字符串 $S_{1}$ 与 $S'_{1}$ 之间的汉明距离为1, 二进制字符串 $S'_{1}$ 是 $S_{1}$ 的1近邻。同理, 获得的 $S'_{2}$ 等于 $S_{2}, S'_{3}$ 是 $S_{3}$ 的二近邻, $S'_{4}$ 等于 $S_{4}$ 。由 $S'_{1}$ 与 $S_{1} 、 S'_{2}$ 与 $S_{2}$ 取位的过程可知, 掩码 $M$ 的主要作用是计算位图时避开近邻二进制特征中的不一样的位, 降低二进制特征向量的维数。

表1 无符号字符型的取位 Table 1 Getting bits of unsigned characters

$M$	10101011	01101011	10101101	11011001
U₁	01010100	10101000	01100001	01010010
$S_{i}$	00000	01100	01001	01100
$U_{2}$	01110100	10101100	11100101	01010010
$S'_{i}$	01000	01100	11011	01100

表1 无符号字符型的取位 Table 1 Getting bits of unsigned characters

由于uchar类型数值的范围为[0, 255], 而uchar类型掩码 $M$ 中有且只有5个1, 从掩码 $M$ 中的8 bit选5 bit设置为1有56种方法。根据掩码取位计算记录 $S_{i},$ 可以事先将这些取位结果算好, 保存在56× 2⁸的数组中, 取位计算记录时不需要移位运算, 而是直接取数组中对应的数据, 这样可以提高计算二进制特征对应位图的效率。然后, 按照章节1.3的方法, 计算位向量:记录

$S_{i}$ 为0至31, 都有一个对应的位向量设为 $B_{j}, j \in [0, 31],$ 表2为 $U_{1}$ 和 $U_{2}$ 取位后所得记录 $S_{i}$ 与 $S'_{i}$ 对应的位向量。

表2 记录S_i和S'_i对应的位向量 Table 2 Bit vector of S_i and S'_i

$U_{1}$		$U_{2}$
记录 $S_{i}$	位图	记录 $S'_{i}$	位图
0	1000	8	1000
9	0010	12	0101
12	0101	27	0010
其他	0000	其他	0000

表2 记录S_i和S'_i对应的位向量 Table 2 Bit vector of S_i and S'_i

最后, 将近邻记录的位向量按位取“ 或” , 其结果作为二进制特征的位图。计算二进制特征时, 位的状态可能跳变, 由0变1或由1变0, 导致近邻记录的位向量是同一位向量或者近邻向量, 如表1近邻记录 $S'_{1}$ 和 $S_{1}$ 的位向量是同一位向量, 近邻记录 $S'_{3}$ 和 $S_{3}$ 的位向量是近邻位向量。

2.2 哈希表构建和位集优化查询

将每个二进制特征的位图或其位图的一部分作为关键字, 将关键字与二进制特征的ID作为映射存入每个哈希表相应的桶中。每个哈希表都有一个与关键字长度一致的掩码, 目的是再计算二进制特征的位图时, 避开近邻特征中不一样的位和降维。一般构建多个哈希表, 哈希表中的一个哈希桶对应一个关键字, 一个关键字对应一个或者多个二进制特征ID。因为ORB二进制特征是由256位组成, 即32个uchar类型, 所以ORB二进制特征位图是32维的位向量, 转化成32 bit的无符号整型数, 保存在内存中。

位集(bitset)是快速查询关键字是否存在的一种算法。本文使用位集对匹配二进制特征的查询进行优化, 以快速判断当前查询特征是否存在于哈希表中。初始化位集为0, 首先根据式(6)将哈希表中所有的关键字key存储到位集bitset[]中, 如下所示:

$bitset [key / 32] | = (1 < < (key% 32)) (6)$

查询时, 根据式(7)判断当前查询关键字是否存在于哈希表中:

$\begin{array}{l} bitset [key / 32] (1 < < (key% 32))! = 0 \\ (7) \end{array}$

若当前计算结果为0, 则关键字不存在; 若计算结果不为0, 说明关键字存在, 则查询与当前哈希表对应的桶。

2.3 保存查询信息与特征匹配判断

在位集中, 若当前关键字存在于哈希表中, 则查询关键字对应的哈希桶中所有ID相应的二进制特征, 计算当前关键字相应的二进制特征与ID相应二进制特征的汉明距离, 当遇到与当前查询二进制特征的最近邻特征和次近邻特征时, 保存相应的ID以及最近邻和次近邻距离。设最近邻距离为d₁, 次近邻距离为d₂, 根据NNDR算法, 判断当前查询特征与ID相应的二进制特征是否匹配, 如式(8)所示:

$R = d_{1} / d_{2} (8)$

若满足阈值条件R< 0.6, 则匹配; 否则不匹配。

3 实验验证

3.1 实验设计

实验包括5个部分:①计算位图:提取左、右两图像的二进制特征, 使用FCBM算法, 分段依次计算每个二进制特征对应的位图。②构建哈希表:使用左图二进制特征对应位图作为关键字, 将关键字与二进制特征的ID作为映射, 存入每个哈希表里相应的桶中, 一个关键字可以对应多个二进制特征的ID。③位集优化搜索:将哈希表中的关键字存到位集中, 原因是位集可以快速判断当前查询关键字是否存在于当前哈希表中。④保存查询信息:若右图特征对应关键字存在于哈希表中, 则计算左图关键字对应二进制特征与当前右图特征的汉明距离, 保存当前特征的最近邻和次近邻距离以及关键字对应特征的ID。⑤匹配入围点判断:使用NNDR算法, 判断左、右两图二进制特征是否匹配, 根据左、右图像匹配点集合, 计算左图转到右图点的旋转矩阵, 旋转矩阵乘以左图点得到的坐标与对应右图点坐标的距离叫投影误差, 根据投影误差判断当前点是否是入围点, 入围点数除以匹配点数即为匹配入围率。

实验使用Windows7操作系统, OPENCV图像处理函数库; 使用文献[23]给出图像数据集所提取的ORB二进制特征作为算法评价数据集。文献[23]给出的图像数据集中, 每个图库有6幅图像, 且每个图库里的图像都是同一场景在不同情况下拍摄的。实验时使用其中的5个图库, 包括bike、boat、luven、trees和ubc图库, 同一图库将第1幅图像提取的ORB特征作为训练特征, 其他图像提取的ORB特征作为匹配查询二进制特征, 图库中每张图提取的ORB特征数如表3所示。使用搜索算法, 查询左图与右图的匹配二进制特征, 计算两图的匹配点数、入围点数、入围率和平均投影误差等。将本文算法与FLANN函数库中的搜索匹配二进制特征的算法进行对比, 包括LINEAR、MPLSH和HCT算法等。

表3 提取不同数据集中各图像的ORB特征个数 Table 3 Number of ORB features for extracting each image in different dataset

3.2 实验数据及对比分析

3.2.1 哈希表数目不同

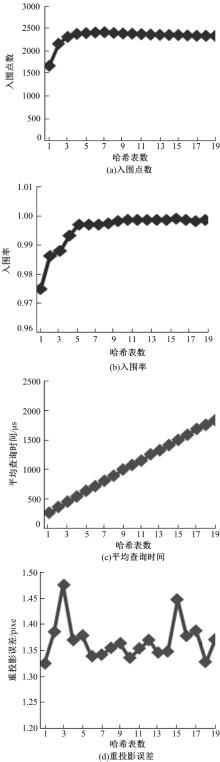
本文BMLSH算法有两个变量, 分别是哈希表数和关键字长度。如图1所示, 本文算法的定量分析图, 设置关键字长度为20, 提取bike图库中bike1图的ORB特征为5972个, bike2图的ORB特征为5067个。由图1(a)可以看出:本文算法搜索到的入围点数在哈希表数不少于3个时, 入围点数大于2300, 并且随着表数的增加, 入围点数先是快速增加随后趋于稳定; 由图1(b)可以看出:本文算法的入围率高, 入围率随着哈希表数的增加先是增加随后趋于稳定; 由图1(c)可以看出:本文算法的平均查询时间随着哈希表数的增加呈线性增长; 由图1(d)可以看出, 本文算法搜索到入围点的平均投影误差小于1.5 pixel。

	Figure Option View Download New Window
	图1 不同哈希表数量时本文算法的性能Fig.1 Performance of proposed method under different number of hash tables

3.2.2 关键字长度不同

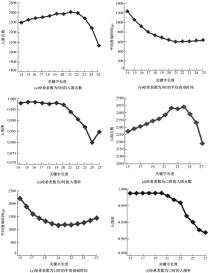
图2为不同关键字长度时本文算法的性能, 定量设置哈希表数为5和12, 提取bike图库中bike1图的ORB特征为5972个, bike2图的ORB特征为5067个。由于3.2.1节入围点数入围率在哈希表数为5时接近最大, 在哈希表数为12时趋于稳定, 所以设置两个定量分析:当哈希表数为5时, 设置关键字长度为14~25; 当哈希表数为12时, 设置关键字长度为15~27。

	Figure Option View Download New Window
	图2 不同关键字长度时本文算法的性能Fig.2 Performance of proposed method under different length of key

由图2(a)(b)(c)可知:随着关键字长度的增加, 入围点数先增加后减小, 入围率逐渐减少, 平均查找时间逐渐减少, 在关键字长度为20左右时, 入围点数最多, 入围率最高, 平均查询时间适中; 由图2(d)(e)(f)可知:随着关键字长度的增加, 入围点数先增加后减小, 入围率逐渐减少, 平均查询时间逐渐减少, 在关键字长度为20左右时, 入围点数最多, 入围率最高, 平均查询时间适中。

3.2.3 不同算法性能的对比

图3为LINEAR、MPLSH和HCT算法, 与本文BMLSH算法的性能对比。其中, 提取bike图库中6张图像的ORB特征数, 如表3所示。本文以bike1作为源图像提取ORB特征作为训练特征, 其他图像(bike2、bike3、bike4、bike5和bike6)提取的ORB特征作为查询特征, bike图库中的图像随着编号的增加其模糊程度也增加。在相同的情况下, 图3(a)表明本文算法的入围点数比其他算法多40个以上; 图3(b)表明, 随着查询特征的增加, 本文算法所需查询时间的增加程度小, 所需的查询时间少; 图3(c)表明本文算法的查询入围率大于95.8%, 与其他算法相当; 图3(d)表明本文算法平均投影误差与其他算法接近。

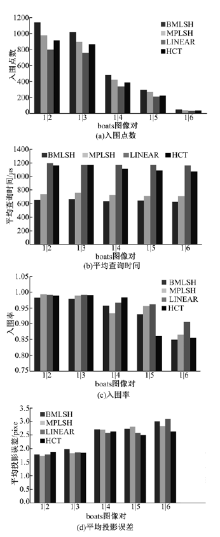
	Figure Option View Download New Window
	图3 使用bike图库时不同算法的性能Fig.3 Performance of different algorithms test bike dataset

图4为使用boat图库, 不同算法的性能对比。提取boat图库中6张图像的ORB特征数, 如表3所示。boat1~boat6图像是不同视角不同旋转角度下拍摄的图像。在相同的情况下, 图4(a)表明本文算法的入围点数多比其他算法至少多11个; 图4(b)表明, 在查询特征数目一定时, 本文算法所需查询时间少且稳定, 为622.899~664.01 μ s; 图4(c)表明本文算法的查询入围率大于85%, 与其他算法相当; 图4(d)表明本文算法平均投影误差与其他算法接近。

	Figure Option View Download New Window
	图4 使用boat图库时不同算法的性能Fig.4 Performance of different algorithms test boat dataset

3.2.4 特征匹配效果对比

图5为本文BMLSH算法与其他算法的入围点连线效果图。实验使用boat图库, 提取boat1和boat2图像的ORB特征分别为1500和1497个。本文BMLSH算法搜索到的入围点数为330个, MPLSH算法搜到295个, LINEAR算法搜到239个, HCT算法搜索到267个。比较入围点连线图5(a)与图5(b)(c)(d)可知, 本文BMLSH算法的入围点连线比较稠密, 匹配入围点数较多。

	Figure Option View Download New Window
	图5 不同算法的入围点连线图Fig.5 Inliers connection diagram of different algorithms

表4为不同算法使用luven图库查询匹配特征的入围点数, 1|2是指luven1和luven2组成的图像对。表5为不同算法使用luven图库查询匹配特征的平均查询时间。由表5可知:本文BMLSH算法查询的入围点数多, 比其他算法多9个以上, 平均查询时间短, 在666.046 μ s以下。表6为不同算法使用trees图库查询匹配特征的入围点数。表7是不同算法使用trees图库查询匹配特征的平均查询时间。由表7可知:本文BMLSH算法的查询入围点数多, 平均查询时间最短, 在636.796 μ s以下。

表4 luven 图库不同算法的入围点数 Table 4 Number of inliers for different algorithms under luven dataset

表5 luven图库不同算法的平均查询时间 Table 5 Average query time by different algorithms under luven dataset μ s

表6 trees图库不同算法的入围点数 Table 6 Number of inliers for different algorithms under trees dataset

表7 trees图库不同算法的平均查询时间 Table 7 Average query time by different algorithms under trees dataset μ s

4 结束语

针对线性搜索、层次聚类树等查询匹配二进制特征时, 效率低和入围点数少的问题, 本文提出了快速计算位图(FCBM)算法以及位图局部敏感哈希(BMLSH)算法。本文算法可用于匹配二进制特征的搜索、二进制特征识别、图像定位和拼接等领域。实验证明:在相同条件下, 本文算法的消耗时间少, 搜索到的入围点数多, 入围率和平均重投影误差与其他算法接近, 消耗的内存空间与多探头局部敏感哈希算法相当。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. [本文引用:1]
[2]	聂海涛, 龙科慧, 马军, 等. 基于快速SIFT算法和模糊控制的人脸识别[J]. 吉林大学学报: 工学版, 2016, 46(2): 549-555. Nie Hai-tao, Long Ke-hui, Ma Jun, et al. Face recognition based on fast scale invariant feature algorithm and fuzzy control[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(2): 549-555. [本文引用:1]
[3]	Bay H, Ess A, Tuytelaars T, et al. Speeded-up robust features (surf)[J]. Computer Vision and Image Understand ing, 2008, 110(3): 346-359. [本文引用:1]
[4]	郭清达, 全燕鸣, 姜长城, 等. 应用摄像机位姿估计的点云初始配准[J]. 光学精密工程, 2017, 25(6): 1635-1651. Guo Qing-da, Quan Yan-ming, Jiang Chang-cheng, et al. Initial registration of point clouds using camera pos estimation[J]. Optics and Precision Engineering, 2017, 25(6): 1635-1651. [本文引用:1]
[5]	Calonder M, Lepetit V, Strecha C, et al. BRIEF: binary robust independent elementary features[J/OL]. [2017-03-22]. http: ∥icwww. epfl. ch/~lepetit/papers/calonder_eccv10pdf. [本文引用:2]
[6]	Rublee E, Rabaud V, Konolige K, et al. ORB: an efficient alternative to SIFT or SURF[J/OL]. [2017-03-25]. http: ∥www. cs. zju. edu. cn/~gpan/course/materials/ORB. pdf. [本文引用:1]
[7]	Leutenegger S, Chli M, Siegwart R Y. BRISK: binary robust invariant scalable keypoints[J/OL]. [2017-03-23]. http: ∥www. robots. ox. ac. uk/~vgg/rg/papers/brisk. pdf. [本文引用:1]
[8]	Alahi A, Ortiz R, Vand ergheynst P. FREAK: fast retina keypoint[J/OL]. [2017-03-24]. https: ∥infoscience. epfl. ch/record/175537/files/2069. pdf. [本文引用:1]
[9]	张展, 杨东升. 圆周二进制描述符的图像点特征提取方法[J]. 计算机辅助设计与图形学学报, 2017, 29(8): 1465-1476. Zhang Zhan, Yang Dong-sheng. Image point feature extraction algorithm of circumferential binary descriptor[J]. Journal of Computer-Aided Design & Computer Grphics, 2017, 29(8): 1465-1476. [本文引用:1]
[10]	Richard Szeliski. 计算机视觉-算法与应用[M]. 艾海舟, 兴军亮译. 北京: 清华大学出版社, 2012: 175-176. [本文引用:1]
[11]	Indyk P, Motwani R. Approximate nearest neighbor: towards removing the curse of dimensionality[J/OL]. [2017-03-23]. http: ∥www. cs. princeton. edu/courses/archive/spr04/cos598B/bib/IndykM-curse. pdf. [本文引用:2]
[12]	Lv Qin, Josephson William, Wang Zhe, et al. Multi-probe LSH: efficient indexing for high-dimensional similarity search[J/OL]. [2017-03-24]. http://www.cs.princeton.edu/cass/papers/mplsh_vldb07.pdf. [本文引用:1]
[13]	Kong Wei-hao, Li Wu-jun, Guo Min-yi. Manhattan hashing for large-scale image retrieval[C]∥Proceedings of the 35th International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 2012: 45-54. [本文引用:1]
[14]	Shrivastave Anshumali, Li Ping. Densifying one permutation hashing via rotation for fast near neighbor search[J/OL]. [2017-03-23]. http: ∥proceedings. mlr. press/v32/shrivastava14. pdf. [本文引用:1]
[15]	Lin Guo-sheng, Shen Chun-hua, Shi Qin-fen, et al. Fast supervised hashing with decision trees for high-dimensional data[C]∥IEEE Conference on Computer Vision& Pattern Recognition, Columbus, OH, USA, 2014: 1971-1978. [本文引用:1]
[16]	Liong Venice Erin, Lu Ji-wen, Wang Gang, et al. Deep hashing for compact binary codes learning[J/OL]. [2017-03-23]. https: //www. cv-foundation. org/openaccess/content_cvpr_2015/papers/Liong_Deep_Hashing_for_2015_CVPR_paper. pdf. [本文引用:1]
[17]	Lin Kevin, Yang Huei-fang, Hsiao Jen-hao, et al. Deep learning of binary hash codes for fast image retrieval[J/OL]. [2017-03-22]. http: ∥www. iis. sinica. edu. tw/~kevinlin311. tw/cvprw15. pdf. [本文引用:1]
[18]	Norouzi M, Fleet D J. Minimal loss hashing for compact binary codes[C]∥Proceedings of the 28th International Conference on Machine Learning, Bellevue, Washington, USA, 2011: 353-360. [本文引用:1]
[19]	Norouzi M, Punjani A, Fleet D J. Fast search in hamming space with multi-index hashing[J/OL]. [2017-03-25]. https: ∥www. cs. toronto. edu/~norouzi/research/papers/multi_index_hashing. pdf. [本文引用:1]
[20]	Muja M, Lowe D G. Fast matching of binary features[C]∥2012 Ninth Conference on Computer and Robot Vision, Toronto, ON, Canada, 2012: 404-410. [本文引用:1]
[21]	Muja M, Lowe D G. Scalable nearest neighbor algorithms for high dimensional data[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014, 36(11): 2227-2240. [本文引用:1]
[22]	Garcia-Molina H, Ullman J D, Widom J. 数据库系统实现[M]. 杨冬青, 吴愈青, 包小源译. 2版. 北京: 机械工业出版社, 2010: 688-693. [本文引用:2]
[23]	Mikolajczyk K, Schmid C. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis &Machine Intelligence, 2005, 27(10): 1615-1630. [本文引用:3]
[24]	邹瑜, 梁斌, 王学谦, 等. 基于旋转投影二进制描述符的空间目标位姿估计[J]. 光学精密工程, 2017, 25(11): 2958-2967. Zou Yu, Liang Bin, Wang Xue-qian, et al. Spacetarget pose estimation based on binary rotational projection histogram[J]. Optics and Precision Engineering, 2017, 25(11): 2958-2967. [本文引用:1]
[25]	崔少辉, 谢征, 王刚, 等. 二进制鲁棒不变尺度特征匹配电子稳像[J]. 光学精密工程, 2015, 23(9): 2715-2723. Cui Shao-hui, Xie Zheng, Wang Gang, et al. Feature matching electronic image stabilization based on binary robust in variant scalable keypionts[J]. Optics and Precision Engineering, 2015, 23(9): 2715-2723. [本文引用:1]
[26]	罗家祥, 林畅赫, 王加朋, 等. 结合深度卷积网络与加速鲁棒特征配准的图像精准定位[J]. 光学精密工程, 2017, 25(2): 469-476. Luo Jia-xiang, Lin Chang-he, Wang Jia-peng, et al. Accurate image positioning combining deep convolution network with SURF registering[J]. Optics and Precision Engineering, 2017, 25(2): 469-476. [本文引用:1]
[27]	熊昌镇, 单艳梅, 郭芬红. 结合主体检测的图像检索方法[J]. 光学精密工程, 2017, 25(3): 792-798. Xiong Chang-zhen, Shan Yan-mei, Guo Fen-hong. Image retrieval method based on image principal part detection[J]. Optics and Precision Engineering, 2017, 25(3): 792-798. [本文引用:1]

2004

0.0

... 0 引言二进制特征是图像特征匹配和识别的先进技术,相对于SIFT^[1,2]和SURF^[3,4]特征,其具有有效计算、快速比较和紧密存储的优点 ...

2016

0.0

. 2016, 46(2):549-555

Face recognition based on fast scale invariant feature algorithm and fuzzy control

基于快速SIFT算法和模糊控制的人脸识别

Nie Hai-tao , Long Ke-hui , Ma Jun

聂海涛, 龙科慧, 马军

... 0 引言二进制特征是图像特征匹配和识别的先进技术,相对于SIFT^[1,2]和SURF^[3,4]特征,其具有有效计算、快速比较和紧密存储的优点 ...

2008

0.0

... 0 引言二进制特征是图像特征匹配和识别的先进技术,相对于SIFT^[1,2]和SURF^[3,4]特征,其具有有效计算、快速比较和紧密存储的优点 ...

2017

0.0

. 2017, 25(6):1635-1651 DOI:doi:10.3788/OPE.20172506.1635

Initial registration of point clouds using camera pos estimation

应用摄像机位姿估计的点云初始配准

Guo Qing-da , Quan Yan-ming , Jiang Chang-cheng

郭清达, 全燕鸣, 姜长城

摘　要：基于摄像机位姿估计的数学模型,提出了一种检测摄像机位移前后目标图像特征点的方法,通过求解摄像机发生位移前后的相对位姿矩阵来解决应用视觉图像获得点云的初始配准问题。首先,介绍了摄像机位姿估计模型,包括本质矩阵、旋转矩阵以及平移矩阵;然后,介绍了SURF算子的特征点检测、描述和匹配的方法,在此基础上面向双目视觉和单目结构光系统,分别提出了摄像机位移前后目标图像SURF特征点匹配和深度估计模型;最后,分别进行双目视觉和单目结构光系统点云的获取、位移前后目标图像特征点检测匹配和深度估计实验,应用摄像机位姿估计模型求解旋转矩阵和位移矩阵,并对位移矩阵进行统计分析剔除粗差。实验中采用基于点云空间特征点和基于图像的方法进行对比,点云对应特征点均方误差缩小至12.46mm。实验结果验证了方法的可行性,表明本文的点云初始配准方法能较好地获得点云精确配准初值。

... 0 引言二进制特征是图像特征匹配和识别的先进技术,相对于SIFT^[1,2]和SURF^[3,4]特征,其具有有效计算、快速比较和紧密存储的优点 ...

0.0

... 目前,主要二进制特征的提取算法有BRIEF^[5]、ORB^[6]、BRISK^[7]、FREAK^[8]和CBD^[9]等 ...

... 1 二进制特征二进制特征的提取^[5,24,25]是根据特征点邻域中,对应的#cod#x0201c ...

0.0

... 目前,主要二进制特征的提取算法有BRIEF^[5]、ORB^[6]、BRISK^[7]、FREAK^[8]和CBD^[9]等 ...

0.0

... 目前,主要二进制特征的提取算法有BRIEF^[5]、ORB^[6]、BRISK^[7]、FREAK^[8]和CBD^[9]等 ...

0.0

... 目前,主要二进制特征的提取算法有BRIEF^[5]、ORB^[6]、BRISK^[7]、FREAK^[8]和CBD^[9]等 ...

2017

0.0

. 2017, 29(8):1465-1476

Image point feature extraction algorithm of circumferential binary descriptor

圆周二进制描述符的图像点特征提取方法

Zhang Zhan , Yang Dong-sheng

张展, 杨东升

... 目前,主要二进制特征的提取算法有BRIEF^[5]、ORB^[6]、BRISK^[7]、FREAK^[8]和CBD^[9]等 ...

2012

0.0

... 二进制特征即01字符串,一般使用汉明距离和最近邻比率算法^[10](NNDR)判断两个二进制特征是否匹配 ...

0.0

... 例如:Indyk等^[11]提出基于哈希表的近似近邻搜索算法#cod#x02014 ...

... 2 局部敏感哈希最初的局部敏感哈希算法^[11],需要将欧氏空间中的特征向量转换到汉明空间中,同时确定特征向量在哈希表中的位置,而二进制特征一般是由BRIEF、ORB等算法直接提取^[26,27] ...

2017

0.0

... Lv等^[12]提出多探头局部敏感哈希(MPLSH),有效地解决了高维特征的相似度搜索问题,且可用于匹配二进制特征搜索 ...

2012

0.0

... Kong等^[13]提出将曼哈顿哈希表用于大规模图像检索,把二进制特征转化为十进制数,根据曼哈顿距离计算不相似度进行查询 ...

0.0

... Shrivastave等^[14]通过旋转致密化位排列哈希,实现了高维二进制特征的快速近邻搜索 ...

2014

0.0

... Lin等^[15]提出在高维数据中使用决策树快速监督哈希算法 ...

0.0

... Liong等^[16]提出了基于紧凑二进制代码学习的深度哈希算法 ...

0.0

... Lin等^[17]提出了二进制哈希编码的深度学习算法,实现了图像的快速检索 ...

2011

0.0

... Norouzi等^[18]在紧凑二进制代码中,给出最小亏损哈希算法 ...

0.0

... 之后,采用多索引实现了在汉明空间的二进制代码子字符串的快速搜索,使在汉明空间的k近邻(KNN)搜索成为可能^[19] ...

2012

0.0

... Muja等^[20]在使用自动算法配置的快速近邻搜索中,给出多个随机KD树算法搜索高维匹配特征,在二进制特征快速匹配算法中提出了多层次聚类树(HCT)算法,在高维数据可扩展近邻算法^[21]中,对近似最近邻算法做出总结,并给出相应的近似近邻快速搜索的函数库(FLANN) ...

2014

0.0

2010

0.0

... 文献[22]提出了位图索引的近邻搜索算法,具有占用空间少和搜索速度快的优点 ...

... 3 位图索引位图索引 V是一个长度为 N的聚集位向量^[22], 每位的状态只能是0或1 ...

2005

0.0

... 本文实验使用文献[23]给出的图像数据集提取的ORB二进制特征,使用入围点数、入围率、平均查询时间、平均投影误差和空间复杂度等评价标准,将本文算法与FLANN函数库中的二进制特征匹配算法(包括LINEAR、MPLSH和HCT等)进行对比 ...

... 使用文献[23]给出图像数据集所提取的ORB二进制特征作为算法评价数据集 ...

... 文献[23]给出的图像数据集中,每个图库有6幅图像,且每个图库里的图像都是同一场景在不同情况下拍摄的 ...

2017

0.0

. 2017, 25(11):2958-2967

Spacetarget pose estimation based on binary rotational projection histogram

基于旋转投影二进制描述符的空间目标位姿估计

Zou Yu , Liang Bin , Wang Xue-qian

邹瑜, 梁斌, 王学谦

To estimate quickly the relative pose of a space target based on point cloud, a Binary Rotational Projection Histogram (BRoPH) feature descriptor was proposed. Firstly, a Local Reference Frame (LRF) for the feature point was established; Then, the density and depth images were generated under different views by rotationally projecting the local surface of feature point, Finally, the multi-scale binary string of the feature point was produced based on the images. For implementing the pose estimation of space target in real time, a Hamming distance threshold based feature matching strategy was proposed further to exclude false matching pairs to accelerate coarse pose estimation procedure. The comparison experiments were performed with SHOT descriptor and FPFH descriptor. The results demonstrate that BRoPH achieves an accurate pose estimation with only about 1/80 average memory cost of SHOT and FPFH descriptors. The average attitude error of BRoPH is under 0.1掳, and its average translation error is less than 1/180R. Besides, the Hamming distance threshold based feature matching strategy speeds up the subsequent RANSAC by 7 times, and the overall pose estimation frequency exceeds 7 Hz, which is 3 to 6.8 times faster than those of SHOT and FPFH descriptors respectively. The proposed feature descriptor is compact and efficient, and the pose estimation method is accurate and robust for the requirements of space target pose estimation.

... 1 二进制特征二进制特征的提取^[5,24,25]是根据特征点邻域中,对应的#cod#x0201c ...

2015

0.0

. 2015, 23(9):2715-2723

Feature matching electronic image stabilization based on binary robust in variant scalable keypionts

二进制鲁棒不变尺度特征匹配电子稳像

Cui Shao-hui , Xie Zheng , Wang Gang

崔少辉, 谢征, 王刚

... 1 二进制特征二进制特征的提取^[5,24,25]是根据特征点邻域中,对应的#cod#x0201c ...

2017

0.0

. 2017, 25(2):469-476 DOI:doi:10.3788/OPE.20172402.0469

Accurate image positioning combining deep convolution network with SURF registering

结合深度卷积网络与加速鲁棒特征配准的图像精准定位

Luo Jia-xiang , Lin Chang-he , Wang Jia-peng

罗家祥, 林畅赫, 王加朋

针对在大图像中定位小块区域图像的需求,本文提出一种结合深度卷积网络与加速鲁棒特征(SURF)配准的精准定位方法。将标准大区域图像分割成若干个小参考图像,利用深度卷积网络和类局部敏感哈希降维法提取参考图像集的特征并形成特征库;基于特征库,提出了先检索多个相似参考图像后再进行SURF精确配准的两阶段方法,实现目标小图像在标准大图像中的定位。针对电子工业过程中高密度柔性电路板(FPC)及精确末制导中的图像定位数据进行实验,实验结果表明,该方法避免了传统SURF算法大量的特征提取与配对过程,SURF特征提取数减少近90%;与直接根据图像特征进行配准的传统定位方法相比,在保证定位准确率的基础上,耗时可缩小一个数量级以上。

2017

0.0

. 2017, 25(3):792-798

Image retrieval method based on image principal part detection

结合主体检测的图像检索方法

Xiong Chang-zhen , Shan Yan-mei , Guo Fen-hong

熊昌镇, 单艳梅, 郭芬红