基于谱聚类矩阵的改进DNALA算法

引用本文

邓剑勋, 熊忠阳, 邓欣. 基于谱聚类矩阵的改进DNALA算法[J].吉林大学学报（工学版）, 2018,48(3): 903-908
DENG Jian-xun, XIONG Zhong-yang, DENG Xin. Improved DNALA algorithm based on spectral clustering matrix[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 903-908 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170114
Permissions

基于谱聚类矩阵的改进DNALA算法

邓剑勋^1,², 熊忠阳¹, 邓欣³

1.重庆大学计算机学院,重庆 400044

2.重庆电子工程职业学院软件学院,重庆 401331

3.重庆邮电大学计算机学院,重庆 400065

作者简介:邓剑勋(1978-),男,副教授,博士.研究方向:模式识别,图像处理.E-mail:dengjianxun@189.cn

基金:重庆市教委2015年度科学技术研究项目(kj1503004); 国家自然科学基金项目(61403054).

摘要

针对传统DNALA算法运行效率低、最终数据挖掘结果精度不理想等问题,提出了一种基于谱聚类矩阵的改进DNALA(DNALA-I)算法,提高了时间效率以及结果精度。该算法通过频谱聚类方法中的计算距离矩阵方法对传统DNALA算法中通过多序列比计算距离矩阵的方法进行改进,在不降低数据挖掘精度的前提下能够有效减少对齐序列所花费的时间,提高算法的运行效率。仿真实验结果表明:本文算法相较传统的DNALA算法不仅提高了时间效率,并且保证了实验结果的计算精度。

关键词: 计算机应用; 隐私保护; 数据挖掘; DNALA算法; 频谱聚类矩阵

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2018)03-0903-06

Improved DNALA algorithm based on spectral clustering matrix

DENG Jian-xun^1,², XIONG Zhong-yang¹, DENG Xin³

1.College of Computer Science,Chongqing University,Chongqing 400044,China

2.School of Software,Chongqing College of Electronic Engineering,Chongqing 401331,China

3.School of Computer Science and Technology, Chongqing University of Posts and Telecommunications,Chongqing 400065,China

Abstract

Traditional DNALA algorithm has the shortcomings of low efficiency in terms of running time and unsatisfactory accuracy of the data mining results. To overcome these shortcomings, an improved DNALA algorithm is proposed based spectral clustering matrix, called DNALA-I, which can improve the time efficiency and accuracy of the results. The calculation of the distance matrix by multi sequence ratios in the traditional DNALA algorithm is improved by calculation of the spectral clustering distance matrix in the DNALA-I algorithm. Experiment results show that, compared with the traditional DNALA algorithm, the proposed DNALA-I algorithm can effectively reduce the time for sequence alignment meanwhile remain the data mining accuracy.

Keyword: computer application; privacy protection; data mining; DNALA algorithm; spectrum clustering matrix

文章图片

0 引言

数据库技术的飞速发展导致数据量呈指数级增长^[1]。面对巨量的数据, 单靠人工进行统计分析显然不现实, 这就促进了数据挖掘技术的快速发展^[2]。目前, 数据挖掘技术不断由低精度、低深度向高精度、高深度发展, 当人们利用数据挖掘技术对巨量数据进行分析和挖掘时, 不得不面对这些数据的隐私保护问题^{[3, 4, 5]}。

在数据挖掘领域已经有许多专家学者提出了防止用户个人隐私数据泄露的数据挖掘算法, 其中事务型数据隐私保护问题是一个重要的研究方向。Terrovitis等^[6]将关系型数据k-匿名化处理算法应用到事务型数据中, 提出了k^m-匿名化算法。该算法的前提是集合里项目的数目不能大于m, 并且该集合必须被数目不低于k的事务记录所包含。该算法的缺点是:当巨量数据中含有一定量的非正常数据项目时, 数据容易被概化过度, 进而导致数据信息损失过多, 影响最后的信息精度。k^m-匿名化采用的是全局概化技术^[7], 后来一些专家学者对该算法进行了改进, 提出了采用局部概化技术的事务型匿名原则, 该原则要求更为苛刻, 但缺点就是破坏了原始数据的域互斥性^[8]。Xu等^[9]提出了一种新的采用全消隐技术的 $(h, k, p) -$ 内聚原则, 该算法的核心是一个集合中公开项目的数目不能低于 $p$ 个, 并且该集合要出现在数目不少于 $k$ 的事务记录中, 同时这些事务记录中必须保证数目不高于 $h \times k$ 个事务记录包括同一个私密项目。 $k^{m} -$ 匿名化实际上是 $(h, k, p) -$ 内聚原则的一个特例。 $(h, k, p) -$ 内聚原则的缺点是:当原始数据过于稀疏时, 采用该原则会导致数据信息损失过大。后来又有学者提出带宽矩阵方法, 基本思想是将事务记录进行排列分组, 在各个组里面将私密项目进行随机排序处理, 以便达到事务多元化, 其缺点是最后得到的数据挖掘结果不太合理^[10]。

以上几种数据挖掘隐私保护技算法都较为经典, 并且还有很多其他基于聚类算法的隐私保护技术^[11]。本文提出了一种基于谱聚类矩阵的改进DNALA(DNALA-improved, DNALA-I)算法, 对传统DNALA算法中距离矩阵的计算方法进行了改进, 提高了时间效率以及结果精度。

1 本文算法

1.1 DNALA算法

DNALA算法通常用来保护个人DNA数据隐私安全, 属于经典的数据挖掘中个人数据隐私保护算法, 原理是在个人的DNA数据维护中融入k-匿名(k-Anonymitya)方法, 从而得到DNALA算法。它的主要攻击方式是路径攻击, 该算法主要是采用模糊化方式处理DNA数据, 进而确保数据库的序列存在与其相一致的序列(这一序列表示为k-1个, 但是在实践中, 一般选择k=2), 这样可以有效杜绝路径的干扰。但是, 该方法保证数据安全的代价是牺牲了数据的准确性^[12]。

DNALA算法步骤为:①将数据库的数据逐一展开并进行多序列对比, 运用的算法和工具有多种, 在文献[2]中的计算方法为CLUSTALW; ②距离矩阵由对比结果和DNA单字符表示法的兼容性两部分构成。

DNALA算法能够有效保护DNA数据中的个人隐私, 但也存在明显缺陷^[13]。DNALA算法中通过多序列对比来计算距离矩阵, 这种机制属于纯动态规划, 缺点是复杂度极高、计算效率较低。从而导致在DNA数据预处理阶段, 算法时间成本太高, 必须借助别的算法进行额外加速。并且DNALA算法数据预处理阶段采用贪心算法对序列进行分组, 分组效果不是特别理想^[14]。

本文算法将传统数据挖掘算法中的数据对象转换为空间数据对象, 利用频谱聚类方法中的计算距离矩阵方法对传统DNALA算法中通过多序列对比计算距离矩阵的方法进行改进。在传统聚类算法的基础上, 通过谱图机制分析出聚类结果, 实现了距离矩阵算法与谱聚类算法的有机结合, 大大降低了数据预处理阶段序列分组的复杂度, 节省了时间, 提高了算法效率。同时, 该算法采用双序列对比, 相较DNALA算法能够进一步减少序列排列所花费的时间, 并且增加了序列对比的灵活性。

1.2 DNALA-DMA矩阵的谱聚类矩阵

谱聚类算法用于处理图像空间最优划分数据, 其机制是将数据向数据点转变之后连接这些数据点, 从而组合成图^[15]。DNA序列算法将根据前文介绍的谱聚类算法的特点, 结合DNA序列可以被认为是储存于空间的图像数据这一特征来完善DNALA算法, 有利于提升算法效率, 也有利于完善算法的精准度。本文采用其非对称规范Laplace矩阵的方法计算距离矩阵。

1.2.1 聚类

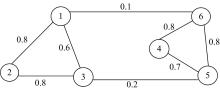
谱聚类算法是一种基于图论的聚类方法。在谱聚类算法内, 通常用高斯核函数计算相似矩阵 $S,$ 同时高斯核函数也是径向基函数(沿径向对称的标量函数)。 $G (V, E)$ 为无相加权图, $V = {X_{1}, X_{2}, \dots, X_{n}}$ 为点的集合, 每个实验数据一一对应集合中的点。两点之间所构成的权重集合 $E = {W_{12}, W_{23}, \dots, W_{ij}, W_{nn}},$ 该集合是指每个点间的关系, 每两个点之间的相似度主要是指每两个点连线间的权重值。

由图1可知, 该图能够视为2个部分构成, 可以将它们分别做聚类泛化处理得到最佳结果。但是由于在实际应用中并非全部数据都是正常数据, 常常会出现难于处理的异常数据, 这时候就会增加划分数据的复杂度。该情况下应当制定标准的数据划分方法, 以确保数据点能够得到有效的划分。

	Figure Option View Download New Window
	图1 无相加权图Fig.1 No phase weighted graph

定义(划分) 由于划分代表着各种类包含的2个点连线形成的边的集合。因此, 其公式为:

$cut (A, B) = \sum_{i \in A, j \in B} W_{ij} (1)$

将以上标准问题归类为获得最小划分问题。结合图1可知其划分所采取的公式为:

$cut (A, B) = W_{16} + W_{35} = 0.3 (2)$

全面考虑各类的相互关系, 并对其内部的密度性加以权衡, 以便兼顾类的内、外部状态, 那么可得获取最佳划分的评价标准公式为:

$minNcut (A, B) = \frac{cut (A, B)}{vol (A)} + \frac{cut (A, B)}{vol (B)} (3)$

式中:Ncut(· )表示最佳划分; $vol (A) 、 vol (B)$ 分别为类 $A 、 B$ 相应点的权重之和, 各种类的相互的关系是借助该权重之和进行有效规范。

采用该评价标准有利于获取最佳划分, 其优势为充分借助各种类包含的内、外部关系, 以确保状态得到最优平衡。

1.2.2 基于谱聚类的规范Laplace矩阵

选取 $V_{i}$ 代表样本的顶点, 其度的计算公式为:

$d_{i} ≜ \overset{n}{\sum_{j = 1}} W (i, j) (4)$

顶点集的度矩阵为:

$D ≜ diag (d_{1}, d_{2}, \dots, d_{n}) (5)$

谱聚类算法一般采用的矩阵如下所示。

$n \times n$ 矩阵的相似矩阵为:

$S ≜ W (6)$

Laplace矩阵为:

$L ≜ D - S (7)$

转移概率矩阵为:

$S_{rw} ≜ D^{- 1} S (8)$

非对称规范Laplace矩阵为:

$L_{rw} ≜ D^{- 1} (D - S) (9)$

规范相似矩阵为:

$S_{sym} ≜ D^{- 1 / 2} S D^{- 1 / 2} (10)$

对称规范Laplace矩阵为:

$L_{sym} ≜ D^{- 1 / 2} (D - S) D^{- 1 / 2} (11)$

在转移概率矩阵 $S_{rw}$ 中, 按照从大到小的顺序对特征值进行排列, 构建 $S_{rw}$ 的前 $K$ 项特征向量组; 在规范Laplace矩阵中, 按照从小到大的顺序对特征值进行排列, 构建规范Laplace矩阵的前 $K$ 项特征向量组。

在谱聚类算法中, 采用高斯核函数对距离矩阵进行转换来计算相似矩阵。一般而言, 相似矩阵 $S$ 是借助全局高斯核函数来实现对距离矩阵的转换, 其公式为:

$S_{ij} = \exp (- \frac{d_{ij}^{2}}{σ^{2}}) (12)$

式中: $σ$ 为全局高斯核函数参数; $d_{ij}$ 为数据点的距离, 也就是 $i$ 与 $j$ 两者间的距离, 其计算公式为:

$d_{ij} ≜ \overset{n}{\sum_{j = 1}} W (i, j) (13)$

1.3 DNALA-I距离矩阵算法

多路归一化割普聚类方法属于普聚类算法之一, 它的性能优良, 且其普聚类矩阵属于非对称规范Laplace矩阵。因此, 本文围绕扰动理论, 在DNALA算法中积极融合非对称规范Laplace矩阵的优势, 改进其计算距离矩阵的方法, 一方面加强了算法的运行效率; 另一方面提升了信息的安全性, 全面保护个人隐私。

1.3.1 DNALA-I序列对比

序列对比通常是用于汇总、分析各类数据, 并且结合各类方法来寻求规律性, 在模式识别、机器学习以及数据挖掘等领域应用广泛。

双序列对比通常是以DNA序列为基础, 对其相应的元素逐一加以对比, 确保对比结果的正确性和准确性, 保障个人信息安全。因此, 需要事先围绕原始序列做出相应处理, 其具体步骤如下:

(1)插入(Insertion):将字符插入到DNA序列中, 如将几个空格分别插入到序列中, 用“ -” 表示。

(2)删除(Deletion):选择序列里面的字符, 对其进行删除操作, 如选中序列里面包含的空格, 对其进行删除, 用“ -” 表示。

(3)替换(Substitution):选中序列, 将需要的字符进行替换操作。

选取序列 $S$ 和 $T, S = (s [1], s [2], \dots, s [m]) 、 T = (t [1], t [2], \dots, t [n])$ , 然后对得分情况进行最优对比, 确认初值以后, 通过递归公式计算 $M (i, j)$ 值, 即:

$\begin{array}{l} M_{i, j} = \max \{\begin{array}{l} M_{i - 1, j} + σ (s [i], -) \\ M_{i - 1, j - 1} + σ (s [i], t [j]) \\ M_{i, j - 1} + σ (-, t [j]) \end{array} (14) \\ 式中 : \\ M_{i, o} = \overset{i}{\sum_{k = 0}} σ (s [i], -) (15) \\ M_{i, o} = \overset{i}{\sum_{k = 0}} σ (-, T [j]) (16) \end{array}$

选取 $S 、 T$ 两条DNA序列, 已知相似矩阵时, 采用回溯法计算最优对比, 其详细步骤如下所示。

(1)对序列 $S 、 T$ 的两个相似矩阵进行初始化。

(2)两个碱基的得分需要根据得分递推公式和替换矩阵进行详细填写。

(3)以得分矩阵为基础, 从矩阵对应的右下方位开始, 由最大分值依次做路线回溯操作。

(4)将回溯路线转化成对比结果, 也就是完成插入空格等相关操作。

这一序列对比的对象是偶数序列, 但是在实际过程中并非只有偶数序列, 也常出现奇数序列。假如原始序列集合的序列全部属于奇数, 则最终一个序列对比包含3条序列, 但是本部分仅是针对双序列为对比对象来进行距离矩阵的计算, 所以, 在多序列对比时, 只要再增加一次对这3个序列的对比即可。由于数量不多, 可以快速获得其对比结果。

1.3.2 DNALA-I距离矩阵计算

就DNALA序列而言, 如果两个字符被泛化, 需要通过距离衡量信息受到的损失。本文基于规范Laplace矩阵全面改进DNALA序列矩阵。字符 $a$ 和 $b$ 在经过泛化后其结果以 $g (a, b)$ 表示, 那么, $S$ 与 $T$ 序列长度相同, 并且经过泛化后, 可以将其结果定义成根据 $g (S [1], T [1], g (S [2], T [2], \dots, g (S [n], T [n])$ 构建的序列组合。并且, $n$ 表示序列 $S$ 和 $T$ 两者的总长, $S [i]$ 为序列 $S$ 的第 $i$ 字符, $T [i]$ 为序列 $T$ 的第 $i$ 字符, 也可以理解为 $g {(S, T)}_{[i]} = g (S [i], T [i]) 。$

用 $x 和 y$ 表示两个字符, 则两者间的距离为:

$dis (x, y) = 2 \times lev (g (x, y)) - lev (x) - lev (y) (17)$

式中:lev(· )为字符“ · ” 所在的层。

序列 $S$ 与 $T$ 的长度相同, 将两个序列间的距离定义为两个序列各自的字符距离之和, 其计算公式为:

$dis (S, T) = \overset{n}{\sum_{t = 1}} dis (S [i], T [j]) (18)$

以Laplace矩阵所具备的特点以及扰动原理为中心, 计算DNA序列泛化后距离的新算法详细步骤如下所示。

(1)选取一个矩阵 $R$ , 通过以下步骤将R转化为相似矩阵 $R' :$

Step1 $d_{i, j}$ 为原始矩阵的距离, 将其转变为新的相似距离 $d'_{i, j}$ , 其公式为:

$\begin{array}{l} d'_{i, j} = \\ \{\begin{array}{l} i = j \\ 1 - 10^{- 4} \overset{n}{\sum_{k = i, k \neq j}} [\frac{2 (d_{ik} \land d_{jk})}{d_{ik} + d_{jk}} \log (\frac{2 (d_{ik} \lor d_{jk})}{d_{ik} + d_{jk}}) + \\ \frac{2 (d_{ik} \lor d_{jk})}{d_{ik} + d_{jk}} \log (\frac{2 (d_{ik} \land d_{jk})}{d_{ik} + d_{jk}})], i \neq j \end{array} (19) \end{array}$

式中: $i 、 j 、 k$ 为各种物种, $d_{ik} \land d_{jk} = \min {d_{ik}, d_{jk}}, d_{ik} \lor d_{j k} = \max {d_{ik}, d_{jk}} 。$

Step2 相似矩阵 $R'$ 的转变需要通过以下公式:

$r_{ij} = \frac{\overset{n}{\sum_{t = 1}} \min {d'_{it}, d'_{jt},}}{0.5 \overset{n}{\sum_{t = 1}} [d'_{it}, d'_{jt}]} (20)$

式中: $r_{ij}$ 为相似距离。

(2)选取 $R'$ 代表相似距离矩阵, 通过传递闭包法可以得到 $\bar{R},$ 也就是通过两两合成, 借助平方法来得到 $\bar{R},$ 那么 $\bar{R}$ 可以视为模糊等价矩阵。

(3)将 $\bar{R}$ 中挑选的值依次加以排序, 可以获得分区序列为: $π_{a 1}, π_{a 2}, \dots, π_{ak},$ 然后对物种做出聚类处理。

(4)当分区序列值全部选取完毕后, 就可以得出一棵进化树。

DNALA-I算法侧重于聚成含有两条序列的类, 如果前置条件是出现奇数条序列, 一个类就会含有3条序列, 每条记录需要得到有效的区分。

2 算法验证

本文的实验数据来自文献[16]中的数据I和数据II, 通过Matlab软件实现仿真验证。本文首先将DNA序列中含有的数据流信息放入度量空间; 然后通过弱聚类的数据流匿名化框架实现数据匿名化, 以便维护用户隐私, 其原理是将处于DNA数据集里面的数据流信息视为空间点; 最后对其进行距离矩阵和相似度计算。DNA序列数据经过匿名化处理后, 不会严重影响原始DNA序列的数据信息。

2.1 序列对齐所需时间对比

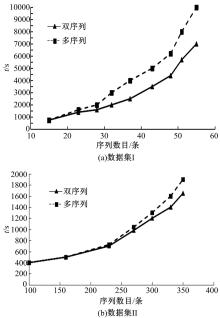
通过双序列以及多序列的对比方法, 将两个数据集中所含有的子序列进行对比, 同时将对齐序列所耗费的时间进行计算, 结果如图2所示。由图2可见, 与多序列对比而言, 双序列对比更加节约时间, 数据集I对该现象的呈现十分显著。

	Figure Option View Download New Window
	图2 不同序列对齐方法所需时间的对比Fig.2 Comparisons of time required for different sequential alignment methods

2.2 原始序列与其泛化序列间的距离计算结果对比

采用不同算法计算原始序列与其泛化序列间的平均距离, 结果如表1和图3所示。即使在同一实验环境中, 得到的值也会有偏差, 因此, 对一个数据进行多次实验, 取3次实验的平均值。

表1 使用不同方法计算序列与其泛化结果间的平均距离 Table 1 Mean distance between sequence and its generalization results using different methods

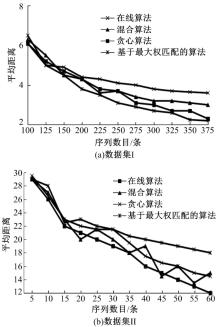	Figure Option View Download New Window
	图3 原始序列与其泛化序列间的平均距离对比Fig.3 Average distance between original sequence and its generalization sequence

通过多序列、双序列两种方法进行序列对比, 然后计算其距离矩阵。同时对其进行聚类, 并对聚类结果做泛化处理, 取两者的平均距离。由表1可以看出:在确保聚类算法精度的前提下, 若想减少计算距离矩阵平均距离的时间, 可以借助多序列、双序列这两种对比方法来有效对齐序列, 这样还能够进一步提升计算结果的精度。

从上述实验结果可以看出:将DNALA-I距离矩阵计算方法运用到DNA序列集合中, 能够大大提升序列对比的时间效率, 同时也提升了聚类算法的精度。

3 结束语

提出了基于谱聚类矩阵的改进的DNALA算法— — DNALA-I(DNALA-improved)算法。该算法通过频谱聚类方法中的计算距离矩阵方法对传统DNALA算法中通过多序列比来计算距离矩阵的方法进行改进, 在不降低数据挖掘精度的情况下, 本文算法能够有效减小对齐序列所花费的时间, 提高时间效率。仿真实验结果表明:本文算法相较传统的DNALA算法不仅提高了时间效率, 并且保证了实验结果的计算精度。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Miao G X, Tatemura J, Hsiung W P, et al. Extracting data records from the web using tag path clustering[C]∥Proceedings of the 18th International Conference on World Wide Web, Madrid, Spain, 2009: 981-990. [本文引用:1]
[2]	Zhou K, Snyder J M, Guo B N, et al. Stretch-driven mesh parameterization using spectral analysis[J/OL]. [2017-02-10]. https: ∥www. microsoft. com/en-us/research/wp-content/uploads/2017/01/isochart. pdf. [本文引用:2]
[3]	Atherton P J, Szewczyk N J, Selby A, et al. Cyclic stretch reduces myofibrillar protein synthesis despite increases in FAK and anabolic signalling in L6 cells[J]. The Physiological Society, 2009, 587(14): 3719-3727. [本文引用:1]
[4]	Siahpirani A F, Ay F, Roy S. A multi-task graph-clustering approach for chromosome conformation capture data sets identifies conserved modules of chromosomal interactions[J]. Genome Biology, 2016, 17(1): 114. [本文引用:1]
[5]	Sousa C, Grosso F, Meirinhos-Soares L, et al. Identification of carbapenem-resistant Acinetobacterbaumannii clones using infrared spectroscopy[J]. Journal of Biophotonics, 2014, 7(5): 287-294. [本文引用:1]
[6]	Terrovitis M, Bakiras S, Papadias D, et al. Constrained shortest path computation[C]∥International Conference on Advances in Spatial and Temporal Databases, Angra dos Reis, Brazil, 2005: 181-199. [本文引用:1]
[7]	Wechsler H. Intelligent biometric information management[J]. Intelligent Information Management, 2010, 2(9): 499-511. [本文引用:1]
[8]	Bettebghor D, Leroy F H. Overlapping radial basis function interpolants for spectrally accurate approximation of functions of eigenvalues with application to buckling of composite plates[J]. Computers & Mathematics with Applications, 2014, 67(10): 1816-1836. [本文引用:1]
[9]	Xu D, Xu D, Luo J. A free-roaming mobile agent security protocol based on anonymous onion routing and k anonymous hops backwards[C]∥International Conference on Autonomic and Trusted Computing. Berlin: Springer-Verlag, 2008: 588-602. [本文引用:1]
[10]	Bronstein A M, Bronstein M M, Guibas L J, et al. Shape Google: geometric words and expressions for invariant shape retrieval[J]. ACM Transactions on Graphics, 2009, 28(4): 106. [本文引用:1]
[11]	Liu Zhen-qiu, Guo Zhong-min, Tan Ming. Constructing tumor progression pathways and biomarker discovery with fuzzy kernel kmeans and DNA methylation data[J]. Cancer Informatics, 2008(6): 1-7. [本文引用:1]
[12]	Vega-Pons S, Ruiz-Shulcloper J. A survey of clustering ensemble algorithms[J]. International Journal of Pattern Recognition & Artificial Intelligence, 2011, 25(3): 337-372. [本文引用:1]
[13]	Perry S W, Norman J P, Barbieri J, et al. Mitochondrial membrane potential probes and the proton gradient: a practical usage guide[J]. Biotechniques, 2011, 50(2): 98-115. [本文引用:1]
[14]	Schwarzbach A E, Mcdade L A. Phylogenetic relationships of the mangrove family Avicenniaceae based on chloroplast and nuclear ribosomal DNA sequences[J]. Systematic Botany, 2002, 27(1): 84-98. [本文引用:1]
[15]	Mutwil M, Klie S, Tohge T, et al. PlaNet: combined sequence and expression comparisons across plant networks derived from seven species[J]. Plant Cell, 2011, 23(3): 895-910. [本文引用:1]
[16]	Kannangara R, Branigan C, Liu Y, et al. The transcription factor WIN1/SHN1 regulates cutin biosynthesis in arabidopsisthaliana[J]. Plant Cell, 2007, 19(4): 1278-1294. [本文引用:1]

2009

0.0

... 0 引言数据库技术的飞速发展导致数据量呈指数级增长^[1] ...

0.0

... 面对巨量的数据,单靠人工进行统计分析显然不现实,这就促进了数据挖掘技术的快速发展^[2] ...

... DNALA算法步骤为:①将数据库的数据逐一展开并进行多序列对比,运用的算法和工具有多种,在文献[2]中的计算方法为CLUSTALW ...

2009

0.0

... 目前,数据挖掘技术不断由低精度、低深度向高精度、高深度发展,当人们利用数据挖掘技术对巨量数据进行分析和挖掘时,不得不面对这些数据的隐私保护问题^[3,4,5] ...

2016

0.0

2014

0.0

2005

0.0

... Terrovitis等^[6]将关系型数据k-匿名化处理算法应用到事务型数据中,提出了k^m-匿名化算法 ...

2010

0.0

... k^m-匿名化采用的是全局概化技术^[7],后来一些专家学者对该算法进行了改进,提出了采用局部概化技术的事务型匿名原则,该原则要求更为苛刻,但缺点就是破坏了原始数据的域互斥性^[8] ...

2014

0.0

2008

0.0

... Xu等^[9]提出了一种新的采用全消隐技术的 h,k,p-内聚原则,该算法的核心是一个集合中公开项目的数目不能低于 p个,并且该集合要出现在数目不少于 k的事务记录中,同时这些事务记录中必须保证数目不高于 h×k个事务记录包括同一个私密项目 ...

2009

0.0

... 后来又有学者提出带宽矩阵方法,基本思想是将事务记录进行排列分组,在各个组里面将私密项目进行随机排序处理,以便达到事务多元化,其缺点是最后得到的数据挖掘结果不太合理^[10] ...

0.0

... 以上几种数据挖掘隐私保护技算法都较为经典,并且还有很多其他基于聚类算法的隐私保护技术^[11] ...

2011

0.0

... 但是,该方法保证数据安全的代价是牺牲了数据的准确性^[12] ...

2011

0.0

... DNALA算法能够有效保护DNA数据中的个人隐私,但也存在明显缺陷^[13] ...

2002

0.0

... 并且DNALA算法数据预处理阶段采用贪心算法对序列进行分组,分组效果不是特别理想^[14] ...

2011

0.0

... 2 DNALA-DMA矩阵的谱聚类矩阵谱聚类算法用于处理图像空间最优划分数据,其机制是将数据向数据点转变之后连接这些数据点,从而组合成图^[15] ...

2007

0.0

... 2 算法验证本文的实验数据来自文献[16]中的数据I和数据II,通过Matlab软件实现仿真验证 ...