作者简介:底晓强(1978-),男,副教授,博士生导师.研究方向:网络与信息安全.E-mail:dixiaoqiang@126.com
针对采用混沌视频加密算法后视频编码延迟大的问题,提出了一种H.264/AVC视频的快速安全加密算法。首先设计了密钥生成方案,由4维量子细胞神经网络迭代产生4组混沌序列,使用前3组混沌序列作为计算密钥的混沌序列池,后1组混沌序列作为Logistic混沌映射的初值以提高其初值的动态性。然后,利用Logistic混沌映射生成的索引从混沌序列池中选择用于生成密钥的序列组,避免了多次求解高维混沌系统,实现了密钥的快速生成。最后,本算法选择视频编码中的部分关键语法元素作为加密对象,减少了加密的数据量,对70帧的视频编码的延迟小于0.6%,通过密钥空间分析、NIST SP 800-22测试、已知明文攻击和推理攻击等实验分析表明,本文提出的视频加密算法具有密钥空间大、密钥随机性好、抗攻击性能强和安全强度高的优点。此外,算法不改变视频压缩比、符合视频编码格式规范,通过快速生成密钥和只加密视频关键语法元素有效地降低了H.264/AVC视频的加密延迟。
To solve the large delay problem of video coding by using the chaotic encryption, a fast security encryption algorithm for H.264/AVC video is proposed. First, a key generation scheme is designed. Four groups of chaotic sequences are generated with four-dimensional Quantum Cellular neural Network (QCNN) iteration, the first three groups are used for chaotic sequence pool, and the other one is used to generate the initial value of the Logistic map to increase the dynamics of the initial value. Then, to avoid repeatedly solving the high dimensional chaotic systems, the sequence of the calculation key is selected from the chaotic sequence pool according to the index generated by the Logistic map. After calculation, the encryption key is obtained, which realizes the fast generation of the key. Finally, some key elements, such as partial sign bits and information bits in video coding, are effectively encrypted for reducing the amount of encrypted data. Experiments show that the proposed encryption algorithm for 70 frames of video coding delay is less than 0.6%. Through the key space analysis, NIST SP 800-22 test, known plaintext attack and inference attack experiment analysis, it is shown that the proposed video encryption algorithm has the advantages of large key space, good random key, strong attack resistance and high security. In addition, the algorithm does not change the video compression ratio to conform video encoding format specification. By quickly generating secure keys with only encrypting the key video syntax elements, the H.264/AVC video encryption delay is effectively reduced.
视频加密是一种利用密码学的方法来保护视频信息安全的技术。H.264/AVC[1]由于其高效的压缩性能和良好的图像编码质量, 在网络视频传输中得到了广泛的应用。研究者们针对H.264/AVC提出了多种加密算法, 根据加密方式的不同, 可分为选择性加密算法和完全加密算法。完全加密算法是把视频数据作为二进制流直接加密, 但其计算复杂度高, 会改变视频格式, 导致标准解码器无法正常解码视频。选择性加密算法是对视频的关键数据加密, 具有加密数据量小、计算复杂度低等优点[2]。因此结合视频的编码格式, 对视频的关键数据加密的选择性加密算法得到了研究者的广泛关注。
视频选择性加密方法可分为帧内预测加密[3]、运动矢量残差(MVD)加密[4, 5]、离散余弦变换(DCT)的系数加密[6]和熵编码加密[7, 8, 9]。文献[2]发现帧内预测加密会改变视频的压缩比。MVD的数值加密有可能使运动矢量漂移, 导致无法正常解密视频[5]; MVD的符号位加密不会改变视频的压缩比且感知安全性较好, 但由于符号位只有2个数值, 因此无法抵抗明文攻击[9]。对于熵编码加密, Shahid等[7]提出了加密T1s和非零系数后缀的加密方法, 文献[8, 9]研究发现只加密非零系数的符号位能达到与加密非零系数后缀相似的加密效果, 而且由于减少了加密元素, 可降低加密算法的计算复杂度。
混沌系统可产生安全强度高的密钥, 对图像加密可取得良好的加密效果[10, 11], 但由于求解高维混沌系统运算时间长[12], 导致算法的编码延迟较大。本文使用量子细胞神经网络(Quantum cellular neural network, QCNN)生成4组混沌序列, 前3组作为混沌序列池, 最后1组作为Logistic混沌映射的初值以确保Logistic混沌映射初值的随机性。利用Logistic混沌映射生成2个索引值, 根据索引值从混沌序列池中选出2组混沌序列, 然后按位比较大小生成布尔密钥。重复这个过程直到获取足够的密钥, 使用这种方法避免了多次求解超混沌系统生成密钥, 同时基于上文的讨论, 本文提出的视频加密算法选择T1s的符号位、非零系数的符号位和运动矢量的符号位作为视频的加密对象, 减小了视频加密的数据量, 有效地降低了视频加密时的编码延迟。
本节将介绍加密视频数据所使用的混沌系统及混沌密钥生成方法。
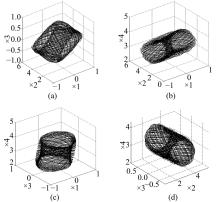
Lent等[13]利用量子点提出了量子点细胞自动机(Quantum-doc cellular automata, QCA), 量子计算的方法具有超高集成密度和低功耗的特点[14], 通过QCA可构造细胞局部耦合量子细胞神经网络QCNN[15]。由于量子点之间的量子相互作用, QCNN量子力学方程可从每个细胞的极化率获得复杂的动力学特性[16]。
对于由双细胞耦合的量子细胞神经网络, 其混沌系统状态方程为:
式中:
当
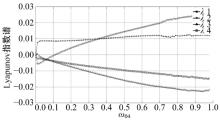
通过计算QCNN系统的 Lyapunov指数
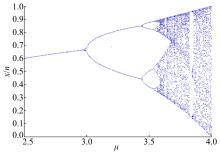
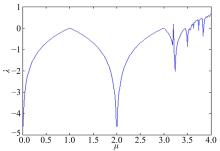
Logistic映射是一维离散混沌系统, 具有运算速度快的特点, 如式(2)所示:
式中:
Logistic的分岔过程和Lyapunov指数如图3和 4 所示, 当
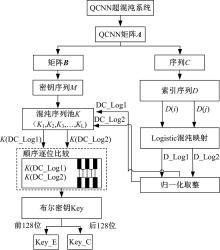
密钥生成的流程图见图5。将QCNN混沌系统方程(2)迭代
将QCNN矩阵
对矩阵
将
将序列
式中:
索引生成算法如下。
i=1; //i表示索引序列D的下标
m=1; //m表示当前编码的帧号
if(m==1)
#取D(i)迭代Logistic混沌映射N1次得到D_Log1
D_Log1=Logistic(D(i), N1, μ )
#D_Log1是一个[0, 1]之间的数, 将D_Log1映射到[1, n]之间
j=mapminmax(D_Log1, 1, n)
#取D(j)迭代Logistic混沌映射N2次得D_Log2
#N1, N2可以根据用户对安全强度的需求自行选择
D_Log2=Logistic(D(j), N2, μ )
# D_Log2为一个[0, 1]之间的数, 将D_Log2映射到[1, n]之间
i=mapminmax(D_Log2, 1, n)
m=m+1
else
#每编码一帧图像
While(m< =k)
#当m> 1时, 取D(i)迭代Logistic混沌映射次N1得D_Log1
D_Log1=Logistic(D(i), N1, μ )
j=mapminmax(D_Log1, 1, n)
if(j=i)
j=i+1
if(j> n)
j=1
D_Log2=Logistic(D(j), N2, μ )
i=mapminmax(D_Log2, 1, n)
#输出D(i)、D(j)
m++
按索引生成算法算法从D中取出D(i)和D(j)(i, j=1, 2, …, n)作为初值, 进行Logistic变换生成D_Log1、D_Log2, 把D_Log1、D_Log2映射到[1, L]区间, 再按式(6)向上取整得到[1, L]区间的整数DC_Log1、DC_Log2, 式(6)中的ceil()表示向上取整。
以DC_Log1和DC_Log2作为索引从混沌序列池
将密钥前128位Key_E加密视频的Exp-Golomb编码, 后128位Key_C加密视频的CAVLC编码。
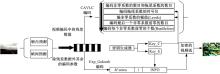
针对H.264/AVC主要档次的视频编码加密流程如图6所示, 视频帧内和帧间预测编码完成后, 使用CAVLC编码残差数据, 其余数据使用Exp-Golomb编码。将1.3节中生成的密钥Key_C 加密CAVLC编码的T1s的符号位和非零系数的符号位, Key_E加密Exp-Golomb编码的INFO。
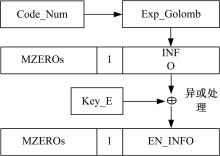
Exp-Golomb编码的标准结构是[M zeros] 1 [INFO], 它包括3部分, M zeros 表示M 位的0, 中间的“ 1” 是标志位, INFO是信息位, 信息位的长度等于M, 码字结构见表1。
| 表1 哥伦布码字结构 Table 1 Exp-Golomb code struct |
从表1可知, 输入数据Code_Num时, 根据下面两式:
可分别计算出比特串的信息位长度M和信息位INFO。式(8)中的floor()表示向下取整函数, 加密时使用
式中:INFO为原编码的信息位; Key_E为1.3节生成的密钥; En_INFO为加密的信息位, 其解密过程是加密的逆过程。
对INFO 加密, 其加密过程如图7所示。
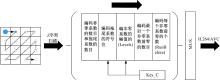
CAVLC编码过程如图8所示, Z字形扫描后的数据使用CAVLC编码, CAVLC编码过程包含:①对非零系数的个数(TotalCoeffs)和拖尾系数的个数(TrailingOnes)编码; ②对每个拖尾系数的符号编码; ③对除了拖尾系数以外的非零系数幅值(Levels)编码; ④对最后一个非零系数前零的个数(TotalZeros)编码; ⑤对每一个非零系数前零的个数(RunBefore)编码。拖尾系数的符号位和剩余非零系数的符号位在编码过程中用于保持位流的规范性, 所以加密以上2个语法元素不会破坏H.264/AVC编码的格式规范[8]。
式(11)和式(12)分别是对拖尾系数的符号位和非零系数的符号位的加密方法, 其中Key_C为1.3节生成的密钥。式(11)中的T1s表示拖尾系数的符号位, En_T1s为加密后的拖尾系数的符号位; 式(12)中的sign为非零系数的符号位, En_sign为加密后的非零系数的符号位。
运行加密算法的电脑配置了英特尔酷睿双核处理器(2.50 GHz), 内存为4 GB。视频编码运行的程序是H.264/AVC参考模型JM8.6版本主要档次。编码图像100帧, I帧间隔为5, P帧∶ B帧=1∶ 1, 量化系数(QP)设为18, 通过CAVLC编码模式分别编译视频Foreman、Calendar、Highway、Bus、City、Football、Harbour、Ice和Socce标准视频序列。视频序列的分辨率为Qcif(176* 144)和cifIF(352* 288)两种, 采样格式为4∶ 2∶ 0。
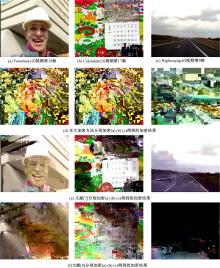
视频加密效果的主观测试方法[17]是通过观测者的肉眼对视频序列打分评测。选取Foreman(cif)的第19帧、Calendar(cif)的第17帧和Highway(qcif)的第9帧作为测试图像, 图9是本文加密方法和文献[7, 8]中的加密方法得到的加密图像, 从这3个视频序列的加密结果对比图中可以看出, 观众无法理解本文加密算法得到的加密图像, 加密图像满足了视频加密效果的主观测试安全需求。而且本算法明显优于文献[7]算法的加密效果, 虽然文献[8]的算法取得了较好的加密效果, 但对图像背景的干扰不及本文算法。
视频的主观评测需评测人员使用肉眼评测, 评测过程中可能因环境或者评测人员身体状况等因素导致评测结果的偶然性。为避免这种缺陷, 研究者提出了多种客观的视频质量评测方法, 包括峰值信噪比(PSNR)和结构相似性比较(SSIM)。
3.3.1 峰值信噪比比较分析
PSNR的计算公式为:
式中:MSE为原始图像与加密图像像素值之间的均方误差, 它被用来衡量原图像加密后的图像质量。
MSE的表达式为:
式中:
表2列出了8个不同的视频序列原始图像与使用本文加密算法加密后图像的PSNR对比结果。实验分别给出了Y、U、V三个分量PSNR的值。
| 表2 PSNR实验结果 Table 2 PSNR experimental result dB |
PSNR的数值越低说明视频的质量越差, 正常情况下当PSNR的数值低于15 dB时人眼就无法区分出视频内容[9]。表3列举了原视频序列和加密后的视频序列的PSNR, 表3中可见, 本文提出的视频加密方法加密后的视频图像PSNR数值均低于15 dB, 达到了预期的加密效果。表4对比了文献[79]所提方法和本文方法加密4种标准视频序列后的PSNR。本加密方法的PSNR平均值是13.42, 低于其他3种方法, 说明本加密方法的加密效果优于其他3种加密方法。
| 表3 PSNR对比 Table 3 Comparision of PSNR dB |
| 表4 不同QP下的PSNR Table 4 PSNR under different QP |
3.3.2 量化系数与PSNR
H.264/AVC编码时可在[0, 51]内根据实际需要灵活选择量化系数(QP), 当量化系数取最小值0时代表最精细的量化, 当QP取最大值51时代表最粗糙的量化。QP每增加6, Qstep增加1倍。
表4是Foreman视频序列在QP分别设置为18、24、30、36时的视频图像Y、U、V分量的PSNR值。表4可印证QP越小视频图像Y、U、V分量的PSNR值越高, 也表明视频质量越好。图10是在QP分别设置为18、24、30和36时, 本文方法加密Foreman视频序列的加密结果, 可以发现QP不同时得到的加密图像不同, 并且对加密效果影响很大。
 | 图10 QP=18, QP=24, QP=30, QP=36时的加密图像Fig.10 Encrypted images of QP = 18, QP = 24, QP = 30, and QP = 36, respectively |
3.3.3 结构相似性比较分析
SSIM是用来衡量两幅图像结构相似度的指标。SSIM取值范围为[0, 1], 数值越接近1说明两幅图像的相似度越高视频质量越好, 越接近0说明两幅图像相似度越低视频质量越差。SSIM的数值低于0.1时, 人眼就无法区分出视频内容[9]。SSIM的计算式为:
式中:x、y分别为原始视频图像和加密后的视频图像;
表5对比了本文加密方法和文献[7, 8, 9]所提方法加密不同视频序列的SSIM值, 本文加密方法得到的SSIM值均低于0.01, 表明人眼无法区分出加密视频的内容, 且优于文献[7, 8, 9]所提的方法。
| 表5 SSIM实验结果 Table 5 SSIM experimental result |
视频加密CAVLC编码过程中的T1s符号位、非零系数符号位和Exp-Golomb编码的信息位, 加密过程中只使用了简单的异或操作, 不但提高了加密的速度, 而且不影响视频编码格式和码长, 所以本文加密方法不影响视频的压缩比。
3.5.1 密钥空间
设混沌序列捕获区间为[1000, 10000], 按式(2)生成101组混沌序列, 前100组每组包括256个随机数值, 最后1组作为Logist的初值。根据Logist映射生成的索引, 从前100组混沌序列中选取2组, 将按位比较的结果作为密钥。由于密钥长度为256位, 所以密钥空间为100× 2256× 0.9× 103> 2274。表6中对比了本文和文献[7, 8, 12]的密钥空间, 本文加密方法的密钥空间高于文献[7, 8, 12]的密钥空间, 说明本文加密方法的密钥空间足够大, 可以抵挡唯密文攻击[15]。
| 表6 密钥空间对比 Table 6 Key space comparison |
3.5.2 密钥随机性检测
为检测密钥的随机性, 使用了NIST SP 800-22[18]软件测试了50万比特的密钥。密钥通过了NIST SP 800-22的全部16项测试, 见表7。这表明本文提出的密钥生成方案产生的密钥是随机的。
| 表7 NIST SP 800-22测试结果 Table 7 NIST SP 800-22 test results |
3.5.3 已知明文攻击
已知明文攻击是指攻击者掌握了某段明文和对应的密文后发起的攻击[9], 如MVD的符号位, 在编码过程中只有0和1这2个数值, 攻击者可通过不同的0和1数值序列替换加密位置的数值, 尝试对视频解密。图11是本文加密结果与对MVD的符号位使用已知明文攻击后的结果, 可发现已知明文攻击对本加密方法无效, 这说明本文提出的加密方法可以抵挡已知明文攻击。
3.5.4 推理攻击
推理攻击是指攻击者利用没有被加密的数据来推断出已经加密的数据[9], 为分析推理攻击的可能性, 分析了加密视频图像中像素的相关性。视频图像中相邻像素在垂直、左右和对角方向上都存在相关性, 正常解码得到的视频图像的相邻像素点在数值上十分接近, 而视频加密后将使图像像素之间的相关性降低。将图像像素的方差作为分析视频图像相关性的参数, 从表8中发现本文加密方法和文献[7]得到的像素值方差与正常解码图像像素值的方差相比都有较大改变, 且本文方法得到的方差比文献[7]的更大, 攻击者无法通过图像像素的相关性来解密加密后的视频图像。
| 表8 图像像素的方差 Table 8 Deviation value of image pixels |
基于混沌的视频加密算法加密延迟高的主要原因是:高维混沌产生混沌序列时计算复杂度高、耗费时间长、选择加密的数据过大和采用了复杂的加密运算。本文加密算法通过使用混沌序列池减少了求解高维混沌QCNN的次数, 同时只对视频关键语法元素加密, 有效减少了加密的数据量, 加密运算采用了运算速度快的异或运算, 显著降低了加密延迟。
从表9可看出, 随着编码帧数的增加, 文献[8]采用的加密方法编码延迟保持在1.32%到1.88%之间, 本文加密算法加密视频序列时编码10帧视频的延迟是2.76%, 但会随视频帧数的增加编码延迟逐渐降低, 当编码为70帧视频时, 延迟降低到了0.56%。这是由于初始生成混沌序列池时计算量较大, 当不再需要求解QCNN时, 随着编码帧数的增加, 加密的延迟就变得越来越小。虽然文献[7]的延迟小于本文和文献[8], 但在3.2节视频加密效果主观分析中发现, 文献[7]的加密效果并不理想。
| 表9 加密延迟分析, Foreman(qcif) Table 9 Encryption delay analysis, Foreman(qcif) |
本文提出了结合高维QCNN与低维Logistic混沌的密钥生成方案, 有效减少了QCNN的求解次数, 提高了密钥的生成速度。该方案的密钥空间为2274, 可抵挡已知明文攻击和推理攻击。视频加密算法只加密视频的T1s符号位、剩余非零系数的符号位和Exp-Golomb的INFO, 有效降低了视频加密的数据量, 且不改变视频的编码格式和视频的压缩比。仿真与实验对比表明, 本加密算加密效果好, 延迟小, 具有较好的安全性和应用价值。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|