引用本文
蔡振闹, 吕信恩, 陈慧灵. 基于反向细菌优化支持向量机的躯体化障碍预测模型[J].吉林大学学报（工学版）, 2018,48(3): 936-942
CAI Zhen-nao, LYU Xin-en, CHEN Hui-ling. Prediction model of somatization disorder based on an oppositional bacterial foraging optimization based support vector machine[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 936-942  
Doi:10.13229/j.cnki.jdxbgxb20170346
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有 吉林大学学报编辑部
基于反向细菌优化支持向量机的躯体化障碍预测模型
蔡振闹1, 吕信恩2, 陈慧灵3
1.西北工业大学 计算机学院,西安710072
2.温州大学 心理健康教育中心,浙江温州325035
3.温州大学 数理与电子信息工程学院,浙江 温州325035
通讯作者：吕信恩(1983-), 男, 讲师, 硕士.研究方向:心理健康教育,心理测量.E-mail:luxinen@163.com

作者简介:蔡振闹(1981-),男, 工程师, 博士研究生.研究方向:机器学习,数据挖掘.E-mail:erikcai@mail.nwpu.edu.cn

基金:浙江省自然科学基金项目(LY17F020012,Y14F020126); 温州市科技计划项目(ZG2017019).
摘要

基于改进的细菌优化算法(BFO)的支持向量机(SVM)提出了一种有效的智能预警模型(IBFO-SVM),并对社区矫正人员出现的躯体化障碍严重程度进行了预测。在IBFO-SVM 中,在细菌优化算法中引入反向学习策略,增加细菌种群的多样性,并使初始种群的个体尽可能均匀分布,提高BFO优化过程的收敛速度同时减少了BFO陷入局部最优解的概率。然后利用提出的反向细菌优化算法(IBFO)来确定SVM的两个最优参数(惩罚系数和核宽)。最后,将IBFO-SVM模型与基于原始细菌优化的SVM模型(BFO-SVM)、基于遗传算法的SVM模型(GA-SVM)以及基于粒子群优化算法的SVM模型(PSO-SVM)在心理评测数据上通过10折交叉验证方法进行了比较。实验结果表明:提出的IBFO-SVM预测模型在分类准确率、马修斯相关系数(MCC)、灵敏度和特异性方面比其他方法具有更好的性能,可以很好地将重度躯体化障碍和轻度躯体化障碍进行诊断。

关键词: 计算机应用; 躯体化障碍; 支持向量机; 反向学习; 细菌优化算法
中图分类号:TP393 文献标志码:A 文章编号:1671-5497(2018)03-0936-07
Prediction model of somatization disorder based on an oppositional bacterial foraging optimization based support vector machine
CAI Zhen-nao1, LYU Xin-en2, CHEN Hui-ling3
1.School of Computer Science and Engineering, Northwestern Polytechnical University, Xi'an 710072, China
2.Mental Health Education Center, Wenzhou University, Wenzhou 325035, China
3.College of Mathematics and Electronic Information Engineering, Wenzhou University, Wenzhou 325035, China
Abstract

The proposed Bacterial foraging optimization algorithm (BFO) based on support vector machine (SVM) presents an effective intelligent early-warning model (IBFO-SVM) for the somatization disorder severity prediction for Community Correction patients. In IBFO-SVM, opposition-based learning strategy is introduced into the BFO to increase the diversity of the bacterial population and uniformly distributed as far as possible for initial population, which improves the convergence rate of BFO and reduces the probability which falls into the local optimal solution. The proposed improved bacterial foraging optimization algorithm (IBFO) is used to determine the two optimal parameters of SVM (penalty coefficient and kernel width). For comparison purpose, the original BFO, genetic algorithm (GA), particle swarm optimization (PSO) has also been proposed to optimize the parameters of SVM. In this study, IBFO-SVM, BFO-SVM, GA-SVM and PSO-SVM model were compared by 10-fold cross-validation method in psychological evaluation data. The experimental results demonstrate that the proposed IBFO-SVM method has better performance in predicting the severe somatization disorder and mild somatization disorder in terms of classification accuracy, Mathews correlation coefficient (MCC), sensitivity and specificity than other methods.

Keyword: computer application; somatization disorder; support vector machine; opposition-based learning; bacterial foraging algorithm
0 引 言

20世纪中叶以来, 世界各国都在进行刑罚制度的革新, 探索更人性、更科学、更有效的刑罚方式来改善罪犯的心理与行为。社区矫正制度就是在这样的革新背景下产生的一种全新的刑罚方式。据统计, 当前, 中国社区矫正对象约有70万人。为了了解社区矫正对象的心理与行为特征, 评估社区矫正对象的心理健康水平, 一般采用症状自评量表(SCL-90)进行心理测量。在这些量表中, 体现躯体化(Somatization)障碍的因素有12项因素。躯体化因子主要反映主观的躯体不适感, 包括心血管、胃肠道、呼吸等系统的主述不适, 以及头疼、背痛、肌肉酸痛和焦虑的其他躯体表现。据调研发现, 目前人工智能技术在该方面的应用还鲜有报道, 刘怡桐[1]以中医人格特征为研究的切入点, 研究大学生心理健康的现状和影响因素。将神经网络运用于心理学研究人格特征与心理健康之间的关联性, 实验结果证实了大学生人格特征与心理健康存在显著的相关关系。时松和等[2]运用关联规则模型和神经网络模型研究南水北调中老年移民群体的心理干预效果及其心理健康、社会心理应激、社会支持的关系, 分析结果显示, 中老年移民的社会支持、心理社会应激以及心理健康有较强的关联性。

本文首次将提出的改进支持向量机方法应用于躯体化障碍的严重程度预测。为了提高区分社区矫正人员躯体化障碍的严重程度的评估准确率, 本文提出了一种基于反向细菌优化算法的支持向量机方法(Improved bacterial foraging optimization based support vector machine, IBFO-SVM)。作为一种主要的机器学习模式, 支持向量机(SVM)[3, 4] 基于VC维理论和结构风险最小化原理的基础上发展而来, 由于其独特的优势, SVM已经广泛地应用于一些分类任务[5, 6, 7, 8]。尤其是在计算机辅助医疗诊断上, SVM已经表现良好的诊断效果[7, 8, 9, 10, 11, 12, 13]。然而, SVM的性能主要受其模型中的参数所影响, 研究表明可通过建立适当的模型参数设置[14]大大提高其分类的准确性。因此, 关键参数应在其应用于实际问题之前设定为合适的值, 例如惩罚因子和核函数的核宽。传统方法上, 这些参数通过网格搜索方法[15]和梯度下降方法[16, 17, 18]来处理。然而, 这些方法容易陷入局部最优解。近来, 一些基于生物启发的元启发式搜索算法(如遗传算法(GA)[19]和粒子群优化算法(PSO)[20]), 相比上述传统的方法更容易找到全局最优解。

细菌优化算法(BFO)是Passino[21]于2002年基于大肠杆菌在人体肠道内吞噬食物的行为提出的一种新型仿生类算法, 它模仿了细菌觅食的趋向、聚群、复制和驱散等四种智能行为。该算法因具有群体智能算法并行搜索、易跳出局部极小值等优点, 成为生物启发式计算研究领域的又一热点, 并在很多领域获得了广泛应用。然而在优化的过程中, 细菌优化算法极其容易陷入局部最优, 很难找到全局最优解。针对这个问题, 本文将反向学习机制引入细菌优化算法, 提出一种改进的反向细菌优化算法(IBFO), 以改善种群多样性, 同时提高该算法的收敛速度。反向学习的原理是为每个初始候选解生成相对应的反向解, 并从候选解和相对应的反向解中选择适应度较优的解作为初始种群中的成员, 将有助于提高优化过程中的收敛速率。通过反向学习策略, 我们将在初始细菌种群中获取反向细菌种群, 增加了种群的多样性和使初始种群的个体尽可能均匀分布, 并有助于提高优化过程的收敛速度。然后将IBFO算法用于解决SVM的参数优化问题, 获得最优的模型(IBFO-SVM)。进而将该模型用于预测社区矫正人员的躯体化严重程度。实验中, 将IBFO-SVM与基于原始细菌优化的SVM模型(BFO-SVM)、基于遗传算法的SVM模型(GA-SVM)以及基于粒子群优化算法的SVM模型(PSO-SVM)在心理评测数据上通过10折交叉验证方法进行了比较。实验结果表明, 提出的IBFO-SVM预测模型在分类准确率、马修斯相关系数(MCC)、灵敏度和特异性方面比其他方法具有更好的性能。

1 预测模型的建立

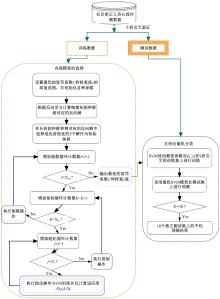
核心模型流程图如图1所示。

图1 基于反向细菌优化的支持向量机预测模型Fig.1 SVM prediction model based on oppositional BFO strategy

输入数据收集完成后, 对其进行10折交叉划分, 进而在训练数据集上采用基于反向学习的细菌优化算法对SVM的最优惩罚参数C和核宽 γ进行动态指定, 一旦完成训练, 最优参数将被送入SVM模型中执行预测任务。

在IBFO-SVM预测模型中, IBFO优化SVM参数的步骤如下:

步骤1 参数初始化, 包括:搜索空间维度为p、细菌种群规模大小为S、趋化循环次数为Nc、趋向性操作中在某一方向上的最大游泳次数为Ns、复制循环次数为Nre、驱散次数为Ned、驱散概率为Ped、趋向步长为c、初始化细菌种群的位置为P、C的搜索空间[Cmin, Cmax]和 γ的搜索空间[γ min, γ max]。

P(1, :, 1, 1, 1)=ub* rand(S, 1)'P(2, :, 1, 1, 1)=lb* rand(S, 1)'(1)

式中:ub为初始解的上限; lb为初始解的下限; rand(S, 1)'为S* 1矩阵的逆矩阵。

步骤2 根据反向学习策略, 计算细菌初始种群对应的反向解, 并从初始种群和对应的反向解中选择适应度较优的S个解作为初始种群。

步骤3 驱散循环loop: l=l+1

步骤4 复制循环loop: k=k+1

步骤5 趋化循环loop: j=j+1

(a)i=1, 2, …S, 细菌i进化趋化移动。

(b)计算适应度J(i, j, k, l), 该适应度基于细菌i当前位置的C和γ 值, 计算支持向量机的准确度ACC, 并将该值作为细菌i的适应度J(i, j, k, l)的值, 其中, ACC为基于K折交叉验证获取的平均准确度, 根据公式(2)计算, 其中acck表示每折计算的准确度。

ACC=∑k=1Kacck/K(2)

(c)让 Jlast=J(i, j, k, l)保存当前的适应度, 为了与以后迭代过程中得到的适应度进行比较; pbest保存当前细菌i的位置, pbest是一个维度为 1* 2的向量, 分别对应着C和γ 值, 以内部 K折交叉验证策略计算支持向量机的准确度ACC。

(d)翻转:按照式(3)进行翻转, 并计算新位置上的适应度函数值。

P(i, j+1, k, l)=P(i, j, k, l)+c(i)* ψ(i, j)(3)ψ(i, j)=Δ(i)/(ΔT(i)* Δ(i))1/2(4)

(e)计算新位置上的适应度函数值 J(i, j+1, k, l)。

(f)游动:如果细菌在新位置上的适应度函数值有所改善, 则计算趋向步长, 该细菌进行游动, 直到达到预定的最大趋向步数为止。

(g)如果i≠ S, 细菌(i+1)进化趋化移动。

步骤6 如果j< Nc, 跳转到步骤5, 继续进行趋化。

步骤7 复制:根据这次复制循环得到的适应度函数值的总和, 对所有的细菌进行排序, 拥有最高的Jhealth值的Sr个细菌死亡, 留下的Sr个最好值的细菌分裂开来, 结果放置在死亡细菌原先的父母的位置。

步骤8 如果k< Nre, 跳转到步骤4, 算法没有达到制定复制的数量, 所以, 开始下一次趋化循环, 产生后代。

步骤9 驱散:以概率Ped进行循环i=1, 2, …, S, 驱散每一个细菌, 保持持续不变的细菌种群数量。如果l< Ned, 跳转到步骤3, 否则结束。

2 实验设计
2.1 数据描述

本研究所获得的数据均来自温州市司法局下辖的司法所, 共抽取了419位社区矫正对象作为研究对象。这些研究对象主要是罪行轻微、主观恶性不大的服刑人员, 包括被判处管制的、被宣告缓刑的、被暂予监外执行的、被裁定假释的人员等。本研究采用了症状自评量表(SCL-90), 主要研究矫正对象在最近一周内的躯体化症状、抑郁、敌对、精神病性等10个方面的心理症状情况。其中, 躯体化症状主要反映主观的身体不适感, 共有12个特征属性。每个特征的取值范围为{1, 2, 3, 4, 5}, 分别表示没有、很轻、中度、偏重、严重等5种不同的症状。表1是12个特征属性的具体描述。

表1 特征属性描述 Table 1 Description of the data set
2.2 实验设置

为了验证所提出的IBFO-SVM算法, 将该算法与其他3种机器学习模型BFO-SVM, GA-SVM和PSO-SVM进行了详细对比。对于SVM, 采用LIBSVM工具包; 细菌优化算法、粒子群优化算法和遗传算法等算法采用MATLAB语言编程实现。实验环境采用MATLAB 2014b, 计算机配置如下:Windows 7操作系统, AMD Athlon 64 X2双核处理器(2.6 GHz)和 8 GB内存。

10折交叉验证用于划分数据样本, 保证分类结果的无偏差性。文中涉及方法的具体参数设置如下: IBFO, BFO, PSO和GA迭代次数和种群个数都统一分别被设置成50和8。参数搜索范围设置如下:C = {2-10, 2-8, …, 210} 并且 γ = {2-10, 2-8, …, 210}。BFO中趋向步长设为5, 游动步长设为4, 复制次数为5, 驱散次数为2, 驱散概率设为0.25。PSO中的最大速度vmax设置为每维的60%, 惯性权重设为1.4, 两个认知因子设为2。对于GA, 利用轮盘赌选择法选择父代染色体, 使用单点交叉法产生后代染色体, 采用均匀变异法改变染色体的属性值, 交叉概率设为0.8, 变异概率为0.04。

2.3 性能评估

为了评价提出的IBFO-SVM模型, 本文主要考察4个指标:分类准确率(ACC)、灵敏度 (Sensitivity)、特异性(Specificity) 和马修斯相关系数(MCC)。性能指标计算公式如下:

ACC=TP+TNTP+FP+FN+TN×100%(5)Sensitivity=TPTP+FN×100%(6)Specificity=TNFP+TN×100%(7)MCC=TP* TN-FP×FN(TP+FP)(TP+FN)(TN+FP)(TN+FN)×100%(8)

式中:TP为真阳性的数量, 即严重躯体化障碍个体被正确分类的个数; FN为误报的数量, 即严重躯体化障碍个体被分类成轻度躯体化障碍的个数; TN为真阴性的数量, 即轻度躯体化障碍被正确分类的个数; FP为假阳性的数量, 即轻度躯体化障碍被分类成严重躯体化障碍的次数。

3 实验结果与分析

之前的研究表明细菌优化算法中的趋向步长对细菌的搜索能力起到重要作用。因此本文首先对趋向步长对IBFO-SVM的性能影响进行了分析和研究。表2中显示了在不同趋向步长取值下IBFO-SVM在心理矫正数据上获得了分类结果。表中显示的数据主要是均值和方差构成。从表中可以看出, IBFO-SVM模型在趋向步长取值0.1时取得了最好的结果, 分别获得了95.47%的分类正确率, 马修斯相关系数为0.8999, 96.77%的灵敏性和92.86%的特异性。另外, 在取值为0.1时, 模型的方差也是最小, 这表明了在趋向步长取值为0.1时, 模型获得性能最稳定。因此, 在后续实验中, 本文将取趋向步长为0.1作为实验参数。

表2 不同趋向步长取值下IBFO-SVM的分类结果 Table 2 Classification results of IBFO-SVM with different chemotaxis step size

实验中, 本文评估了IBFO-SVM模型的有效性, 如表3所示, IBFO-SVM取得了平均95.47%的分类正确率, 马修斯相关系数为0.8999, 96.77%的灵敏性和92.86%的特异性。此外, 还可以观察到SVM的两个参数可由IBFO算法动态获得, 这主要归因于这两个参数可以由反向细菌优化算法根据训练数据的分布情况自适应地决定。

表3 IBFO-SVM在4个指标上的分类性能 Table 3 Classification performance of IBFO-SVM in terms of ACC, MCC, Sensitivity and Specificity

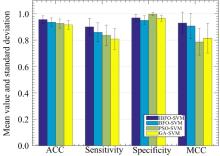
为了验证所提出方法的有效性, 将提出的方法与其他3种高效的机器学习模型包括BFO-SVM、GA-SVM和PSO-SVM进行对比研究。4种方法的对比曲线图如图2所示。从图中可以发

图2 IBFO-SVM, BFO-SVM, PSO-SVM和GA-SVM在ACC, MCC, Sensitivity和Specificity方面的分类性能比较Fig.2 Classification performance obtained by IBFO-SVM, BFO-SVM, PSO-SVM and GA-SVM in terms of ACC, MCC, Sensitivity, and Specificity

现IBFO-SVM模型在4个评价指标上都优于原始BFO-SVM模型, 而且方差也比原始BFO-SVM模型小, 说明IBFO-SVM模型与原始BFO-SVM模型相比不但性能更好而且更加稳定。

在ACC评价指标上, IBFO-SVM模型获得的结果最好。其次是BFO-SVM和PSO-SVM模型, GA-SVM模型获得的结果最差。在Sensitivity评价指标上, IBFO-SVM模型依然获得了最好的结果, 其次是BFO-SVM和PSO-SVM模型, GA-SVM模型获得的结果最差。在Specificity评价指标上, PSO-SVM模型获得的结果最好, 而且方差也是最小的, 其次是IBFO-SVM和GA-SVM模型, 原始BFO-SVM模型获得的结果最差。在MCC评价指标上, IBFO-SVM模型获得的结果最好, 而且方差也是最小的, 其次是BFO-SVM和GA-SVM模型, 原始PSO-SVM模型获得的结果最差。

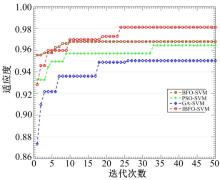
为了描述所提出的IBFO算法的收敛性, 本文在实验中也记录了各种模型获得的准确率随着种群迭代发生的变化趋势, 见图3。从图3中可以发现IBFO-SVM模型在训练的过程中可以快速地收敛到最佳精度, 说明IBFO算法具有较强的全局搜索能力, 可以避免算法过早地陷入局部最优。其中主要的原因在于反向学习策略起到了调节种群多样性的作用, 进而加快整个种群收敛到最优解。原始BFO-SVM模型在训练的过程中过早收敛导致无法获得更高的精度。GA算法的搜索能力最弱, 导致GA-SVM模型获得最差的精度。

图3 IBFO-SVM, BFO-SVM, PSO-SVM和GA-SVM 获得的适应度跟迭代次数之间的关系Fig.3 Relationship between the iteration and fitness of IBFO-SVM, BFO-SVM, PSO-SVM and GA-SVM

4 结束语

本文提出了一种基于反向细菌优化算法的支持向量机模型对社区矫正人员的心理状况进行辅助诊断。本文的主要创新点在于提出基于反向学习的细菌优化算法, 基于该方法SVM可以获得更优的参数, 进而获得更高的预测性能。实验结果表明, 在心理评测数据集上, 本文提出的IBFO-SVM模型与其他三种先进的SVM模型相比, 在分类准确率、马修斯相关系数、灵敏度和特异性方面均具有更好的性能。因此, 本文提出的智能预警模型可以提前为社区矫正人员发生躯体化障碍的严重程度发出预警, 进而为防止该类人员发生躯体化障碍提供辅助作用。

The authors have declared that no competing interests exist.

参考文献
[1] 刘怡桐. 大学生五态人格和心理健康的相关性研究[D]. 北京: 北京中医药大学, 2011.
Liu Yi-tong. Correlation study between five-pattern personality and mental health of college Students[D]. Beijing University of Chinese Medicine, 2011. [本文引用:1]
[2] 时松和, 冯邵珍, 张智民, 等. 南水北调中老年移民心理干预效果分析[J]. 现代预防医学, 2016, 43(6): 1051-1056.
Shi Song-he, Feng Shao-zhen, Zhang Zhi-min, et al. Analysis of the effect of psychological intervention among middle-aged and elderly immigrants in South-to-North Water Transfer Project[J]. Modern Preventive Medicine, 2016, 43(6): 1051-1056. [本文引用:1]
[3] Boser B E, Guyon I M, Vapnik V N. A training algorithm for optimal margin classifiers[C]∥Proceedings of the fifth annual workshop on Computational learning theory, ACM, 1992: 144-152. [本文引用:1]
[4] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer, 2000: 138-167. [本文引用:1]
[5] Aslahi-Shahri B M, et al. A hybrid method consisting of GA and SVM for intrusion detection system[J]. Neural Computing and Applications, 2016, 27(6): 1669-1676. [本文引用:1]
[6] Chen P, Yuan L, He Y, et al. An improved SVM classifier based on double chains quantum genetic algorithm and its application in analogue circuit diagnosis[J]. Neurocomputing, 2016, 211: 202-211. [本文引用:1]
[7] Shahdoosti H R, Hazavei S M. Combined ripplet and total variation image denoising methods using twin support vector machines[J]. Multimedia Tools & Applications, 2017 (12) : 1-19. [本文引用:2]
[8] Chen H L, Yang B, Liu J, et al. A support vector machine classifier with rough set-based feature selection for breast cancer diagnosis[J]. Expert Systems with Applications, 2011, 38(7): 9014-9022. [本文引用:2]
[9] Übeyli E D. Comparison of different classification algorithms in clinical decision-making[J]. Expert Systems, 2010, 24(1): 17-31 [本文引用:1]
[10] Chen H L, Yang B, Wang G, et al. A three-stage expert system based on support vector machines for thyroid disease diagnosis[J]. Journal of Medical Systems, 2012, 36(3): 1953-1963. [本文引用:1]
[11] Chen H L, Bo Y, Gang W, et al. Support vector machine based diagnostic system for breast cancer using swarm intelligence[J]. Journal of Medical Systems, 2012, 36(4): 2505-2519. [本文引用:1]
[12] Li M, Chen W, Zhang T. Automatic epilepsy detection using wavelet-based nonlinear analysis and optimized SVM[J]. Biocybernetics & Biomedical Engineering, 2016, 36(4): 708-718. [本文引用:1]
[13] Ye F. Evolving the SVM model based on a hybrid method using swarm optimization techniques in combination with a genetic algorithm for medical diagnosis[J]. Multimedia Tools & Applications, 2016: 1-30. [本文引用:1]
[14] Keerthi S, Lin C. Asymptotic behaviors of support vector machines with Gaussian kernel[J]. Neural Computation, 2003, 15(7): 1667-1689. [本文引用:1]
[15] Chang C C, Lin C J. LIBSVM: a library for support vector machines[M]. ACM, 2011. [本文引用:1]
[16] Gold C, Sollich P. Model selection for support vector machine classification[J]. Neurocomputing, 2003, 55(1/2): 221-249. [本文引用:1]
[17] Keerthi S. Efficient tuning of SVM hyperparameters using radius/margin bound and iterative algorithms[J]. IEEE Transactions on Neural Networks, 2002, 13(5): 1225-1229. [本文引用:1]
[18] Chapelle O. Choosing multiple parameters for support vector machines[J]. Machine Learning, 2002, 46(1): 131-159. [本文引用:1]
[19] Huang C L, Wang C J. A GA-based feature selection and parameters optimizationfor support vector machines[J]. Expert Systems with Applications, 2006: 31(2): 231-240. [本文引用:1]
[20] Chen H L, Yang B, Wang S J, et al. Towards an optimal support vector machine classifier using a parallel particle swarm optimization strategy[J]. Applied Mathematics & Computation, 2014, 239(8): 180-197. [本文引用:1]
[21] Passino K M. Biomimicry of bacterial foraging for distributed optimization and control[J]. IEEE Control Systems Magazine, 2002, 22(3): 52-67. [本文引用:1]