基于空间矢量模型的图像分类方法

引用本文

陈绵书, 苏越, 桑爱军, 李培鹏. 基于空间矢量模型的图像分类方法[J].吉林大学学报（工学版）, 2018,48(3): 943-951
CHEN Mian-shu, SU Yue, SANG Ai-jun, LI Pei-peng. Image classification methods based on space vector model[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 943-951 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170444
Permissions

基于空间矢量模型的图像分类方法

陈绵书, 苏越, 桑爱军, 李培鹏

吉林大学通信工程学院, 长春 130022

作者简介:陈绵书(1973-),男,副教授,博士.研究方向:图像处理,人工智能.E-mail:chenms@jlu.edu.cn

基金:吉林省国际科技合作项目(20130413053GH).

摘要

针对词袋模型视觉单词没有考虑空间信息的不足,提出了一种基于视觉单词间空间位置信息的空间矢量模型。该模型利用视觉单词的空间位置信息,采用图像空间矢量模型对图像进行表述,从而达到了更好的分类效果。实验在两个标准图像数据集Caltech-101和Caltech-256上进行,分别采用支持向量机(SVM)和K最近邻分类器(KNN)对其进行分类。实验表明,空间矢量模型有效地提高了平均分类正确率(ACA)和平均类别准确率(ACP),具有很好的分类效果。

关键词: 信息处理技术; 图像分类; 空间矢量模型; 词袋模型; 矢量矩阵

中图分类号:TP391.4 文献标志码:A 文章编号:1671-5497(2018)03-0943-09

Image classification methods based on space vector model

CHEN Mian-shu, SU Yue, SANG Ai-jun, LI Pei-peng

College of Communication Engineering, Jilin University, Changchun 130022, China

Abstract

A space vector model is proposed to overcome the lack of spatial location information in the bag-of-words model. The model turns visual words into vector model using the space location information of visual words to represent image, thereby achieves better classification performance. Experiments are carried out on two standard image datasets Caltech-101 and Caltech-256, respectively, with Support Vector Machine (SVM) and K-Nearest Neighbor (KNN) classifiers. The results show that the space vector model can effectively improve the Average Classification Accuracy (ACA) and Average Category Precision (ACP), and has a good classification effect.

Keyword: information processing technology; image classification; space vector model; bag-of-words model; vector matrix

文章图片

0 引言

随着互联网中图像数量的急速增长, 如何准确且快速地对图像进行分类显然已经成为了一个热门领域。而源自于文本领域的图像分类模型— 词袋模型(Bag-of-words, BOW)^[1]作为一种信息检索算法, 在文本分类领域有着广泛的应用。BOW模型忽略掉一个文档的结构、语法和语序等, 仅仅将其看作是若干个独立单词的集合, 文档中任意位置出现的单词, 均不受该文档的语义影响而单独存在。将这一原理与图像相结合, 认为图像是由一些相互无关联的视觉单词组成。具体的做法为:先提取图像的SIFT^{[2, 3]}(Scale-invariant feature transform)特征, 之后把视觉特征转换为一系列的图像视觉单词, 最后, 根据每一个视觉单词在图像中出现的概率来绘制直方图。视觉单词出现的频率越高, 相应的概率值就越大。因此, 词袋模型不仅具有文本匹配高效简洁的特点, 而且原理简单, 易于编程和实际操作。然而, 词袋模型没有考虑到视觉单词之间的空间位置信息。研究表明, 视觉单词间的空间位置信息有助于提高图像的表述能力。Lazebnik等^[4]利用金字塔匹配核函数, 提出了SPM模型(Spatial pyramid matching); Wu等^[5]提出了视觉语言模型(Visual language model, VLM); Jiang等^[6]利用随机划分图像来提高分类性能。然而以上研究均没有考虑到全局信息, 且存在大量冗余的短语信息, 从而严重地影响到计算速率。考虑以上不足, 本文提出了一种基于视觉单词间空间位置信息的空间矢量模型。

1 空间矢量模型

在以往的图像分类应用中, BOW模型取得了不错的分类效果。但是在这些应用中, 均是将单词视为独立的存在, 彼此间没有联系且完全独立。可事实上, 通常一幅图像中出现的单词都是有结构联系的, 不可能完全独立, 所以这种单词之间完全独立的假设显然不成立。由此, 这里提出了结合视觉单词空间信息的图像分类方法。实验结果表明, 这种方法能够有效地提高图像分类的平均分类正确率(Average classification accuracy, ACA)和平均类别准确率(Average category precision, ACP)。

1.1 构建空间矢量模型

对图像进行SIFT特征提取、聚类, 以生成视觉单词。然后利用视觉单词的空间位置信息, 将图像表达为空间位置模型。对于一幅图像来说, 其表示为:

$\begin{array}{l} I = {(w_{1}, x_{1}, y_{1}), (w_{2}, x_{2}, y_{2}), \\ \dots, (w_{m}, x_{m}, y_{m})} (1) \end{array}$

式中: $w$ 为图像经过聚类表达后得到的视觉单词; $m$ 为视觉单词的个数; $(x, y)$ 为单词坐标位置。

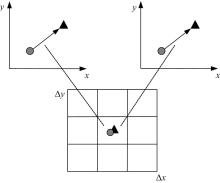
这里需明确两个重要的问题:①视觉单词之间的联系是什么; ②应该怎样准确地表达这种联系。空间位置矩阵最大的问题就是不包含视觉单词之间的空间位置信息。考虑到视觉单词的空间关系, 两两视觉单词能够构成矢量, 形成一对单词对。这样一来图像就能够映射成空间矢量矩阵。如图1所示, 设CUP图像提取出3个视觉单词分别为 $w_{1} 、 w_{2} 、 w_{3},$ 其中两两之间能够构成一个矢量, 所以一共可以得到3个矢量, CUP图像的空间矩阵表达式就可以表示为矢量的形式:

	Figure Option View Download New Window
	图1 空间位置模型与空间矢量模型Fig.1 Spatial position model and space vector model

$\begin{array}{l} M = {(w_{1}, w_{2}, x_{2} - x_{1}, y_{2} - y_{1}), \\ (w_{1}, w_{3}, x_{3} - x_{1}, y_{3} - y_{1}), \\ (w_{2}, w_{3}, x_{3} - x_{2}, y_{3} - y_{2})} (2) \end{array}$

同理, 如果一幅图像的视觉单词有 $η$ 个, 则最终得到 $C_{η}^{2}$ 个矢量。具体的表达式为:

$\begin{array}{l} M = {(w_{1}, w_{2}, x_{2} - x_{1}, y_{2} - y_{1}), \\ (w_{1}, w_{3}, x_{3} - x_{1}, y_{3} - y_{1}), \dots, \\ (w_{m - 1}, w_{m}, x_{m} - x_{m - 1}, y_{m} - y_{m - 1})} (3) \end{array}$

式中: $m 为单词的个数; w$ 为视觉单词。

将图像表示为空间矢量矩阵后, 虽然考虑到了视觉单词之间的联系, 但仍有两个问题有待商榷。

(1)如何构建一个合理的空间矢量模型。对于一幅图像, 可以获得大量空间矢量, 而其中只有非常有限的矢量是有关的。由于需要的视觉单词对是该幅图像与其他图像共同出现的单词对, 所以可以通过对比该幅图像的所有矢量与其他图像矢量的距离来选取有关矢量。若两个矢量间的距离大于某一阈值, 就将该矢量舍弃, 反之, 则保留。不过这种方法显然需要很大的计算量。假设两幅图像分别有 $m_{1} 和 m_{2}$ 个视觉单词, 那么计算复杂度就是 $O (C_{m_{1}}^{2} \times C_{m_{2}}^{2}), 若是有 N$ 幅图像, 那么计算复杂度将会急速增长。可以通过空间矢量量化的方法解决这一问题, 即将空间矢量网格化, 如图2所示。若两个矢量相关, 那么 $(x'_{1} - x_{1}, y'_{1} - y_{1}) 与 (x'_{2} - x_{2}, y'_{2} - y_{2})$ 就会落在同一格中。

	Figure Option View Download New Window
	图2 矢量位移对比Fig.2 Comparison of vector displacement

(2)如何利用空间矢量模型进行分类。本文使用支持向量机(Support vector machine, SVM)^[7]和K最近邻分类器(K-nearest neighbor, KNN)^[8]对图像进行分类, 分别提出两种不同的分类方法。

1.2 构建有效的空间矢量矩阵

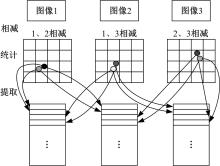
图3为有效空间矢量矩阵的构建过程图, 具体包括以下4个步骤。

	Figure Option View Download New Window
	图3 有效空间矢量矩阵的构建Fig.3 Structure of valid space vector matrix

(1)相减

将图像库中不同图像间相同的单词空间位置两两相减。这里假定有分别包含 $m$ 个视觉单词和n个视觉单词的两幅图像 $I_{1}$ 和 $I_{2}$ , 空间位置矩阵分别为 $d_{1}$ 和 $d_{2}$ 。则它们的空间位置差矩阵为:

$\begin{array}{l} s (d_{1}, d_{2}) = \overset{m}{⋃_{i = 1}} \overset{n}{⋃_{j = 1}} φ (d_{1_{i}}, d_{2_{j}}) (4) \\ φ (d_{1_{i}}, d_{2_{j}}) = \{\begin{array}{l} (w_{i}, x_{j} - x_{i}, y_{j} - y_{i}), w_{i} = w_{j} \\ 0, w_{i} \neq w_{j} \end{array} (5) \end{array}$

式中: $d_{1} = {(w_{a}, x_{a}, y_{a}), (w_{b}, x_{b}, y_{b}), \dots, (w_{m}, x_{m}, y_{m})}; d_{2} = {(w_{a}, x_{a_{1}}, y_{a_{1}}), (w_{a}, x_{a_{2}}, y_{a_{2}}), \dots, (w_{n}, x_{n}, y_{n})} 。$

假设 $I_{1}$ 中第一个视觉单词为 $w_{a}, I_{2}$ 中有2个与 $w_{a}$ 相同的单词。依据式(5)就可以得到位移点的坐标 $(x_{a_{1}} - x_{a}, y_{a_{1}} - y_{a}) 和 (x_{a_{2}} - x_{a}, y_{a_{2}} - y_{a}) 。$ 之后再将第1幅图像中的单词与第2幅图像中的所有单词进行比较, 就能够得出 $I_{1} 与 I_{2}$ 的空间位置差矩阵。其中, 空间位置差矩阵中的每条记录都包含信息 $(w_{1}, x_{1} - x_{2}, y_{1} - y_{2})$ 。其中 $w_{1}$ 表示视觉单词; $x_{1}$ 和 $y_{1}$ 为单词在图像 $I_{1}$ 中的坐标; $x_{2}$ 和 $y_{2}$ 为单词在图像 $I_{2}$ 中的坐标。

(2)统计

假设某网格中有n个点, 若n=2, 那么视觉单词对的个数为1; 若n< 2, 那么视觉单词对的个数为0; 若n> 2, 那么单词对的个数为 $C_{n}^{2} 。$

(3)提取

提取单词对个数不小于2的点, 并保存到对应的空间矢量矩阵中。假设 $I_{1}$ 与 $I_{2}$ 的空间矢量矩阵分别为 $M_{1}$ 和 $M_{2}$ , 若空间位置差矩阵在某一个网格内存在2个点 $w_{1}$ 和 $w_{2}$ , 那么:

$\begin{array}{l} M_{1} (1, :) = (w_{1}, w_{2}, x_{_{2}}^{I_{1}} - x_{_{1}}^{I_{1}}, y_{_{2}}^{I_{1}} - y_{_{1}}^{I_{1}}) \\ (6) \\ M_{2} (1, :) = (w_{1}, w_{2}, x_{_{2}}^{I_{2}} - x_{_{1}}^{I_{2}}, y_{_{2}}^{I_{2}} - y_{_{1}}^{I_{2}}) \\ (7) \end{array}$

同理, 将 $(I_{1}, I_{2})$ 空间位置差相同的点全部提取出来。

以此类推, 依次提取 $(I_{1}, I_{3}), (I_{1}, I_{4}), \dots, (I_{2}, I_{3}), (I_{2}, I_{4}), \dots, (I_{N - 1}, I_{N})$ 中空间位置差值相同的点。

(4)消除重复

由于总会出现某一图像的矢量与其他图像相同的情况, 所以需要去除 $M_{1}, M_{2}, M_{3}, \dots, M_{N}$ 中的重复行, 这样的操作能够剔除不相关的矢量, 以保证得到的空间矢量矩阵能最有效地代表图像的空间信息。

2 基于SVM和KNN的图像分类

2.1 基于SVM的图像分类

基于SVM分类器的图像分类包括3个步骤:建立视觉短语库、图像表达和分类判决。

2.1.1 建立视觉短语库

训练集图像的视觉单词经过空间矢量转化后, 每一幅图像都会表示成一个 $N \times 4$ 的空间矢量矩阵。使用K均值聚类将距离比较近的4维矢量合并。为了简化, 这里假设K值为3, 具体的视觉短语库的构建过程如图4所示。

	Figure Option View Download New Window
	图4 视觉短语库构造过程Fig.4 Structure of visual phrase lexicon

2.1.2 图像表达

假设一个 $N \times 4$ 的图像空间矢量矩阵, 计算每个矢量到视觉短语的距离, 若与某一个视觉短语最近, 就将这个短语的bin值加1。从而完成视觉短语直方图的转化, 归一化之后称为视觉短语特征。最后, 将视觉短语直方图与视觉单词直方图结合, 形成视觉语言直方图。这样, 视觉语言模型不仅考虑到了全局信息, 也包含空间特征。

视觉语言模型的主要原理包括:

(1)对2个特征集 $X 、 Y,$ 将其划为L个层(L=2, 层1和层2分别为视觉单词直方图和视觉短语直方图)。

(2)在层 $l 中, 若点 x, y$ 落入同一bin中, 就称x与y匹配。每个bin中匹配点的个数为 $\min (X_{i}, Y_{i})$ , 其中 $X_{i}, Y_{i}$ 为相应层下的第 $i$ 个bin。

(3) $H_{X}^{l} 、 H_{Y}^{l}$ 分别为 $X 、 Y$ 在层l中的直方图特征, $H_{X}^{l} (i) 、 H_{Y}^{l} (i)$ 分别为层 $l$ 中 $X 、 Y$ 落入第 $i$ 个bin的特征点的个数, 那么在 $l$ 层下匹配点的总数为:

$I (H_{X}^{l}, H_{Y}^{l}) = \overset{D}{\sum_{i = 1}} \min (H_{X}^{l} (i), H_{Y}^{l} (i)) (8)$

在后文中, 把 $I (H_{X}^{l}, H_{Y}^{l})$ 简写成 $I^{l}$ 。

(4)统计每层 $l$ 下的匹配点的总数 $I^{l}$ , 不同的 $l$ 赋予不同的权重 $w$ 。

(5)两个点集 $X 、 Y$ 匹配程度的匹配核为:

$K^{L} (X, Y) = \overset{L}{\sum_{i = 1}} w_{i} I^{l} (9)$

式中: $\overset{L}{\sum_{i = 1}}$ w_i=1。

视觉语言模型的构建过程主要包括以下两个步骤。

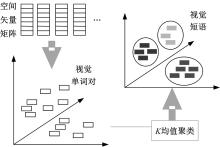
(1)如图5所示, 对图像特征聚类映射后, 提取视觉单词直方图。之后将视觉单词转化为空间矢量矩阵, 提取视觉短语直方图, 如图6所示。

	Figure Option View Download New Window
	图5 视觉单词直方图Fig.5 Histogram of visual words

	Figure Option View Download New Window
	图6 视觉短语直方图Fig.6 Histogram of visual phrase

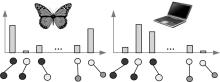
(2)将两个层的直方图首尾连接, 同时赋予每个层相应的权重, 如图7所示。

	Figure Option View Download New Window
	图7 视觉语言直方图Fig.7 Histogram of visual language

2.1.3 分类判决

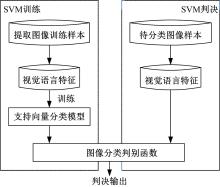
基于SVM分类器的具体训练和判决过程如图8所示。

	Figure Option View Download New Window
	图8 SVM分类器过程图Fig.8 Flow diagram of SVM classification

2.2 基于KNN的图像分类

根据KNN分类原理, 利用空间矢量矩阵对图像进行分类:首先, 对所有训练图像的空间矢量矩阵进行量化; 然后, 设 $M$ 为测试图像X的空间矢量矩阵, 统计它与 $(M_{1}, M_{2}, \dots, M_{N})$ 中相同行的个数; 最后, 利用相同个数最多的K个样本来判断测试图像X的标签。

2.2.1 量化统计

首先, 分别对 $x$ 方向及y方向的矢量差进行量化, 量化间隔设为3; 然后, 计算两幅图像具有相同行的个数:

$\begin{array}{l} Num = \overset{N_{1}}{\sum_{i = 1}} \overset{N_{2}}{\sum_{j = 1}} φ (M_{i}^{1}, M_{j}^{2}) (10) \\ φ (a, b) = \{\begin{array}{l} 1, a = b \\ 0, a \neq b \end{array} (11) \end{array}$

式中: $N_{1} 、 N_{2}$ 分别为空间矢量矩阵 $M^{1}$ 和 $M^{2}$ 的记录行数。

2.2.2 参数选取

(1) $K$ 值的选取

本文利用交叉验证法(cross-validate)^{[9, 10]}选取最佳 $K$ 值。

(2)权重的选取

如果认定各特征的权重都相同, 那么会大大降低图像的分类效果。本文利用与测试图像的空间矢量矩阵相同行的数量来分配权重。然后将权重累加, 选定累加值最高的类别作为样本的类别标签。

将相同行个数的平方值作为权重。设训练数据集包含2个标签, $K$ 个近邻中有 $K_{1}$ 个作为标签1, $K_{2}$ 个作为标签2 $(K_{1} + K_{2} = K),$ 则判为标签1的概率为:

$P'_{1} = \frac{K_{1}}{K} (12)$

取权重后的概率为:

$P_{1} = \frac{\overset{K_{1}}{\sum_{i = 1}} L_{1 i}^{2}}{\overset{K_{1}}{\sum_{i = 1}} L_{1 i}^{2} + \overset{K_{2}}{\sum_{i = 1}} L_{2 i}^{2}} (13)$

判为标签2的概率为:

$P'_{2} = \frac{K_{2}}{K} (14)$

取权重后的概率为:

$P_{2} = \frac{\overset{K_{2}}{\sum_{i = 1}} L_{2 i}^{2}}{\overset{K_{1}}{\sum_{i = 1}} L_{1 i}^{2} + \overset{K_{2}}{\sum_{i = 1}} L_{2 i}^{2}} (15)$

式中: $L_{1} 和 L_{2}$ 分别为测试图像与标签1和标签2的训练图像空间矢量矩阵相同行的数量。

2.2.3 分类判决

通过参数的选取, 确定了基于词袋模型的最佳K值(K_B)和基于空间矢量矩阵的最佳K值(K_M)。这里假定训练集包括2个标签, 那么对于一幅测试图像, 判为标签1的概率为:

$P_{1} = \frac{K_{B}}{K_{B} + K_{M}} P_{1 Bow} + \frac{K_{M}}{K_{B} + K_{M}} P_{1 Mat} (16)$

判为标签2的概率为:

$P_{2} = \frac{K_{B}}{K_{B} + K_{M}} P_{2 Bow} + \frac{K_{M}}{K_{B} + K_{M}} P_{2 Mat} (17)$

比较式(16)和式(17)的大小, 将概率值相对较高的标签作为最终测试图像的分类类别。

3 旋转不变性

在图像分类中, 有些发生旋转的图像会对分类效果造成影响。如图9所示, 为了消除这种影响, 本文提出了矢量模的方法。由于两两单词构成一个矢量, 所以当图像旋转时, 矢量的长度不变。因此对于一个 $N \times 3$ 的图像矩阵, 具体的表达式为:

	Figure Option View Download New Window
	图9 图像旋转的分析Fig.9 Analysis of image rotation

$\begin{array}{l} M = {(w_{1}, w_{2}, \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}), \dots, \\ (w_{m - 1}, w_{m}, \sqrt{(x_{m} - x_{m - 1})^{2} + (y_{m} - y_{m - 1})^{2}})} (18) \end{array}$

在构建有效的空间矢量矩阵后, 分别利用KNN和SVM分类器进行分类。

4 实验及结果讨论

本次实验在Caltech 101数据集和Caltech 256数据集中^[11]分别选取8个类别, 并将数据集分为测试图像和训练图像两部分。从Caltech 101数据集中取8个类别的图像(Faces_easy、向日葵、摩托车、蝴蝶、笔记本电脑、双栀船、盆景、袋鼠)进行分类实验, 实验分为二类类别(Faces_easy、向日葵)、四类类别(Faces_easy、向日葵、摩托车、蝴蝶)、六类类别(Faces_easy、向日葵、摩托车、蝴蝶、笔记本、双栀船)和八类类别(Faces_easy、向日葵、摩托车、蝴蝶、笔记本、双栀船、盆景、袋鼠); 从Caltech 256数据集取8个类别的图像(ak47、双筒望远镜、骆驼、鸭子、烟火、三角钢琴、火星、网球鞋)进行分类实验, 实验分为二类类别(ak47、双筒望远镜)、四类类别(ak47、双筒望远镜、骆驼、鸭子)、六类类别(ak47、双筒望远镜、骆驼、鸭子、烟火、三角钢琴)和八类类别(ak47、双筒望远镜、骆驼、鸭子、烟火、三角钢琴、火星、网球鞋), 所有实验都重复10次取其统计平均, 并对结果进行分析。评价标准采用平均分类正确率(ACA)和平均类别准确率(ACP)。

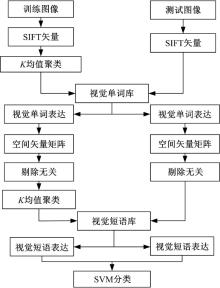
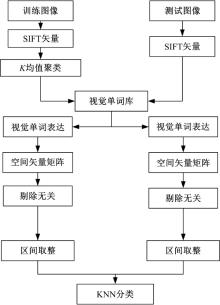
这里分别基于词袋模型、空间金字塔、空间矢量模型(SpVM)、具有旋转不变性的空间矢量模型(SpVM-ROT)进行实验, 实验过程分别如图10和图11所示。

	Figure Option View Download New Window
	图10 基于SVM分类的框架图Fig.10 Frame diagram of classification based on SVM

	Figure Option View Download New Window
	图11 基于KNN分类的框架图Fig.11 Frame diagram of classification based on KNN

4.1 基于SVM的分类

4.1.1 参数的选择

(1)网格间距的选择

网格间距的选择对最终的分类结果有很大的影响。若网格间距太小, 那么落入同一网格的单词会很少, 获得的样本太少; 若网格间距太大, 那么落入同一网格的单词会很多, 缺乏了准确性。所以选择一个合适的网格间距尤为重要。这里经验性地选择间距为3。

(2)权重的选择

视觉语言直方图分为两层:1层是视觉单词直方图; 2层是视觉短语直方图。两层的权重分别为 $w_{1} 和 w_{2} 。$ 经过比较实验, 取w₁=0.4, w₂=0.6。

(3)聚类 $K$ 的选择

本文设置不同的 $K$ 值, 分析视觉短语库大小对分类性能的影响。其中, 二类分类的 $K$ 值为500; 四类分类的 $K$ 值为800; 六类分类的 $K$ 值为1400; 八类分类的 $K$ 值为2000。

4.1.2 实验结果

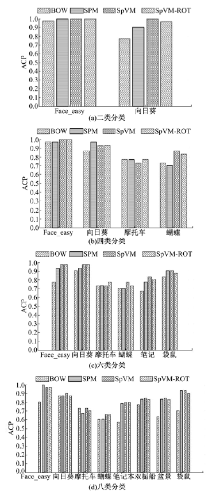
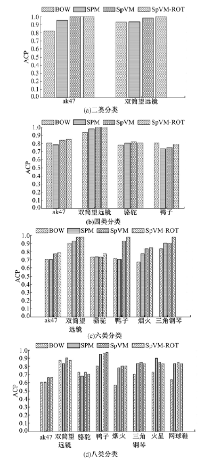
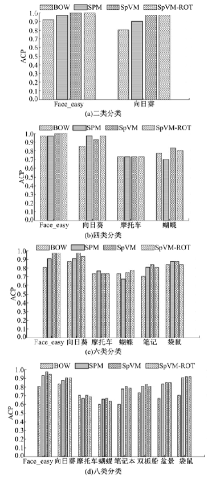
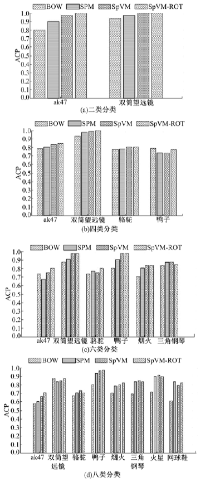
Caltech-101数据集和Caltech-256数据集的ACA和ACP分类结果分别如表1、表2和图12、图13所示。

表1 Caltech-101基于SVM的平均分类正确率 Table 1 ACA in Caltech-101 data collection based on SVM %

表2 Caltech-256基于SVM的平均分类正确率 Table 2 ACA in Caltech-256 data collection based on SVM %

	Figure Option View Download New Window
	图12 Caltech-101基于SVM的平均类别准确率Fig.12 ACP in Caltech-101 data collection based on SVM

	Figure Option View Download New Window
	图13 Caltech-256基于SVM的平均类别准确率Fig.13 ACP in Caltech-256 data collection based on SVM

4.2 基于KNN分类器的分类

4.2.1 参数的选择

通过交叉验证选择 $K$ 值, 选用相同记录个数的平方作为权重。

4.2.2 实验结果

Caltech-101数据集和Caltech-256数据集的ACA和ACP分类结果分别如表3、表4和图14、图15所示。

表3 Caltech-101基于KNN的平均分类正确率 Table 3 ACA in Caltech-101 data collection based on KNN %

表4 Caltech-256基于KNN的平均分类正确率 Table 4 ACA in Caltech-256 data collection based on KNN %

	Figure Option View Download New Window
	图14 Caltech-101基于KNN的平均类别准确率Fig.14 ACP in Caltech-101 data collection based on KNN

	Figure Option View Download New Window
	图15 Caltech-256基于KNN的平均类别准确率Fig.15 ACP in Caltech-256 data collection based on KNN

4.3 实验结果分析

这里对分类错误的图像进行统计和分析。如图16所示, 分类错误的图像主要包括两类:一是受光照影响较大的图像, 可以考虑通过图像滤波或图像增强等对图像进行预处理; 二是背景较为杂乱或者物体本身绘有花纹的图像, 这类影响具有不可避免性, 所以如何避免此类干扰的影响, 从而提高分类效果, 将是下一步研究的重点。另外, 当考虑旋转不变性时, 有些分类准确率会出现不升反降的现象, 这种现象主要发生在Caltech 101数据集上。这是因为Caltech 101数据集中很少有发生旋转的图像, 图像都相对简单, 从而导致聚类后的视觉单词对之间难以分辨; 而在图像数据复杂的Caltech 256数据集上则表现良好。

	Figure Option View Download New Window
	图16 错误分类图像示例Fig.16 Misclassification image samples

5 结束语

提出了一种基于视觉单词间空间位置信息的空间矢量模型, 并基于两种分类器提出了不同的分类方法:当使用SVM分类时, 将空间矢量矩阵转化为视觉语言模型, 利用视觉语言直方图特征进行分类; 当使用KNN分类时, 利用空间矢量矩阵具有相同行的个数, 通过选择最佳的 $K$ 值和权重进行分类。最后, 对本文提出的基于空间矢量模型的图像分类方法进行了对比实验。实验结果显示, 本文方法具有很好的分类效果。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Li Fei-fei. Visual recognition: computational models and human psychophysics[D]. Pasadena: College of Electronic Engineering, California Institute of Technology, 2005. [本文引用:1]
[2]	刘佳, 傅卫平, 王雯, 等. 基于改进SIFT算法的图像匹配[J]. 仪器仪表学报, 2013, 34(5): 1107-1112. Liu Jia, Fu Wei-ping, Wang Wen, et al. Image matching based on improved sift algorithm[J]. Chinese Journal of Scientific Instrument, 2013, 34(5): 1107-1112. [本文引用:1]
[3]	生海迪. 视觉词袋模型的改进及其在图像分类中的应用研究[D]. 济南: 山东师范大学信息科学与工程学院, 2015. Sheng Hai-di. The improvement of bag-of-visual-words model and its application research in images classification[D]. Ji'nan: College of Information Science and Engineering, Shand ong Normal University, 2015. [本文引用:1]
[4]	Lazebnik S, Schmid C, Ponce J. Beyond bags of features: spatial pyramid matching for recognizing natural scene categories[C]∥IEEE Conference on Computer Vision and Pattern Recognition(CVPR), New York, USA, 2006: 2169-2178. [本文引用:1]
[5]	Wu Lei, Hu Yang, Li Ming-jing, et al. Scale-invariant visual language modeling for object categorization[J]. IEEE Transactions on Multimedia, 2009, 11(2): 286-294. [本文引用:1]
[6]	Jiang Y, Wang R, Wang C. Scene classification with context pyramid features[J]. Journal of Computer-Aided Design and Computer Graphics, 2010, 22(8): 1366-1373. [本文引用:1]
[7]	纪昌明, 周婷, 向腾飞, 等. 基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用[J]. 电气自动化设备, 2014, 34(3): 125-127. Ji Chang-ming, Zhou Ting, Xiang Teng-fei, et al. Application of support vector machine based on grid search and cross validation in implicit stochastic dispatch of cascaded hydropower stations[J]. Electric Power Automation Equipment, 2014, 34(3): 125-127. [本文引用:1]
[8]	闫永刚, 马廷淮, 王建. KNN分类算法的MapReduce并行化实现[J]. 南京航空航天大学学报, 2013, 45(4): 550-555. Yan Yong-gang, Ma Ting-huai, Wang Jian. Parallel implementing KNN classification algorithm using Mapreduce programing model[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2013, 45(4): 550-555. [本文引用:1]
[9]	严利鑫, 黄珍, 朱敦尧, 等. 基于马尔科夫毯和隐朴素贝叶斯的驾驶行为险态辨识[J]. 吉林大学学报: 工学版, 2016, 46(6): 1851-1857. Yan Li-xin, Huang Zhen, Zhu Dun-yao, et al. Driving risk status identification based on Markov blanket hidden Naive Bayes[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(6): 1851-1857. [本文引用:1]
[10]	王寅同, 王建东, 陈海燕. 时间序列降维及机场噪声中的机型识别[J]. 吉林大学学报: 工学版, 2016, 46(4): 1202-1208. Wang Yan-tong, Wang Jian-dong, Chen Hai-yan. Time series dimensionality reduction and aircraft model recognition in airport-noise[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(4): 1202-1208. [本文引用:1]
[11]	汤鹏杰, 王瀚漓, 左凌轩. 并行交叉的深度卷积神经网络模型[J]. 中国图像图形学报, 2016, 21(3): 339-347. Tang Peng-jie, Wang Han-li, Zuo Ling-xuan. Parallel cross deep convolution neural networks model[J]. Journal of Image and Graphics, 2016, 21(3): 339-347. [本文引用:1]

2005

0.0

... 词袋模型(Bag-of-words,BOW)^[1]作为一种信息检索算法,在文本分类领域有着广泛的应用 ...

2013

0.0

. 2013, 34(5):1107-1112 DOI:doi:10.3969/j.issn.0254-3087.2013.05.022

Image matching based on improved sift algorithm

基于改进SIFT算法的图像匹配

Liu Jia , Fu Wei-ping , Wang Wen

刘佳, 傅卫平, 王雯

为进一步提高SIFT匹配算法的鲁棒性和正确率,从以下几个方面改进SIFT算法。对图像进行多分辨率小波变换,重建图像近似成分——低频信息参与匹配;采用"回"字形双层方邻窗将特征点邻域区域划分成四部分,建立32维特征点描述符向量;运用欧式距离初步确定匹配点,再用积分图像进一步剔除由于特征点具有空间相似性而出现的误匹配点,从而提高匹配精度。实验表明,本文算法在匹配精度和匹配时间上有明显提高,特别是当图像具有较多局部相似特征时,匹配点数增加,匹配正确率提高。

... 具体的做法为:先提取图像的SIFT^[2,3](Scale-invariant feature transform)特征,之后把视觉特征转换为一系列的图像视觉单词,最后,根据每一个视觉单词在图像中出现的概率来绘制直方图 ...

2015

0.0

. 2015, :-

The improvement of bag-of-visual-words model and its application research in images classification

视觉词袋模型的改进及其在图像分类中的应用研究

Sheng Hai-di

生海迪

近年来，随着互联网中数字图像不断激增，如何在海量图像中迅速准确地进行分类显然已经成为亟需解决的问题之一。现有的许多图像分类方法一般是通过提取图像底层特征来获得图像视觉信息，但因图像之间存在差别，所以不同图像提取的底层特征数目一般不同。为提高不同图像间的比较性能，研究者们将应用在文本分类领域的词袋模型应用到图像分类领域，称为视觉词袋模型。视觉词袋模型首先对图像进行底层特征提取与描述，对提取出的特征进行量化得到视觉词典，随后将每幅图像表示成基于相同维数的视觉单词频率直方图向量，将该向量作为对图像的描述，最后将图像描述向量代入到分类器中进行分类。本文围绕视觉词袋模型，针对图像分类的问题，对视觉词袋模型的特征提取方法、词典生成方法以及图像表示方法等进行研究，具体研究成果如下： (1)为避免常规构建视觉词袋模型在选取梯度方向离散精度时存在的盲目性，以及不恰当的离散精度构造出的视觉词袋模型分类率不高的问题，研究了在视觉词袋模型中提取图像特征时梯度方向离散精度是否存在明显的阈值，使得选取该阈值时能构造出最佳的视觉词袋模型。基于面向稠密特征提取图像局部特征描述，选择不同的梯度方向离散精度分别进行大量的实验，实验结果充分表明存在一个明显、统一的阈值24，选择该阈值构造的视觉词袋模型能够得到最高的正确分类结果。 (2)针对视觉词袋模型采用SIFT算法提取的特征点在区分度和代表性上不高的缺点，提出了一种基于Harris角点和dense SIFT特征加权的视觉词袋模型图像分类方法。采用快速密集网格划分对整幅图像提取dense SIFT特征，为获取特征更明显、更具有代表性的点，利用Harris角点检测算法对图像角点进行检测，以角点像素为中心提取该角点SIFT特征，并依据角点度为角点SIFT特征设置一定的权重，使角点SIFT特征相较于dense SIFT特征更加突出，以便更好地对图像进行描述。实验表明，该特征描述方法构造的视觉词袋模型能获得较高的分类正确率。 (3)针对空间金字塔视觉词袋模型缺少对局部特征之间语义分布关系的表达，提出了一种基于语义短语的空间金字塔视觉词袋模型图像表示方法。首先，将局部特征映射为具有一定语义信息的视觉单词，通过统计局部特征邻域范围内其他相关特征点的语义分布情况来构造语义短语。其次，将语义短语采用稀疏编码进行量化生成语义词典，图像则表示成基于语义词典的空间金字塔式稀疏统计直方图向量。最后，将图像表示向量代入分类器中进行训练和测试。实验结果表明，该视觉词袋模型构造方法能够较大幅度地提高图像分类的准确率。

2006

0.0

... Lazebnik等^[4]利用金字塔匹配核函数,提出了SPM模型(Spatial pyramid matching) ...

2009

0.0

... Wu等^[5]提出了视觉语言模型(Visual language model,VLM) ...

2010

0.0

... Jiang等^[6]利用随机划分图像来提高分类性能 ...

2014

0.0

. 2014, 34(3):125-127 DOI:doi:10.3969/j.issn.1006-6047.2014.03.021

Application of support vector machine based on grid search and cross validation in implicit stochastic dispatch of cascaded hydropower stations

基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用

Ji Chang-ming , Zhou Ting , Xiang Teng-fei

纪昌明, 周婷, 向腾飞

The combination of SVM（Support Vector Machine） theory combined with grid search and cross validation is applied to the implicit stochastic optimal dispatch of cascaded hydropower stations under the condition of uncertain inflow. With the minimum system structure risk taken as the training objective of SVM and the parameter distribution law combined，the exponentially divided grid is searched for determining the optimal model parameters. K-fold cross validation technique is adopted in the evaluation of SVM training performance，which decreases the influence of training sample randomness on the performance of training model and improves its generalization ability. The implicit stochastic optimal dispatch of cascaded hydropower stations is simulated on the hybrid programming platform of VC_ and MATLAB，which shows that，the implicit stochastic optimal dispatch based on SVM with optimized parameters enhances both power generation capacity and process.

将支持向量机（SVM）理论与网格搜索及交叉验证相结合，应用于梯级水电系统隐随机优化调度中，实现径流不确定条件下的梯级实际优化运行。以系统结构风险最小为SVM训练目标，结合参数分布规律，采用指数划分的网格搜索对模型参数进行优选；将K-fold交叉验证技术引入到SVM训练性能评价中，降低了训练样本随机性对训练模型性能的干扰，提高了模型的泛化能力。建立VC_与MATLAB混合编程平台，对梯级水电系统隐随机优化调度运行进行仿真，结果表明基于采用最优参数SVM的隐随机优化调度在梯级系统发电量和发电过程方面取得了良好成果。

... 本文使用支持向量机(Support vector machine,SVM)^[7]和K最近邻分类器(K-nearest neighbor,KNN)^[8]对图像进行分类,分别提出两种不同的分类方法 ...

2013

0.0

. 2013, 45(4):550-555 DOI:doi:10.3969/j.issn.1005-2615.2013.04.019

Parallel implementing KNN classification algorithm using Mapreduce programing model

KNN分类算法的MapReduce并行化实现

Yan Yong-gang , Ma Ting-huai , Wang Jian

闫永刚, 马廷淮, 王建

为了提高k-nearest neighbor algorithm(KNN)算法处理大数据集的能力,本文利用MapReduce并行编程模型,同时结合KNN算法自身的特点,给出了KNN算法在Hadoop平台下的并行化实现.通过设计Map、Combine和Reduce 3个函数,实现了KNN算法的并行化.Map函数完成每个测试样本与训练样本之间的相似度计算,Combine函数作为一个本地的Reduce操作,用以减少中间计算量及通信开销,Reduce函数则根据上述函数得到的中间结果计算出k近邻并作出分类判断.实验结果表明:较之以往的单机版方法,在Hadoop集群上实现的并行化KNN算法具有较好的加速比和良好的扩展性.

... 本文使用支持向量机(Support vector machine,SVM)^[7]和K最近邻分类器(K-nearest neighbor,KNN)^[8]对图像进行分类,分别提出两种不同的分类方法 ...

2016

0.0

. 2016, 46(6):1851-1857 DOI:doi:10.13229/j.cnki.jdxbgxb201606013

Driving risk status identification based on Markov blanket hidden Naive Bayes

基于马尔科夫毯和隐朴素贝叶斯的驾驶行为险态辨识

Yan Li-xin , Huang Zhen , Zhu Dun-yao

严利鑫, 黄珍, 朱敦尧

为了实现对驾驶行为险态的有效辨识,以实时采集的多源信息为依据,通过融合驾驶人心率变化率及违法行为将驾驶行为险态分为4级。采用马尔科夫毯特征抽取算法提取出速度、纵向加速度、前轮转角变化率、车道偏离量以及车辆位置作为构建驾驶行为险态辨识的特征集,基于隐朴素贝叶斯(HNB)构建驾驶行为险态辨识模型。十折交叉验证结果表明,该模型的辨识精度(90.6%)比朴素贝叶斯(NB)、贝叶斯网络(BN)及径向基函数(RBF)神经网络分别提高14.1%、13.9%和13%。此外,ROC曲线验证结果表明该模型对不同险态等级都具有良好的预测效果。

... 本文利用交叉验证法(cross-validate)^[9,10]选取最佳 K值 ...

2016

0.0

. 2016, 46(4):1202-1208 DOI:doi:10.13229/j.cnki.jdxbgxb201604028

Time series dimensionality reduction and aircraft model recognition in airport-noise

时间序列降维及机场噪声中的机型识别

Wang Yan-tong , Wang Jian-dong , Chen Hai-yan

王寅同, 王建东, 陈海燕

摘　要：为了提高非完整标记的高维机场噪声数据的处理速度和效率,研究了时间序列降维及机场噪声中的机型识别问题。首先采用概率类和不相关判别的半监督局部Fisher方法（SLFisher）得到降维转换矩阵,再将时间序列数据由高维空间映射到低维空间,最后在低维数据上进行k最近邻分类（kNN）。在国内某机场的实测噪声数据上的实验结果表明,SLFisher降维后机场噪声事件数据的机型识别效果取得显著提升。

... 本文利用交叉验证法(cross-validate)^[9,10]选取最佳 K值 ...

2016

0.0

. 2016, 21(3):339-347

Parallel cross deep convolution neural networks model

并行交叉的深度卷积神经网络模型

Tang Peng-jie , Wang Han-li , Zuo Ling-xuan

汤鹏杰, 王瀚漓, 左凌轩

... 4 实验及结果讨论本次实验在Caltech 101数据集和Caltech 256数据集中^[11]分别选取8个类别,并将数据集分为测试图像和训练图像两部分 ...