适用于单快拍的多重信号分类改进算法

引用本文

陈涛, 崔岳寒, 郭立民. 适用于单快拍的多重信号分类改进算法[J].吉林大学学报（工学版）, 2018,48(3): 952-956
CHEN Tao, CUI Yue-han, GUO Li-min. Improved algorithm of multiple signal classification for single snapshot[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 952-956 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170204
Permissions

适用于单快拍的多重信号分类改进算法

陈涛, 崔岳寒, 郭立民

哈尔滨工程大学信息与通信工程学院,哈尔滨 150001

通讯作者：郭立民(1977-),男,副教授,博士.研究方向:宽带信号检测、处理与识别.E-mail:guolimin@hrbeu.edu.cn

作者简介:陈涛(1974-),男,教授,博士.研究方向:宽带信号检测、处理与识别.E-mail:chentao@hrbeu.edu.cn

基金:国家自然科学基金项目(61571146); 中央高校基本科研业务费专项资金项目(HEUCFP201769).

摘要

经典多重信号分类(MUSIC)算法的子空间估计以多快拍数据估计得到的协方差矩阵为基础,在实际应用中,可用的快拍数并不确定。针对这一问题,本文提出了一种适用于单快拍的MUSIC改进算法,即ISS-MUSIC算法。该算法对经典MUSIC测向方法进行了改进,将伪协方差矩阵构造法与共轭增强法相结合。新算法的优点为适用于单快拍,且性能优于未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法。

关键词: 信息处理技术; 阵列信号处理; 波达方向估计; 单快拍; 经典多重信号分类算法

中图分类号:TN971.1 文献标志码:A 文章编号:1671-5497(2018)03-0952-05

Improved algorithm of multiple signal classification for single snapshot

CHEN Tao, CUI Yue-han, GUO Li-min

College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001,China

Abstract

The classical MUSIC algorithm based on the subspace estimation is dependent on covariance matrix estimation, which is built from a lot of snapshots. However, the number of the available snapshots is indeterminacy in the practical application. In order to solve the problem, we propose an improved MUSIC algorithm for single snapshot, called ISS-MUSIC algorithm. This algorithm improves the performance of the classical MUSIC algorithm, and it combines the method of constructing pseudo-covariance and the method of conjugate enhancement. The advantage of ISS-MUSIC algorithm is that it can be used in the case of single snapshot. Meanwhile, its performance outperforms the method of single snapshot MUSIC algorithm based on pseudo-covariance without enhancing conjugate.

Keyword: information processing technology; array signal processing; direction of arrival(DOA) estimation; single snapshot; classical multiple signal classification (MUSIC) algorithm

文章图片

0 引言

阵列信号处理是信号处理的一个重要分支, 着重于空间传输波携带信号的获取、处理和传输, 即对空间分布的组传感器接收的空间传输波信号进行处理以提取信息。

波达方向(Direction of arrival, DOA)估计作为阵列信号处理中的关键问题, 主要研究如何从背景噪声中估计信号的到达角信息^[1]。这个领域的研究经历了几十年的发展, 已经形成了比较系统的理论体系^[2]。DOA估计技术在雷达、声呐、地质开发、微波无线电通讯、生物医学等领域均有广泛的应用, 并取得了很大发展^[3]。由于子空间算法, 如MUSIC(Multiple signal classification)等可以突破瑞利极限, 实现超分辨, 所以近年来涌现出很多新型的基于子空间的测向算法^{[4, 5]}。

短快拍测向算法的研究主要针对军事和卫星通信, 在阵列接收数据有限、目标高速运动的前提下, 可以实现对目标的实时处理, 并具有较高的DOA估计精度, 可为高速运动目标的定位和跟踪提供技术支持^{[6, 7]}。单快拍类测向算法因其快拍数达到了短快拍的极限, 属于短快拍测向算法中的特殊情况, 而被单独归为一类进行研究, 近年来很多专家学者将研究的目光锁向少快拍甚至单快拍下的阵列信号处理^{[8, 9]}。

DOA估计算法以高分辨MUSIC算法和ESPRIT算法为代表^[10]。MUSIC算法中, 通常先得到协方差矩阵, 对其进行特征分解和奇异值分解后得到噪声子空间, 然后利用导向矢量与噪声子空间的正交性对信号入射方向进行估计^[1]。基于协方差矩阵MUSIC算法的渐近性能接近克拉美-罗界^{[11, 12]}, 但无法有效地应用于单快拍情况^{[13, 14]}。

本文分析了经典MUSIC算法不适用于单快拍的原因, 并对其进行了改进, 提出了一种适用于单快拍的MUSIC改进(Improved-single-snapshot MUSIC, ISS-MUSIC)算法。该方法将伪协方差矩阵构造法与共轭增强法相结合, 适用于单快拍, 且性能优于未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法。

1 信号模型

假设 $K$ 个同频不相关远场窄带信号入射到由 $M$ 个全向阵元组成的均匀线阵上, 信号数 $K$ 已知或已经估计得到, 于是阵列输出矢量为^[1]:

$x (t) = [x_{1} (t), x_{2} (t), \dots, x_{M} {(t)]}^{T} = As (t) + n (t) (1)$

式中:信号矢量 $s (t) = [s_{1} (t), s_{2} (t), \dots, s_{k} {(t)]}^{T};$ 噪声矢量 $n (t) = [n_{1} (t), n_{2} (t), \dots, n_{M} {(t)]}^{T};$ 导向矢量 $A = [a (θ_{1}), a (θ_{2}), \dots, a (θ_{k})], a (θ_{i}) = [1, e^{- j φ_{1}}, \dots, e^{- j (M - 1) φ_{i}}]^{T}, φ_{i} = 2 π d \sin (θ_{i}) / λ, θ_{i} 为第 i$ 个信号的入射角度, $λ$ 为信号波长。

假设入射信号为不相关的零均值平稳随机过程, 第 $i 个信号 s_{i} (t) (i = 1, 2, \dots, K)$ 的功率为 $σ_{s, i}^{2},$ 噪声为高斯白噪声, 每个阵元上的噪声功率为 $σ_{n}^{2},$ 信号与噪声不相关^[11]。

2 适用于单快拍的ISS-MUSIC算法

2.1 经典MUSIC算法不适用于单快拍的原因

在第1节的基础之上, 得到阵列输出数据的协方差矩阵为:

$R = E \{x (t) x^{H} (t)\} = AP A^{H} + s_{N}^{2} I (2)$

式中: $P$ 为信号协方差矩阵; $σ_{N}^{2} I$ 为噪声协方差矩阵; $I$ 为单位矩阵。

对 $R$ 进行特征分解, 有:

$R = \overset{M}{\sum_{i = 1}} α_{i} u_{i} {u^{H}}_{i} = SΛ S^{H} + s_{n}^{2} G G^{H} (3)$

式中: $S = [u_{1}, u_{2}, \dots, u_{k}]$ 为信号子空间; $G = [u_{k + 1}, u_{k + 2}, \dots, u_{M}]$ 为噪声子空间; $Λ = diag {α_{1}, α_{2}, \dots, α_{k}}$ 为对角阵, 其元素按从大到小排列为: $α_{1} \geq α_{2} \geq \dots \geq α_{k} > α_{k + 1} = \dots = α_{M} = σ_{n}^{2} 。$

信号子空间和噪声子空间是正交的, 而信号波达方向上的阵列导向矢量在信号子空间内, 所以其与噪声子空间是正交的, 于是MUSIC算法通过搜索下列的极大值点来估计信号DOA^[15]:

$f (θ) = \frac{1}{a^{H} (θ) G G^{H} a (θ)} (4)$

实际应用中, 只能得到协方差矩阵 $R 的估计值 R'$ (称为采样协方差矩阵), 通常取:

$R' = \frac{1}{L} \overset{L}{\sum_{l = 1}} x (l) x^{H} (l) (5)$

式中: $L$ 为快拍数。

对 $R'$ 进行特征分解后可得噪声子空间的估计值 $G',$ 此时搜索下列的极大值点来估计信号DOA:

$f' (θ) = \frac{1}{a^{H} (θ) G'G'^{H} a (θ)} (6)$

如果只有一个快拍可用, 由式(5)可知, 采样协方差矩阵的秩为1, 而信号子空间的秩是大于信号数的, 此时利用 $R'$ 的特征分解无法区分出信号子空间和噪声子空间, 因此经典MUSIC算法不适用于单快拍^[16]。

2.2 伪协方差矩阵构造方法

构造伪协方差矩阵的基本思想为:利用单快拍阵列接收信号, 构造伪协方差矩阵, 该矩阵可表示为: $Y = \bar{A} (θ) D {\bar{A}}^{T} (θ)$ 的形式。进而可利用常规的空间谱估计算法来实现DOA估计。其中 $D 为 K \times K$ 维的满秩矩阵; $\bar{A} (θ) = [\bar{a} (θ_{1}) \bar{a} (θ_{2}) \dots \bar{a} (θ_{k})]$ 为满足均匀线阵阵列流型的 $L \times K$ 维矩阵, 其中 $L$ 小于 $M 。 \bar{a} (θ_{k})$ 的第 $p$ 个元素可表示为: $\exp {j [φ_{k} + (p - 1) Δ φ_{k}]},$ 其中 $Δ φ_{k} = (2 π / λ) \sin θ_{k} 。$ 为保证伪协方差矩阵的秩为 $K,$ 应有 $L > K$ , 这样构造出来的伪协方差矩阵 $Y$ 是 $L \times L$ 维的。

矩阵 $Y 的元素 Y (p, q)$ 可表示为:

$\begin{array}{l} Y (p, q) = \overset{K}{\sum_{n = 1}} \overset{K}{\sum_{ω = 1}} \exp \{j [φ_{n} + (p - 1) Δ φ_{n}]\} \cdot \\ \exp \{- j [φ_{ω} + (q - 1) Δ φ_{ω}]\} d_{nω} (7) \end{array}$

式中: $d_{nw}$ 为矩阵 $D$ 的元素。

其中, 矩阵中的可利用信息可表示为如下形式:

${\bar{X}}_{m} = \overset{K}{\sum_{n = 1}} \exp \{j [φ_{n} + (m - 1) Δ φ_{n}]\} s_{n} (8)$

如果利用式(8)来构造式(7), 则 $Y (p, q)$ 可写成 ${\bar{X}}_{m} {\bar{X}}^{T}_{m}$ 的形式。

当矩阵 $D$ 为对角阵时, 式(7)可表示为:

$Y (p, q) = \overset{K}{\sum_{n = 1}} \exp \{j [φ_{n} + (p - q) Δ φ_{n}]\} d_{nn} (9)$

此时, 只要对角线元素不为0, 矩阵 $D$ 就是满秩的, 这样构造出来的伪协方差矩阵 $Y$ 可以表示成 $Y = \bar{A} (θ) D {\bar{A}}^{T} (θ)$ 的形式。由上述介绍可知, 伪协方差矩阵的构造方法是利用式(9)确定最终形式的矩阵。

由式(8)可知, $M$ 个阵列接收信号的相位是位于 $[φ_{n}, φ_{n} + (M - 1) Δ φ_{n}]$ 范围内的等差数列, 可表示的相位范围为 $(M - 1) Δ φ_{n},$ 固定相位 $φ_{n}$ 的取值与相位参考点的选择有关。这就是构造伪协方差矩阵时可用的信息。

假设 $s_{n} = s_{n}^{*},$ 则有:

${\bar{X}}_{m}^{*} = \overset{K}{\sum_{n = 1}} \exp \{- j [φ_{n} + (m - 1) Δ φ_{n}]\} s_{n} (10)$

式(10)的相位是位于 $[- φ_{n}, - φ_{n} - (M - 1) Δ φ_{n}]$ 范围内的等差数列, 这相当于增加了可利用的信息量。

基于以上理论, 令 $L = M 、 φ_{n} = 0 、 d_{nn} = s_{n}$ 并代入式(9), 此时伪协方差矩阵可表示为^[17]:

$Y = [\begin{array}{l} x_{1} & x_{2}^{*} & \dots & x_{M}^{*} \\ x_{2} & x_{1} & \dots & x_{M - 1}^{*} \\ ︙ & ︙ & ︙ \\ x_{M} & x_{M - 1} & \dots & x_{1} \end{array}] (11)$

2.3 共轭增强法

为进一步提高算法性能, 充分利用阵列输出数据的共轭信息, 在式(11)的基础上, 构造以下伪协方差矩阵^[18]:

$Y' = [Y, J Y^{*} J] (12)$

式中: $J$ 为交换矩阵, 其反对角线元素为1, 其他元素为0。

由式(12)可知, 此方法将 $M \times M$ 维伪协方差矩阵拓展为 $M \times 2 M$ 维

对拓展的伪协方差矩阵进行二阶积累, 公式如下^[16]:

$\begin{array}{l} R'_{yy} = \frac{1}{L} \overset{L}{\sum_{l = 1}} Y' (l) Y'^{H} (l) = \\ \frac{1}{L} \overset{L}{\sum_{l = 1}} [Y (l) Y'^{H} (l) + J Y^{*} (l) Y^{T} (l) J] = \\ R_{yy} + J R_{yy}^{*} J (13) \end{array}$

2.4 ISS-MUSIC算法的步骤

综上所述, 将2.2节与2.3节提出的方法进行合并为ISS-MUSIC算法, 其步骤如下:

步骤1 利用式(11)得到伪协方差矩阵 $Y 。$

步骤2 利用式(12)得到共轭增强后的伪协方差矩阵 $Y' 。$

步骤3 求伪协方差矩阵的二阶积累:

$R'_{yy} = \frac{1}{L} \overset{L}{\sum_{l = 1}} Y' (l) Y'^{H} (l)$

步骤4 对 $R'_{yy}$ 进行特征分解, 以得到噪声子空间 $U_{y 2}$ 。

步骤5 搜索谱函数:

$f_{ax} (θ) = \frac{1}{{\bar{a}}^{H} (θ) U_{y 2} {U_{y 2}}^{H} \bar{a} (θ)}$

的极大值点确定信号入射方向。

3 仿真试验及性能分析

3.1 ISS-MUSIC算法分辨能力

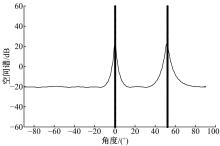
仿真条件:均匀线阵的阵元数为8; 阵元间距为半波长; 快拍数为1; 信噪比为10 dB; 入射角分别在0° ~10° 和50° ~60° 随机产生。ISS-MUSIC算法的空间谱图如图1所示, 图中的两条竖线为原入射角度。由图1可知, ISS-MUSIC算法具有较好的信号分辨能力。

	Figure Option View Download New Window
	图1 ISS-MUSIC的空间谱图Fig.1 Space spectrum of ISS-MUSIC

3.2 测角精度比较

将ISS-MUSIC算法与未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法进行性能比较。仿真中, 均匀线阵的阵元数为8; 阵元间距为半波长; 快拍数为1; 入射角在0° ~90° 随机产生。两种算法随信噪比变化的测向精度如图2所示。

	Figure Option View Download New Window
	图2 测向精度Fig.2 Accuracy of DOA

由图2可知, ISS-MUSIC算法的测向精度高于未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法的测向精度。

4 结束语

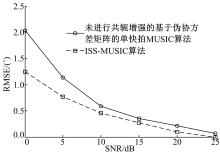
提出了一种单快拍下的测向算法。该算法对经典MUSIC测向算法进行了改进, 将伪协方差矩阵构造法与共轭增强法相结合。仿真试验结果表明:ISS-MUSIC算法在单快拍的条件下有较好的信号分辨能力, 且测向精度优于未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2005. [本文引用:3]
[2]	Zeng Hao, Ahmad Z, Zhou Jian-wen. DOA estimation algorithm based on adaptive filtering in spatial domain[J]. China Communication, 2016, 12(13): 49-58. [本文引用:1]
[3]	李新波, 石要武, 马彦, 等. 基于RARE-cumulant的互耦矫正和DOA估计[J]. 吉林大学学报: 工学版, 2010, 40(4): 1118-1121. Li Xin-bo, Shi Yao-wu, Ma Yan, et al. Mutual coupling calibration and direction of arrival estimation based on RARE-cumulant algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(4): 1118-1121. [本文引用:1]
[4]	Forster P, Ginolhac G, Boizard M. Derivation of the theoretical performance of a Tensor MUSIC algorithm[J]. Signal Processing, 2016, 129(1): 97-105. [本文引用:1]
[5]	Kintz A L, Gupta I J. A modified MUSIC algorithm for direction of arrival estimation in the presence of antenna array manifold mismatch[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(11): 4836-4847. [本文引用:1]
[6]	Tervo S. Single snapshot detection and estimation of reflections from room impulse responses in the spherical harmonic domain[J]. IEEE-ACM Transactions on Audio Speech and Language Processing, 2016, 24(12): 2466-2480. [本文引用:1]
[7]	Chen Chun-hui, Zhang Qun, Gu Fu-fei. 2D single snapshot imaging using MIMO radar based on SR[J]. Electronics Letters, 2016, 52(23): 1946-1948. [本文引用:1]
[8]	Elbir A M, Tuncer T. 2-D DOA and mutual coupling coefficient estimation for arbitrary array structures with single and multiple snapshots[J]. Dignal Signal Processing, 2016, 54: 75-86. [本文引用:1]
[9]	王凌, 李国林. 利用单次快拍实现相干信源二维测向的新算法[J]. 北京理工大学学报, 2015, 35(5): 512-518. Li Ling, Li Guo-lin. A new algorithm of 2D DOA whose source is coherent with single snapshot[J]. Journal of Beijing Institute of Technology, 2015, 35(5): 512-518. [本文引用:1]
[10]	李新波, 李晓青, 刘国君, 等. 用于声矢量阵列波达方向估计的四元数最小范数法[J]. 光学精密工程, 2014, 22(7): 1969-1975. Li Xin-bo, Li Xiao-qing, Liu Guo-jun, et al. Quaternion min-norm algorithm for DOA estimation with acoustic vector sensor array[J]. Optics and Precision on Engineering, 2014, 22(7): 1969-1975. [本文引用:1]
[11]	Stoica P, Nehorai A. MUSIC maximum likelihood, and Cramer-Rao bound[J]. IEEE Transactions on Acoustics, Speech, and Signal Process, 1989, 37(5): 720-741. [本文引用:2]
[12]	Suryapakash R T, Nadakuditi R R. Consistency and MSE performance of MUSIC-based DOA of a single source in white noise with rand omly missing data[J]. IEEE Transactions on Signal Processing, 2015, 63(18): 4756-4770. [本文引用:1]
[13]	Liao W, Fannjiang A. MUSIC for single-snapshot spectral estimation: stability and super-resolution[J]. Applied and Computational Harmonic Analysis, 2016, 40(1): 33-67. [本文引用:1]
[14]	Hacker P, Yang B. Single snapshot DOA estimation[J]. Advances in Radio Science, 2010, 8(1921): 251-256. [本文引用:1]
[15]	Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984-995. [本文引用:1]
[16]	刘剑, 宋爱民, 余侃民, 等. 适用于任意快拍数的MUSIC算法[C]∥2016全国电子战学术交流大会. 北京: 中国电子学会, 2016: 562-567. [本文引用:2]
[17]	谢鑫, 李国林, 刘华文. 采用单次快拍数据实现相干信号DOA 估计[J]. 电子与信息学报, 2010, 32(3): 604-608. Xie Xin, Li Guo-lin, Liu Hua-wen. DOA estimation of coherent signals using one snapshots[J]. Journal of Electronics & Information Technology, 2010, 32(3): 604-608. [本文引用:1]
[18]	Wen Zhong, Li Li-ping, Wei Ping. Fast direction finding using modified pseudocovariance matrix[J]. IEEE Transactions on Antennas Propagat, 2006, 54(12): 3914-3918. [本文引用:1]

2005

0.0

... 波达方向(Direction of arrival,DOA)估计作为阵列信号处理中的关键问题,主要研究如何从背景噪声中估计信号的到达角信息^[1] ...

... MUSIC算法中,通常先得到协方差矩阵,对其进行特征分解和奇异值分解后得到噪声子空间,然后利用导向矢量与噪声子空间的正交性对信号入射方向进行估计^[1] ...

... 1 信号模型假设 K个同频不相关远场窄带信号入射到由 M个全向阵元组成的均匀线阵上,信号数 K已知或已经估计得到,于是阵列输出矢量为^[1]: ...

2016

0.0

... 这个领域的研究经历了几十年的发展,已经形成了比较系统的理论体系^[2] ...

2010

0.0

. 2010, 40(4):1118-1121

Mutual coupling calibration and direction of arrival estimation based on RARE-cumulant algorithm

基于RARE-cumulant的互耦矫正和DOA估计

Li Xin-bo , Shi Yao-wu , Ma Yan

李新波, 石要武, 马彦

Based on fourth-order cumulant and the special mutual coupling transform model of uniform and linear arrays, a novel efficient mutual coupling compensation algorithm for estimation of Direction of Arrival (DOA) is proposed. This is an online calibration method and the calibration sources are not required. Although the fourth-order cumulant is more complex than traditional second-order method, it can obtain more spatial information and the number of mutual coupling coefficients is not expanded with the increase in virtual arrays. In the case of Gaussian color noise, simulation results demonstrate the effectiveness of the proposed technique. The results also show that the estimation resolution of the algorithm is higher than that of both the second-order mutual coupling calibration method and the traditional fourth-order method without mutual coupling consideration.

基于四阶累计量及RARE (RAnk reduce equation)变换，结合均匀线阵互耦矩阵的特殊性，提出了一种新的互耦校正及波达方向估计算法。虽然四阶累计量比传统的二阶方法算法复杂，却扩展了阵列孔径，提高了在色噪声背景下DOA估计精度，而互耦系数并未因增加了虚拟阵元而增多。RARE变换将互耦系数与波达方向参量分离，有效地实现了多维参数估计的降维处理，减小了多维参量估计的计算量。仿真实验表明，在高斯色噪声背景下，本文方法计算量小，而且估计能力明显优于二阶去耦算法和传统的四阶方法。

... DOA估计技术在雷达、声呐、地质开发、微波无线电通讯、生物医学等领域均有广泛的应用,并取得了很大发展^[3] ...

2016

0.0

... 由于子空间算法,如MUSIC(Multiple signal classification)等可以突破瑞利极限,实现超分辨,所以近年来涌现出很多新型的基于子空间的测向算法^[4,5] ...

2016

0.0

... 由于子空间算法,如MUSIC(Multiple signal classification)等可以突破瑞利极限,实现超分辨,所以近年来涌现出很多新型的基于子空间的测向算法^[4,5] ...

2016

0.0

... 短快拍测向算法的研究主要针对军事和卫星通信,在阵列接收数据有限、目标高速运动的前提下,可以实现对目标的实时处理,并具有较高的DOA估计精度,可为高速运动目标的定位和跟踪提供技术支持^[6,7] ...

2016

0.0

2016

0.0

... 单快拍类测向算法因其快拍数达到了短快拍的极限,属于短快拍测向算法中的特殊情况,而被单独归为一类进行研究,近年来很多专家学者将研究的目光锁向少快拍甚至单快拍下的阵列信号处理^[8,9] ...

2015

0.0

. 2015, 35(5):512-518 DOI:doi:10.15918/j.tbit1001-0645.2015.05.015

A new algorithm of 2D DOA whose source is coherent with single snapshot

利用单次快拍实现相干信源二维测向的新算法

Li Ling , Li Guo-lin

王凌, 李国林

In order to estimate two-dimensional direction-of-arrival(DOA) of coherent signal sources fast in complex electromagnetic interference environment, the paper reconstructs three data matrixes which use the observed data vector directly and can realize decorrelation in three different dimensions according to the characteristic of three orthogonal linear arrays. Combined with ESPRIT algorithm, the 2-D DOA can be estimated fast. Using one single snapshot, the proposed algorithm doesn't need to calculate covariance matrix. The problem of estimating 2-D DOA can be transformed to three 1-D DOA estimations which can be carried out synchronously, so the algorithm reduces calculation amount and this is helpful to project implementation. The proposed algorithm exists the problem of aperture loss and estimation error caused by one single snapshot. Using the characteristic of noncircular signals and the accumulation of the same phase data, the method can improve the degree of freedom of array and estimation performance. The simulation results show the effectiveness of the proposed algorithm and the countermeasures.

针对复杂电磁干扰背景下相干信源二维波达方向的快速估计问题,根据垂直阵列系统特点,利用单次快拍数据在3个不同维度构造了数据矩阵实现解相干,并结合ESPRIT算法实现了二维DOA的快速估计. 该算法仅利用单次快拍数据,不需要进行协方差矩阵的计算,并将二维DOA估计问题转化为3个一维DOA估计,可同时在3个维度并行处理,因此运算量大大降低,利于工程实现. 针对算法存在阵列孔径损失和仅采用一次快拍数据量导致的估计误差偏大问题,利用非圆信号特征和同相位数据叠加,改善了算法的估计性能,提高了阵列自由度. 数值仿真验证了本文算法及提高估计精度对策的有效性.

2014

0.0

. 2014, 22(7):1969-1975 DOI:doi:10.3788/OPE.20142207.1969

Quaternion min-norm algorithm for DOA estimation with acoustic vector sensor array

用于声矢量阵列波达方向估计的四元数最小范数法

Li Xin-bo , Li Xiao-qing , Liu Guo-jun

李新波, 李晓青, 刘国君

由于四元数MUSIC(Multiple Signal Classification)算法计算量较大,本文结合声矢量传感器的四元数导向矢量模型,提出了一种声矢量阵列波达方向估计的四元数最小范数法。首先,将声矢量阵列输出协方差矩阵奇异值分解所得到的(M-N)×M维(M为阵元数、N为信源数)噪声子空间依最小范数(Minimum-Norm,MN)准则构建为一个新的四元数域1×M维噪声矢量。接着,提出了简化的谱峰搜索公式,理论分析了四元数最小范数法在搜索计算量上的优势。对提出的算法与Q-MUSIC算法进行了对比。结果显示:该算法至少能节省50%的谱峰搜索量。同时,提出的算法构建的低维噪声矢量与导向矢量间的正交性优于高维噪声子空间与导向矢量间的正交性,在0dB时,其范德蒙范数和谱峰分别为Q-MUSIC算法的1/3和3倍。另外,该算法在减小谱峰搜索量的同时,可以较好地分辨信源波达方向,且其统计特性与四元数MUSIC算法相当。提出的算法不局限于L线阵,也适用于双平行线阵及面阵。

... DOA估计算法以高分辨MUSIC算法和ESPRIT算法为代表^[10] ...

1989

0.0

... 基于协方差矩阵MUSIC算法的渐近性能接近克拉美-罗界^[11,12],但无法有效地应用于单快拍情况^[13,14] ...

... 假设入射信号为不相关的零均值平稳随机过程,第 i个信号si(t)(i=1,2,…,K)的功率为 σs,i2,噪声为高斯白噪声,每个阵元上的噪声功率为 σn2,信号与噪声不相关^[11] ...

2015

0.0

... 基于协方差矩阵MUSIC算法的渐近性能接近克拉美-罗界^[11,12],但无法有效地应用于单快拍情况^[13,14] ...

2016

0.0

... 基于协方差矩阵MUSIC算法的渐近性能接近克拉美-罗界^[11,12],但无法有效地应用于单快拍情况^[13,14] ...

2010

0.0

... 基于协方差矩阵MUSIC算法的渐近性能接近克拉美-罗界^[11,12],但无法有效地应用于单快拍情况^[13,14] ...

1989

0.0

... 信号子空间和噪声子空间是正交的,而信号波达方向上的阵列导向矢量在信号子空间内,所以其与噪声子空间是正交的,于是MUSIC算法通过搜索下列的极大值点来估计信号DOA^[15]: ...

2016

0.0

... 如果只有一个快拍可用,由式(5)可知,采样协方差矩阵的秩为1,而信号子空间的秩是大于信号数的,此时利用 R'的特征分解无法区分出信号子空间和噪声子空间,因此经典MUSIC算法不适用于单快拍^[16] ...

... 对拓展的伪协方差矩阵进行二阶积累,公式如下^[16]: ...

2010

0.0

. 2010, 32(3):604-608

DOA estimation of coherent signals using one snapshots

采用单次快拍数据实现相干信号DOA 估计

Xie Xin , Li Guo-lin , Liu Hua-wen

谢鑫, 李国林, 刘华文

... 基于以上理论,令 L=M、φn=0、dnn=sn并代入式(9),此时伪协方差矩阵可表示为^[17]: ...

2006

0.0

... 3 共轭增强法为进一步提高算法性能,充分利用阵列输出数据的共轭信息,在式(11)的基础上,构造以下伪协方差矩阵^[18]: ...