基于Hyb-F组合滤波算法的向海自然保护区NDVI时间序列重构

引用本文

刘舒, 姜琦刚, 朱航, 李晓东. 基于Hyb-F组合滤波算法的向海自然保护区NDVI时间序列重构[J].吉林大学学报（工学版）, 2018,48(3): 957-967
LIU Shu, JIANG Qi-gang, ZHU Hang, LI Xiao-dong. Reconstruction of Landsat NDVI time series of Xianghai natural deserve based on a hybrid filtering algorithm Hyb-F[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 957-967 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170865
Permissions

基于Hyb-F组合滤波算法的向海自然保护区NDVI时间序列重构

刘舒¹, 姜琦刚¹, 朱航², 李晓东^1,³

1.吉林大学地球探测科学与技术学院, 长春 130026

2.吉林大学机械科学与工程学院, 长春 130022

3.白城师范学院旅游与地理科学学院, 吉林白城137000

通讯作者：朱航(1982-),女,副教授,博士.研究方向:航空遥感及多源遥感信息融合技术.E-mail:hangzhu@jlu.edu.cn

作者简介:刘舒(1988-),女,博士研究生.研究方向:遥感地学和环境遥感.E-mail:liushu8877@126.com

基金:中国地质调查局项目(DD2016007706); 国土资源部公益性行业科研专项基金项目(201511078-1); 国家自然科学基金青年基金项目(31501218).

摘要

针对借助遥感手段直接获取的归一化植被指数(NDVI)时间序列含有噪声数据,而单一应用局部或全局时间序列重构算法不能完全剔除噪声,重构精度受到一定影响的问题,本文将局部Savitzky-Golay(S-G)滤波、全局非对称高斯(Asymmetric Gaussian, AG)拟合原理和格拉布斯(Grubbs)检验算法相结合,构建Hyb-F组合式滤波法,重构向海自然保护区8种覆被类型的Landsat NDVI时间序列。首先,通过设定指标阈值剔除序列部分无效值;其次,采用引入Grubbs检验的S-G算法,剔除局部异常值;再次,采用引入Grubbs检验的AG拟合算法,剔除全局异常值;最后,利用S-G滤波算法平滑曲线,得到最终拟合结果。研究表明,该算法对灌木林地、草地、乔木林地和旱田等有植被生长覆被类型样本的拟合结果与纯净数据间相关性较强,相关系数(CC)达0.8488~0.9215,均方根误差(RMSE)为0.0429~0.1057。对盐碱地、建设用地、水域等非植被生长类型的数据具有较好的平滑作用。该算法对整个研究区数据重建效率指数为0.59,可有效地模拟原始数据。相比于单一滤波算法,Hyb-F滤波法具有更强的噪声识别能力,降低噪声引起的峰值损失,不仅能更好地模拟植被生长规律,并且能保留曲线细部特征,获得较高拟合精度。

关键词: 遥感; 组合滤波算法; Savitzky-Golay滤波; 非对称高斯拟合; 格拉布斯检验; 归一化植被指数时间序列

中图分类号:TP79 文献标志码:A 文章编号:1671-5497(2018)03-0957-11

Reconstruction of Landsat NDVI time series of Xianghai natural deserve based on a hybrid filtering algorithm Hyb-F

LIU Shu¹, JIANG Qi-gang¹, ZHU Hang², LI Xiao-dong^1,³

1.College of Geo-exploration Science and Technology, Jilin University, Changchun 130026, China

2.College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

3.College of Tourist and Geoscience, Baicheng Normal College, Baicheng 137000, China

Abstract

Normalized Difference Vegetation Index (NDVI) time series exactly derived from remote sensing data are usually contaminated by different types of noise. Only by adopting the local or global filtering algorithm can not eliminate all kinds of noise from NDVI time series and maintain their local or global characters at the same time. A hybrid filtering algorithm, called Hyb-F, is proposed based on Savitzky-Golay filter, Asymmetric Gaussian algorithm and the Grubbs test method. Then, Hyb-F, which is a four step method, is used to reconstruct the Landsat NDVI time series for eight land cover types within Xianghai National Natural Reserve. First, the obvious outliers are detected and removed by setting thresholds for Normalized Difference Snow Index (NDSI), standard deviation and boundaries of NDVI. Second, via combing Grubbs test and Savitzky-Golay filter, the local outliers are removed. Third, via combing Grubbs test and Assymmetric Gaussian algorithm, the global outliers are removed. Finally, the final NDVI time series are built by using the Savitzky-Golay filter. The shape of fitting curves, statistical indicators and regional application effect of Hyb-F are analyzed. The results of the proposed Hyb-F method are compared with that of only Savitzky-Golay filter or Asymmetric Gaussian algorithm. For the land cover types with vegetation, Hyb-F performs well to the samples of shrub land, grassland, forest and cropland. Results of the mentioned types show large correlation with the clean reference series. The correlation coefficients are from 0.8488 to 0.9215 and the root mean square errors are from 0.0429 to 0.1057. The results of the first two land cover types achieve the highest accuracy among all the methods discussed. For the types without vegetation, such as saline, construction land and water area, the Hyb-F method can smooth the curves well. Compared with other methods, Fyb-F takes all local and global characters and dynamic trends into consideration. It can effectively recognize different types of outliers. Besides, it can weaken the loss of peak values and model the annual growing pattern of land cover types with vegetation. When applied to the whole study region, the indicator of efficiency of reconstruction is 0.59, demonstrating the reliability of Fyb-F. Moreover, the work flow the proposed method is clear and it is easy for application.

Keyword: remote sensing; hybrid filtering algorithm; Savitzky-Golay filter; asymmetric Gaussian; Grubbs test; NDVI time series

文章图片

0 引言

归一化植被指数(NDVI)时间序列是反映植被与地表气候条件、人类活动间响应关系的重要工具。然而由卫星直接获取的遥感数据得到的NDVI时间序列中存在来自云、冰雪、阴影、气溶胶双向反射等多种噪声, 在应用前应去除噪声, 重构时间序列^{[1, 2, 3]}。

常见NDVI序列重构方式有:基于局部数据的阈值法、最大值合成法(MVC)、Savitzky-Golay滤波法等; 基于全局或半全局数据的非对称高斯拟合法、双逻辑函数拟合法^{[4, 5]}和时间序列谐波分析法^{[6, 7]}等。不同重构方法对不同区域或不同数据源的适用性不同, 多位学者提出了各算法的对比结果, 但各算法优劣目前并无定论^[2]。

目前已有学者对一些单一类型数据重构算法进行改进^{[3, 8]}, 或同时利用两类滤波算法构建组合式滤波算法^{[2, 9, 10]}, 提高NDVI时间序列重构精度和重构过程的自动化程度, 但相关研究仍存在以下局限。首先, 局部滤波算法较好地保留序列细部特征, 但滤波结果不遵循植被生长规律, 而全局滤波算法所得结果符合植被生长规律, 但在局部存在过度平滑现象。其次, 两类算法所得结果都容易受噪声影响, 且对噪声过滤能力有限。为更形象地描述滤波效果, 将噪声分为两类, 一类是能被局部滤波算法识别的局部噪声, 另一类为能被全局滤波算法识别的不符合植被总体生长趋势的噪声, 称为全局噪声。最后, 在目前的组合滤波法中, 各组成部分仍相对独立, 去噪过程由局部滤波法完成, 而未能被局部算法识别的全局噪声则被保留, 继续参与NDVI序列重构。以上局限都在一定程度上影响重构序列的精度。

本文构建了一种新型组合滤波算法Hyb-F (Hybrid filtering method based on Grubbs-introduced S-G and AG algorithms), 将局部S-G滤波和全局AG拟合算法相结合, 并在各自过程中引入Grubbs检测算法。该组合算法优点在于分步剔除序列局部噪声和全局噪声, 构建具有精细细部特征, 同时反映植被物候变化的NDVI时间序列, 并以向海自然保护区为研究区, 分析组合算法的性能。

1 材料与方法

1.1 研究区地理概况

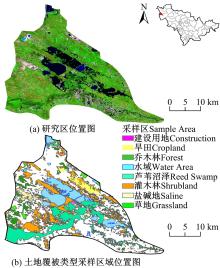
向海自然保护区位于吉林省通榆县西北部, 地理范围为122° 05'~122° 35'E, 44° 50'~45° 19'N(图1(a), 保护区范围由通榆县地图矢量化获得), 是吉林省唯一列入《国际重要湿地名册》的重要湿地。保护区内多种珍稀野生动植物繁育, 多样生态景观共存^[11]。向海自然保护区内的地表覆被类型如图1(b)所示, 主要是以蒙古黄榆、大果榆为主的灌木林地, 杨树为主的乔木林地, 以芦苇、香蒲为主的沼泽湿地, 以羊草为主的草地, 以玉米田为主的耕地, 大片水域, 出露的重度盐碱地和零星分布的城镇工矿建设用地^{[12, 13]}。

	Figure Option View Download New Window
	图1 向海自然保护区Fig.1 Xianghai natural reserve

1.2 数据来源

本研究选取Landsat8 陆地成像仪(OLI)获取的多光谱影像组成基础数据集。影像从USGS网站(https://glovis.usgs.gov/)下载, 为L1T级数据, 已经过系统辐射校正和精细几何校正, 空间分辨率为30 m, 时间分辨率为16天。覆盖研究区影像编号为120/029(带/行), 为尽量保证影像获取年份一致, 避免数据集中连续多期影像存在云雪“ 污染” , 最终选取2015年1月至2016年12月获取的数据构成影像序列集, 个别时段连续多期数据云覆盖度大, 由2014年相应时段数据补充。共选取27期影像, 基本信息如表1所示。

表1 Landsat8 OLI数据基本特征(行列号:120/029) Table 1 Main characters of Landsat8 OLI imagery (path/row:120/029)

将影像在ENVI5.1中进行大气校正, 将投影参数定义为WGS84椭球参数下的UTM投影(Zone51)。分别利用各期红光波段和短波红外波段计算相应影像的NDVI。其中, 由2015年5月13日数据得到的NDVI不参与拟合过程, 仅作为辅助数据, 验证数据序列重构实验效果。将数据按年内时间顺序组合成一幅具有26个波段的NDVI时间序列影像。

1.3 研究方法

1.3.1 设定指标阈值剔除噪声

直接算得的NDVI序列存在超出理论值域等与实际不符的无效点, 因此, 首先将移动窗口长度设为5, 通过设定曲线各点取值、变化量、变化量与变化方向的关系、雪盖指数等指标的阈值, 识别移动窗口中超出理论值的噪声和部分云、雪噪声。剔除窗口中噪声, 并以其他值的二次多项式最小二乘拟合曲线在噪声点的取值代替原始值。

1.3.2 Grubbs异常点检验

Grubbs检验是一种常见的离群异常值检验方法, 通过检验观测值残差的Grubbs统计量与某水平下的临界值之间的关系, 判断异常点位置。

本研究的噪声点在剔除过程中, 分别将Grubbs检验过程与S-G滤波算法和AG拟合算法相结合, 判断时间序列中存在的局部异常点和全局异常点。假定进行S-G滤波前后或AG拟合过程前后时间序列的差值序列为NDVI_C, Grubbs检验具体实现方法为:将NDVI_C由小到大排列, 并计算各点Grubbs统计量, 查表获得显著性水平 $α$ 下的上下临界值, 找出NDVI_C最大值和最小值点中Grubbs统计量较大的点, 判断该点Grubbs统计量与临界值的关系。若统计量超过临界值的范围, 则该点为异常点^[8]。将Grubbs检测的显著性水平选为0.05, 为防止对异常点的误判断, 本文通过迭代过程实现异常点剔除, 每次迭代仅剔除一个偏差最严重的点。在两步去噪过程中, 噪声点的去噪后取值分别为以该点为中心的S-G移动窗口内基于其他点的S-G滤波曲线在该点的取值, 或剔除该点后的AG拟合曲线在该点的取值。剔除一个异常点后, 得到新的待降噪NDVI序列, 并计算新的NDVI_C序列, 继续Grubbs检验, 直到将所有异常点剔除。

1.3.3 Savitzky-Golay滤波算法

Savitzky-Golay滤波算法(S-G)是一种基于最小二乘原理对滑动窗口内数据进行卷积运算的数据平滑方式。对于以第 $j$ 点为中心, 宽度为N的滑动窗口, S-G算法基本数学表达式为:

$p_{j} = \frac{1}{N} \overset{i = m}{\sum_{i = - m}} C_{i} q_{j + i} (1)$

式中:q_i为原始序列第i个数据取值; p_j为平滑后序列第j个数据取值; N为滑动窗口长度; m为窗口中间至一侧端点的长度, N=2m+1; C_i为第i个数据的系数。

当高质量数据在整个时间序列所占比例较高时, S-G算法能够过滤序列噪声, 较细致地描述序列局部特征^[14]。

在实际运算中, S-G滤波曲线由移动窗口内数据二次多项式的最小二乘拟合得出。由于时间序列中存在噪声污染的影像所占比例较大, 存在局部集中情况, 且无其他质量控制数据, 将研究中涉及的S-G滤波过程窗口长度设为7。

本研究中两次运用S-G滤波算法, 分别用于局部异常值的剔除与最终时序数据的重构。

1.3.4 非对称高斯拟合算法

非对称高斯拟合算法(Asymmetric Gussian, AG)是一种基于高斯函数拟合的非线性重构算法。该算法根据数据序列极值点所在位置将数据分段, 对每段数据分别进行高斯函数拟合, 并利用区间端点附近的平滑截断函数连接每段曲线, 实现全局拟合。整个拟合过程分以下2步完成:

首先, 将两个波峰或波谷间的数据划分为左、中、右3部分, 3个峰值点位置由 $t_{L} 、 t_{C}$ 和 $t_{R}$ 表示。利用局部高斯平滑函数分别拟合每一段曲线, 该函数的数学表达式为:

$\begin{array}{l} f (t) = f (t; b_{1}, b_{2}, a_{1}, a_{2}, \dots, a_{5}) = \\ b_{1} + b_{2} g (t; a_{1}, a_{2}, \dots, a_{5}) (2) \end{array}$

式中:高斯函数的具体形式为:

$\begin{array}{l} g (t; a_{1}, a_{2}, \dots, a_{5}) = \\ \{\begin{array}{l} \exp [- {(\frac{t - a_{1}}{a_{2}})}^{a_{3}}], t > a_{1} \\ \exp [- {(\frac{a_{1} - t}{a_{4}})}^{a_{5}}], t < a_{1} \end{array} (3) \end{array}$

参数 $b_{1}$ 和 $b_{2}$ 控制高斯函数g的基线位置和振动幅度, $a_{1}$ 控制局部拟合区域函数峰值的位置, $a_{2} 、 a_{3} 、 a_{4}$ 和 $a_{5}$ 分别决定局部拟合区域右、左部分函数的宽度和陡缓程度。

最后, 利用全局方程 $F (t)$ 衔接整个[ $t_{L}, t_{R}$ ]时段各局部函数。全局函数数学表达式为:

$\begin{array}{l} F (t) = \\ \{\begin{array}{l} α (t) f_{L} (t) + [1 - α (t)] f_{C} (t), t_{L} < t < t_{C} \\ β (t) f_{C} (t) + [1 - β (t)] f_{R} (t), t_{C} < t < t_{R} \end{array} (4) \end{array}$

式中: $f_{L} (t) 、 f_{C} (t)$ 和 $f_{R} (t)$ 分别为左、中、右3部分的局部高斯拟合函数; $α (t)$ 和 $β (t)$ 为由0到1平滑过渡的截断函数^{[4, 5]}。

在本研究中, 非对称高斯拟合主要与Grubbs检测算法相结合, 应用于全局噪声的剔除。

Hyb-F组合滤波算法具体流程如图2所示。

	Figure Option View Download New Window
	图2 时间序列滤波算法流程图Fig.2 Workflow of the hybrid filtering algorithm

1.3.5 NDVI时间序列重建效果评价方法

为评价Hyb-F组合滤波方式对NDVI时间序列的重建效果, 在图1(b)所示覆被区选择样本点, 提取各层NDVI取值, 利用Hyb-F算法重构样本NDVI时间序列, 并采用AG算法和S-G滤波算法进行对比实验。AG算法和S-G滤波算法的迭代过程对剔除低值噪声, 提高拟合精度起到较大作用。因此, 实际对比了Hyb-F滤波结果与原始序列(Original)、S-G直接滤波结果(S-G Direct)、S-G三次迭代滤波结果(S-G with 3 iterations)、AG直接滤波结果(AG Direct)和AG三次迭代滤波结果(AG with 3 iterations)。

本研究中, 对不同方法的数据重构效果分别采用视觉直观验证和样本点重构序列统计指标定量分析两种方式进行对比。

统计指标定量分析的基础在于构建准确的参考时间序列。由于实际条件限制, 观测量会有一定偏差, 研究者很难通过其获取真实的NDVI时间序列。本文对比实验定量评价基于以下假定:

若重构算法不能完全剔除原始序列中被云和雪污染的数据点, 则拟合过程不能成功滤除原有高质量数据中存在的微小偏差, 且拟合结果还可能降低原有高质量数据本身的精度。为此, 将原序列中的高质量数据与同时刻的重构NDVI数据提取出来分别作为参考子序列和重构子序列, 并计算两者间相关系数(Correlation coefficient, CC)、均方根误差(Root mean square error, RMSE)、平均绝对误差(Mean absolute error, MAE)、平均相对误差(Mean relative error, MRE)和效率系数(Coefficient of efficiency, CE), 来定量评价算法重构效果。评价指标计算公式如下:

$\begin{array}{l} CC = \frac{\overset{n}{\sum_{i = 1}} (p_{i} - \bar{p}) (q_{i} - \bar{q})}{\sqrt{\overset{n}{\sum_{i = 1}} {(p_{i} - \bar{p})}^{2}} \sqrt{\overset{n}{\sum_{i = 1}} {(q_{i} - \bar{q})}^{2}}} (5) \\ RMSE = \sqrt{\frac{\overset{n}{\sum_{i = 1}} (p_{i} - q_{i})^{2}}{n}} (6) \\ MAE = \frac{1}{n} \overset{n}{\sum_{i = 1}} |p_{i} - q_{i}| (7) \\ MRE = \frac{1}{n} \overset{n}{\sum_{i = 1}} \frac{|p_{i} - q_{i}|}{|q_{i}|} (8) \\ CE = 1 - \frac{\overset{n}{\sum_{i = 1}} (p_{i} - q_{i})^{2}}{\overset{n}{\sum_{i = 1}} (q_{i} {- \bar{q})}^{2}} (9) \end{array}$

式中: $p_{i}$ 为重构序列中第i个点的NDVI取值; $q_{i}$ 为原始数据中第i个点的NDVI取值; $\bar{q}$ 为原始序列中各点的NDVI平均值。指标CE的取值体现拟合数据对原数据的重建效率:若CE的取值大于0.75, 则表示拟合模型能很好的描述原始序列的特征; CE的取值为0.36~0.75则表示拟合模型能一定程度上模拟原始数据特征; 当CE< 0.36时, 拟合结果不可信^{[15, 16]}。对于非植被生长覆被类型还将进一步统计分析滤波前后序列最大值、最小值和均值。

本文Hyb-F算法基于Matlab软件平台编程实现, 4种对照方法的滤波结果通过TIMESAT软件获得。对照算法各点初始权重设为1, 移动窗口宽度设为7, 上包络线拟合强度设为2。由Landsat影像直接算得的NDVI序列存在超出理论值域等与实际不符的无效点, 因此, 采用对照方法滤波前将移动窗口长度设为5, 通过设定曲线各点取值、变化量、变化量与变化方向的关系、雪盖指数等指标的阈值, 识别并剔除移动窗口中超出理论值的噪声和部分云、雪噪声, 并以保留下来数据的二次多项式拟合曲线在噪声点的取值代替原始值。

2 结果与讨论

2.1 样本拟合结果直观视觉比较

由于各覆被类型的植被生长状况有所差异, 将各覆被类型分为“ 有植被生长覆被类型” 与“ 非植被生长覆被类型” 两大类进行分析, 从各覆被类型样本中分别选取一个拟合结果接近的样本和一个拟合结果差异较大样本进行直观比较(见图3和图4)。

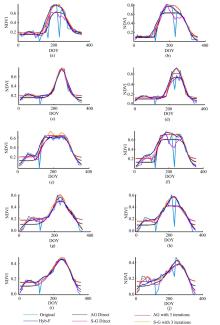	Figure Option View Download New Window
	图3 植被覆盖区域不同重构算法视觉效果对比.Fig.3 Visual comparison of fitted curve of different methods for each land cover type with vegetation

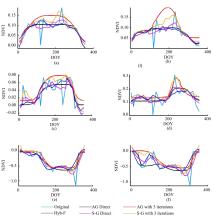	Figure Option View Download New Window
	图4 非植被覆盖区域不同重构算法视觉效果对比Fig.4 Visual comparison of fitted curve of different methods for each land cover type without vegetation

图3(a)和(b)分别为芦苇沼泽样本各算法拟合结果接近和差异较大的曲线, (c)和(d)分别为旱田样本各算法拟合结果接近和差异较大的曲线, (e)和(f)分别为乔木林样本各算法拟合结果接近和差异较大的曲线, (g)和(h)分别为灌木林样本各算法拟合结果接近和差异较大的曲线, (i)和(j)分别为草地样本各算法拟合结果接近和差异较大的曲线。由图3可知, 有植被生长覆被类型, 植被均呈现一年一峰的生长规律, 峰值均出现在8月。草地样本的峰值较低, 介于0.4~0.5之间, 灌木林地样本峰值稍高, 介于0.5~0.6之间, 芦苇沼泽、乔木林地和旱田样本峰值最高, 达到0.7以上。Hyb-F、S-G和AG算法都能平滑NDVI曲线。Hyb-F算法整体上与AG算法和S-G算法的三次迭代运算结果更接近。该算法的异常值判断方案分3步剔除噪声, 植被NDVI曲线峰值保存较好, 峰值处噪声对最终拟合结果影响较小; 剔除异常值后的时间序列各点取值符合植被生长变化规律, 基于此算法得到的重构结果能体现植被的年内整体生长变化特征, 即全局特征。Hyb-F滤波法最终滤波过程由二次S-G滤波完成, 能较好地保留NDVI曲线的细部变化特征。

无迭代过程直接得到的S-G和AG滤波结果受噪声影响大, 尤其是当原始曲线峰值附近存在低值噪声污染时, 拟合曲线的峰值偏低, 存在明显峰值损失。两种算法的迭代方式增加了拟合结果与原始序列的比较过程, 通过调整曲线低值位置的拟合权重来调整重构序列取值。迭代运算能够优化含有低值噪声序列的拟合结果, 但对高值噪声不敏感, 迭代结果趋近时间序列的上包络线。此外, 重设权重时虽识别了低值噪声, 但低值仍然参与运算过程, 影响拟合曲线质量。

图4(a)和(b)分别为盐碱地样本各算法拟合结果较为接近和差异较大的曲线, (c)和(d)分别为城镇工矿建设用地样本各算法拟合结果较为接近和差异较大的曲线, (e)和(f)分别水域样本各算法拟合结果较为接近和差异较大的曲线。由图4可知, 研究区内重度盐碱地、工矿建设用地鲜有植被生长, 年内NDVI取值接近于0, 且无明显变化趋势。重构后的水域样本NDVI时间序列取值普遍为负值, 整体呈现先降低再升高趋势。冬季曲线取值偏高, 可能东北地区冬季水体表面冻结引起的水表反射率变化导致。夏季水体NDVI取值出现低矮波峰, 可能由水面植被生长造成^[17]。对于重度盐碱地和城镇工矿建设用地的理想拟合结果应为接近于0的恒定值, 然而在中等分辨率影像上, 城镇内部绿化区域与建筑物构成混合像元, 盐碱地表层生长的少量植被与出露盐碱地构成混合像元, 使城镇工矿用地和盐碱地在影像分辨率尺度上很难达到绝对纯净, NDVI曲线受植被影响, 但总体应保持原有趋势。对于非植被生长覆被类型(图4), Hyb-F组合滤波法重构的时间序列, 最大值降低, 最小值提高, 在一定程度上削弱了曲线体现出的植被生长规律, 达到平滑曲线的效果, 但仍存在细小波动。AG和S-G三次迭代滤波算法所得结果仍然趋近曲线整体上包络线, 当高值突变噪声存在时, 其对盐碱地(图4(a)(b))、城镇工矿用地(图4(c)(d))的部分样本的滤波结果表现出植被生长的变化规律, 与实际情况不符。对于此类型的NDVI曲线拟合, Hyb-F和AG的直接拟合结果更接近真实情况, AG算法直接拟合效果更佳。

2.2 样本点重构序列指标定量分析

采用不同滤波算法重构各类地表覆被时间序列, 重构结果的精度评价指标如表2所示。表2中前5类覆被类型为有植被生长的覆被类型, 后类为非植被生长覆被类型。AG1和SG1分别表示AG、S-G算法无迭代的直接拟合方式, AG3和SG3分别表示两种算法三次迭代拟合方式, Hyb-F表示本文提出组合滤波算法。表中粗体数字表示各地类拟合结果对应统计指标的最佳取值, 带下划线的数据表示各地类拟合结果对应统计指标的最差取值。

表2 各覆被类型不同滤波算法结果统计指标对比 Table 2 Statistic evaluation of different methods for each land cover type

Hyb-F算法对灌木林地和草地的重构结果子序列与原子序列的相关系数分别为0.9215和0.9158, 与其他种拟合结果相比, RMSE、MAE和MRE的取值最小。Hyb-F算法对灌木林地和草地样本的重构效果最好。AG算法的直接拟合结果对这两种覆被类型的拟合结果精度较差。Hyb-F算法对旱田样本的重构结果与其他算法相比相关系数较小, 但也达到0.9108, 说明Hyb-F重构算法也能构建高质量的旱田NDVI时间序列。在重构旱田数据时, AG算法的效果最好。Hyb-F算法对芦苇沼泽的重构效果最差, 与原子序列的相关系数为0.8036, 在几种算法中相关性最低, RMSE为0.1732, MRE为0.4597, 在几种算法中重构误差最大。然而, 芦苇沼泽的NDVI取值除受植被类型的影响外, 还受到水文条件的制约, 相比于旱地, NDVI曲线变化规律较复杂, 这可能是造成拟合结果偏差较大的原因。Hyb-F算法对乔木林地的重构结果与原子序列的相关系数较低, 仅高于SG3方式的重构结果, 然而, 重构子序列和参考子序列间的偏差较小, 推断Hyb-F算法对乔木林地的重构子序列能够还原原序列中高质量数据, 较低的相关性可能由两子序列同时间点数据差值的方向变化导致。以上结果表明Hyb-F算法能有效模拟植被覆盖区域的NDVI曲线变化趋势。

对于鲜有植被覆盖的重度盐碱地和城镇工矿建设用地样本, 组合滤波法的指标值优于其他种方式, 而对于水域样本的模拟, Hyb-F 组合滤波法所得结果精度最差。非植被生长的覆被类型, 时序曲线的理想值趋于常数, 不能仅通过相关系数、绝对误差和相对误差判断滤波效果, 在分析该类地物时序曲线重构效果时, 还需引入完整时序曲线最大值、最小值、均值指标, 各指标取值如表3所示。其中Original为滤波前的原始时间序列。

表3 非植被生长覆被类型滤波算法结果额外统计指标对比 Table 3 Additional statistic evaluation of different methods for each land cover type without vegetation

由表3可知, 所有的滤波结果都能在一定程度上降低序列最大值, 提高序列最小值, 使NDVI时序数据取值跨度减小, 更趋近于常数, 达到平滑曲线效果。Hyb-F滤波算法对水域的平滑效果最好, 对重度盐碱地和工矿用地的平滑效果仅次于AG1方法。采用Hyb-F算法能有效重构非植被生长的覆被类型的时序数据。

2.3 区域应用

2.3.1 区域应用视觉效果分析

遥感影像云噪声能通过人眼直接识别, 图5为向海自然保护区云污染数据采用Hyb-F滤波前后对比图, 图5(a)和(b)为4月29日厚云污染数据滤波前后对比图, (c)和(d)为9月19日絮状云污染数据滤波前后对比图。从图5可见, 以植被指数时间序列影像为基础, 采用Hyb-F算法重构时序数据, 能识别云噪声点, 并拟合噪声点处数据取值, 滤除影像云层。由图5 (c)和(d)可知, 在无云遮挡区域, 组合滤波算法能有效保持原有数据的取值水平。

	Figure Option View Download New Window
	图5 研究区云污染数据滤波前后对比.Fig.5 Comparison of imagery before and after the regional application of the hybrid filtering algorithm

2.3.2 区域应用指标定量分析

为定量分析Hyb-F算法区域拟合结果, 将一景噪声污染影像的重构结果与获取条件接近的一景高质量参考影像进行对比, 计算定量评价统计指标。由于植被生长速率有限, 对同一样点, 一般假定获取时间间隔在5天内的NDVI值近似相等。Landsat卫星传感器相对稳定, 且研究区为自然保护区, 较少人为干扰, 相邻年份同时期土地利用类型相对固定, 气候条件稳定。选取2015年5月13日与2016年5月15日拍摄影像评价算法区域应用效果, 影像特征见表1。由影像拍摄时间的历史气象数据得知, 两景影像都是晴天获取, 且获取影像时段的气温接近, 符合假设条件, 可近似认为两景影像获取的NDVI取值相等。由于水体具有流动性, NDVI取值不确定度大, 变化迅速, 因此在比较区域应用指标时, 仅计算非水体部分的拟合结果统计指标(见表4)。

表4 Hyb-F算法区域应用效果统计指标 Table 4 Statistic evaluation for the regional application of the hybrid filtering algorithm

将组合算法在整个向海自然保护区应用, 滤波结果与临近参考影像间的相关系数为0.8350, 数据重构效率系数为0.5904, 组合滤波算法能够有效模拟整个区域土地覆被类型的NDVI实际情况。

3 结论

利用Landsat8影像构建NDVI时间序列, 并采用Hyb-F组合滤波方案剔除序列噪声, 重构NDVI时间序列曲线。与常用的S-G局部滤波算法与AG半全局拟合算法相比, Hyb-F算法有以下特点:

(1)能更有效地全面识别序列全局和局部异常点, 提高曲线拟合精度, 减少低值异常点引起的峰值损失。

(2)Hyb-F算法兼顾时间序列曲线的局部特征和全局变化趋势, 对于有植被生长的覆被类型, 滤波结果与原始数据相关性较大, 样本的重构结果子序列与纯净数据子序列间的相关度达0.8以上, 对草地和灌木林地样本的重构精度最高。由于水文因素影响, 芦苇沼泽NDVI的变化较为复杂, 组合式滤波法的拟合结果精度较差。

(3)对于非植被生长覆被类型, 该算法能有效滤除序列的波动信息, 平滑时序曲线。

本研究主要的数据源为Landsat8 OLI多光谱影像, 在今后的研究中可基于其他类型数据继续实验, 收集研究区植被物候观测数据, 将物候信息提取能力引入到算法精度评价方案中, 并尽量获取野外实测的NDVI值, 得到更精确、更全的面验证结果。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Zhou J, Jia L, Menenti M, et al. On the performance of remote sensing time series reconstruction methods—A spatial comparison[J]. Remote Sensing of Environment, 2016, 187: 367-384. [本文引用:1]
[2]	Geng L, Ma M, Wang X, et al. Comparison of eight techniques for reconstructing multi-satellite sensor time-series NDVI data sets in the heihe river basin, China[J]. Remote Sensing, 2014, 6(3): 2024-2049. [本文引用:3]
[3]	刘亚南, 肖飞, 杜耘. Logistic函数方法拟合多时序NDVI数据的改进研究[J]. 遥感技术与应用, 2015, 30(4): 737-743. Liu Ya-nan, Xiao Fei, Du Yun. Improved logistic model for fitting time-series NDVI data[J]. Remote Sensing Technology and Application, 2015, 30(4): 737-743. [本文引用:2]
[4]	Jonsson P, Eklundh L. Seasonality extraction by function fitting to time-series of satellite sensor data[J]. IEEE Transactions on Geoscience & Remote Sensing, 2002, 40(8): 1824-1832. [本文引用:2]
[5]	Jönsson P, Eklundh L, Timest. A program for analyzing time-series of satellite sensor data[J]. Computers & Geosciences, 2004, 30(8): 833-845. [本文引用:2]
[6]	Zhou J, Jia L, Menenti M. Reconstruction of global MODIS NDVI time series: Performance of harmonic analysis of time series (HANTS)[J]. Remote Sensing of Environment, 2015, 163: 217-228. [本文引用:1]
[7]	Moreno Á, Garcíaharo F, Martínez B, et al. Noise reduction and gap filling of fAPAR time series using an adapted local regression filter[J]. Remote Sensing, 2014, 6(9): 8238-8260. [本文引用:1]
[8]	张霞, 李儒, 岳跃民, 等. 谐波改进的植被指数时间序列重建算法[J]. 遥感学报, 2010, 14(3): 437-447. Zhang Xia, Li Ru, Yue Yue-min, et al. Improved algorithm for reconstructing vegetation index image time series based on fourier harmonic analysis[J]. Journal of Remote Sensing, 2010, 14(3): 437-447. [本文引用:2]
[9]	刘珺, 田庆久, 黄彦, 等. 黄淮海夏玉米物候期遥感监测研究[J]. 遥感信息, 2013, 28(3): 85-90. Liu Jun, Tian Qing-jiu, Huang Yan, et al. Monitoring phenology of summer maize in huang-huai-hai using remote sensing technology[J]. Remote Sensing Information, 2013, 28(3): 85-90. [本文引用:1]
[10]	Liang S, Ma W, Sui X, et, al. Extracting the spatiotemporal pattern of cropping systems from NDVI time series using a combination of the spline and HANTS algorithms: a case study for shand ong province[J]. Canadian Journal of Remote Sensing, 2017, 43(1): 1-15. [本文引用:1]
[11]	卞建民, 林年丰, 汤洁. 吉林西部向海湿地环境退化及驱动机制研究[J]. 吉林大学学报: 地学版, 2004, 34(3): 441-444, 458. Bian Jian-min, Lin Nian-feng, Tang Jie. The environment degradation and its driving mechanism of Xianghai wetland in the west of Jilin province[J]. Journal of Jilin University (Earth Science Edition), 2004, 34(3): 441-444, 458. [本文引用:1]
[12]	李荣平, 周广胜, 郭春明, 等. 1981-2005年中国东北榆树物候变化特征及模拟研究[J]. 气象与环境学报, 2008, 24(5): 20-24. Li Rong-ping, Zhou Guang-sheng, Guo Chun-ming, et al. Phenology characteristics of ulmus pumila and its simulation from 1981 to 2005 in Northeast China[J]. Journal of Meteorology and Environment, 2008, 24(5): 20-24. [本文引用:1]
[13]	唐蕴, 王浩, 严登华. 向海自然保护区湿地生态需水研究[J]. 资源科学, 2005, 27(5): 101-106. Tang Yun, Wang Hao, Yan Deng-hua. Wetland ecological water demand in Xianghai natural reserve[J]. Resources Science, 2005, 27(5): 101-106. [本文引用:1]
[14]	周增光, 唐娉. 基于质量权重的Savitzky-Golay时间序列滤波方法[J]. 遥感技术与应用, 2013, 28(2): 232-239. Zhou Zeng-guang, Tang Pin. VI-quality-based savitzky-golay method for filtering time series data[J]. Remote Sensing Technology and Application, 2013, 28(2): 232-239. [本文引用:1]
[15]	Wu M, Zhang X, Huang W, et al. Reconstruction of daily 30 m data from HJ CCD, GF-1 WFV, land sat, and MODIS data for crop monitoring[J]. Remote Sensing, 2015, 7(12): 16293-16314. [本文引用:1]
[16]	Li X, Shen H, Li H, et al. Patch matching-based multitemporal group sparse representation for the missing information reconstruction of remote-sensing images[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(8): 3629-3641. [本文引用:1]
[17]	李天祺, 朱秀芳, 潘耀忠, 等. 环境星NDVI时间序列重构方法研究[J]. 遥感信息, 2015(1): 58-65. Li Tian-qi, Zhu Xiu-fang, Pan Yao-zhong, et al. NDVI time-series reconstruction methods of China's HJ satellite imagery[J]. Remote Sensing Information, 2015(1): 58-65. [本文引用:1]

2016

0.0

... 然而由卫星直接获取的遥感数据得到的NDVI时间序列中存在来自云、冰雪、阴影、气溶胶双向反射等多种噪声,在应用前应去除噪声,重构时间序列^[1,2,3] ...

2014

0.0

... 不同重构方法对不同区域或不同数据源的适用性不同,多位学者提出了各算法的对比结果,但各算法优劣目前并无定论^[2] ...

... 目前已有学者对一些单一类型数据重构算法进行改进^[3,8],或同时利用两类滤波算法构建组合式滤波算法^[2,9,10],提高NDVI时间序列重构精度和重构过程的自动化程度,但相关研究仍存在以下局限 ...

2015

0.0

. 2015, 30(4):737-743 DOI:doi:10.11873/j.issn.1004-0323.2015.4.0737

Improved logistic model for fitting time-series NDVI data

Logistic函数方法拟合多时序NDVI数据的改进研究

Liu Ya-nan , Xiao Fei , Du Yun

刘亚南, 肖飞, 杜耘

单Logistic函数曲线拟合法是NDVI时间序列重建及物候遥感中关键物候期划分的重要方法之一。虽然该方法不需要设定阈值或经验系数、较适应于不同环境区域的物候遥感监测,但是在山区NDVI噪音较大的情形下,其拟合精度仍会受到较大影响。选取秦岭中部山区为研究区,在分析了多年NDVI时间序列数据特征基础上,利用山区NDVI数据序列最大值相对于最小值更为稳定的特性,对传统单Logistic模型求解方法进行改进,采用更为稳定的参数构建模型以提高NDVI时间序列重建的精度。基于秦岭样区MODIS NDVI多年遥感数据,分别在保持植被生长季特征能力和保留高质量原始真值程度两方面对原方法与改进方法的计算结果进行比较。研究表明改进的方法在上述两个方面都具有更好的效果。在植被指数噪音较大的山区,改进的方法对NDVI时间序列重建表现出更好的适用性,可为复杂的山区物候遥感相关研究提供参考。

2002

0.0

... 基于全局或半全局数据的非对称高斯拟合法、双逻辑函数拟合法^[4,5]和时间序列谐波分析法^[6,7]等 ...

... α(t)和 β(t)为由0到1平滑过渡的截断函数^[4,5] ...

2004

0.0

... 基于全局或半全局数据的非对称高斯拟合法、双逻辑函数拟合法^[4,5]和时间序列谐波分析法^[6,7]等 ...

... α(t)和 β(t)为由0到1平滑过渡的截断函数^[4,5] ...

2015

0.0

... 基于全局或半全局数据的非对称高斯拟合法、双逻辑函数拟合法^[4,5]和时间序列谐波分析法^[6,7]等 ...

2014

0.0

... 基于全局或半全局数据的非对称高斯拟合法、双逻辑函数拟合法^[4,5]和时间序列谐波分析法^[6,7]等 ...

2010

0.0

. 2010, 14(3):437-447 DOI:doi:10.11834/jrs.20100303

Improved algorithm for reconstructing vegetation index image time series based on fourier harmonic analysis

谐波改进的植被指数时间序列重建算法

Zhang Xia , Li Ru , Yue Yue-min

张霞, 李儒, 岳跃民

This paper, based on Fourier-transform-based Harmonic Analysis Algorithm, proposes an improved algorithm to overcome the drawback of artificially setting key parameters and to reconstruct high-quality time-series data. Firstly, outlier detection algorithm, instead of threshold setting method, is used to find unreasonable data points before curve fitting. Then, regarding the inherent phenological regulation for each land cover, Numbers of Frequency (NOF) is calculated pixel by pixel by polynomial fitting, which is more reasonable than setting a unique global NOF for the whole scene which contains complex land cover types. Fitting-effect Index, instead of manually setting one fitting tolerance, is employed to decide automatically when to terminate the iteration. The improved method is validated by the MODIS_EVI time series of Huabei plain of 2003. The widely used Harmonic Analysis of Time Series (HANTS) is chosen as a comparison. The result shows that both of the two methods can reflect the phenological regulations of land covers, the reconstructed EVI temporal profile of single-season crop-land (e.g. cotton) takes on one peak pattern, and those of double-season cropland and inland water take on double peak pattern and low-steady curve. But the improved method performs better in tracking the change tendency of the original curve. More-over, the peak time and peak value of croplands are mostly consistent with the original curve, which will be useful for VI-based crop yield prediction.

提出一种基于傅里叶谐波分析的改进算法, 引入异常值检测算法, 检测拟合过程中的异常值, 增加数据拟合的真实性; 迭代前动态估算出待处理序列点的峰值个数(即频数), 解决整个区域预设单一频数的不合理性; 引入拟合影响因子, 自动控制迭代终止条件, 避免传统方法中人为设置阈值导致的不确定性。利用2003年华北平原MODIS_EVI时间序列图像验证表明, 较之HANTS算法, 改进算法能够有效修正噪声污染像元值, 修正后的EVI时序曲线更能反映地物内在的物候变化规律, 并能够更好地保真原始曲线上的特征(点), 如作物EVI最大值、最小值出现的时间和大小关系。

... 若统计量超过临界值的范围,则该点为异常点^[8] ...

2013

0.0

. 2013, 28(3):85-90 DOI:doi:10.3969/j.issn.1000-3177.2013.03.015

Monitoring phenology of summer maize in huang-huai-hai using remote sensing technology

黄淮海夏玉米物候期遥感监测研究

Liu Jun , Tian Qing-jiu , Huang Yan

刘珺, 田庆久, 黄彦

摘　要：以黄淮海为研究区，基于MODISEVI植被指数遥感数据，利用Logistic模型对夏玉米关键物候期（苗期、拔节期、抽雄期、成熟期）进行了监测。使用地面物候观测数据对监测结果加以检验，并与其他常见的遥感监测模型进行了比较。结果表明：研究监测结果总体误差小于±6天，误差较大的区域多出现在地势较高，种植结构较复杂的地区。研究结果可为进行全球气候变化研究提供依据。

2017

0.0

2004

0.0

. 2004, 34(3):441-444,458

The environment degradation and its driving mechanism of Xianghai wetland in the west of Jilin province

吉林西部向海湿地环境退化及驱动机制研究

Bian Jian-min , Lin Nian-feng , Tang Jie

卞建民, 林年丰, 汤洁

... 保护区内多种珍稀野生动植物繁育,多样生态景观共存^[11] ...

2008

0.0

. 2008, 24(5):20-24

Phenology characteristics of ulmus pumila and its simulation from 1981 to 2005 in Northeast China

1981-2005年中国东北榆树物候变化特征及模拟研究

Li Rong-ping , Zhou Guang-sheng , Guo Chun-ming

李荣平, 周广胜, 郭春明

... 向海自然保护区内的地表覆被类型如图1(b)所示,主要是以蒙古黄榆、大果榆为主的灌木林地,杨树为主的乔木林地,以芦苇、香蒲为主的沼泽湿地,以羊草为主的草地,以玉米田为主的耕地,大片水域,出露的重度盐碱地和零星分布的城镇工矿建设用地^[12,13] ...

2005

0.0

. 2005, 27(5):101-106 DOI:doi:10.3321/j.issn:1007-7588.2005.05.016

Wetland ecological water demand in Xianghai natural reserve

向海自然保护区湿地生态需水研究

Tang Yun , Wang Hao , Yan Deng-hua

唐蕴, 王浩, 严登华

Xianghai Wetland is located in the semiarid western part of Songnen Plain，where natural precipitation can’t meet ecological water demand of the wetland.Wetland ecological water demand refers to water consumption for maintenance of normal structural and functional behavior of the wetland ecosystem.Scientific accounting of the water quantity can provide major basis for reasonable wetland management and conservation.Xianghai Natural Reserve is located in Jilin province，which belongs to inland wetland and water ecosystem.Owing to natural and manmade factors especially reduced waterinflow，Xianghai Wetland is facing serious threatening problem.This paper analyzed variation features of the wetland in Xianghai Natural Reserve at the end of last century by using Landsat TM remote sensing images in 1996 and 2000 and applying ArcGis8.3 as a key data processing platform.The result indicates that landscape composition in Xianghai Natural Reserve in recent 5 years is as follows:25.88% of grassland，28.7% of wetland，22.2% of barren land，11.24% of forestland，11.07% of farmland，and 0.89% of the other land uses.Lakes and swamps are major components of Xianghai wetlands.The coverage of wetland landscape remains as 300 km.2，among which lakes and swamps amount toe 96 km.2 and 198 km.2 respectively.As a result，ecological water demand of Xianghai wetlands include two parts，namely lake ecological water demand and swamp ecological water demand.Lake ecological water demand refers to water consumption that maintains normal ecological function，and includes quantity of surface water evaporation and water seepage.Swamp ecological water demand refers to water consumption that maintains normal structure and function of the swamp，which mainly includes quantity of swamp plants transpiration and water surface evaporation.Wetland ecological water demand is 340 million m3 and 365 million m3 in average year and dry year，respectively.Among which water demand during April and August is about 78% of a year.It is a fundamental route to synthetically manage and adjust water resources in the catchments in order to solve water shortage problem of the Xianghai Wetland.

湿地生态需水是指维持湿地生态系统结构和功能正常所需要消耗的水量，对其进行科学核算可为湿地的科学管理和保护提供重要依据。近年来，受自然和人为因素影响特别是来水量的减少，向海湿地面临严重威胁。本文以1996年和2000年两期Landsat TM遥感影像为数据源，对上个世纪末期向海自然保护区湿地的变化特征进行了剖析；在此基础上，采用水量平衡的原理，对不同水平年向海湿地生态需水进行分析研究。结果表明，保护区湖沼湿地景观面积基本保持在300km2，占保护区总面积的28.7%。在平、枯水年湿地生态需水量分别是3400亿m3和36.5亿m3，其中4月～8月需水量约占全年需水量的78%。向海湿地位于松嫩平原西部，属半干旱地区，天然降水不能满足湿地的生态需水要求，对流域水资源进行综合管理和调度是解决向海湿地水源问题的根本途径。

2013

0.0

. 2013, 28(2):232-239 DOI:doi:doi:10.11873/j.issn.1004-0323.2013.2.232

VI-quality-based savitzky-golay method for filtering time series data

基于质量权重的Savitzky-Golay时间序列滤波方法

Zhou Zeng-guang , Tang Pin

周增光, 唐娉

归一化植被指数(NDVI)时间序列数据因含有大量噪声,给其应用带来诸多不便,甚至产生错误结果。自适应Savitzky-Golay滤波器能够有效地抑制突降噪声,但在对高值噪声的抑制和突降非噪声数据的保护方面存在不足。将MODIS VI产品中的质量因子作为权重,提出基于质量权重的Savitzky-Golay滤波方法,经验证该方法能够保持高质量NDVI数据的稳定性和相关性,并能够有效抑制噪声的影响。

... 当高质量数据在整个时间序列所占比例较高时,S-G算法能够过滤序列噪声,较细致地描述序列局部特征^[14] ...

2015

0.0

... 36时,拟合结果不可信^[15,16] ...

2016

0.0

... 36时,拟合结果不可信^[15,16] ...

2015

0.0

. 2015, (1):58-65 DOI:doi:10.3969/j.issn.1000-3177.2015.01.010

NDVI time-series reconstruction methods of China's HJ satellite imagery

环境星NDVI时间序列重构方法研究

Li Tian-qi , Zhu Xiu-fang , Pan Yao-zhong

李天祺, 朱秀芳, 潘耀忠

利用目前时间序列曲线重构中较为常用的非对称高斯函数拟合、Double-Logistic曲线拟合、S-G滤波和时间序列谐波分析法对环境星NDVI时间序列进行重构处理。分析了上述4种植被指数时间序列重构方法对环境星数据的适用性。实验结果表明,对于环境星数据,在4种方法中非对称高斯函数拟合、Double-Logistic曲线拟合法更适用于对植被地物的时间序列进行重构,对照参考数据,其重构曲线对植被物候的表达有较高的一致性;而时间序列谐波分析法对原始数据的扰动最小,适用于非植被地物的时间序列重构;S-G滤波在4种方法中的重构效果最差。

... 夏季水体NDVI取值出现低矮波峰,可能由水面植被生长造成^[17] ...