引用本文
张曼, 施树明. 典型汽车运行工况的状态转移特征分析[J].吉林大学学报（工学版）, 2018,48(4): 1008-1015
ZHANG Man, SHI Shu-ming. Analysis of state transition characteristics for typical vehicle driving cycles[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 1008-1015  
Doi:10.13229/j.cnki.jdxbgxb20170301
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有 吉林大学学报编辑部
典型汽车运行工况的状态转移特征分析
张曼, 施树明
吉林大学 交通学院,长春 130022
通讯作者:施树明(1965-),男,教授,博士生导师.研究方向:车辆运行仿真.E-mail:shishuming@jlu.edu.cn

作者简介:张曼(1990-),女,博士研究生.研究方向:汽车运行工况设计.E-mail:m15104682686@163.com

基金:国家自然科学基金项目(51475199).
摘要

针对当前运行工况研究仅选取某些特征参数作为特征、缺乏对工况状态转移特征分析的不足,本文在提取典型工况特征参数的基础上,运用主成分分析和 K均值聚类获得行驶特征较明显的3类工况,并分析各类工况状态转移转移矩阵(TPM)的状态、转移概率和特征值。结果表明:各类TPM状态、转移概率的分析与各类典型工况特征参数的分析一致;特征值对高速、混合和城市道路运行工况的工况生成效率存在本质影响,揭示了运行工况设计中构建两参数TPM的合理性。

关键词: 车辆工程; 状态转移概率矩阵; 主成分分析; K均值聚类; 典型运行工况
中图分类号:U461.1 文献标志码:A 文章编号:1671-5497(2018)04-1008-08
Analysis of state transition characteristics for typical vehicle driving cycles
ZHANG Man, SHI Shu-ming
College of Transportation, Jilin University, Changchun 130022, China
Abstract

In current research of vehicle driving cycles only some parameters are selected as characteristics of the driving cycles, which lacks the analysis of the characteristics of driving cycle state transition. To solve this problem, based on the characteristic parameters extracted from typical driving cycles, this paper adopts the principal component analysis and K-means clustering to obtain three kinds of typical driving cycles, which represent the vehicle driving characteristics under different traffic conditions. The state, transition probability and eigenvalues of the state Transition Probability Matrixes (TPM) under the typical driving cycles are analyzed, and the analysis results are consistent with that of the characteristic parameter analysis under three kinds of typical driving cycles. It is shown that the eigenvalues essentially influences the efficiency of cycle generation of highway, suburb and city roads, revealing the reasonability of construction two-parameter TPM in designing driving cycles.

Keyword: vehicle engineering; state transition probability matrix; principal component analysis; K-means clustering; typical driving cycles
0 引 言

汽车运行工况在车辆和交通领域起到重要作用。研究工况状态转移特征对工况的影响有助于从本质上表达和理解工况, 有利于指导和拓展运行工况的工程应用。

Bata等[1]通过对比不同的重型车测试工况, 分析了速度和加速度的联合概率分布(VA分布)的特征, 指出在考虑汽车运行工况代表性时, VA分布矩阵在不同工况的对比上起到关键作用; Andre[2]基于VA原理示意图, 分析了时间占比分别为50%、75%和90%的工况, 强调VA分布原理图可作为分析工况的有效工具; Lin[3]利用马尔科夫链方法设计工况, 结合VA相关特征参数匹配原始数据设计了代表性工况。在评价汽车运行工况时, 文献[4, 5]将VA分布一致性作为设计目的, 使用VA分布相关特征参数(例如平均速度、怠速比例等)作为工况的特征进行评价。尽管利用VA分布相关参数作为工况特征的分析方法较为普遍, 但是这种分析方式没有考虑到汽车运行工况的状态转移本质特征。随着运行工况为马尔科夫链本质的证明, 对工况特征的研究开始转向对状态转移矩阵的研究, Shi等[6]证明了在小尺度内(1 s), 汽车运行工况本质上是马尔科夫过程, 揭示了VA分布与速度加速度二维状态转移矩阵的关系; Liu等[7]利用马尔科夫链方法设计电动车的瞬态工况, 指出在高峰期条件下, 运行工况状态存在更多转移的可能性从而使工况具有更多不确定性。但研究仅简单地对比了自由流和高峰期的状态转移矩阵; Yue等[8]利用牵引车试验数据, 分析了坡度具有马尔科夫性, 构造了速度、加速度和坡度的3参数状态转移矩阵, 但仍未对工况状态转移特性进行深入分析。

为了全面剖析汽车运行工况, 以典型汽车运行工况作为总体样本, 提取特征参数, 采用主成分分析与 K均值聚类算法[9, 10]对典型汽车运行工况进行分类, 进而分析各类工况的状态转移特征。

1 算法基础
1.1 主成分分析

有 m个待分析的样本, 每个样本有n个特征, 把这m个样本的n个特征构成的向量矩阵转化成标准矩阵X:

X=x11x12…x1nx21x22…x2n︙︙︙xm1xm2…xmn=X1, X2, …, Xn(1)

然后计算标准矩阵的协方差矩阵(即相关矩阵), 求解相关矩阵的一系列特征值 λ以及与λ对应的单位正交化特征向量e1, e2, …, en, 如式(2)所示:

[e1, e2, …, en]=e11e12…e1ne21e22…e2n︙︙︙en1en2…enn(2)

计算第i个特征值的贡献率λ i /∑j=1nλj, 贡献率越大表示特征值概括原来特征反映信息的能力越强。 ∑r=1lλ r /∑j=1nλj为前l个特征值的贡献率之和, 当累计贡献率 ∑r=1lλ r /∑j=1nλj≥ 85%时, 选择前l个特征值所反映的信息就基本能满足工程应用要求。将选择的前l个特征值的单位特征向量与标准化样本特征矩阵中每个样本的对应特征值相乘, 得到各样本的主成分, 如式(3)所示:

Fk=eTk·X=ek1·X1+ek2·X2+…+ekn·Xn(3)

式中: k=1, 2, …, l。

每个样本都有 l个主成分, 这l个主成分可以代替原特征表达绝大部分信息, 且为互不相关的新特征, 便可通过分析样本的主成分代替对样本原特征的分析。

1.2 K均值聚类

K均值聚类, 又叫快速聚类[10], 选定 k类和k个初始聚类中心, 按最小距离原则分配各样本, 之后不断计算聚类中心和调整各样本的类别, 使类内具有较高的相似度, 而类间的相似度较低。具体为:

(1)针对 n个样本按照某种原则选取k个样本作为初始聚类中心(z1, z2, …, zk)。

(2)用欧式距离将剩余任意样本 xi赋给距离它们最近的簇中心。欧式距离是指两个样本所有 n个变量值之差平方和的平方根, 即:

$d_{x, y}=\sqrt{\sum\limits_{i=1}^{s}(x_{i}-y_{i})^{2}}$(4)

式中: xi是样本x的第i个变量的变量值; yi是样本y的第i个变量的变量值。

(3)重新计算每个簇中对象的平均值, 用此平均值作为新的聚类中心。

(4)重复以上步骤, 直到聚类中心不再发生变化。

2 基于特征参数的典型运行工况

为了分析不同类别典型汽车运行工况的状态转移特征, 本文用汽车运行工况时间序列的常用11个特征参数对工况进行分类。

首先, 确定提取的11个特征参数, 包括加速比例(Pa)、减速比例(Pd)、匀速比例(Pc)、怠速比例(Pi)、最大速度(Vmax)、平均速度(Vm)、最大加速度(Amax)、最小加速度(Amin)、加速段平均加速度(Aam)、减速段平均减速度(Adm)、平均行驶速度(Vdm)。

然后, 选取国内外典型运行工况, 包含82个不同路况、不同车型、不同用途的典型工况, 来源于Advisor软件中测试工况数据库和DieselNet网站的所有整车测试工况数据库[11]以及部分国内代表性工况。

接下来, 基于特征参数对典型运行工况进行分类。利用Matlab分别统计各个工况的11个特征参数, 得到一个特征参数(行)乘以样本数量(列)的矩阵, 如表1所示。

表1 典型工况的常用特征参数 Table 1 Characteristic parameters of typical driving cycles

已知特征参数之间存在一定的相关性, 存在重叠信息, 而利用主成分分析可以用较少的变量表达较多的信息, 且主成分之间相关性为零。对所有样本的全部特征值参数进行主成分分析, 得到前10个主成分 Mi, 其中i=1, 2, …, 10。各个主成分的贡献率和累积贡献率见表2。

表2 主成分贡献率和累积贡献率 Table 2 Principal component contribution and cumulative contribution

前 m个主成分的累积贡献率为 ∑k=1mλ k /∑k=110λk, 其中 λk表示第k个主成分的特征值, 累计贡献率表明M1, M2, …, Mm综合所有原始变量的能力。通常选取使得累积贡献率达到85%左右的前 m个主成分代表所有原始变量进行分析。通过表2可以看出, 前4个主成分特征值的累积贡献率达到87.25%, 故选取前4个主成分进行分析。在主成分分析的同时也可以得到各工况样本在前4个主成分上的得分, 如表3所示。

表3 各主成分得分 Table 3 Scores of each principal component

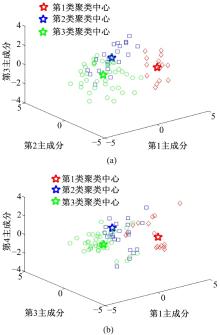
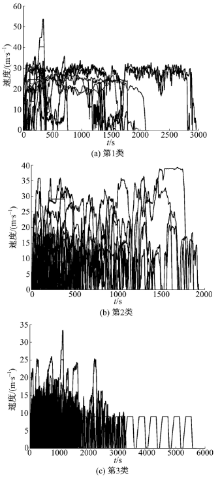
利用 K均值聚类对4个主成分分类, 聚类结果如图1所示。从图1可知, 82个工况样本被分成3类, 具体详见附录。3类结果中, 第1类用菱形表示, 包括17个样本; 第2类用方框表示, 包括22个样本; 第3类用圆圈表示, 包括43个样本, 星型分别代表各类的聚类中心。不同主成分表明了典型工况得到了较为清晰的分类。

图1 典型工况的K均值聚类结果Fig.1 Result of K-means clustering for typical driving cycles

每类典型汽车运行工况的运行速度和时间序列如图2所示。分析可知, 第1类为典型的高速工况, 包含HWFET、HHDDT-Speed-Cruise-Mode等工况; 第2类为典型混合工况, 例如CWTVC、WLTP等工况, 高低混合速度特征明显; 第3类包含众多的城市工况, 例如Braunschweig、NYCC和乘用车启停等工况, 低中速特征明显。

图2 三类典型工况的运行速度和时间序列图Fig.2 Velocity-time series of three kinds of typical driving cycles

3类工况平均特征参数统计如表4所示。第1类加速比例和减速比例较低, 匀速比例最高, 怠速比例最小, 平均速度较高, 体现了高速工况特征; 第2类怠速比例和平均速度较高, 代表了混合工况的特征; 第3类加速和减速比例较大, 平均速度和匀速比例最低, 怠速比例最高, 体现了城市特征。综上, 3类工况行驶特征分类明显。

表4 三类典型工况的特征参数平均值 Table 4 Characteristic parameters average value of three kinds of typical driving cycles
3 典型工况的状态转移特征分析
3.1 状态转移矩阵的计算

求解马尔科夫状态转移概率矩阵有很多方法, 本文采用文献[7]的方法。首先定义工况的状态。为满足马尔科夫链要求状态离散的条件, 设定速度和加速度步长分别为0.5 m/s和0.5 m/s2, 采用蛇形编码方式, 定义速度、加速度的两参数状态。速度的一维编码定义为速度的单参数状态, 速度和加速度的二维网格编码定义速度、加速度的两参数状态。然后, 计算状态转移矩阵。利用最大似然估计原理[12], 采用Matlab编程, 统计状态转移频数矩阵, 最终计算状态转移概率矩阵[3], 如式(5)所示:

P=p11p12…p1np21p22…p2n︙︙︙pn1pn2…pnn, i, j∈S(5)

式中: pij=Nij/Ni为状态si到状态sj的转移概率; Nij为状态si到状态sj的转移频数; Ni= ∑j=1nNij; S为状态空间。

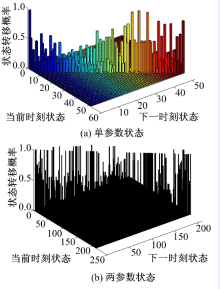
按照以上状态转移矩阵的计算方法, 得到如图3所示的北京工况的单参数和两参数TPM。其中 X轴表示当前时刻状态, Y轴表示下一时刻状态; Z轴表示当前时刻状态转移到下一时刻状态的概率。

图3 北京工况状态转移矩阵三维图Fig.3 Three-dimensional state transition probability matrix of Beijing cycle

3.2 典型工况状态转移特征对比分析

为分析不同类典型工况的状态转移特征, 按照上节计算方法, 分别统计出单参数和两参数的状态转移概率矩阵。从以下两方面分析各类典型工况状态转移特征。

状态转移矩阵由汽车运行工况直接统计得到, 既可以表达状态信息又可以表达状态转移动态信息。在TPM状态、转移概率方面, 图4为各类典型工况的单参数和两参数TPM, 其中实圆圈的大小代表状态转移概率的大小。尽管汽车运行工况的马尔科夫性决定了TPM中当前时刻状态只能向有限个状态转移, 从而不同类TPM具有相似趋势特征, 但是不同类TPM在状态、状态转移概率上仍存在明显区别。

图4 三类典型工况的状态转移矩阵Fig.4 TPMs of three kinds of typical driving cycles

图4(a)组单参数TPM中, 第3类TPM最小状态(对应工况的速度最小也即怠速状态)的自身转移概率最大, 而第1类TPM最小, 这与第3类城市道路工况中平均怠速比例最大、第1类高速公路工况平均怠速比例最小现象一致。此外, 根据单参数和两参数TPM的关系, 图4(a)中最小状态分别对应着图4(b)中第335个状态、第302个状态和第205个状态, 同理可得以上分析; 第1类中高状态转移概率很最大, 低状态转移概率较小, 第2类高状态转移概率较大, 低中状态的状态转移概率较小, 第3类低中状态转移概率很大, 高速状态转移概率最低, 这与第1类典型工况具有高速特征, 第2类工况具有混合工况特征, 第3类工况具有城市低速特征的分析一致; 图4(b)两参数TPM中, 第1类TPM自身状态转移(对角线上)概率最大, 第2类其次, 第3类最小, 这与高速公路工况匀速比例最大, 混合工况次之, 城市道路工况最小的分析相一致。综上, 不同典型工况的状态转移矩阵在状态、转移概率上存在明显差别, 其分析与各类典型工况特征参数分析一致。

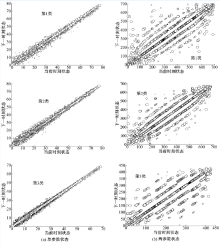
在不同类典型工况TPM的特征值方面, 图5和图6给出了3类典型工况的单参数和两参数状态转移矩阵的前几个特征值。图中相同颜色表示同一类工况TPM的特征值, 不同线型表示第几特征值(特征值由大到小排列, 例如第一特征值表示最大特征值, 第二特征值表示第二个最大特征值, 以此类推)的分布。

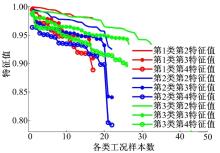
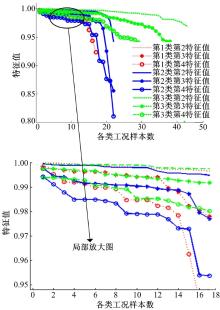图5 三类单参数状态转移矩阵特征值Fig.5 Eigenvalues of single-parameter TPMs of three kinds of typical driving cycles

图6 三类两参数状态转移矩阵特征值Fig.6 Eigenvalues of two-parameter TPMs of three kinds of typical driving cycles

由马尔科夫链随机过程已知其全部特征值的绝对值必介于零和1之间(包含1)[13], 且第1特征值和第2特征值具有明确的物理意义。第1特征值一定为1, 且其单位特征向量对应着马尔科夫链的平稳分布, 也即极限分布[14]。第2特征值与马尔科夫链过程的收敛程度密切相关[13, 15, 16], 即第2特征值越大, 马尔科夫链收敛到平稳分布的速度越慢, 反之越快。目前第3、4等特征值的物理含义仍在研究中。本文着重分析第2、3和4特征值的数值大小, 以此分析不同类工况状态转移矩阵收敛性、特征值趋势以及特征值对汽车运行工况本质上的影响。

观察图5和图6可以发现, 同类工况单参数和两参数状态转移矩阵的第2、3和4特征值, 均呈现衰减趋势, 且两参数状态转移矩阵的特征值衰减趋势较快。不同类工况状态转移矩阵下, 同一第几特征值也存在着衰减程度上的差别。

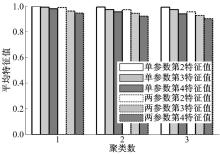
图7利用特征值的平均值分析不同类工况特征值的衰减程度。依次统计了每一类第2、3和4特征值的平均值, 其中同一颜色表示每一类工况状态转移矩阵的平均特征值, 同一颜色下不同线型对应单参数和两参数状态转移矩阵的平均特征值。观察发现, 整体上, 两参数状态转移矩阵的平均特征值(除去第1特征值)要小于单参数对应的平均特征值, 说明了同一类典型工况下, 单参数TPM较两参数的TPM较难收敛到极限分布; 无论单参数还是两参数TPM的平均特征值(除去第1特征值), 按照大小依次降低分别对应着第1类、第2类和第3类工况, 说明了具有高速特征的第1类典型工况收敛速度最慢, 而具有城市低速特征的第3类典型工况收敛速度最快, 具有混合特征的第2类典型工况收敛速度介于两者之间。

图7 三类状态转移矩阵平均特征值Fig.7 Average eigenvalues of TPMs of three kinds of typical driving cycles

基于以上不同类TPM特征值衰减程度的分析讨论特征值对运行工况的本质影响。已知马尔科夫链第1特征值的单位特征向量对应着汽车运行工况的平稳分布[6]。最大特征值相同且均为1, 故工况的平稳分布不受最大特征值的影响。分析知第2特征值影响运行工况马尔科夫链的收敛性, 而工况收敛性主要表现在工况设计过程中。

在设计汽车运行工况时, 代表性工况要求与原始数据库在VA分布(运行工况的平稳分布)具有一致性, 由图7分析可知, 两参数状态转移矩阵更易收敛到平稳分布(VA分布), 所以当使用马尔科夫链方法设计工况时, 构建两参数状态转移矩阵生成代表性工况的过程本质上更具合理性; 同理, 因为高速道路工况收敛速度最慢, 那么高速公路代表性运行工况的生成效率本质上要低于一般公路和城市道路代表性工况。

4 结束语

在分类典型运行工况基础上, 全面剖析了各类工况状态转移特征, 分析结果表明:各类状态转移矩阵在状态和转移概率上存在明显差别, 状态转移矩阵表达的工况特征与时间序列特征参数表达的一致; 第2特征值的大小影响工况设计的收敛速度, 构建两参数的状态转移矩阵更加合理, 收敛速度更快; 具有高速特征典型工况比具有中低速特征典型工况收敛到平稳分布的能力差。受工况状态转移矩阵第2特征值的影响, 基于马尔科夫链方法设计速度和加速度两参数高速公路代表性工况长达几十小时, 生成工况的VA分布相关系数依然很难达到90%以上, 因此, 如何提高运行工况设计效率是下一步研究的重点内容。

附录 三类典型工况

The authors have declared that no competing interests exist.

参考文献
[1] Bata R, Yacoub Y, Wang W, et al. Heavy duty testing cycles: survey and comparison[C]∥SAE Paper, 942263. [本文引用:1]
[2] Andre M. Driving cycles development: characterization of the methods[C]∥SAE Papers, 961112. [本文引用:1]
[3] Lin J. A Markov process approach to driving cycle development[D]. Davis: University of California, 2002. [本文引用:2]
[4] Hung W T, Tam K M, Lee C P, et al. Comparison of driving characteristics in cities of Pearl River Delta, China[J]. Atmospheric Environment, 2005, 39(4): 615-625. [本文引用:1]
[5] 刘志华, 葛蕴珊, 谭建伟, 等. 柴油公交车行驶工况解析及排放特性研究[J]. 北京理工大学学报, 2010, 30(11): 1285-1289.
Liu Zhi-hua, Ge Yun-shan, Tan Jian-wei, et al. Analysis of bus driving cycle and investigation of bus emission characteristic[J]. Journal of Beijing Institute of Technology, 2010, 30(11): 1285-1289. [本文引用:1]
[6] Shi S, Lin N, Zhang Y, et al. Research on markov property analysis of driving cycles and its application[J]. Transportation Research Part D: Transport & Environment, 2016, 47: 171-181. [本文引用:2]
[7] Liu L, Huang C, Lu B, et al. Study on the design method of time-variant driving cycles for EV based on Markov process[C]∥Vehicle Power and Propulsion Conference (VPPC), IEEE, 2012: 1277-1281. [本文引用:2]
[8] Yue B, Shi S, Lin N, et al. Study on the design method of driving cycle with road grade based on Markov chain model[C]∥Vehicle Power and Propulsion Conference, IEEE, 2015: 1-5. [本文引用:1]
[9] 韦淑颖. 乘用车瞬态运行工况设计方法的改进研究[D]. 长春: 吉林大学交通学院, 2008.
Wei Shu-ying. Improvements of the design method of transient driving cycles for passenger car[D]. Changchun: College of Transportation, Jilin University, 2008. [本文引用:1]
[10] 石琴, 仇多洋, 周洁瑜. 基于组合聚类法的行驶工况构建与精度分析[J]. 汽车工程, 2012, 34(2): 164-169.
Shi Qin, Chou Duo-yang, Zhou Jie-yu. Driving cycle construction and accuracy analysis based on combined clustering technique[J]. Automotive Engineering, 2012, 34(2): 164-169. [本文引用:2]
[11] DieselNet. Emisson test cycle[EB/OL][2016-04-24]. https:∥www.dieselnet.com/standards/cycles/index.php. [本文引用:1]
[12] Lee T C, Judge G G, Zellner A. Estimating the parameters of the markov probability model from aggregate time series data[J]. Journal of the American Statistical Association, 1971, 66(335). [本文引用:1]
[13] Haveliwala T, Kamvar S. The second eigenvalue of the Google matrix[R]. San Francisco Bay Area: Stanford University, 2003. [本文引用:2]
[14] 孙洪祥. 随机过程[M]. 北京: 机械工业出版社, 2007. [本文引用:1]
[15] 苟江涛. 基于谷歌矩阵第二特征值重数的两类外推加速算法[D]. 北京: 清华大学数学科学系, 2009.
Gou Jiang-tao. The multiplicity of second eigenvalue of Google matrix and two new extrapolation methods[D]. Beijing: Department of Mathematical Sciences, Tsinghua Uuniversity, 2009. [本文引用:1]
[16] Haveliwala T, Kamvar S, Klein D, et al. Computing PageRank using power extrapolation[R]. San Francisco Bay Area: Stanford University, 2003. [本文引用:1]