特大城市居民出行方式选择行为的混合Logit模型

引用本文

栾鑫, 邓卫, 程琳, 陈新元. 特大城市居民出行方式选择行为的混合Logit模型[J].吉林大学学报（工学版）, 2018,48(4): 1029-1036
LUAN Xin, DENG Wei, CHENG Lin, CHEN Xin-yuan. Mixed Logit model for understanding travel mode choice behavior of megalopolitan residents[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 1029-1036 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170561
Permissions

特大城市居民出行方式选择行为的混合Logit模型

栾鑫¹, 邓卫¹, 程琳¹, 陈新元^2,³

1.东南大学交通学院, 南京 211189

2. 蒙纳士大学交通研究所, 墨尔本 VIC3168

3.蒙纳士大学土木工程系,墨尔本 VIC3168

通讯作者:程琳(1963-),男,教授,博士生导师.研究方向:交通运输规划与管理.E-mail:gist@seu.edu.cn

作者简介:栾鑫(1992-),男,博士研究生.研究方向:交通运输规划与管理.E-mail:xinluan@seu.edu.cn

基金:国家自然科学基金项目(51578150,51378119); 国家留学基金项目(201806090195).

摘要

为缓解交通供需冲突、改善居民出行结构模式,基于随机效用最大化理论,以特大城市南京为例,明确了影响出行方式选择行为的多重变量;通过建立混合logit(Mixed logit,ML)数理模型分析了家庭特征、个人属性、出行信息、居民出行OD位置4者的相互作用机理,并分析解读了ML模型输出的统计回归结果。研究结果表明:当时间要求性不高时,慢行方式的竞争性能得以凸显,但随着出行时间的增加,这种优势效用会逐步减弱;而在市郊、长距离行程中,公共交通(含地铁)或小汽车出行方式对旅客吸引力更大。

关键词: 交通运输系统工程; 出行方式选择; 混合Logit模型; 居民出行结构优化; 政策导向

中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2018)04-1029-08

Mixed Logit model for understanding travel mode choice behavior of megalopolitan residents

LUAN Xin¹, DENG Wei¹, CHENG Lin¹, CHEN Xin-yuan^2,³

1.School of Transportation, Southeast University, Nanjing 211189, China

2.The Institute of Transport Studies, Monash University, Melbourne VIC3168, Australia

3.Department of Civil Engineering, Monash University, Melbourne VIC3168, Australia

Abstract

In order to alleviate the conflicts of traffic supply and demand, improve the resident trip structure and mode, multiple variables impacting the travel mode choice were defined based on the random utility maximization theory with Nanjing City as a specific case. Mixed Logit (ML) model was established for analyzing and interpreting the influence and interaction mechanism of behavioral characteristics among household properties, individual attributes, trip information and the locations of trip ODs. The outcomes of ML model were analyzed by statistic regression. Results show that competitiveness of slow modes (non-motorized transport) become better if the time requirement is not high. However, with travel time increasing, the advantages op the slow modes are gradually weaken. Moreover, in suburbs and long distance trips, public transports (including metro) become more attractive to passengers. The results of statistic regression may help urban planners and transportation policy makers to integrate limited road resources systematically to ensure the resident travel comfortable, convenient and efficient.

Keyword: engineering of communications and transportation system; travel mode choice; mixed Logit model; structure optimization of residents' trips; policy orientation

文章图片

0 引言

广义上讲, 出行方式选择是一消费者选择行为, 符合消费者行为理论^[1]。离散选择模型(即多重变量分析)是处理上述问题的有效手段, 为国内外学者接受认可。以荷兰出行数据为例, Krygsman等^{[2, 3]}理解了微观个体、出行时间和居住地背景下的多模式出行, 认为其中步行和自行车是最主要交通方式, 其结论对多式联运换乘系统设计有指导意义; Limtanakool等^[4]探究了中长距离下的出行方式选择, 采用描述性统计及BL(Binary logit)建模方法, 估量了社会经济、土地利用、时间等变量在不同出行目的下对出行方式的影响, 结果表明土地利用和出行时间在模型中解释性更高; 此外, Abane等^[5]采用多项Logit(MNL)模型进行校准标定, 调查了加纳都市区居民通勤的方式选择特性响应状况, 多数对象更关注于出行费用及可达性; 根据雅典市中心实地考察, Papadimitriou等^[6]利用ML模型从道路交通、人为因素方面讨论了行人过街的行为特点。

国内学者也开展了大量应用研究, 陈坚等^[7]对Logit模型的效用函数部分进行优化, 构造了潜变量和显变量共同作用的SEM-Logit整合模型, 并用于实例印证出行者公交、非公交方式的选择问题; 叶茂等^[8]研究了扬州居民不同活动模式下的出行方式选择, 发现性别、年龄、小汽车或自行车有、无等因素有显著作用。ML模型能有效反映个体异质性、且对居民出行方式选择行为的解释程度更高, 但其相关研究却并不多见。以计划行为理论为基础, 景鹏等^[9]构建混合选择模型对通勤出行中的公交车和小汽车选择加以拟合, 而周伟等^[10]采用ML模型量化探索了出行者的路线选择行为, 认为个人年龄、收入等能产生较大影响。目前, ML模型在特大城市居民出行方式选择行为上的探讨略显不足, 尚缺乏系统化的论证分析。

综上所述, 作者考虑了多种出行方式(步行、非机动车、常规公交、地铁、小汽车等), 充分结合我国特大城市居民出行状况调查(原始数据), 采用理论与实践结合的手段, 通过MNL改进式— — ML模型从4方面16个变量对南京居民的出行方式选择特性展开了全面系统的阐释和量化应用, 提出了有利城市交通和居民出行的相关政策建议。

1 混合Logit模型

基于随机效用最大化的离散选择模型是行为选择研究中常用分析方法, 考虑到居民出行方式选择为典型无序多分类, MNL模型的应用最广泛, 其理论基础建立在不相关变量独立性(IIA)之上; 而ML模型, 又称随机参数Logit或Logit Kernel模型, 是一典型高度适应性模式, 假定待估参数向量服从一定分布形式, 体现出个体对出行方式选择的喜好随机性, 且不具有IIA特性带来的比值无关性缺陷^[11], 提高了模型预测精度和可靠性, 具有更丰富的物理意义。

1.1 数学结构表达

混合Logit模型是标准Logit的积分式, 每一分枝项均有特定阐述, 更清楚说明了其能标定任何模型, 选择概率表现为:

$P_{ni} = \int L_{ni} (β) f (β | θ) d β$ (1)

式中: $f (β | θ)$ 代表概率密度函数, 如正态、对数正态、均匀分布等; $L_{ni} (β)$ 是选择概率在参数 $β$ 上的评估界定:

$L_{ni} (β) = \frac{e^{V_{ni} (β)}}{\overset{J}{\sum_{j = 1}} e^{V_{nj} (β)q}}$ (2)

式中: $L_{ni} (β)$ 为效用可观测部分; $V_{ni} (β) = β' x_{ni}$ , 由此可知ML概率表达式为:

$P_{ni} = \int e^{β' x_{ni}} / \overset{J}{\sum_{j = 1}} e^{β' x_{nj}} f (β | θ) d β$ (3)

式(3)可视作Logit模型选择概率的加权平均值, 其权重由 $f (β | θ)$ 决定; $θ$ 为分布函数未知系数, 如正态分布的均值(M)、标准差(S)等。

1.2 数值仿真运算

对选择概率为隐性模型而言(向量 $β'$ 维数大于2时), 需先求其仿真解, 进而获取仿真极大似然函数, 再展开迭代推算^[12]。求解流程如下:

(1)计算仿真概率 $\overset{\lor}{P_{ni}},$ 以给定 $θ$ 值为前提进行有效估计。估计过程如下:① 从密度函数 $f (β | θ)$ 中随机提取某一向量 $β,$ 记作 $β^{r},$ 第一次抽取时令 $r = 1;$ ② 运算得 $L_{ni} (β^{r})$ 值; ③ 重复步骤①和②数次, 取 $L_{ni} (β^{r})$ 均值为其仿真概率:

$\overset{\lor}{P_{ni}} = \frac{1}{R} \overset{R}{\sum_{r = 1}} L_{ni} (β^{r})$ (4)

(2)构造极大似然算子。记样本量为 $N,$ 选择枝个数是 $I,$ 并定义辅助变量 $y_{ni} 。$

$y_{ni} = \{\begin{array}{l} 1, 个体 n 采用了选择肢 i \\ 0, 其他 \end{array}$ (5)

则仿真似然函数为:

$SL (β) = \overset{N}{\prod_{n = 1}} \overset{I}{\prod_{i = 1}} \overset{\lor}{P_{ni}^{y_{ni}}}$ (6)

对式(6)取对数即可得仿真极大似然算子:

$SLL (β) = \overset{N}{\sum_{n = 1}} \overset{I}{\sum_{i = 1}} y_{ni} \ln {\overset{\lor}{P}}_{ni}$ (7)

(3)求解 $θ 。$ 改变 $θ$ 值使式(7)取最大值, 可运用Newton-Rapson法、梯度法、BHHH法等, 本文采取了Newton-Rapson法。

2 研究方法设计

城市居民出行方式选择行为, 从本质上而言, 其重点研究对象是生活在城市中人的交通行为, 表达了个体微观层面的决策过程, 是城市交通模式和居民出行结构的微观体现, 而关联于出行方式选择行为的因素是多种多样、复杂的, 不但涉及出行者自身, 还受外界其他变量(社会、经济、交通设施等)影响, 其中主要囊括了城市特征、居民个体及家庭特性、出行性质、目的地区域特点等^{[5, 8, 13, 14]}; 因此, 有必要从个体角度对特大城市居民的出行方式选择行为进行深入研究。

考虑到前述居民出行方式选择影响要素的分析, 最后确定从家庭特征、个人属性、出行信息、起讫位置(OD)特点4个方面论述剖析特大城市的出行方式选择行为; 而相较其他3个影响因素, 居民出行OD位置元素往往不可直接获取, 因此在具体建模研究前, 需对其进行地理特征分类。

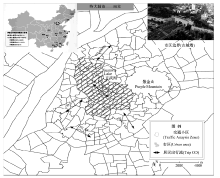
讨论居民出行OD位置性质时, 以南京古城墙为边界, 将其交通小区(TAZs)划分为位于市区(Urban area)和郊区(Suburb)两部分。如图1所示, 共有77个小区位于市区, 约占南京市交通小区总数(315个)的25%。基于此可将城市居民出行流向分成4类:郊区-郊区、郊区-市区、市区-郊区、市区-市区。

	Figure Option View Download New Window
	图1 南京市研究范围Fig.1 Survey region of Nanjing city

3 基础数据集

本文应用原始数据源自2014年南京市居民出行情况调研(包括问询、入户调查等), 其中只有行程时间是连续变量, 其余则均为离散分类型变量。基于构造定量模型的需要, 基于数据完整有效原则, 对数据体进行了筛选清洗和离散化处置。最后共选用了步行、非机动车、常规公交、地铁、小汽车和单位班车6种出行方式, 其他方式(如摩托车、出租车)由于样本量小等原因, 同时考虑到研究主体与侧重点, 所以未在建模中体现。

在数据初步处理、预建模过程中, 职业类别要素在各交通方式上均未通过显著性水平检验; 同样国外的发展经验也证实, 随着汽车工业化推进, 各种职业人们购买小汽车比例趋于平均化, 该因素对出行方式选择的影响也逐渐减弱^[15], 故在进一步量化分析中予以剔除。

在对调查数据集进行预处理后, 所需元素(虚拟变量, Dummy variables)共有4个层面:

(1)家庭特征:家庭成员数、学龄前儿童、外来人口、年收入、是否拥有小汽车和非机动车。

(2)个人属性:性别、年龄、是否为户主、持有驾照或公交卡与否、受教育程度。

(3)出行信息:目的、是否位于行程高峰、时间。

(4)出行OD位置— — 与市郊区联系; 计16个变量的11 815条出行数据被纳入到最终建模讨论中。

模型所采用的变量、符号标识、设置的参照变量(取值为0)及对应频数与百分比详见表1。

表1 带入变量的描述性统计说明 Table 1 Descriptive statistics of modeling variables

4 实例验证

4.1 ML模型估计结果

依据前述模型架构与变量声明及数据集的导入, 选取6种出行方式选择为自变量、其他变量为因变量, 从家庭属性、个体特征、出行信息、出行OD位置元素4个方向实现论证解析, 则表达南京居民出行方式选择行为特点的公式如下:

$\{\begin{array}{l} P_{ni} = \int e^{β' x_{ni}} / \overset{J}{\sum_{j = 1}} e^{β' x_{nj}} f (β | θ) d β \\ V_{ni} (β) = β' x_{ni} = f (H_{n}, I_{n}, T_{n}, L_{n}) \end{array}$ (8)

式中: $P_{ni}$ 为第 $n$ 个居民采取第 $i$ 种方式的概率; $V_{ni} (β)$ 是衡量个体选用第 $i$ 种交通方式的系统参数: $H_{n}$ 为家庭特征参量; $I_{n}$ 是个人变量参数; $T_{n}$ 为出行信息参量; $L_{n}$ 是出行者OD位置变量; 参考类别确定为单位班车方式。

预建模过程中, 作者进行了大量参数分布假设, 如对数正态、正态、均匀分布或其组合等, 但多数情况下, 模型运算结果无法收敛; 最终若考虑变量为连续变量, $f (β | θ)$ 服从正态分布; 变量为分类变量, $f (β | θ)$ 服从均匀分布时, 可取得收敛良好的多重变量回归结果, 见表2。

表2 城市居民出行方式选择行为分析的ML模型回归结果 Table 2 ML modeling regression analysis results of metropolitan residents’ travel mode choice behavior

	变量	步行		非机动车		常规公交		地铁		小汽车
	变量	Coeff.	p	Coeff.	p	Coeff.	p	Coeff.	p	Coeff.	p
	CONSTANT	7.899^{* * *}	△	0.762^{* *}	0.044	-1.558^{* * *}	△	-8.118^{* * *}	△	-2.334^{* * *}	0.002
家庭特征	MEMBER_M	/	/	-0.390^{* *}	0.017	/	/	/	/	/	/
	CHILD_M	0.955^{* *}	0.015	/	/	/	/	/	/	/	/
	MIGRANT_M	/	/	2.450^{* * *}	0.009	1.857^*	0.065	/	/	/	/
	INCOMEL_M	/	/	/	/	0.806^{* * *}	0.004	1.936^{* * *}	△	-0.745	0.105
	INCOMELM_M	-0.680^*	0.100	0.319^*	0.085	1.027^{* * *}	△	1.281^{* * *}	0.002	/	/
	INCOMEUM_M	/	/	0.273	0.120	0.702^{* * *}	△	1.270^{* * *}	0.001	/	/
	CAR_M	-2.196^{* * *}	△	-0.733^{* * *}	△	-0.525^{* * *}	0.005	/	/	4.863^{* * *}	△
	BIKE_M	-2.332^{* * *}	0.002	2.767^{* * *}	△	-0.592^{* *}	0.027	1.760^{* * *}	0.006	-0.633^*	0.090
个人属性	GENDER_M	2.179^{* * *}	△	0.727^{* * *}	△	0.623^{* * *}	△	1.026^{* * *}	△	0.389^*	0.085
	AGEY_M	1.553^{* *}	0.014	0.806^*	0.080	1.369^{* * *}	0.004	1.464^*	0.095	1.536^{* * *}	0.008
	AGEM_M	-3.296^{* * *}	△	0.359^{* * *}	0.009	0.480^{* * *}	0.002	1.006^{* * *}	0.003	0.307	0.106
	AGEO_M	4.183^{* * *}	△	/	/	1.234^{* * *}	△	1.329^{* *}	0.011	/	/
	CARD_M	0.973^{* * *}	0.003	/	/	1.419^{* * *}	△	1.624^{* * *}	△	-1.272^{* * *}	△
	HEAD_M	/	/	0.240^*	0.082	/	/	/	/	0.437^{* *}	0.027
	LICENSE_M	-1.169^{* * *}	△	-1.522^{* * *}	△	-1.230^{* * *}	△	-0.689^{* *}	0.017	1.678^{* * *}	△
	EDU_M	1.375^{* * *}	△	0.700^{* * *}	△	/	/	-0.487^*	0.090	/	/
	变量	步行		非机动车		常规公交		地铁		小汽车
	变量	Coeff.	p	Coeff.	p	Coeff.	p	Coeff.	p	Coeff.	p
出行信息	WORK_M	-4.109^{* * *}	△	-0.554^{* * *}	△	-0.473^{* * *}	0.001	/	/	-0.652^{* * *}	△
	SCHOOL_M	/	/	/	/	1.032^*	0.055	0.933	0.128	/	/
	SHOPPING_M	3.748^{* * *}	△	/	/	1.097^{* *}	0.020	/	/	-1.304^*	0.065
	LEISURE_M	5.089^{* * *}	△	1.111^{* *}	0.026	2.280^{* * *}	△	2.130^{* * *}	0.001	2.212^{* * *}	△
	PEAK_M	-0.532^*	0.078	0.565^{* * *}	△	/	/	0.669^{* * *}	0.004	/	/
	TTIME_M	-0.239^{* * *}	△	-0.065^{* * *}	△	0.021^{* * *}	△	0.042^{* * *}	△	0.059^{* * *}	△
	TTIME_S	0.138^{* * *}	△	0.029^{* * *}	△	0.033^{* * *}	△	0.013^{* * *}	0.009	0.015^{* * *}	△
出行OD位置	OD_UU_M	0.760^{* * *}	0.005	0.959^{* * *}	△	0.575^{* * *}	0.003	1.178^{* * *}	0.005	/	/
	OD_US_M	-4.129^{* * *}	△	-0.517^{* * *}	0.007	0.450^{* *}	0.022	2.588^{* * *}	△	1.296^{* * *}	0.003
	OD_SU_M	-4.884^{* * *}	△	-0.430^{* *}	0.026	0.393^{* *}	0.050	2.581^{* * *}	△	1.188^{* * *}	0.005
	模型统计汇总	样本量	11 815
Log Likelihood		-11 997
Likelihood Ratio		18 345
Aldrich-Nelson		0.608 3
Cragg-Uhler 1		0.788 3
Cragg-Uhler 2		0.810 8
Estrella		0.869 3
Adjusted Estrella		0.864 2
McFadden LRI		0.433 3

注:“ △ ” 代表p< 0.001; “ /” 代表p> 0.10; “ ^*” 代表p≤ 0.10; “ ^{* *}” 代表p≤ 0.05; “ ^{* * *}” 代表p≤ 0.01。

表2 城市居民出行方式选择行为分析的ML模型回归结果 Table 2 ML modeling regression analysis results of metropolitan residents’ travel mode choice behavior

4.2 结果分析

由表2可知, 行程时间的参数 $β$ 通过了分布函数显著性检验, 但鉴于篇幅所限, 有关变量的“ _S” 部分加以省略。其 $β$ 服从的分布情况为:

$\begin{array}{l} TTIM E_{步行} ~ N (- 0.239, 0 . 138^{2}), \\ TTIM E_{非机动车} ~ N (- 0.065, 0 . 029^{2}), \\ TTIM E_{公交车} ~ N (0.021, 0 . 033^{2}), \\ TTIM E_{地铁} ~ N (0.042, 0 . 013^{2}), \\ TTIM E_{小汽车} ~ N (0.059, 0 . 015^{2}) 。 \end{array}$

可以看出, ML模型体现出不同类型人对出行时间重要性认识的差异, 这与实际相符; 也表达了该模型能更合理解释居民个体的出行方式选择行为。

其中, 效用函数作说明如下(因部分公式同理可求, 在此不再重述, 仅列出前两种交通方式):V_n_步行=7.899+0.955CHILD-

0.680INCOMELM-2.196CAR-2.332BIKE+

2.179GENDER+1.553AGEY-3.296AGEM+

4.183AGEO+0.973CARD-1.169LICENSE+

1.375EDU-4.109WORK+3.748SHOPPING+

5.089LEISURE-0.532PEAK-0.239TTIME+

0.760OD_UU-4.129OD_US-4.884OD_SU

(9)

V_n_非机动车=0.762-0.390MEMBER+

2.450MIGRANT+0.319INCOMELM-

0.733CAR+2.767BIKE+0.727GENDER+

0.806AGEY+0.359AGEM+0.240HEAD-

1.522LICENSE+0.700EDU-0.554WORK+

1.111LEISURE+0.565PEAK-0.065TTIME+

0.959OD_UU-0.517OD_US-0.430OD_SU

(10)

综合考量模型统计回归结果可知:

(1)就慢行交通(步行与非机动车)而言, 家庭中有学龄前儿童、外来人口、女性、年龄偏小、学历较高者、休闲时更倾向于选择该方式; 居民在工作、市郊流向(时间相对紧迫)出行中的偏重性并不显著(Coeff.=-4.109^{* * *}、-0.554^{* * *}, -4.129^{* * *}、-0.517^{* * *}); 另外, 非机动车在高峰时段具备特定竞争力, 能满足不同群体多类行程要求(Coeff.=0.565^{* * *}), 但随着出行时间的增加, 与步行方式一样, 其优势会逐渐削弱; 而有非机动车的居民相较其他交通选择, 往往会采取非机动化或地铁方式(Coeff.=2.767^{* * *}、1.760^{* * *}), 说明这部分出行者会考虑选用该方式与之接驳。

(2)公共交通(包括地铁)层面, 低收入和中等收入家庭、中年人、年龄较小或偏大者、拥有市民卡的居民更偏向此种选择; 个体在工作出行中并不倾向于常规公交, 居民上学时却侧重采用公共交通(Coeff.=1.032^*), 这主要可能是由不同方式的时间可控性、要求性不同所造成; 同时在娱乐、长距离出行和随出行时耗增大时, 公共交通(尤其地铁方式)在长途行程需求上的竞争力明显占优(Coeff.=2.130^{* * *}、2.588^{* * *}、0.042^{* * *}), 行程越长对乘客吸引力愈强, 且在一定程度上能满足城区内部或短距离出行。

(3)拥有小客车、年轻人、男性、户主、持有驾照的居民会较显著采用小汽车方式出行, 低收入出行者却并不倾向(Coeff.=-0.745, p=0.105); 与工作、生活购物目的相比, 休闲娱乐和长途出行中该方式的选择侧重性更明显(Coeff.=2.212^{* * *}、1.296^{* * *})。当工作出行、高峰或市郊流向时, 单位班车的优点充分体现, 这说明班车在通勤行为中的效率更高。也可考虑分担部分小汽车客流至其他方式, 改善城市交通运行状态。

5 结论

(1)在市区内部, 应保障慢行交通路权(环境), 推广自行车公共租赁系统, 倡导“ 随用随骑、骑后速还” 理念, 鼓励非机动化的换乘方式出行, 提高短距离出行中的慢行交通比例, 形成绿色交通模式(基于变量BIKE、CARD); 减轻城市居民日常的通勤出行压力, 抑制小汽车出行、缓和目前交通拥堵状况。

(2)而城市外围或规律性拥挤主干道外侧以及大型公共交通枢纽附近宜考虑打造TOD模式社区, 中高密度规划、集约开发相关配套基础设施, 服务于中低收入人群, 缓解职住错位现象、避免“ 钟摆式” 交通, 减少平均出行时间或距离(对应变量WORK、SCHOOL、PEAK); 同时给城市公交系统带来可观客流量, 引导居民合乘(包括班车/校车), 特别在高峰时减轻交通负荷、以均衡交通需求时空分布。

(3)常规公交服务水平及运力尤需继续提升, 不应成为城市交通运输的短板, 而是和轨道交通系统交融在一起、协调共处(响应变量CAR、LICENSE), 同小汽车方式出行加以竞争; 且轨道交通建设应有序、有组织、有规模(分区域重点开发), 并做好与其他交通方式间的无缝衔接、换乘等工作。

(4)可选取其他不同优化改进的数学模型(如构造截断正态函数、S_B分布假定等)从新颖、多样化视角切入, 对居民出行的方式选择特性予以反映; 或考虑基于社会心理、行为学、复杂系统工程学、大数据等理论方法, 挖掘潜在影响要素和特质, 从而有效解决各类群体的交通出行问题。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Mcfadden D. Economic choices[J]. American Economic Review, 2001, 91(3): 351-378. [本文引用:1]
[2]	Krygsman S, Dijst M, Arentze T. Multimodal public transport: an analysis of travel time elements and the interconnectivity ratio[J]. Transport Policy, 2004, 11(3): 265-275. [本文引用:1]
[3]	Krygsman S, Arentze T, Timmermans H. Capturing tour mode and activity choice interdependencies: a co-evolutionary Logit modelling approach[J]. Transportation Research Part A: policy and Practice, 2007, 41(10): 913-933. [本文引用:1]
[4]	Limtanakool N, Dijst M, Schwanen T. The influence of socioeconomic characteristics, land use and travel time considerations on mode choice for medium-and longer-distance trips[J]. Journal of Transport Geography, 2006, 14(5): 327-341. [本文引用:1]
[5]	Abane A M. Travel behaviour in Ghana: empirical observations from four metropolitan areas[J]. Journal of Transport Geography, 2011, 19(2): 313-322. [本文引用:2]
[6]	Papadimitriou E, Lassarre S, Yannis G. Introducing human factors in pedestrian crossing behaviour models[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2016, 36: 69-82. [本文引用:1]
[7]	陈坚, 晏启鹏, 杨飞, 等. 出行方式选择行为的SEM-Logit整合模型[J]. 华南理工大学学报: 自然科学版, 2013, 41(2): 51-58. Chen Jian, Yan Qi-peng, Yang Fei, et al. SEM-Logit integration model of travel mode choice behaviors[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(2): 51-58. [本文引用:1]
[8]	叶茂, 于淼, 过秀成, 等. 历史城区居民出行活动模式选择影响因素分析[J]. 东南大学学报: 自然科学版, 2014, 44(1): 211-215. Ye Mao, Yu Miao, Guo Xiu-cheng, et al. Analysis of effects of contributing factors on choice of activity pattern in historic urban areas[J]. Journal of Southeast University(Natural Science Edition), 2014, 44(1): 211-215. [本文引用:2]
[9]	景鹏, 隽志才, 查奇芬. 考虑心理潜变量的出行方式选择行为模型[J]. 中国公路学报, 2014, 27(11): 84-92. Jing Peng, Juan Zhi-cai, Zha Qi-fen. Incorporating psychological latent variables into travel mode choice model[J]. China Journal of Highway and Transport, 2014, 27(11): 84-92. [本文引用:1]
[10]	周伟, 赵胜川. 基于Mixed Logit模型的路线选择行为量化分析[J]. 吉林大学学报: 工学版, 2013, 43(2): 304-309. Zhou Wei, Zhao Sheng-chuan. Quantitative analysis of traveler route choice behavior based on mixed Logit model[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(2): 304-309. [本文引用:1]
[11]	Hensher D A, Greene W H. The mixed Logit model: the state of practice and warnings for the unwary[J]. General Information, 2002, 30(2): 133-176. [本文引用:1]
[12]	Kattan L, Barros A G D, Saleemi H. Travel behavior changes and responses to advanced traveler information in prolonged and large-scale network disruptions: a case study of west LRT line construction in the city of calgary[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2013, 21(3): 90-102. [本文引用:1]
[13]	Martínez F, Aguila F, Hurtubia R. The constrained multinomial Logit: a semi-compensatory choice model[J]. Transportation Research Part B: Methodological, 2009, 43(3): 365-377. [本文引用:1]
[14]	Mcfadden D, Train K. Mixed MNL models for discrete response[J]. Journal of Applied Econometrics, 2000, 15(5): 447-470. [本文引用:1]
[15]	陈艳艳, 刘小明, 陈金川. 城市交通需求管理及应用[M]. 北京: 人民交通出版社, 2009: 152-192. [本文引用:1]

2001

0.0

... 0 引言广义上讲,出行方式选择是一消费者选择行为,符合消费者行为理论^[1] ...

2004

0.0

... 以荷兰出行数据为例,Krygsman等^[2,3]理解了微观个体、出行时间和居住地背景下的多模式出行,认为其中步行和自行车是最主要交通方式,其结论对多式联运换乘系统设计有指导意义 ...

2007

0.0

2006

0.0

... Limtanakool等^[4]探究了中长距离下的出行方式选择,采用描述性统计及BL(Binary logit)建模方法,估量了社会经济、土地利用、时间等变量在不同出行目的下对出行方式的影响,结果表明土地利用和出行时间在模型中解释性更高 ...

2011

0.0

... 此外,Abane等^[5]采用多项Logit(MNL)模型进行校准标定,调查了加纳都市区居民通勤的方式选择特性响应状况,多数对象更关注于出行费用及可达性 ...

... 2 研究方法设计城市居民出行方式选择行为,从本质上而言,其重点研究对象是生活在城市中人的交通行为,表达了个体微观层面的决策过程,是城市交通模式和居民出行结构的微观体现,而关联于出行方式选择行为的因素是多种多样、复杂的,不但涉及出行者自身,还受外界其他变量(社会、经济、交通设施等)影响,其中主要囊括了城市特征、居民个体及家庭特性、出行性质、目的地区域特点等^[5,8,13,14] ...

2016

0.0

... 根据雅典市中心实地考察,Papadimitriou等^[6]利用ML模型从道路交通、人为因素方面讨论了行人过街的行为特点 ...

2013

0.0

. 2013, 41(2):51-58 DOI:doi:10.3969/j.issn.1000-565X.2013.02.009

SEM-Logit integration model of travel mode choice behaviors

出行方式选择行为的SEM-Logit整合模型

Chen Jian , Yan Qi-peng , Yang Fei

陈坚, 晏启鹏, 杨飞

现有的出行方式选择行为模型仅考虑了可直接观测的出行者的个人社会经济特性和出行方案特性,并未考虑影响选择结果的潜变量,为此,文中提出了出行行为中潜变量的概念,并通过结构方程模型(SEM)刻画潜变量与显变量、潜变量与其测量变量之间的因果关系.然后,基于最大效用理论,对Logit模型的出行方式效用函数进行改进,构建了潜变量与显变量共同作用的SEM-Logit整合模型.结果表明:考虑了潜变量的整合模型的优度比传统Logit模型提高了0.201,最大似然函数估计值增加了20.607,证明潜变量对出行方式选择行为存在显著影响,所提出的整合模型的解释能力和精度较高.

... 国内学者也开展了大量应用研究,陈坚等^[7]对Logit模型的效用函数部分进行优化,构造了潜变量和显变量共同作用的SEM-Logit整合模型,并用于实例印证出行者公交、非公交方式的选择问题 ...

2014

0.0

. 2014, 44(1):211-215 DOI:doi:10.3969/j.issn.1001-0505.2014.01.038

Analysis of effects of contributing factors on choice of activity pattern in historic urban areas

历史城区居民出行活动模式选择影响因素分析

Ye Mao , Yu Miao , Guo Xiu-cheng

叶茂, 于淼, 过秀成

探讨了历史城区内居民出行活动模式选择的影响因素，依据扬州市历史城区居民调查数据，将居民出行活动划分为家工作/学习（内）家、家工作/学习（内）其他家、家工作/学习（外）家、家工作/学习（外）其他家和家其他家5种典型模式。采用多项Logit模型分析了5种活动模式的选择与居民个体及家庭属性之间的关系，并探索了不同活动模式下的出行方式选择情况。结果表明，个体出行者的性别、年龄、职业、有无小汽车和家庭电动自行车数量显著影响着出行活动模式的选择，而家庭人口数、有无学龄前儿童、家庭自行车数、有无摩托车及家庭收入对于历史城区居民出行活动模式选择的影响并不显著。

... 叶茂等^[8]研究了扬州居民不同活动模式下的出行方式选择,发现性别、年龄、小汽车或自行车有、无等因素有显著作用 ...

2014

0.0

. 2014, 27(11):84-92

Incorporating psychological latent variables into travel mode choice model

考虑心理潜变量的出行方式选择行为模型

Jing Peng , Juan Zhi-cai , Zha Qi-fen

景鹏, 隽志才, 查奇芬

... 以计划行为理论为基础,景鹏等^[9]构建混合选择模型对通勤出行中的公交车和小汽车选择加以拟合,而周伟等^[10]采用ML模型量化探索了出行者的路线选择行为,认为个人年龄、收入等能产生较大影响 ...

2013

0.0

. 2013, 43(2):304-309

Quantitative analysis of traveler route choice behavior based on mixed Logit model

基于Mixed Logit模型的路线选择行为量化分析

Zhou Wei , Zhao Sheng-chuan

周伟, 赵胜川

2002

0.0

... 而ML模型,又称随机参数Logit或Logit Kernel模型,是一典型高度适应性模式,假定待估参数向量服从一定分布形式,体现出个体对出行方式选择的喜好随机性,且不具有IIA特性带来的比值无关性缺陷^[11],提高了模型预测精度和可靠性,具有更丰富的物理意义 ...

2013

0.0

... 2 数值仿真运算对选择概率为隐性模型而言(向量 β'维数大于2时),需先求其仿真解,进而获取仿真极大似然函数,再展开迭代推算^[12] ...

2009

0.0

2000

0.0

2009

0.0

... 同样国外的发展经验也证实,随着汽车工业化推进,各种职业人们购买小汽车比例趋于平均化,该因素对出行方式选择的影响也逐渐减弱^[15],故在进一步量化分析中予以剔除 ...