基于惰性弯沉点的刚性下卧层深度设置方法

引用本文

臧国帅, 孙立军. 基于惰性弯沉点的刚性下卧层深度设置方法[J].吉林大学学报（工学版）, 2018,18(4): 1037-1044
ZANG Guo-shuai, SUN Li-jun. Method based on inertial point for setting depth to rigid layer[J]. Journal of Jilin University Engineering and Technology Edition, 2018,18(4): 1037-1044 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170679
Permissions

基于惰性弯沉点的刚性下卧层深度设置方法

臧国帅, 孙立军

同济大学道路与交通工程教育部重点实验室,上海 201804

通讯作者:孙立军(1963-),男,教授,博士.研究方向:道路与交通工程.E-mail:ljsun@tongji.edu.cn

作者简介:臧国帅(1992-),男,博士研究生.研究方向:沥青路面结构性能评价.E-mail:1310731@tongji.edu.cn

基金:国家自然科学基金项目(51678443).

摘要

针对目前刚性下卧层深度难以合理确定的问题,提出了一种新型的基于惰性弯沉点的设置方法——惰性点法。该方法通过在待评价路段内检测多条弯沉盆,利用均方根误差最小原则确定惰性弯沉点参数(位置和弯沉);基于惰性弯沉点不随上部结构层模量变化而变化的特性,使用粒子群优化算法迭代求解该路段的刚性层深度和土基模量。理论模拟分析表明,惰性点法可以精确反演刚性层深度,平均反演误差仅为1%。现场实测数据分析表明,沥青路面结构存在惰性点,并能用于刚性层深度和土基模量反演。与现有方法相比,惰性点法土基模量反演结果变异性较低,且能考虑地域差异。

关键词: 道路工程; 刚性下卧层; 惰性弯沉点; 模量反演; 粒子群算法; 弯沉盆

中图分类号:U416.2 文献标志码:A 文章编号:1671-5497(2018)04-1037-08

Method based on inertial point for setting depth to rigid layer

ZANG Guo-shuai, SUN Li-jun

Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China

Abstract

To solve the problem that it is difficult to reasonably determine depth of rigid layer, a novel method based on inertial point is proposed. First, the multiple deflection basin curves are detected within the section to be evaluated. Then, the parameters of inertial point (the offset distance and the deflection) are determined by obtaining the minimum of the root mean square error. Finally, the particle swarm optimization algorithm is applied to perform the iteration to back-calculate the rigid layer depth and subgrade modulus from the parameters of inertial point, whose deflection does not vary with the modulus of the upper layer. Analysis of theoretical simulation shows that the proposed method can accurately back-calculate the rigid layer depth with average back-calculation error of only 1%. The filed data show that the inertial point actually exists in the deflection basin curve measured on the asphalt pavement surface, and can be used to back-calculate the rigid layer depth and subgrade modulus. Compared with existing method, the variation of subgrade modulus back-calculated from the proposed method is lower, and the regional differences can be considered.

Keyword: road engineering; rigid layer; inertial point; modulus back-calculation; particle swarm optimization(PSO); deflection basin curve

文章图片

0 引言

刚性下卧层是指在线弹性层状体系模型中人为添加的刚性较大的结构层, 位于土基层下面一定深度处^[1]。刚性层的添加将模量反演计算限定在有限深度范围内, 减小了理论和实测弯沉盆匹配误差, 提高了模量反演结果合理性^{[2, 3, 4]}。然而, 刚性层深度往往难以合理确定。

Chou^[5]认为刚性层深度可通过反演法进行确定, 即将刚性层深度视作待反演的未知变量, 分别计算不同刚性层深度下的弯沉盆匹配误差, 则匹配误差达到最小时的刚性层深度即为实际刚性层深度。Rohde等^[6]通过实例分析发现弯沉盆匹配误差并不总是在实际刚性层深度时达到最小。刚性层深度也可通过定值法进行设置, 即在所有模量反演中均将刚性层深度设置为同一值, 如5.0 m^[7]、5.4 m^[8]、5.5 m^[9]、6.1 m^[10]。显然, 定值法不能考虑不同地区土基状况的差异。刚性层深度还可通过建立预估公式进行确定, 自变量可以为路面结构厚度^{[4, 11]}或弯沉零点位置^[6]等。

惰性弯沉点处弯沉不随上部结构层模量的变化而变化, 只与土基模量、刚性层深度和路面厚度有关^[12]。惰性弯沉点具有两个参数:惰性点位置和惰性点弯沉。对于实际路面结构, 路面厚度往往已知。当惰性弯沉点确定时, 则可以依据两个惰性点参数确定两个未知变量:土基模量和刚性层深度, 记此方法为惰性点法。

本文首先分析了惰性点法反演刚性层深度的理论精度, 随后进行了实例验证, 最后与反演法进行了对比分析, 表明惰性点法反演刚性层深度不仅具有可行性, 而且反演结果合理。

1 惰性点法反演原理

惰性弯沉点具有两个参数:惰性弯沉点至荷载中心距离( $R_{c}$ )和相应弯沉( $D_{c}$ )。惰性点参数只与路面总厚度(H)、土基模量( $E_{0}$ )、刚性层深度( $H_{rigid}$ )有关, 即:

$\{\begin{array}{l} R_{c} = f (H, E_{0}, H_{rigid}) \\ D_{c} = g (H, E_{0}, H_{rigid}) \end{array}$ (1)

路面总厚度(H)往往已知, 则式(1)简化为:

$\{\begin{array}{l} R_{c} = f (E_{0}, H_{rigid}) \\ D_{c} = g (E_{0}, H_{rigid}) \end{array}$ (2)

1.1 单点检测弯沉盆

对于单点检测弯沉盆, 根据既有经验或推荐值进行刚性层深度设置, 则式(2)简化为:

$\{\begin{array}{l} R_{c} = f (E_{0}) \\ D_{c} = g (E_{0}) \end{array}$ (3)

从式(3)可以看出, $R_{c}$ 和 $D_{c}$ 均是与 $E_{0}$ 具有一一对应关系的函数, 因此存在着如下的隐式函数关系:

$D_{c} = h (R_{c})$ (4)

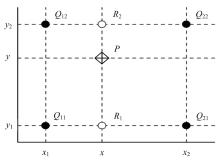
图1中曲线②是式(4)的轨迹, 当 $E_{0}$ 增大时, $R_{c}$ 和 $D_{c}$ 均减小, 轨迹指向荷载中心点; 曲线①是弯沉盆曲线。由于曲线①和②成一定角度, 只有一个交点, 即弯沉盆曲线上满足式(4)的点只有一个。这可以从直观上解释惰性点法反演土基模量具有唯一解^[13]。当已知曲线①和②时, 利用两条曲线间的弯沉差绝对值是土基模量 $E_{0}$ 的单峰函数的特性, 可基于0.618法求解土基模量。

	Figure Option View Download New Window
	图1 惰性点唯一性示意图Fig.1 Trajectory of inertial point and shape of deflection basin

1.2 路段检测多个弯沉盆

惰性点的确定需要保持土基模量和刚性层深度不变, 变化上部结构层模量, 得到多组弯沉盆曲线, 计算各径向距离的均方根误差RMSE(见式5), 则RMSE最小处即为惰性点^[14]。

$RMS E_{d} =$ $\sqrt{\frac{1}{n}\sum\limits{i=1}^{n}(\frac{w_{d}^{i}-\bar{w}^{d}}{\bar{w}^{d}})^{2}}$(5)

式中: $ε$ 为惰性点参数匹配误差; ${\hat{R}}_{c} 、 R_{c}$ 分别为惰性点位置的计算值和实测值; ${\hat{D}}_{c} 、 D_{c}$ 分别为惰性点弯沉的计算值和实测值。

对于某一较短路段, 路段内土基模量和刚性层深度可认为保持不变, 而面层和基层模量由于荷载和环境的耦合作用具有较大的空间变异性。因此, 可在路段内不同位置分别检测弯沉盆, 进而确定该待评价路段的惰性点参数 $R_{c}$ 和 $D_{c} 。$ 将惰性点参数代入式(2), 即可依据两个等式确定两个未知数:土基模量和刚性层深度。

式中: $n$ 为路面结构组合数; $w_{i}^{d}$ 为第 $i$ 组路面结构在径向距离为 $d$ 处的路表弯沉; ${\bar{w}}^{d}$ 为各组路面结构在在径向距离为 $d$ 处的路表弯沉平均值, ${\bar{w}}^{d}$ = $\overset{n}{\sum_{i = 1}} w_{i}^{d}$ /n。

1.2.1 反演算法

惰性点法待反演未知量为两个:土基模量和刚性层深度, 可采用迭代方法进行求解, 如粒子群优化(Particle swarm optimization, PSO)算法。目标函数定义为惰性点参数的相对均方根误差, 如式(6)所示:

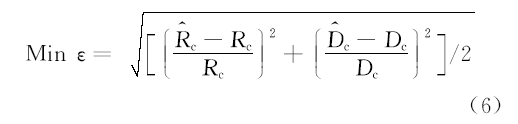
1.2.2 粒子群优化算法

粒子群优化算法具有容易理解、易于实现等突出优点, 在许多优化问题中得到成功应用。在PSO算法中每个粒子均为解空间中的一个点。如果粒子的种群大小为 $N,$ 第 $i (i = 1, 2, \dots, N)$ 个粒子位置表示为 $X_{i},$ 该粒子所经历过的个体历史最优值为 $p_{best}^{i},$ 速度用 $V_{i}$ 表示, 种群历史最优值为 $p_{best}^{g},$ 则粒子 $i$ 将根据式(7)(8)来更新自己的速度和位置^[15]:

$\begin{array}{l} V_{i} = ω V_{i} + c_{1} r_{1} (p_{best}^{i} - X_{i}) + c_{2} r_{2} (p_{best}^{g} - X_{i}) \end{array}$ (7)

$X_{i} = X_{i} + V_{i}$ (8)

式中: $c_{1} 、 c_{2}$ 为常数; $r_{1} 、 r_{2}$ 为[0, 1]上的随机数; $ω$ 为惯性权重(Inertia weight)。

式(7)由3部分组成, 第1部分为粒子先前的速度, 说明了粒子目前的状态; 第2部分为认知部分(Cognition modal), 表示粒子本身的思考; 第3部分为社会部分(Social modal), 表示了粒子间的信息共享。

2 惰性点法反演模型的建立

惰性点参数是路面结构厚度、土基模量和刚性层深度的函数。刚性层深度是指刚性下卧层与土基顶面之间的距离。对于某一待评价道路, 路面结构厚度已知, 因此仅需要计算不同土基模量和刚性层深度组合下的惰性点参数。为了计算各点的理论惰性点参数, 首先对土基模量和刚性层深度进行网格化处理, 计算各网格点对应的惰性点参数; 然后利用双线性插值(Bilinear interpolation)方法得到非网格点的惰性点参数。具体结果如下:刚性层模量取值为6894 MPa(1000 ksi), 泊松比取值为0.2^[4]。

2.1 网格化数据库生成

本文面向江西某高速公路进行沥青路面结构的性能评价, 其路面结构厚度为74 cm, 具体路面结构信息如表1所示, 其中AK16为抗滑表层, 详见《公路沥青路面施工技术规范》(JTJ032-94), 水泥稳定砂砾的水泥含量为4%。

表1 路面结构参数 Table 1 Pavement structure parameters

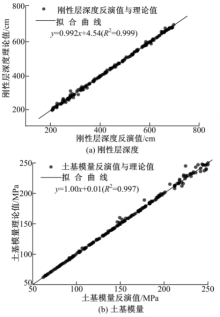
为了建立适用范围较广的网格化数据库, 将土基模量和刚性层深度网格化为101× 101的网格, 其中土基模量为50~350 MPa, 取样间隔为3 MPa; 刚性层深度为100~800 cm, 取样间隔为7 cm。共得到10 201个惰性点参数, 惰性点参数与土基模量和刚性层深度的散点图如图2所示。

	Figure Option View Download New Window
	图2 惰性点参数与土基模量和刚性层深度的散点图Fig.2 Scattered plots of parameters of inertial point and subgrade modulus and rigid layer depth

2.2 双线性插值方法

基于已建立的惰性点参数数据库, 采用双线性插值的方法得到其他土基模量和刚性层深度组合下的惰性点参数。假设已知函数 $H$ 在4个点 $Q_{11} 、 Q_{12} 、 Q_{21} 、 Q_{22}$ 处的函数值, 这4个点的坐标分别为 $(x_{1}, y_{1}) 、 (x_{1}, y_{2}) 、 (x_{2}, y_{1}) 、 (x_{2}, y_{2})$ 4个点的函数值, 求坐标为 $(x, y)$ 的点 $P$ 处的函数值, 如图3所示。

	Figure Option View Download New Window
	图3 双线性插值原理示意图Fig.3 Schematic diagram of bilinear interpolation method

首先, 在 $x$ 方向进行线性插值, 得到坐标为 $(x, y_{1})$ 的点 $R_{1}$ 和坐标为 $(x, y_{2})$ 的点 $R_{2}$ 处的函数值, 即:

$\begin{array}{l} H (R_{1}) \approx \frac{x_{2} - x}{x_{2} - x_{1}} H (Q_{11}) + \frac{x - x_{1}}{x_{2} - x_{1}} H (Q_{21}) \end{array}$ (9)

$H (R_{2}) \approx \frac{x_{2} - x}{x_{2} - x_{1}} H (Q_{12}) + \frac{x - x_{1}}{x_{2} - x_{1}} H (Q_{22})$ (10)

然后, 在 $y$ 方向进行线性插值, 得到:

$H (P) \approx \frac{y_{2} - y}{y_{2} - y_{1}} H (R_{1}) + \frac{y - y_{1}}{y_{2} - y_{1}} H (R_{2})$ (11)

3 惰性点法反演刚性层深度的理论精度分析

为了分析惰性点法的理论反演精度, 均匀随机生成200组土基模量和刚性层深度组合, 计算每个组合下的惰性点参数, 然后反演刚性层深度, 对比刚性层深度理论值与反演值。根据以往反算经验, 选取路面常见结构参数取值, 其中, 土基模量取值为60~250 MPa, 刚性层深度取值为200~700 cm。

反演结果如图4所示, 从中可以看出, 刚性层深度和土基模量的反演值与理论值非常接近, 相关系数 $R^{2}$ 分别为0.999和0.997。刚性层深度的平均反演误差为1.0%, 标准误差为6.0 cm; 土基模量的平均反演误差和标准误差分别为0.7%和2.85 MPa。这些指标均表明惰性点法反演刚性层深度和土基模量具有很高的理论精度。

	Figure Option View Download New Window
	图4 惰性点法反演值与理论值对比分析Fig.4 Comparison between back-calculated value based on inertial point and theoretical value

4 现场实例验证

4.1 现场实测弯沉盆

依托江西某高速公路改扩建工程, 检测沥青路面表面弯沉盆。在长度为600 m的范围内, 检测了60个弯沉盆。检测长度较短是为了保证评价区域内的土基模量和刚性层深度状况比较一致。为了准确确定惰性点参数, 检测弯沉盆应当具有较大差异, 即面层模量和基层模量应当具有较大差异, 因此选择路表不同损坏状况处检测路表弯沉盆。当路表具有破损时, 检测弯沉盆可能出现异常, 依据弯沉应当随着径向距离的增加而减小的变化趋势进行异常弯沉盆筛选。最终, 得到40组有效弯沉盆。

4.2 惰性点参数计算

落锤式弯沉仪(FWD)有9个弯沉传感器, 其径向分布如表2所示。惰性点参数的计算需已知每个测点的完整弯沉盆信息, 因此需要依据实测的9点弯沉预测完整弯沉盆信息。本文采取插值与拟合相结合的方法进行完整弯沉盆预测, 即采用对数线性插值预测FWD检测范围内的弯沉, 采用指数拟合方程预测FWD检测范围外的弯沉。拟合方法并不经过已知点, 而插值方法经过已知点。为了保证弯沉盆连续, 对拟合函数值按照式(12)进行修正, 使得其经过最外侧观测点w₉。

表2 FWD传感器径向位置及实测平均弯沉 Table 2 Radial distance of FWD sensors and corresponding measured average deflection

弯沉传感器	径向距离/mm	弯沉/mm
$w_{1}$	0	0.160
$w_{2}$	203	0.110
$w_{3}$	305	0.0947
$w_{4}$	457	0.0818
$w_{5}$	610	0.0708
$w_{6}$	914	0.0536
$w_{7}$	1219	0.0435
$w_{8}$	1524	0.0345
$w_{9}$	1829	0.0290

表2 FWD传感器径向位置及实测平均弯沉 Table 2 Radial distance of FWD sensors and corresponding measured average deflection

${\hat{w}}_{cor} = \hat{w} \times \frac{w_{9}}{{\hat{w}}_{9}}$ (12)

式中: $\hat{w}$ 为弯沉拟合值; ${\hat{w}}_{9} 、 w_{9}$ 分别为最大径向距离处弯沉拟合值和实测值; ${\hat{w}}_{cor}$ 为弯沉拟合修正值。

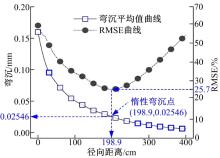
依据各测点的完整弯沉盆曲线, 计算各个径向距离处的弯沉平均值和均方根误差RMSE, 如图5所示。从图5可以看出, RMSE随着径向距离的增加呈现先降低后增加的变化趋势, 在 $R_{c} = 198.9 cm$ 处, RMSE达到极小值25.7%。根据RMSE最小原则, 此点即为惰性弯沉点, 表明沥青路面结构实际存在惰性弯沉点。惰性点处弯沉D_c=0.025 46 mm。

	Figure Option View Download New Window
	图5 RMSE及实测平均弯沉随径向距离的变化关系Fig.5 RMSE and measured average deflection vs radial distance

惰性点位置的RMSE较大, 可能是由于惰性点位于198.9 cm处, 处于FWD检测范围182.9 cm以外。FWD检测范围以外采用指数拟合方法进行弯沉盆信息外延预测, 而外延预测往往比较困难。此外, FWD检测误差和路表损坏均会引起检测弯沉盆异常, 可能也是RMSE较大的部分原因。

4.3 刚性层深度反演分析

第4.2节确定了该评价路段的惰性点参数为:

$\{\begin{array}{l} R_{c} = 198.9 cm \\ D_{c} = 0.02546 mm \end{array}$ (13)

基于此惰性点参数, 利用粒子群优化算法反演刚性层深度和土基模量, 得到:

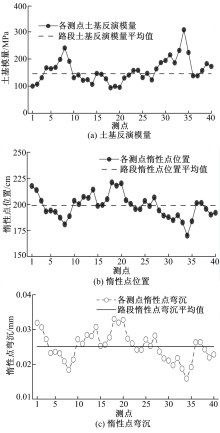
$\{\begin{array}{l} H_{rigid} = 377.9 cm \\ E_{0} = 145.6 MPa \end{array}$ (14)

惰性点法反演刚性层深度和土基模量的前提是评价路段内土基状况较为一致。为了验证土基状况是否一致, 分别计算各个测点在刚性层深度为377.9 cm下的土基模量反演值以及惰性点参数, 计算结果如图6所示, 统计分析结果如表3所示。从图6中可以看出, 各测点的惰性点参数较为接近, 而土基模量变化稍大, 总体仍能满足一致性要求。土基模量主要由FWD弯沉盆曲线外侧弯沉确定, 而外侧弯沉值较小, 使得测量误差影响较大, 造成土基反演模量变化稍大。

表3 路段内各测点土基模量及惰性点参数统计 Table 3 Statistics of subgrade modulus and parameters of inertial point at each measuring point within section

	Figure Option View Download New Window
	图6 路段总体和各测点的土基反演模量及惰性点参数对比Fig.6 Comparison of back-calculated subgrade modulus and parameters of inertial point between average of section and individual measuring point

5 不同刚性层深度确定方法对比

5.1 反演法确定刚性层深度

刚性层深度也可以通过反演法^[5]进行确定, 即将刚性层深度视作待反演的未知变量, 在不同刚性层深度下进行结构层模量反演, 计算目标函数值, 目标函数最小值对应的刚性层深度被认为是实际刚性层深度。采用反演法确定各测点的刚性层深度和土基模量, 并与惰性点法进行对比。鉴于刚性层深度过浅或过深均不具有实际意义, 反演法分析时将刚性层深度限制为200~700 cm。

5.2 两种方法对比分析

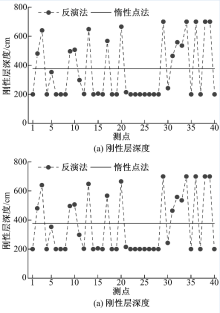
惰性点法和反演法的分析结果如图7和表4所示。从图7中可以看出, 各测点依据反演法确定的刚性层深度呈现两极分化趋势, 较多集中在200 cm, 部分为700 cm, 表明反演法具有一定的局限性。对于土基模量, 基于反演法确定的土基模量的变异性显著高于惰性点法, 这是由于惰性点法基于各测点弯沉盆, 综合确定出路段的刚性层深度, 各测点采用同一刚性层深度进行土基模量反演, 而反演法根据每个测点的弯沉盆分别确定刚性层深度, 进而确定土基模量。

	Figure Option View Download New Window
	图7 不同方法的反演值对比分析Fig.7 Comparison of back-calculated value between different methods

表4 不同方法反演值统计分析 Table 4 Comparison of statistic values between different methods

综上所述, 虽然反演法可以基于各测点弯沉盆分别确定刚性层深度, 但是刚性层深度变异性较大, 使得土基模量变异性较大; 惰性点法综合考虑评价路段内的所有弯沉盆信息确定刚性层深度, 使得路段采用同一刚性层深度, 显著降低了土基模量变异性。此外, 与定值法相比, 惰性点法可针对各个评价单元分别进行刚性层深度和土基模量反演, 并可考虑地域差异性。

6 结论

(1)惰性点法可以同时精确反演刚性层深度和土基模量, 理论平均反演误差分别为1%和0.7%。

(2)现场实测江西某高速公路改扩建工程沥青路面的多个弯沉盆, 基于均方根误差RMSE最小原则, 表明该沥青路面结构存在惰性弯沉点。基于此惰性点参数确定该路段的刚性层深度为377.9 cm, 土基模量为145.6 MPa。

(3)与既有方法相比, 惰性点法综合考虑路段内所有弯沉盆信息确定刚性层统一设置深度, 保证了土基反演模量的一致性, 且能考虑地域差异性。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	朱洁. 沥青路面多层结构模量高精度反算方法研究[D]. 上海: 同济大学交通运输工程学院, 2013. Zhu Jie. Method of the back-calculation of high-precision modulus for multilayer structures of asphalt pavement[D]. Shanghai: College of Transportation Engineering, Tongji University, 2013. [本文引用:1]
[2]	陈靖翔. 落重挠度仪检测荷重与坚硬层深度对反算分析之影响[D]. 台北: 国立台湾大学, 2006. Chen Jing-xiang. Load of the influence of FWD and hard layer depth on back-calculation[D]. Taibei: National Taiwan University, 2006. [本文引用:1]
[3]	谢兆星, 丛林, 郭忠印. 基于FWD弯沉盆参数的沥青路面土基模量评价方法研究[J]. 公路交通科技. 2009, 26(12): 28-31. Xie Zhao-xing, Cong Lin, Guo Zhong-yin. Evaluation of subsoil modulus for asphalt pavement based on FWD deflection basin parameter[J]. Journal of Highway and Transportation Research and Development, 2009, 26(12): 28-31. [本文引用:1]
[4]	余欢, 陈长. 沥青路面模量反演分析中刚性下卧层设置方法[J]. 交通科学与工程, 2014, 30(4): 1-6. Yu Huan, Chen Zhang. Setting method of rigid substratum in modulus back-calculation of the asphalt pavement[J]. Journal of Transport Science and Engineering, 2014, 30(4): 1-6. [本文引用:3]
[5]	Chou Y. Development of an expert system for nondestructive pavement structural evaluation[D]. Texas: Texas A&M University, 1989. [本文引用:2]
[6]	Rohde G T, Smith R E. Determining depth to apparent stiff layer from FWD data [R]. Texas: Texas Transportation Institute(FHWA/TX-91-1159-1), 1991. [本文引用:2]
[7]	Uzan J, Lytton R L, Germann F P. General procedure for backcalculating layer moduli[C]∥The 1st Conference on Nondestructive Testing of Pavements and Backcalculation of Moduli, West Conshohocken, PA, 1989: 217-228. [本文引用:1]
[8]	Yusuf Mehta, Roque Reynaldo. Evaluation of FWD data for determination of layer moduli of pavements[J]. Journal of Materials in Civil Engineering, 2003, 15(1): 25-31. [本文引用:1]
[9]	余欢. 沥青路面半刚性基层损坏评价及刚性下卧层深度设置[D]. 上海: 同济大学交通运输工程学院, 2015. Yu Huan. Damage evaluation of semi-rigid base and setting method of rigid substratum depth for asphalt pavement[D]. Shanghai: College of Transportation Engineering, Tongji University, 2015. [本文引用:1]
[10]	Bush III A J. Nondestructive testing for light aircraft pavements phase II development of the nondestructive evaluation methodology[R]. Washington: Army Engineer Waterways Experiment Station Geotechnical Lab(FAA-RD-80-9-II), 1980. [本文引用:1]
[11]	严菁. 沥青路面反演分析中刚性下卧层设置规律研究及应用[D]. 上海: 同济大学交通运输工程学院, 2010. Yan Jing. Research on the rule of setting the rigid bottom layer and its application in back-calculation of asphalt pavements [D]. Shanghai: College, Transportation Engineering, Tongji University, 2010. [本文引用:1]
[12]	孙立军, 八谷好高, 姚祖康. 水泥混凝土路面板模量反算的一种新方法——惰性弯沉法[J]. 土木工程学报, 2000, 33(1): 83-87. Sun Li-jun, Ba-Gu Hao-gao, Yao Zu-kang. A new method to backcalculate layer moduli for concrete pavements[J]. China Civil Engineering Journal, 2000, 33(1): 83-87. [本文引用:1]
[13]	Zhang Xiao-ning, Sun Li-jun. Novel method for backcalculation of asphalt pavement moduli[J]. Transportation Research Record, 2004, 1869: 67-72. [本文引用:1]
[14]	朱洁, 陈长, 孙立军. 沥青路面惰性弯沉点的选取及土基模量的反演[J]. 同济大学学报: 自然科学版, 2013, 41(12): 1824-1829. Zhu Jie, Chen Zhang, Sun Li-jun. Selection of inertial point for asphalt pavement and backcalculation method of subgrade modulus[J]. Journal of Tongji University (Natural Science), 2013, 41(12): 1824-1829. [本文引用:1]
[15]	张利彪, 周春光, 马铭, 等. 基于粒子群算法求解多目标优化问题[J]. 计算机研究与发展, 2004, 41(7): 1286-1291. Zhang Li-biao, Zhou Chun-guang, Ma Ming, et al. Solutions of multi-objective optimization problems based on particle swarm optimization[J]. Journal of Computer Research and Development, 2004, 41(7): 1286-1291. [本文引用:1]

2013

0.0

. 2013, :-

Method of the back-calculation of high-precision modulus for multilayer structures of asphalt pavement

沥青路面多层结构模量高精度反算方法研究

Zhu Jie

朱洁

... 0 引言刚性下卧层是指在线弹性层状体系模型中人为添加的刚性较大的结构层,位于土基层下面一定深度处^[1] ...

2006

0.0

... 刚性层的添加将模量反演计算限定在有限深度范围内,减小了理论和实测弯沉盆匹配误差,提高了模量反演结果合理性^[2,3,4] ...

2009

0.0

. 2009, 26(12):28-31 DOI:doi:10.3969/j.issn.1002-0268.2009.12.006

Evaluation of subsoil modulus for asphalt pavement based on FWD deflection basin parameter

基于FWD弯沉盆参数的沥青路面土基模量评价方法研究

Xie Zhao-xing , Cong Lin , Guo Zhong-yin

谢兆星, 丛林, 郭忠印

The asphalt pavement deflection basin response was simulated with FWD by dynamic FEM model. The relationship of subsoil modulus with deflection basin parameters was analyzed. Furthermore, the effects of structure cracks, layer interface sliding and depth of rigid layer on deflection basin response were investigated. The results show that (1) the curvature index CI_7 and shape factor F_8 can be used to determine the subsoil modulus; (2) crack and interface sliding have no influence on CI_7-F_8 characteristic curve; (3) the depth of rigid layer has impact on CI_7-F_8 characteristic curve when the depth is lower than 7 m. The method of subsoil condition assessment was verified by FWD measurements from test sections.

采用动力有限元方法模拟沥青路面在FWD作用下弯沉盆响应,分析土基模量与弯沉盆几何指标之间的关系以及路面开裂、层间滑移和刚性层深度等变量对弯沉盆的影响。计算结果表明:土基模量可由曲率指标CI7和形状指标F8确定;开裂和层间滑移对CI7-F8关系曲线没有影响;当刚性层深度小于7 m时,刚性层深度将对CI7-F8关系曲线产生影响。最后通过实体工程对评价方法进行了验证。

... 刚性层的添加将模量反演计算限定在有限深度范围内,减小了理论和实测弯沉盆匹配误差,提高了模量反演结果合理性^[2,3,4] ...

2014

0.0

. 2014, 30(4):1-6 DOI:doi:10.3969/j.issn.1674-599X.2014.04.001

Setting method of rigid substratum in modulus back-calculation of the asphalt pavement

沥青路面模量反演分析中刚性下卧层设置方法

Yu Huan , Chen Zhang

余欢, 陈长

摘　要：基于线弹性层状体系理论的反算程序，引入刚性下卧层，对理论弯沉盆与实际弯沉盆不匹配的问题进行了优化。选取不同的路面结构，借助有限元软件，考察了刚性下卧层的模量和设置深度对理论弯沉盆的影响，得到其合理的模量范围。以理论与实际弯沉盆各检测点弯沉差值平方和为误差指标，分析回归出刚性下卧层最佳设置深度与路面结构总厚度的关系。选取不同厚度的路面结构进行土基模量反演，证明了该刚性下卧层设置方法的可靠性。

... 刚性层的添加将模量反演计算限定在有限深度范围内,减小了理论和实测弯沉盆匹配误差,提高了模量反演结果合理性^[2,3,4] ...

... 刚性层深度还可通过建立预估公式进行确定,自变量可以为路面结构厚度^[4,11]或弯沉零点位置^[6]等 ...

... 2^[4] ...

1989

0.0

... Chou^[5]认为刚性层深度可通过反演法进行确定,即将刚性层深度视作待反演的未知变量,分别计算不同刚性层深度下的弯沉盆匹配误差,则匹配误差达到最小时的刚性层深度即为实际刚性层深度 ...

... 1 反演法确定刚性层深度刚性层深度也可以通过反演法^[5]进行确定,即将刚性层深度视作待反演的未知变量,在不同刚性层深度下进行结构层模量反演,计算目标函数值,目标函数最小值对应的刚性层深度被认为是实际刚性层深度 ...

0.0

... Rohde等^[6]通过实例分析发现弯沉盆匹配误差并不总是在实际刚性层深度时达到最小 ...

... 刚性层深度还可通过建立预估公式进行确定,自变量可以为路面结构厚度^[4,11]或弯沉零点位置^[6]等 ...

1989

0.0

... 0 m^[7]、5 ...

2003

0.0

... 4 m^[8]、5 ...

2015

0.0

. 2015, :-

Damage evaluation of semi-rigid base and setting method of rigid substratum depth for asphalt pavement

沥青路面半刚性基层损坏评价及刚性下卧层深度设置

Yu Huan

余欢

... 5 m^[9]、6 ...

0.0

... 1 m^[10] ...

2010

0.0

. 2010, :-

Research on the rule of setting the rigid bottom layer and its application in back-calculation of asphalt pavements [D]. Shanghai: College, Transportation Engineering,

沥青路面反演分析中刚性下卧层设置规律研究及应用

Yan Jing

严菁

... 刚性层深度还可通过建立预估公式进行确定,自变量可以为路面结构厚度^[4,11]或弯沉零点位置^[6]等 ...

2000

0.0

... 惰性弯沉点处弯沉不随上部结构层模量的变化而变化,只与土基模量、刚性层深度和路面厚度有关^[12] ...

2004

0.0

... 这可以从直观上解释惰性点法反演土基模量具有唯一解^[13] ...

2013

0.0

. 2013, 41(12):1824-1829 DOI:doi:10.3969/j.issn.0253-374x.2013.12.010

Selection of inertial point for asphalt pavement and backcalculation method of subgrade modulus

沥青路面惰性弯沉点的选取及土基模量的反演

Zhu Jie , Chen Zhang , Sun Li-jun

朱洁, 陈长, 孙立军

It is realized that there exists a point called the inertial point in the pavement deflection basin whose deflection does not vary with the modulus of the upper layer, provided that the subgrade modulus and the upper layer thickness remain unchanged in cement concrete pavement. In order to make the theoretical deflection basin and measured deflection basin match each, the writer of this paper takes the rigid substratum into the calculation of theoretical deflection basin. As a result of a significant amount of calculation, the writer found it’s very difficult to get inertial point in asphalt pavement structure. Since that, the writer developes a new method of selecting inertial point based on smallest criterion of root mean square error and applies it to the back calculation of the subgrade modulus. It is found that the value of base modulus contributes more to the precision of subgrade modulus backcalculation and the writer draws a conclusion about the relationship between the inertial point parameters and the structure information on both flexible base and semi rigid base. The writer demonstrates the precision of the induction formula theoretically through the back calculations in different pavement structures, the precision and the reliablility of subgrade modulus backcalculation method based on inertial point using measured deflection basin are verified by a comparative study of the backcalculation programs at home and abroad.

水泥混凝土路面存在弯沉几乎不随模量变化而变化的惰性弯沉点，并可用于反算水泥混凝土路面结构模量.为了使理论弯沉盆与实测弯沉盆相匹配，将刚性下卧层引入到理论弯沉盆的计算当中，经过大量的弯沉盆计算发现，沥青路面惰性弯沉点的选取较为困难，为此提出了一种基于均方根误差最小准则的惰性弯沉点选取方法，并将其应用于土基模量的反演中.在基于惰性弯沉点的土基模量反算中发现基层模量的大小对土基模量反演的精度有比较大的影响，并分别回归出针对柔性基层和半刚性基层的路面结构信息与惰性点参数的关系.选取不同的路面结构进行土基模量反演，理论上论证回归公式的精度，用实测弯沉盆进行模量反算，并与国内外其他反算程序比较，验证了基于惰性弯沉点的土基模量反演方法的精度和可靠性.

... 2 路段检测多个弯沉盆惰性点的确定需要保持土基模量和刚性层深度不变,变化上部结构层模量,得到多组弯沉盆曲线,计算各径向距离的均方根误差RMSE(见式5),则RMSE最小处即为惰性点^[14] ...

2004

0.0

. 2004, 41(7):1286-1291

Solutions of multi-objective optimization problems based on particle swarm optimization

基于粒子群算法求解多目标优化问题

Zhang Li-biao , Zhou Chun-guang , Ma Ming

张利彪, 周春光, 马铭

... 如果粒子的种群大小为 N,第 i(i=1,2,…,N)个粒子位置表示为 Xi,该粒子所经历过的个体历史最优值为 pbesti,速度用 Vi表示,种群历史最优值为 pbestg,则粒子 i将根据式(7)(8)来更新自己的速度和位置^[15]: ...