作者简介:王继新(1975-),男,教授,博士生导师.研究方向:混合动力工程机械.E-mail:jxwang@jlu.edu.cn
针对工程机械作业载荷分布估计的问题,基于AIC准则及 K-means算法,提出了一种载荷分段混合分布估计方法。根据Luise分组方法,得到正态分布、对数正态分布及威布尔分布的卡方检验值。选取最小卡方检验值对应的分布函数作为分段混合分布各段的拟合函数,通过极大似然估计算法获得分段混合分布的表达式。结合挖掘机土石挖掘工况,将本文方法应用到主泵出口压力载荷数据中,并与现有方法进行对比分析,本文方法得到的结果通过了卡方检验。同时,用1000组仿真数据来验证方法的可行性,得到了参数估计的误差仅为0~18%。
In order to solve the problem of load distribution in construction machines, an estimation method of piecewise mixed load distribution based on Akaike Information Criterion (AIC) K-means is proposed. First, according to Luise method, the chi-square test values of the normal distribution, logarithm normal distribution and Weibull distribution are calculated. Then, the corresponding distribution of the minimum test value is chosen as the fitting function of the piecewise mixed distribution. Finally, the formula expression of the distribution is obtained through the maximum likelihood estimation. The proposed method is applied to the outlet pressure load time history of the excavation operation the excavator, and compared with the existing method. The result obtained by the proposed method passes the chi-square test. The simulated data of 1000 groups are used to conduct feasibility analysis and the estimated parameter error range is 0~18%.
工程机械在作业过程中受到复杂多变工况的影响[1], 导致载荷分布具有明显的随机性和多样性[2]。获得较为准确的载荷分布是载荷谱外推的前提, 正态、威布尔等单一分布常被用来近似描述载荷的分布情况[3]。但是为了提升研究精度, 获得更接近实际分布情况的载荷分布, 单一分布已经不能够满足研究的需求。混合分布已受到越来越多的关注, 目前, 在各个领域已取得一些研究成果。Ni等[4]建立了焊接节点的应力谱模型, 基于EM算法对混合正态、混合对数以及混合威布尔的应力谱模型进行参数估计。Yang等[5]建立了数控机床的可靠性评估的混合威布尔模型, 并基于神经网络和EM算法对该混合模型进行参数估计。郑松林等[6]采用正态分布组合的方式, 建立了电驱动单元齿轮工作载荷的混合分布模型。Behrens等[7]建立了Gamma-GPD分段混合模型, 并采用贝叶斯方法进行了参数估计。Zheng等[8]在Behrens方法的基础上提出了移位Gamma-Generalized Pareto 分段混合分布, 建立了安全连续体模型, 以解决交通冲突与无干扰通行时间的分界线问题。陈道云等[9]基于实测动应力载荷数据, 根据不同分布函数在不同谱级段内体现出的拟合优势, 构建了分段函数的分布模型。
本文提出了一种分段混合分布估计的方法。首先, 将载荷数据分别按照几种常用分布函数进行卡方拟合检验, 将计算获得最小卡方值的分布函数作为本文提出的分段混合分布的各段拟合函数。然后, 根据AIC准则[10]确定混合分布的分段数, 采用K-means算法对载荷数据进行聚类划分。最后, 采用极大似然估计(MLE)算法, 将每一聚类的载荷数据按照各拟合函数的分布情况进行参数估计, 从而得到分段混合分布的表达式。
以常见的某型液压挖掘机为研究对象, 进行土石挖掘试验。挖掘机的主要操作是挖掘循环和行走, 为简化分析, 将履带位置固定, 挖掘机仅重复挖掘作业。具体操作模式是将油门固定于最大开度, 进行全挖掘深度、全挖掘半径、全速回转并90° 卸料。利用数据采集仪获得零部件的载荷-时间历程信息, 以15个挖掘循环进行一次数据统计。试验现场、样机及相关细节见图1。
本文主要针对主泵出口压力载荷, 提取其挖掘段载荷-时间历程信息, 开展载荷谱编制的相关研究。首先提取试验测得的数据转折点, 然后进行雨流计数, 得到均值和幅值载荷分布直方图[11]。根据载荷统计规律可知, 工程机械的载荷谱均值常服从正态分布, 幅值服从威布尔分布。图2为均、幅值载荷柱状图及其对应的拟合检验P-P图。
由图2可知, 载荷的均、幅值数据分布在代表理论分布的对角线附近, 很难直接判断其拟合效果。为得到定量性结论, 采用卡方检验判断多种常用模型的拟合效果, 如表1所示。
| 表1 卡方拟合检验结果 Table 1 Fitting results of Chi-square test |
通常采用p=0.05作为检验是否通过的临界值, 观察表1, 不论何种分布, 二者均未通过卡方检验, 且幅值的拟合效果更差。因此, 基于篇幅的考虑, 本文只对效果更差的幅值载荷进行进一步分析。针对幅值载荷, 从表1可以知道, 上述3种常用分布都不能够满足幅值载荷分布函数的拟合要求, 因此, 可考虑采用混合分布函数对幅值载荷进行拟合。
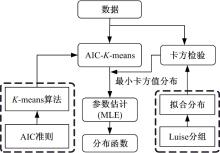
首先将测试数据代入几种常用的分布中, 得到该数据在单一分布下的卡方检验值; 随后选取最小的卡方检验值对应的分布作为分段混合分布的拟合函数; 然后, 利用AIC准则得到分段混合分布函数的分段数; 再采用聚类算法对实测数据进行分类; 最后, 将分类后的各组载荷数据按照对应的拟合函数进行极大似然估计, 从而得到分段混合分布函数的表达式。具体方法流程见图3。
当前工程机械载荷分布常用的几种函数分别是正态分布、对数正态分布以及威布尔分布, 概率密度函数分别如下:

式中:

式中:
式中:
进行数据拟合时, 卡方检验是最常用的检验准则, 主要用于对比观察值与拟合值的偏离程度, 见式(4):
式中:
在进行卡方拟合检验时, 采用Luise分组法[9]来确定载荷直方图的组距, 见式(5):
式中:
为了提高分布估计时的精度以及满足卡方检验的需求, 适当调整
利用分段函数组成的混合分布来描述载荷谱的分布情况, 其主要内容是将若干个不同参数的概率密度函数以截取的方式结合在一起组成新的概率密度函数。组成该分布函数的关键在于分段函数分段数的确定, 同时也是未知参数估计的前提。对于任一给定的数学模型, 有多种不同的确定函数个数的方法, 文献[10]已经对这些方法进行了阐述。其中AIC准则算法相较于其他方法更加稳定, 其结果也更加接近最优解。该准则是基于惩罚函数的思想提出的, 当纠正对数似然偏差降到最小时, 对应的个数就认为是函数的最优解, 即为本文所需模型的基本函数的个数。
式中:
K-means算法是一种广泛应用的聚类算法, 采用划分的方法将数据集中的对象按照某一种方式聚类到合适的簇中, 保证每个对象只属于一个簇。本文选取数据集中所有数据对象的误差平方和最小作为聚类依据。但是, 簇的数目是需要决策者按照以往经验进行指定。而AIC准则恰好解决了簇的个数问题。根据AIC准则得到段数为
式中:
首先对处理后的幅值数据进行卡方检验, 选取拟合的分布函数分别是正态分布、对数正态分布和威布尔分布。为保证每个组内具有充分多的数据, 此处选取3.35 MPa作为幅值载荷直方图的组距, 得到如图4所示的一维幅值谱。
观察表1, 结合临界卡方检验值9.49可知, 该幅值载荷不满足任何一种单一分布的拟合要求, 同时可知对数正态分布拟合下的卡方检验值最小。因此, 选取对数正态分布作为各分段函数的拟合函数。段数个数分别为1, 2, …, 10时, AIC的计算结果见图5。
因此当
| 表2 各组数据对数正态分布拟合参数估计值 Table 2 Estimated parameter values of each group by logarithmic normal distribution |
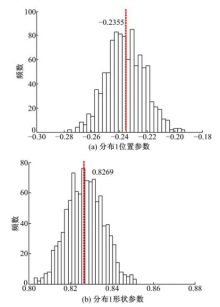
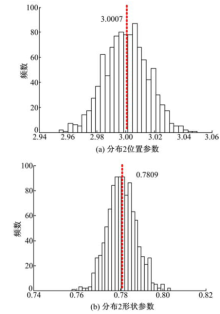
为验证本文方法的稳定性, 将本文方法应用到已知分布参数的仿真数据中。已知3组各5000个数据分别服从N1~(0, 1)(分布1), N2~(3, 1)(分布2)和N3~(6, 1)(分布3)。对数据进行截取, 在服从N1~(0, 1)分布的数据中选取小于1的数据; 服从
结合图6~图8可知, 对于1000组仿真数据, 利用聚类法得到的3个分布的参数估计值的分布接近正态分布, 采用上述直方图的均值代表各估计值, 与原均值的对比结果见表3。由于仿真数据的生成具有随机性, 截取后的位置参数值会发生偏移, 而分布2两边截取, 偏移程度相抵消。同时, 数据量的变化使形状参数发生改变。因此结合表1可知, 估计值在原值附近发生不同程度的偏移, 且偏移倍数在[0.82, 1.04]内, 造成的误差为0~18%。
| 表3 参数估计结果分析 Table 3 Analysis of parameter estimation values |
随机选取一组仿真数据分析观察数据拟合效果, 数据总样本量为131 908, 取值范围为[-4.2486, 10.2170]。3个分布选取样本量分别为42 188、47 739以及41 981, 取值范围分别为[-4.2486, 0.9998]、[1.0001, 4.9997]、[5.0002, 10.2170]。
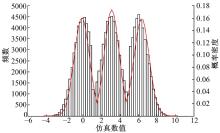
对数据进行聚类后得到3组数据的取值分别为[-4.2486, 1.3848]、[1.3857, 4.6214]、[4.6220, 10.2170], 样本量分别为43 678、44 767以及43 463。通过MLE得到正态分布的参数估计值见表4。
| 表4 各组数据正态分布拟合参数估计值 Table 4 Estimated parameter values of each group by normal distribution |
根据参数估计结果得到数据拟合效果见图9。
根据文献[9]提出的方法, 本文依旧选取上述3种分布函数进行函数分布估计。单一分布函数的拟合参数值见表5。
| 表5 单一分布函数和分段函数拟合参数估计值 Table 6 Estimated parameter values of each group by single distribution function and piecewise function |
根据表5的参数值, 可以得到每一级的卡方值, 并将各级的最小卡方值标记出, 绘成图10。
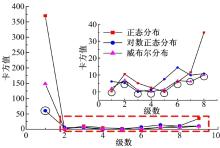 | 图10 三种分布函数拟合检验的各级卡方值Fig.10 Chi-square value of each level obtained by three kinds of distribution function fitting test |
从图10中可以看出, 对前5级数据, 采用对数正态分布拟合较好, 正态分布拟合第6、7级较好, 威布尔分布对尾部数据(即8、9级数据)拟合较好。将载荷数据分成3部分, 分别进行对数正态、正态以及威布尔分布的参数估计, 进而得到式(7)中的参数估计结果见表5。
根据参数估计值以及式(4)得到分段函数各级卡方值及总卡方值, 见表6。由表6可知, 分段函数的各级卡方检验值及总卡方检验值(ZK)在一定程度上明显小于单一分布时的卡方检验量, 但分段函数的总卡方值大于此分布下的临界卡方检验值(LK), 因此该分段函数没有通过卡方检验。
| 表6 分段函数的卡方拟合检验值 Table 6 Chi-square test values of piecewise function |
为验证本文方法对拟合函数的依赖性, 各分段函数比例系数不变, 分别选取正态分布和威布尔分布作为本文方法的各段拟合函数。分别计算得到的参数估计值见表7。
| 表7 各组数据正态分布和威布尔分布拟合参数 Table 7 Estimated parameter values of each group by normal and Weibull distribution function |
同时, 得到卡方检验值见表8。
| 表8 分段混合正态及混合威布尔分布的卡方检验值 Table 8 Chi-square test values of piecewise mixed normal and Weibull distribution |
利用本文方法, 改变分段混合分布函数的拟合函数类型。根据单一分布时的拟合卡方检验值, 当选取卡方检验值略大于对数正态分布的威布尔分布为各段的拟合函数, 依旧可以得到符合拟合条件的分段混合分布函数。正态分布对应的卡方检验值是对数正态分布卡方值的2倍以上, 当拟合函数为正态分布时, 不能够通过卡方检验。因此可知, 当拟合函数发生改变时, 本文方法也能得到较好的结果。从而证明本文方法具有较广的拟合函数适用范围。
(1)提出了一种基于AIC-K-means方法的分段混合分布函数的估计方法。利用AIC准则来确定混合分布函数的分段数, 通过K-means法将数据进行聚类划分。根据工程机械常有的几种分布, 利用Luise分组法进行卡方检验, 选取最小卡方检验值对应的分布作为各段的拟合分布。
(2)将本文方法应用到工程机械挖掘机主泵载荷数据中, 所得分段混合分布通过了卡方检验, 证明本文方法具有可行性。
(3)将本文方法应用到1000组仿真数据中, 结果表明本文方法误差为0~18%。
(4)通过改变分段混合分布的拟合函数类型, 计算结果表明本文方法具有较广的拟合函数适用范围, 有利于提高拟合效率。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|