整体抽油杆柱在油管内空间屈曲的多段式仿真模型对比

引用本文

孙秀荣, 董世民, 王宏博, 李伟成, 孙亮. 整体抽油杆柱在油管内空间屈曲的多段式仿真模型对比[J].吉林大学学报（工学版）, 2018,48(4): 1124-1132
SUN Xiu-rong, DONG Shi-min, WANG Hong-bo, LI Wei-cheng, SUN Liang. Comparison of multistage simulation models of entire sucker rod with spatial buckling in tubing[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 1124-1132 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170512
Permissions

整体抽油杆柱在油管内空间屈曲的多段式仿真模型对比

孙秀荣, 董世民, 王宏博, 李伟成, 孙亮

燕山大学机械工程学院,河北秦皇岛 066004

通讯作者:董世民(1962-),男,教授,博士.研究方向:机械采油系统动态仿真与运行优化.E-mail:ysudshm@163.com

作者简介:孙秀荣(1984-),女,博士研究生.研究方向:油气井杆柱力学.E-mail:sunxiurong84@163.com

基金:河北省自然科学基金项目(E201703101); 国家自然科学基金项目 (51174175).

摘要

针对直井抽油机井杆管偏磨进行分析,将整体抽油杆柱在油管内的空间屈曲模型分为三段式、四段式和五段式,并分别建立了每种模型下每段的数学微分方程,给出连接点处的位移、转角、弯矩、切向剪力的连续性条件。基于数值积分法对每段的方程进行求解,并将数学模型最终转化为非线性代数方程组的数值仿真模型,实现了对整体抽油杆柱屈曲构型的数值仿真。仿真结果表明:当工程实际中杆柱泵端载荷远远超过空间屈曲临界载荷时,五段式建立整体杆柱空间屈曲模型比三段式和四段式更为合理;三段式和四段式屈曲模型在螺旋段接触力、螺旋段长度、悬臂段的位置与五段式都有一定差距;先前的研究中将螺旋段方程进行降阶简化,与本文的完整螺旋段屈曲方程求解相比,模型简化得到的螺旋段分布接触力和螺旋段的长度结果相差较大。不同的分段方式,杆管偏磨的位置、接触压力就不同,本文仿真方法为深入研究杆管偏磨和杆柱寿命预测奠定了理论基础。

关键词: 机械设计; 抽油杆柱; 空间屈曲; 五段式; 边界约束; 数值积分

中图分类号:TB121;TE355.5 文献标志码:A 文章编号:1671-5497(2018)04-1124-09

Comparison of multistage simulation models of entire sucker rod with spatial buckling in tubing

SUN Xiu-rong, DONG Shi-min, WANG Hong-bo, LI Wei-cheng, SUN Liang

School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China

Abstract

The spatial buckling of sucker rod in tubing is important basis to analyze rod and tubing wear in vertical pumping well. In this paper, first, the spatial buckling model of entire sucker rod is divided into three-section model, four-section model and five-section model. Then the differential equations of each section of each model are established, and the continuity conditions of the displacement, rotation angle, bending moment and the tangential shear at the connecting points are derived respectively. Finally, numerical integration method is used to solve the equations, in which the differential equations are transferred into nonlinear algebraic equations, thus, the numerical simulation of the entire bucking configuration of sucker rod string is realized. The simulation results show that, when the bump end load of the rod is much higher than the spatial buckling critical load, the five-section model is more reasonable than the three- and four-section models. The contact force, helix angle of the helical section, the length of the helical section and bottom suspend section of three- and four-section models have certain gaps with five-section model. The results errors of the distribution contact force and the length of the helical section obtained by simplified reduced order equations in previous studies are larger compared with the solution of the complete helical buckling section equation. The wear position and contact pressure are different with different subsection methods. The simulation method may provide reference for further study of rod and tubing wear and prediction of rod life.

Keyword: mechanical design; sucker rod string; spatial buckling; five-section; boundary constraint; numerical integration

文章图片

0 引言

杆管偏磨是抽油机井常见的井下故障。杆管偏磨不仅降低了油井产量, 而且缩短了检泵周期, 增加了油井检泵作业费用。研究杆管偏磨原因和治理技术、延长检泵周期对于降低管偏磨率, 降低采油成本, 提高油田开发效益, 具有重要的实际意义。

抽油杆柱在油管内屈曲临界载荷和构型的分析计算方法是直井抽油机井杆管偏磨分析的理论基础^[1]。直井抽油杆柱在油管内的屈曲问题属于石油工程领域的细长杆柱在铅直圆筒内的屈曲力学问题。国内外专家学者对细长杆柱在铅直圆筒内屈曲理论进行了系统研究。研究结果表明, 细长杆柱在铅直圆筒内的屈曲构型分为两类:轴向压力较小时的平面屈曲构型^{[1, 2, 3, 4, 5]}; 轴向压力较大时的空间屈曲构型^{[6, 7, 8, 9]}。当考虑边界条件的影响时, 细长杆柱在铅直圆筒内的空间屈曲构型可由三段、四段或五段组成^{[6, 7, 8, 9]}:底部空间梁段(1或2段)、中间螺旋段、顶部空间梁段(1或2段)。文献[6, 7]以螺旋段杆柱为研究对象, 未考虑两端空间梁变形及边界条件影响, 建立了螺旋段屈曲构型的仿真方法; 文献[8, 9]以底部空间梁段与中间螺旋段杆柱为研究对象, 但仍然是按文献[6, 7]所建立的方法独立求解螺旋段杆柱的屈曲构型, 然后根据螺旋段与悬臂梁段弯曲变形的连续性条件, 并考虑边界条件的影响, 建立了悬臂梁段弯曲变形的仿真方法, 仿真模型没有反映出边界条件、两端空间梁段弯曲变形对螺旋段屈曲构型的影响; 文献[10, 11, 12, 13, 14, 15, 16, 17, 18, 19]以底部空间梁段与中间螺旋段杆柱为研究对象, 建立了空间梁段与中间螺旋段杆柱的弯曲微分方程, 并考虑了边界条件以及空间梁段与中间螺旋段弯曲变形的连续性条件, 建立了底部空间梁段与中间螺旋段构型仿真的数学模型, 但没有严格基于数学方法建立系统的数值仿真模型, 而是基于假设和简化对中间螺旋段的四阶弯曲常微分方程进行了降阶处理, 计算结果仅仅讨论了边界条件对底部空间梁段长度的影响, 没有反映出边界条件对螺旋屈曲构型的影响。

因此, 作者针对以下问题进行了研究:①抽油杆柱在油管内的整体屈曲构型由几段组成比较接近实际而误差更小; ②不同的分段形式对杆柱构型和杆管接触产生什么影响; ③简化的螺旋段方程与严格基于数学方法求解的完整方程所求结果相差多大; ④边界条件对杆柱整体构型有无影响。

根据抽油机井杆管偏磨分析的实际需要, 本文从整体杆柱的角度出发, 考虑边界条件的影响, 建立了完整的杆柱屈曲方程, 并严格基于连接点处的位移、转角、弯矩和切向剪力建立相邻段间的连续性条件, 克服了非线性方程求解的问题, 形成了整体杆柱空间屈曲的仿真模型。与先前研究过程中杆柱屈曲三段式、四段式和五段式的模型问题进行仿真对比, 最后给出结论。

本文研究杆柱屈曲的实际意义在于防止抽油机井杆管偏磨, 但抽油机井井筒为油气水多相混合液, 流体密度与黏度沿井深变化, 导致杆柱所受的轴向分布载荷(杆柱自重)沿井深变化, 因而在本文数学模型中可将轴向分布载荷作为随井深变化的参数进行计算, 这为杆管偏磨的下一步研究奠定了新的理论基础。

1 三段式杆柱屈曲力学和数学模型

1.1 力学模型

为便于研究, 做如下假设和简化:

(1) 油井为铅垂直井, 杆柱与井眼中心线重合。

(2) 抽油杆柱顶端简化为固定端或铰接端; 杆柱底端简化为可滑动的固定端或铰接端。

(3) 杆柱变形为线弹性范围内的小变形, 忽略杆柱扭矩的影响。

(4) 杆柱为等直径D(单位m)的均质杆, 杆柱长度为L(单位m)、弹性模量为E(单位N/m²)、抗弯惯性矩为I(单位m⁴); 油管内径为D_t(单位m); 油管内圆半径与杆柱半径的差值为r₀。

(5) 杆柱受非均匀轴向分布力q(x), 合适条件下可简化为均布力; 杆柱泵端受集中轴向压力F(单位N)的作用。

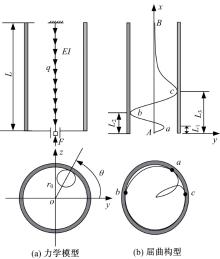
在上述假设和简化条件下, 建立图1所示的杆柱屈曲分析的力学模型及空间屈曲构型示意图。

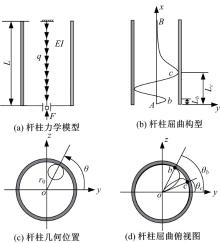	Figure Option View Download New Window
	图1 抽油杆柱三段式力学模型和屈曲构型图Fig.1 Mechanical model and buckling configuration of sucker rod string divided into three sections

为便于数学建模, 建立两个坐标系, 一是描述两端悬臂梁段弯曲变形的空间直角坐标系, 即两端空间梁任意轴向位置x处的横向挠度为y、z, 如图1(b)、图1(c)所示; 二是描述螺旋段弯曲变形的极坐标系, 即螺旋段任意轴向位置x处的极角为θ , 如图1(c)所示; 螺旋切入与切出点的轴向位置分别为L_b(单位m)、L_c(单位m), 所对应的极角分别为θ _b、θ _c, 如图1(b)、图1(d)所示。

杆柱屈曲构型仿真的数学模型由各段杆柱的弯曲变形微分方程、边界条件、连续性条件与约束条件组成。

1.2 数学模型

1.2.1 中间螺旋屈曲(bc段)方程

根据微元受力分析可得抽油杆柱在油管内螺旋屈曲的弯曲变形微分方程为:

$\{\begin{array}{l} EI \frac{d^{4} y}{d x^{4}} + (F_{x} \frac{d y}{d x}) \frac{'}{} + N_{r} \cos θ = 0 \\ EI \frac{d^{4} z}{d x^{4}} + (F_{x} \frac{d z}{d x}) \frac{'}{} + N_{r} \sin θ = 0 \end{array}$ (1)

式中:F_x为截面x处杆柱的轴向压力; F_x=F- $\int_{0}^{x}$ q(x)dx, N; N_r为单位长度杆柱的径向接触分布压力, N/m。

用极坐标 $θ$ 表示的螺旋屈曲段杆柱弯曲微分方程、杆柱与油管之间接触力方程分别为^[3]:

$EI θ^{(4)} - 6 EIθ'^{2} θ″ + (F_{x} θ')' = 0$ (2)

$N_{r} = r_{0} EI (- θ'^{4} + 3 θ ″^{2} + 4 θ'θ‴) + r_{0} F_{x} θ'^{2}$ (3)

1.2.2 底部空间梁(Ab段)方程

对于底部的空间梁段杆柱, 接触压力N_r=0。由式(1)可得底部空间梁段杆柱的弯曲微分方程为:

$\{\begin{array}{l} EI \frac{d^{4} y}{d x^{4}} + \frac{d}{d x} (F_{x} \frac{d y}{d x}) = 0 \\ EI \frac{d^{4} z}{d x^{4}} + \frac{d}{d x} (F_{x} \frac{d z}{d x}) = 0 \end{array} x_{A} < x < x_{b}$ (4)

1.2.3 上部空间梁(cB段)方程

同式(4), 可得底部空间梁段杆柱弯曲微分方程为:

$\{\begin{array}{l} EI \frac{d^{4} y}{d x^{4}} + \frac{d}{d x} (F_{x} \frac{d y}{d x}) = 0 \\ EI \frac{d^{4} z}{d x^{4}} + \frac{d}{d x} (F_{x} \frac{d z}{d x}) = 0 \end{array} x_{c} < x < x_{B}$ (5)

1.2.4 边界条件

杆柱顶端和泵端均为固定端的边界条件为:

$\{\begin{array}{l} u_{A, B} = v_{A, B} = 0 \\ u'_{A, B} = v'_{A, B} = 0 \end{array}$ (6)

杆柱顶端和泵端均为铰接端的边界条件为:

$\{\begin{array}{l} u_{A, B} = v_{A, B} = 0 \\ u ″_{A, B} = v ″_{A, B} = 0 \end{array}$ (7)

1.2.5 连续性条件

接触点b处的连续性条件包括:几何连续(位移和转角)、弯矩连续、切向剪力连续, 分别为:

$\{\begin{array}{l} y_{b} = r_{0} \cos θ_{b} \\ z_{b} = r_{0} \sin θ_{b} \\ y'_{b} = - r_{0} \sin θ_{b} θ'_{b} \\ z'_{b} = r_{0} \cos θ_{b} θ'_{b} \end{array}$ (8)

$\{\begin{array}{l} y ″_{b} = - r_{0} \cos θ_{b} θ'_{b}^{2} - r_{0} \sin θ_{b} θ ″_{b} \\ z ″_{b} = - r_{0} \sin θ_{b} θ'_{b}^{2} + r_{0} \cos θ_{b} θ ″_{b} \end{array}$ (9)

$\begin{array}{l} \{\begin{array}{l} EIy ‴_{b} + F_{x_{b}} y'_{b} - EI (r_{0} \sin θ_{b} θ'_{b}^{3} - 3 r_{0} \cos θ_{b} θ'_{b} θ ″_{b} - \\ r_{0} \sin θ_{b} θ ‴_{b}) + F_{x_{b}} r_{0} \sin θ_{b} θ'_{b} - \cos θ_{b} \int_{L_{b}}^{L_{c}} N_{r} d x = 0 \\ EIz ‴_{b} + F_{x_{b}} z'_{b} - EI (- r_{0} \cos θ_{b} θ'_{b}^{3} - 3 r_{0} \sin θ_{b} θ'_{b} θ ″_{b} + \\ r_{0} \cos θ_{b} θ ‴_{b}) - F_{x_{b}} r_{0} \cos θ_{b} θ'_{b} - \sin θ_{b} \int_{L_{b}}^{L_{c}} N_{r} d x = 0 \end{array} \end{array}$ (10)

式(10)中含有径向接触分布压力函数N_r(x)。消去函数N_r(x), 可将剪力连续性条件简化为:

$\begin{array}{l} [EIy ‴_{b} + F_{xb} y'_{b} - EI (r_{0} \sin θ_{b} θ'_{b}^{3} - 3 r_{0} \cos θ_{b} θ'_{b} θ ″_{b} - \\ r_{0} \sin θ_{b} θ ‴_{b}) + F_{xb} r_{0} \sin θ_{b} θ'_{b}] \sin θ_{b} = \\ [EIz ‴_{b} + F_{xb} z'_{b} - EI (- r_{0} \cos θ_{b} θ'_{b}^{3} - 3 r_{0} \sin θ_{b} θ'_{b} θ ″_{b} + \\ r_{0} \cos θ_{b} θ ‴_{b}) - F_{xb} r_{0} \cos θ_{b} θ'_{b}] \cos θ_{b} \end{array}$ (11)

同理, 杆柱螺旋屈曲段与上部空间梁段接触点c处的连续性条件为:

$\{\begin{array}{l} y_{c} = r_{0} \cos θ_{c} \\ z_{c} = r_{0} \sin θ_{c} \\ y'_{c} = - r_{0} \sin θ_{c} θ'_{c} \\ z'_{c} = r_{0} \cos θ_{c} θ'_{c} \\ y ″_{c} = - r_{0} \cos θ_{c} θ'_{c}^{2} - r_{0} \sin θ_{c} θ ″_{c} \\ z ″_{c} = - r_{0} \sin θ_{c} θ'_{c}^{2} + r_{0} \cos θ_{c} θ ″_{c} \\ [y ‴_{c} + F_{xc} y'_{c} - (r_{0} \sin θ_{c} θ'_{c}^{3} - 3 r_{0} \cos θ_{c} θ'_{c} θ ″_{c} - \\ r_{0} \sin θ_{c} θ ‴_{c}) + F_{xc} r_{0} \sin θ_{a} θ'_{a}] \sin θ_{c} = \\ [z ‴_{c} + F_{xc} v'_{c} - (- r_{0} \cos θ_{c} θ^{3}'_{c} - 3 r_{0} \sin θ_{c} θ'_{c} θ ″_{c} + \\ r_{0} \cos θ_{c} θ ‴_{c}) - F_{xc} r_{0} \cos θ_{c} θ'_{c}] \cos θ_{c} \end{array}$ (12)

1.3 数值算法

式(4)和式(5)为4个四阶齐次变系数线性常微分方程, 无法求得精确的解析解, 可以基于积分法求其数值解; 式(2)为较复杂的四阶非线性常微分方程, 只能求其数值解。本文基于四阶Runge-Kutta法建立以上5个常微分方程的数值仿真模型。以两端固定边界约束条件为例, 具体仿真算法如下:

(1) 将未知的悬臂段无因次长度L_b、L_c表示为x₁、x₂, 即x₁=L_b、x₂=L_c。

(2) 底部悬臂梁两个常微分方程的边界条件(即数值积分在x=0处的初值条件)表示为:

$\{\begin{array}{l} {y_{A}, y'_{A}, y ″_{A}, y ‴_{A}} = {0, 0, x_{3}, x_{4}} \\ {z_{A}, z'_{A}, z ″_{A}, z ‴_{A}} = {0, 0, x_{5}, x_{6}} \end{array}$ (13)

仿真计算时, 假设未知参数x₁、x₂、x₃、x₄、x₅、x₆的初值, 则可以完成方程(4)的数值仿真计算, 并计算得到悬臂梁上b点的仿真结果为:

$\{y_{b}, y'_{b}, y ″_{b}, y ‴_{b}, z_{b}, z'_{b}, z ″_{b}, z ‴_{b}\}$ (14)

由于未知参数x₁、x₂、x₃、x₄、x₅、x₆的初值是任意假定的, 因此仿真结果式(14)不一定能满足连续性条件式(8)~(11), 以下继续迭代。

(3) 为启动螺旋段微分方程(2)的数值仿真, 假设螺旋段切入点b的边界条件为:

$\{θ_{b}, θ'_{b}, θ ″_{b}, θ ‴_{b}\} = \{x_{7}, x_{8}, x_{9}, x_{10}\}$ (15)

根据上述边界条件完成方程(4)的数值仿真计算, 并计算得到螺旋段上c点的仿真结果:

$\{θ_{c}, θ'_{c}, θ ″_{c} θ ‴_{c}\}$ (16)

(4) 顶部悬臂梁两个常微分方程的边界条件(即数值积分在x=L处的初值条件)为:

$\{\begin{array}{l} \{y_{B}, y'_{B}, y ″_{B}, y ‴_{B}\} = \{0, 0, x_{11}, x_{12}\} \\ \{z_{B}, z'_{B}, z ″_{B}, z ‴_{B}\} = \{0, 0, x_{13}, x_{14}\} \end{array}$ (17)

假设未知参数x₁₁、x₁₂、x₁₃、x₁₄的初值, 根据上述边界条件, 完成方程(5)的数值仿真计算, 并计算得到悬臂梁上c点的仿真结果为:

$\{y_{c}, y'_{c}, y ″_{c}, y ‴_{c}, z_{c}, z'_{c}, z ″_{c}, z ‴_{c}\}$ (18)

将假设的边值 ${x_{1}, x_{2}, \dots, x_{14}} 、$ 连续点仿真结果(式(14)(16)(18))以及杆柱构型仿真结果分别代入连续性条件(8)~(12), 则得到14个关于边值 $\bar{X} = {x_{1}, x_{2}, \dots, x_{14}}^{T}$ 的代数方程组, 简化表示为:

$\{\begin{array}{l} f_{1} = f_{1} (\bar{X}) = 0 \\ f_{2} = f_{2} (\bar{X}) = 0 \\ ︙ \\ f_{14} = f_{14} (\bar{X}) = 0 \end{array}$ (19)

式(19)为非线性代数方程组, 无法求得解析解。本文采用最小二乘法求其数值解。

2 四段式杆柱屈曲力学和数学模型

2.1 力学模型

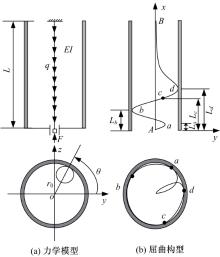
力学模型的简化同1.1节, 在上述假设和简化条件下, 建立图2(a)所示的四段式杆柱屈曲分析的力学模型和图2(b)所示的杆柱空间屈曲构型示意图。

	Figure Option View Download New Window
	图2 抽油杆柱四段式力学模型和屈曲构型图Fig.2 Mechanical model and buckling configuration of sucker rod string divided into four sections

2.2 数学模型

中间螺旋屈曲(bc段)微分方程和接触力方程分别同式(2)和式(3); 底部空间梁柱Aa段、ab段、上部空间梁柱cB段的空间微分方程均与式(7)相同。因此四段式整体杆柱屈曲微分方程全部建立, 下面介绍边界条件和每段间的连续性条件。杆柱顶端和底端的边界条件同1.2.4节, ab段和bc段的连接处b点的连续性条件同式(8)~(11), bc段和cB段的连接处c点的连续性条件同式(12), 此处不再给出。Aa段和ab段的连接处a点的连续性条件需满足几何连续、弯矩连续和切向剪力连续, 即:

$\{\begin{array}{l} y_{a +} = r_{0} \cos θ_{a} \\ z_{a +} = r_{0} \sin θ_{a} \\ y'_{a +} = - r_{0} \sin θ_{a} θ'_{a} \\ z'_{a +} = r_{0} \cos θ_{a} θ'_{a} \end{array}$ (20)

$\{\begin{array}{l} y_{a -} = r_{0} \cos θ_{a} \\ z_{a -} = r_{0} \sin θ_{a} \\ y'_{a -} = - r_{0} \sin θ_{a} θ'_{a} \\ z'_{a -} = r_{0} \cos θ_{a} θ'_{a} \end{array}$ (21)

$\{\begin{array}{l} y ″_{a -} = y ″_{a +} \\ z ″_{a -} = z ″_{a +} \\ [EIy ‴_{a -} + F_{xa} y'_{a -} - EIy ‴_{a +} - F_{xa} y'_{a +}] \sin θ_{a} = \\ [EIz ‴_{a -} + F_{xa} z'_{a -} - EIz ‴_{a +} - F_{xa} z'_{a +}] \cos θ_{a} \end{array}$ (22)

2.3 数值算法

(1) 将未知的悬臂段无因次长度L_a、L_b、L_c表示为x₁、x₂、x₃, 即x₁=L_a、x₂=L_b、x₃=L_c。

(2) 底部悬臂梁两个常微分方程的边界条件(即数值积分在x=0处的初值条件)表示为:

$\{\begin{array}{l} \{y_{A}, y'_{A}, y_{a}, y'_{a}\} = \{0, 0, x_{4}, x_{5}\} \\ \{z_{A}, z'_{A}, z_{a}, z'_{a}\} = \{0, 0, x_{6}, x_{7}\} \end{array}$ (23)

仿真计算时, 假设未知参数x₁、x₂、x₃、x₄、x₅、x₆、x₇的初值, 则可以完成Aa段方程的数值仿真计算, 并计算得到悬臂梁上a点的仿真结果为:

$\{\begin{array}{l} \{y_{a -}, y'_{a -}, y ″_{a -}, y ‴_{a -}\} \\ \{z_{a -}, z'_{a -}, z ″_{a -}, z ‴_{a -}\} \end{array}$ (24)

由于未知参数x₁、x₂、x₃、x₄、x₅、x₆、x₇的初值是任意假定的, 因此仿真结果式(24)不一定能满足a点的连续性条件。

(3) 启动底部空间梁柱ab段的数值仿真, ab段上无限趋近于a点处的边界条件表示为:

$\{\begin{array}{l} \{y_{a +}, y'_{a +}, y ″_{a +}, y ‴_{a +}\} = \\ \{r_{0} \cos x_{8}, - r_{0} x_{9} \sin x_{8}, x_{10}, x_{11}\} \\ \{z_{a +}, z'_{a +}, z ″_{a +}, z ‴_{a +}\} = \\ \{r_{0} \sin x_{8}, r_{0} x_{9} \cos x_{8}, x_{12}, x_{13}\} \end{array}$ (25)

式中:x₈=θ _a , x₉=θ '_a。

同方程(24), ab段上b点处的仿真结果为:

$\{\begin{array}{l} \{y_{b -}, y'_{b -}, y ″_{b -}, y ‴_{b -}\} \\ \{z_{b -}, z'_{b -}, z ″_{b -}, z ‴_{b -}\} \end{array}$ (26)

(4)启动螺旋屈曲bc段的数值仿真, bc段上无限无限趋近于b点处的边界条件表示为:

$\{θ_{b}, θ'_{b}, θ ″_{b}, θ ‴_{b}\} = \{x_{14}, x_{15}, x_{16}, x_{17}\}$ (27)

同理, 可得到bc段上c点处的仿真结果为:

$\{θ_{c}, θ'_{c}, θ ″_{c}, θ ‴_{c}\}$ (28)

(5)启动cB段的数值仿真, 顶点B处的边界条件表示为:

$\{\begin{array}{l} \{y_{B}, y'_{B}, y_{c}, y'_{c}\} = \{0, 0, x_{18}, x_{19}\} \\ \{z_{B}, z'_{B}, z_{c}, z'_{c}\} = \{0, 0, x_{20}, x_{21}\} \end{array}$ (29)

可得到 $cB 段上 c$ 点处的仿真结果为:

$\{\begin{array}{l} \{y_{c}, y'_{c}, y ″_{c}, y ‴_{c}\} \\ \{z_{c}, z'_{c}, z ″_{c}, z ‴_{c}\} \end{array}$ (30)

将假设的边值 ${x_{1}, x_{2}, \dots, x_{21}} 、$ 连续点仿真结果式(24)(26)(28)(30)以及杆柱构型仿真结果分别代入b点、c点以及a点的连续性条件式(8)~(12)、(20)~(22), 则得到21个关于边值 $\bar{X} = {x_{1}, x_{2}, \dots, x_{21}}^{T}$ 的代数方程组, 求解方法同1.3节。

3 五段式杆柱屈曲力学和数学模型

3.1 力学模型

力学模型的简化同1.1节, 在上述假设和简化条件下, 建立图3(a)所示的五段式杆柱屈曲分析的力学模型; 图3(b)为杆柱空间屈曲构型示意图。

	Figure Option View Download New Window
	图3 抽油杆柱五段式力学模型和屈曲构型图Fig.3 Mechanical model and buckling configuration of sucker rod string divided into five sections

3.2 数学模型

中间螺旋屈曲(bc段)微分方程和接触力方程分别同式(2)和式(3); 底部空间梁柱Aa段、ab段、上部空间梁柱cd段、dB段的空间微分方程均与式(4)相同。杆柱顶端和底端的边界条件同1.2.4节, Aa段和ab段的连接处a点的连续性条件、cd段和dB段的连接处d点的连续性条件均与式(20)~(22)相同, ab段和bc段的连接处b点的连续性条件、bc段和cB段的连接处c点的连续性条件均与式(12)相同。需满足几何连续、弯矩连续和切向剪力连续, 因此五段式整体杆柱屈曲微分方程和边界连续性条件全部建立。

3.3 数值算法

与2.2节采用相同的计算方法, 但在其基础上再引入7个未知量, 整体杆柱屈曲构型的求解转化为28个未知数组成的28个非线性代数方程组的求解。

4 仿真结果及分析

仿真计算的基本参数为:杆柱直径D=0.025 m; 杆柱弹性模量E=209 GPa; 轴向分布载荷q=25 N/m; 油管与抽油杆柱径向间隙r₀=0.0185 m。

4.1 接触力对比结果

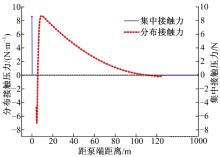
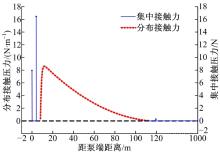
分别计算杆柱在三段式、四段式下的完全螺旋段上的接触力分布情况。边界条件采用两端固定, 杆柱长度为1000 m, 轴向压力为3000 N, 仿真结果分别见图4、图5。由图4可知, 杆柱完全螺旋段上的分布接触力在螺旋切入点和切出点附近都产生了负值, 接触力为负值的情况实际并不存在, 产生负值说明杆柱与油管并未接触上, 在此处还应是悬空段, 因此三段式建立杆柱屈曲模型得出完全螺旋段误差较大, 应建立四段式或五段式。图5在螺旋切出点附近存在与图4相似的问题, 进一步证明四段式建立杆柱屈曲模型与实际仍然存在一定误差。

	Figure Option View Download New Window
	图4 三段式完全螺旋段接触力分布Fig.4 Contact force distribution of helical section for three-section model

	Figure Option View Download New Window
	图5 四段式完全螺旋段接触力分布Fig.5 Contact force distribution of helical section for four-section model

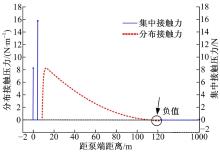
由上可知, 三段式和四段式建立杆柱屈曲模型与实际模型相差较大, 图6给出了五段式杆柱接触力分布情况。由图6可知, 完全螺旋段上的分布接触力都为正值, 说明完全螺旋段上杆柱处处与油管接触在此模型下建立屈曲模型较为合理; 泵端约束反力、接触点a处集中力较大, 接触点b处集中力和顶端约束反力值相比螺旋段分布接触力则很小。杆柱与油管的接触力分析是研究杆管偏磨的基础, 图6说明应将泵筒与油管处集中接触力、底端杆柱与油管集中接触力、螺旋段分布接触力综合考虑到杆柱偏磨中去。

	Figure Option View Download New Window
	图6 五段式完全螺旋段接触力分布Fig.6 Contact force distribution of helical section for five-section model

4.2 不同分段模型对螺旋段和底部悬空段的影响

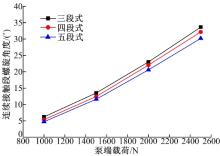
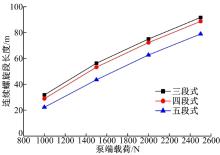
图7、图8和表1进一步给出了两端固定边界, 但在不同的分段模型下, 螺旋段和底部悬空段的变化规律。由图7、图8可知, 在相同的参数下, 三段和四段的连续接触段的螺旋角和螺旋段长度均比五段式的对应值大。表1可得出随着载荷的增大, 三、四、五段模型中第一个接触点的位置都逐渐降低, 其中五段式对应位置比三、四段更低。综合4.1节可得出结论:在下冲程接近实际泵端载荷的情况下, 五段式建立杆柱屈曲模型在螺旋段角度、长度和底部悬臂段的长度方面比三、四段更精确。

	Figure Option View Download New Window
	图7 完全螺旋段角度随泵端载荷变化Fig.7 Angle of helical section varies with bump load

	Figure Option View Download New Window
	图8 完全螺旋段长度随泵端载荷变化Fig.8 Length of helical section varies with bump load

表1 底端悬臂段L_a结果 Table 1 Calculation results of L_a in bottom suspend section

4.3 与简化模型结果对比

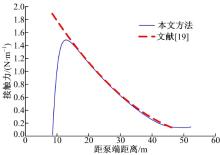
目前, 学者对杆柱空间屈曲进行的研究都是将螺旋段复杂的非线性微分方程进行简化处理而得到的近似结果^{[10, 11, 12, 13, 14, 15, 16, 17, 18, 19]}, 与实际有较大出入。表2和图9分别给出了本文完整模型和文献[19]简化模型的对比结果。基本参数与前文相同, 但杆长取92.3 m, 泵端压力为1493 N。由表2和图9可知, 简化模型得到的底部两端悬臂段的长度差别较小, 但完全螺旋段的长度和对应的分布接触力结果相差较大, 尤其是分布接触力。简化模型得到的分布接触力由螺旋切入点处单调递减, 而本文则是单调递增大, 再单调递减, 二者结果在螺旋切入处相差甚大。因此, 当用于杆管偏磨压力的分析计算时, 简化模型误差较大, 而本文结果更精确。

表2 计算结果对比 Table 2 Comparison of calculation results

	Figure Option View Download New Window
	图9 完全螺旋段分布接触力对比Fig.9 Comparison of distribution contact force in complete helical section

5 结束语

本文将整体抽油杆柱在油管内的空间屈曲模型分为三段式、四段式和五段式, 并分别建立了每种模型下每段的数学微分方程, 连接点处的位移、转角、弯矩、切向剪力的连续性条件, 实现了对整体抽油杆柱屈曲构型的数值仿真。仿真结果表明, 所形成的抽油杆柱屈曲构型的数值仿真方法是可行的。当工程实际中杆柱泵端载荷远远超过空间屈曲临界载荷时, 五段式建立杆柱屈曲模型仿真结果比三、四段式更为精确。主要体现在杆管间接触压力的分布规律和压力大小上。先前的研究中将螺旋段方程进行降阶简化, 与本文的完整方程求解结果相比, 简化的模型对螺旋段分布载荷和螺旋段的长度都产生较大影响, 因此螺旋段微分方程求解不宜简化。不同的分段方式, 杆管偏磨的位置、接触压力就不同, 作者建立的仿真方法为深入研究杆管偏磨和杆柱寿命预测奠定了理论基础。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	董世民. 水驱抽油机井杆管偏磨原因的力学分析[J]. 石油学报, 2003, 24(4): 108-112. Dong Shi-min. Mechanical analysis on causes of worn rod string and tubing of rod pumping wells in the water-flooding oilfield[J]. Acta Petrolei Sinica, 2003, 24(4): 108-112. [本文引用:2]
[2]	Lubinski A. A study of the buckling of rotary drilling string[J]. Drilling and Production Practice, 1950: 178-214. [本文引用:1]
[3]	崔孝秉, 张宏, 宋治. 套管柱稳定性问题研究[J]. 石油学报, 1998, 19(1): 124-128. Cui Xiao-bing, Zhang Hong, Song Zhi. A research on casing string stability of oilwell[J]. Acta Petrolei Sinica, 1998, 19(1): 124-128. [本文引用:2]
[4]	焦永树, 蔡宗熙, 严宗达. 铅垂井段钻柱在浮重作用下的静力分岔分析[J]. 工程力学, 1998(增刊), 256-260. Jiao Yong-shu, Cai Zong-xi, Yan Zong-da. The static bifurcation analysis of drillstring in vertical wells under the effect of floating heavy[J]. Engineering Mechanics, 1998(Sup. ): 256-260. [本文引用:1]
[5]	于永南, 胡玉林, 韩志勇, 等. 井眼中钻柱稳定性分析的有限元法[J]. 石油大学学报: 自然科学版, 1998, 22(6): 77-81. Yu Yong-nan, Hu Yu-lin, Han Zhi-yong, et al. Analysis of drillstring stability in wellbore by using finite element method[J]. Journal of the University of Petroleum (Edition of National Science), 1998, 22(6): 74-78. [本文引用:1]
[6]	高国华, 李琪, 张健仁. 管柱在垂直井眼中的屈曲分析[J]. 西安石油学院学报: 自然科学版, 1996, 11(1): 33-35. Gao Guo-hua, Li Qi, Zhang Jian-ren. Buckling analysis of pipe string in a vertical bore hole[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 1996, 11(1): 33-35. [本文引用:2]
[7]	谈梅兰, 甘立飞, 王鑫伟. 斜直井内钻柱的非线性螺旋屈曲[J]. 工程力学, 2007(增刊2): 199-202. Tan Mei-lan, Gan Li-fei, Wang Xin-wei. Nonlinear helical buckling of drillstring in inclined wellbore[J]. Engineering Mechanics, 2007(Sup. 2): 199-202. [本文引用:2]
[8]	刘凤梧, 徐秉业, 高德利. 封隔器对油管螺旋屈曲的影响分析[J]. 清华大学学报: 自然科学版, 1999, 39(8): 105-108. Liu Feng-wu, Xu Bing-ye, Gao De-li. Packer effect analysis of helical buckling of well tubing[J]. Journal of Tsinghua University (Science &Technology), 1999, 39(8): 105-108. [本文引用:2]
[9]	刘峰, 王鑫伟. 直井中钻柱非线性屈曲的DQ法分析[J]. 吉林大学学报: 工学版, 2007, 37(1): 234-238. Liu Feng, Wang Xin-wei. Differential quadrature method for nonlinear buckling analysis of tubing in straight wells[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(1): 234-238. [本文引用:2]
[10]	Lubinski A, Althouse W S. Helical buckling of tubing sealed in packers[J]. Journal of Pertoleum Technology, 1962, 14(6): 655-670. [本文引用:2]
[11]	Jr Cheatham J B. Helical postbuckling configuration of a weightless column under the action of axial Load[J]. SPE Society of Petroleum Engineers, 1984, 24(2): 467-472. [本文引用:2]
[12]	Mitchell R F. Buckling behavior of well tubing: the packer effect[J]. Society of Petroleum Engineers Journal, 1982, 22(5): 616-624. [本文引用:2]
[13]	Mitchell R F. Effect of well deviation on helical buckling[J]. SPE Drillling and Completion, 1997, 46(3): 63-69. [本文引用:2]
[14]	Mitchell R F. Helical buckling of pipe with connectors in vertical wells[J]. SPE Drillling and Completion, 2000, 15(3): 162-166. [本文引用:2]
[15]	Mitchell R F. New concepts for helical buckling[J]. SPE Drilling Engineering, 1988, 3(3): 303-310. [本文引用:2]
[16]	Sorenson K G, Cheatham J B. Post-buckling behavior of a circular rod constrained within a circular cylinder[J]. Journal of Applied Mechanics, 1986, 53(4): 929-934. [本文引用:2]
[17]	黄文君, 高德利, 魏绍蕾. 边界条件对无重管柱螺旋屈曲的影响分析[J]. 西安石油大学学报: 自然科学版, 2015, 30(3): 87-94, 11. Huang Wen-jun, Gao De-li, Wei Shao-lei. Effects of boundary conditions on helical buckling of weightless tubular string[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2015, 30(3): 87-94, 11. [本文引用:2]
[18]	Huang W J, Gao D L, Wei S L, et al. Boundary conditions: a key factor in tubular-string buckling[J]. SPE Society of Petroleum Engineers, 2015, 20(6): 409-420. [本文引用:2]
[19]	Huang Wen-jun, Gao De-li, Liu Ying-hua. A study of tubular string buckling in vertical wells[J]. International Journal of Mechanical Sciences, 2016, 118: 231-253. [本文引用:3]

2003

0.0

. 2003, 24(4):108-112 DOI:doi:10.3321/j.issn:0253-2697.2003.04.025

Mechanical analysis on causes of worn rod string and tubing of rod pumping wells in the water-flooding oilfield

水驱抽油机井杆管偏磨原因的力学分析

Dong Shi-min

董世民

建立了铅垂油井杆管偏磨临界轴向压力的计算公式.杆管偏磨的临界轴向压力只取决于抽油杆直径与轴向分布力;应用波动方程建立了抽油杆柱轴向分布力的模拟方法;建立了供液不足油井液击力的计算公式,改进了柱塞下行阻力的计算方法.系统分析了油井生产条件与生产参数对杆管偏磨的临界轴向压力与柱塞下行阻力的影响.分析结果表明:(1)含水与沉没度对杆管偏磨有显著影响,高含水油井在低沉没度下运行会明显降低杆管偏磨的临界轴向压力;(2)当油井供液不足时,柱塞下冲程时泵内将产生液击,并加大柱塞下行阻力;(3)抽汲参数增加不仅导致抽油杆柱振动加剧,降低了杆管偏磨的临界轴向压力,而且也加大了柱塞下行阻力.当抽油杆柱在上述一个或几个条件共同作用下达到偏磨临界条件时,杆管将产生偏磨.

... 抽油杆柱在油管内屈曲临界载荷和构型的分析计算方法是直井抽油机井杆管偏磨分析的理论基础^[1] ...

... 研究结果表明,细长杆柱在铅直圆筒内的屈曲构型分为两类:轴向压力较小时的平面屈曲构型^[1,2,3,4,5] ...

1950

0.0

... 研究结果表明,细长杆柱在铅直圆筒内的屈曲构型分为两类:轴向压力较小时的平面屈曲构型^[1,2,3,4,5] ...

1998

0.0

. 1998, 19(1):124-128

A research on casing string stability of oilwell

套管柱稳定性问题研究

Cui Xiao-bing , Zhang Hong , Song Zhi

崔孝秉, 张宏, 宋治

... 研究结果表明,细长杆柱在铅直圆筒内的屈曲构型分为两类:轴向压力较小时的平面屈曲构型^[1,2,3,4,5] ...

... 用极坐标 θ表示的螺旋屈曲段杆柱弯曲微分方程、杆柱与油管之间接触力方程分别为^[3]: ...

1998

0.0

. 1998, (增刊):256-260

The static bifurcation analysis of drillstring in vertical wells under the effect of floating heavy

铅垂井段钻柱在浮重作用下的静力分岔分析

Jiao Yong-shu , Cai Zong-xi , Yan Zong-da

焦永树, 蔡宗熙, 严宗达

以往研究钻柱静力稳定性的文献大都忽略了轴力沿轴线变化而产生的影响,因而得出的结果与实际情况有一定差距。本文在考虑几何非线性和轴力沿轴线变化的基础上,研究了铅垂井段钻柱在浮重作用下的静力分岔行为,得到了钻柱发生静力分岔的前六阶分岔值及相应的分岔解。由此,我们不仅可以得到钻柱发生静力分岔时的临界钻压和临界长度,而且还可以根据分岔解为钻井工程中稳定器和弯接头的安装提供参考位置。

... 研究结果表明,细长杆柱在铅直圆筒内的屈曲构型分为两类:轴向压力较小时的平面屈曲构型^[1,2,3,4,5] ...

1998

0.0

. 1998, 22(6):77-81

Analysis of drillstring stability in wellbore by using finite element method

井眼中钻柱稳定性分析的有限元法

Yu Yong-nan , Hu Yu-lin , Han Zhi-yong

于永南, 胡玉林, 韩志勇

... 研究结果表明,细长杆柱在铅直圆筒内的屈曲构型分为两类:轴向压力较小时的平面屈曲构型^[1,2,3,4,5] ...

1996

0.0

. 1996, 11(1):33-35

Buckling analysis of pipe string in a vertical bore hole

管柱在垂直井眼中的屈曲分析

Gao Guo-hua , Li Qi , Zhang Jian-ren

高国华, 李琪, 张健仁

... 轴向压力较大时的空间屈曲构型^[6,7,8,9] ...

... 当考虑边界条件的影响时,细长杆柱在铅直圆筒内的空间屈曲构型可由三段、四段或五段组成^[6,7,8,9]:底部空间梁段(1或2段)、中间螺旋段、顶部空间梁段(1或2段) ...

0.0

. , 2007(增刊2):199-202 DOI:doi:10.3969/j.issn.1000-4750.2007.z2.023

Nonlinear helical buckling of drillstring in inclined wellbore

斜直井内钻柱的非线性螺旋屈曲

Tan Mei-lan , Gan Li-fei , Wang Xin-wei

谈梅兰, 甘立飞, 王鑫伟

基于最小位能原理,研究了斜直井内钻柱的非线性螺旋屈曲问题.利用圆柱面坐标系,使接触非线性问题简化成了纯几何非线性问题.对于上端周向自由,下端铰支的钻柱,用Rayleigh-Ritz法得到了有一定横向载荷作用时,确定螺旋屈曲临界载荷无量纲形式的非线性积分方程.应用符号运算软件Maple10,对具体的工程算例进行了求解.研究发现:该文的计算结果与已有的实验结果吻合,说明钻柱的螺旋屈曲问题是非线性问题,同时也证实了该文的非线性算法的有效性.该方法可用于求解斜直井内的钻柱屈曲问题.

... 轴向压力较大时的空间屈曲构型^[6,7,8,9] ...

1999

0.0

. 1999, 39(8):105-108 DOI:doi:10.3321/j.issn:1000-0054.1999.08.027

Packer effect analysis of helical buckling of well tubing

封隔器对油管螺旋屈曲的影响分析

Liu Feng-wu , Xu Bing-ye , Gao De-li

刘凤梧, 徐秉业, 高德利

油管的螺旋屈曲对封隔器有严重的影响.本文将管柱分为在封隔器附近的空间梁柱段和与约束管壁连续接触的屈曲构形段,通过、分析求解管柱屈曲后所满足的四阶强非线性常微分方程,考虑管柱的固支端部边界条件和连续条件,得到了屈曲管柱变形的解析解.进而得到了管柱在封隔器附近的内力等.所得解析结果与Sorenson的数值结果一致.

... 轴向压力较大时的空间屈曲构型^[6,7,8,9] ...

2007

0.0

. 2007, 37(1):234-238

Differential quadrature method for nonlinear buckling analysis of tubing in straight wells

直井中钻柱非线性屈曲的DQ法分析

Liu Feng , Wang Xin-wei

刘峰, 王鑫伟

... 轴向压力较大时的空间屈曲构型^[6,7,8,9] ...

1962

0.0

... 文献[10,11,12,13,14,15,16,17,18,19]以底部空间梁段与中间螺旋段杆柱为研究对象,建立了空间梁段与中间螺旋段杆柱的弯曲微分方程,并考虑了边界条件以及空间梁段与中间螺旋段弯曲变形的连续性条件,建立了底部空间梁段与中间螺旋段构型仿真的数学模型,但没有严格基于数学方法建立系统的数值仿真模型,而是基于假设和简化对中间螺旋段的四阶弯曲常微分方程进行了降阶处理,计算结果仅仅讨论了边界条件对底部空间梁段长度的影响,没有反映出边界条件对螺旋屈曲构型的影响 ...

... 3 与简化模型结果对比目前,学者对杆柱空间屈曲进行的研究都是将螺旋段复杂的非线性微分方程进行简化处理而得到的近似结果^{[10,11,12,13,14,15,16,17,18,19]},与实际有较大出入 ...

1984

0.0

1982

0.0

1997

0.0

2000

0.0

1988

0.0

1986

0.0

2015

0.0

. 2015, 30(3):87-94,11

Effects of boundary conditions on helical buckling of weightless tubular string

边界条件对无重管柱螺旋屈曲的影响分析

Huang Wen-jun , Gao De-li , Wei Shao-lei

黄文君, 高德利, 魏绍蕾

2015

0.0

2016

0.0

... 表2和图9分别给出了本文完整模型和文献[19]简化模型的对比结果 ...