中国道路交通事故统计年报数据^[1]显示:2012年全国发生道路交通事故204 196起, 造成59 997人死亡、224 327人受伤, 直接财产损失达11.75亿人民币。为提高汽车安全性, 假人广泛应用于汽车碰撞安全检测。研究表明^{[2, 3]}, 车辆交通事故造成的人员死亡中, 30%是由胸部损伤导致, 且在所有车辆交通事故导致的乘员致命和严重伤害中, 胸部损伤位居第二, 仅次于头部损伤。因此假人胸部损伤指标在C-NCAP^[4]星级评分中占有最大分值比重。

假人胸部设计比较复杂, 较难通过标定试验。故采用仿真对假人胸部力学特性进行研究, 对提高模型准确度、提升汽车安全性能、指导汽车设计至关重要。商恩义等^[5]针对偏置碰撞试验提出了“ 合力与合外力” 的方法。Forman等^[6]研究了假人胸部在低速正面碰撞下的力学特性, 并对比分析了胸部位移在不同速度下的变化。Mizuno等^[7]分析了不同约束条件对假人胸部位移与加速度的影响。随着商用仿真假人版本升级, 细化的网格虽然提升了仿真程度, 但是计算时间巨幅增加, 对注重分析效率的实际工程应用提出了极大的挑战。开发有限元仿真假人必须通过标定试验。而假人胸部位移量峰值 Dmax和胸部摆锤力峰值 Fmax是评价假人胸部力学特性的两个主要标准, 假人胸部模型开发涉及多目标优化问题。

在实际工程结构多目标优化问题中, 诸如粒子群等智能优化算法应用广泛^{[8, 9]}。但这些方法有时搜索速度较慢、优化效率较低。目前, 处理多目标优化问题的一种有效策略是将多目标问题等效标量化处理, 采用数学优化算法求解。Geoffrion^[10]提出的加权和法, 由于思路简单、易于与其他方法组合构建出快速求解的优化算法而得到广泛应用。近年来, 人们将加权和法与求解优化问题的牛顿法、拟牛顿法等相结合, 陆续设计出求解多目标优化问题的数值算法^{[11, 12]}。

本研究基于结构材料灵敏度分析, 提出了大量精简有限元网格剖分单元及节点的混合单元策略, 建立了简化有效的假人胸部有限元仿真模型。为提高该简化模型的 “ 拟人” 程度, 设计了对应的多目标优化模型。进而, 构建了基于加权和法的快速多目标优化MBNWS算法, 并应用于胸部简化模型优化设计, 获得了其Pareto最优解及前端。

以Hybrid III V5.0有限元假人胸部结构为参考, 运用人体损伤生物力学原理, 借鉴力学原理中结构等效的思想, 对有限元假人胸部进行结构设计, 力求在不降低仿真精度的前提下, 使胸部结构模型更加简洁, 以提升实际工程应用效率, 同时指导有限元假人的整体结构设计。

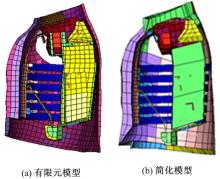
有限元假人胸部结构模型相对固定, 胸部的力学特性主要与各组织结构的材料属性参数密切相关。基于结构材料灵敏度分析方法, 探讨了在受到正面冲击时, 现有有限元胸部各组织结构的传力情况及其对应参数变化对胸部损伤的影响, 确定了各结构材料参数对胸部力学特性的敏感程度。在此基础上, 对胸部有限元模型进行简化设计, 得到其简化模型, 如图1(b)所示, 图1(a)为现有假人胸部有限元模型。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 假人胸部的有限元模型Fig.1 Finite element models of dummy chest

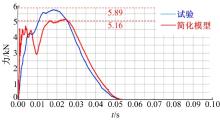
针对简化模型进行标定试验验证, 得到胸部位移量和胸部摆锤力随时间的变化情况, 如图2、3的红色曲线所示, 蓝色曲线为对应的物理假人试验曲线。简化模型曲线与物理假人曲线变化趋势相同, 峰值满足标定要求, 表明简化模型完全有效。对比Hybrid III 50^th假人胸部模型, 本文获得的简化模型有限元剖分网格的单元数、节点数与组件数大幅下降, 对比结果如表1所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 胸部位移-时间曲线Fig.2 Chest displacement-time curve

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 胸部摆锤力-时间曲线Fig.3 Chest force-time curves

表1

Table 1

表1(Table 1)

表1 简化胸部模型的单元数、节点数与组件数 Table 1 Number of units, nodes and components of simplified chest model 单元数 节点数 组件数 有限元模型(V5.0) 18682 13928 67 简化模型 10898 9057 56 下降百分比/% 41.7 35 16.4

表1 简化胸部模型的单元数、节点数与组件数 Table 1 Number of units, nodes and components of simplified chest model

汽车正碰有限元假人胸部标定试验关注的是胸部位移量和摆锤力曲线是否尽可能与物理假人试验结果保持高度一致。为进一步提高简化模型的精确度, 可基于材料参数对假人胸部的简化结构进行多目标优化设计。

为了快速、准确地求解假人胸部结构多目标优化问题, 本文构建了基于加权和法与BFGS拟牛顿算法求解不等式约束多目标优化问题的快速算法。不等式约束多目标优化可用问题(4)描述:

minf(x), x∈Ds.t.ci(x)≥0, i=1, 2, …, r(4)

式中: x=(x1, x2, …, xn)T为设计变量, n是变量个数; f(x)=(f1(x), f2(x), …, fl(x))T∈Rl是优化目标函数向量, l是分量函数的个数; D={x∈Rn/li≤xi≤ui}是可行域; li、ui分别为其下上值; ci(x), i=1, 2, …, r为不等式约束函数。

一般地, 多目标优化问题(4)的解, 可采用帕累托(Pareto)最优解集^[11]描述, 与之对应的优化目标函数值, 则组成了Pareto最优前端。在优化设计问题中, Pareto最优解集对应了优化后的设计方案参数集合; 而Pareto最优前端可清晰地给出优化后的目标性能指标参数集合, 供设计者参考。

3.3 求解多目标优化的MBNWS算法

对于求解无约束单目标优化问题(7), 很有效的方法是拟牛顿法中的BFGS算法。为了确保该算法中的近似迭代矩阵 Bk满足对称正定传递, 选取一种修正BFGS拟牛顿算法^[15], 简称M-BFGS优化算法, 求解问题(7)的执行步骤如下:

Step1 选择初始向量 x0∈Rn,及初始对称正定矩阵 B0∈Rn×n;常数 0< σ1< 1, α> 0, ε> 0, k:=0。

Step2 判断条件 gk≤ε是否满足, 满足则停止; 否则转Step3。

Step3 计算搜索方向 dk=-Bk-1gk。

Step4 通过求解不等式(8)获取搜索步长 αk。

G(xk+αkdk)≤G(xk)+σ1αkgTkdk(8)

Step5 迭代矩阵 Bk+1为:

Bk+1=Bk-BksksTkBksTkBksk+ykyTkyTksk, 若sTkyk> 0; Bk, 其他;

Step6 令 xk+1=xk+αkdk。

Step7 令 k:=k+1转向Step1。

其中: gk=∇G(xk)是函数 G(x)在 xk处的梯度向量; sk=xk+1-xk, yk=∇G(xk+1)-∇G(xk)。

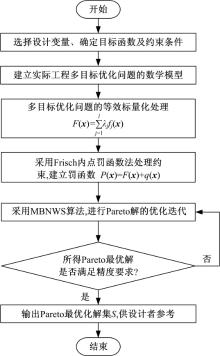
归纳总结3.1~3.3节, 设计了一种求解不等式约束多目标优化问题(4)的新算法, 简称为MBNWS算法。该算法的优势是:将多目标问题等效标量化; 将有约束惩罚转化为无约束; 利用了BFGS算法高阶收敛性, 所以可以快速、有效地求解多目标优化问题, MBNWS算法流程如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 MBNWS算法的优化流程图Fig.5 Flow chart of MBNWS algorithm

针对2.1节建立的假人胸部简化模型的多目标优化问题(1), 将其优化目标的代理函数(2)(3)代入, 并分别进行归一化预处理; 约束条件取为试验标定可行域, 问题(1)的等价形式便为不等约束多目标优化问题(9)。利用3.3节设计的MBNWS优化算法对假人胸部结构的材料参数进行多目标优化, 以便获得最优化设计方案。

minF1(x)=D'max(x)D0, F2(x)=F'max(x)F0s.t.0.399≤x1≤0.7480.049≤x2≤0.0930.175≤x3≤0.325(9)

应用MBNWS算法求解多目标优化问题(9)的步骤如下:

(1)利用加权和法对问题(9)中目标函数等效标量化处理得和函数如下:

F(x)=λ1F1(x)+λ2F2(x)(10)

式中:权因子 λ1, λ2> 0,且 λ1+λ2=1。

(2)处理约束条件, 取罚函数项;

p(x)=-σ-1∑i=13log[(li+ui)xi-xi2-liui](11)

则问题(1)便可等效转化为如下无约束单目标优化问题:

minG(x)=F(x)+p(x)x∈R3(12)

(3)按照3.3节M-BFGS算法的步骤, 求解无约束优化问题(12)。

通过寻优计算得到多目标问题的Pareto最优解集, 根据胸部力学特性响应结果(Pareto前端)选取参数构成最佳设计方案为:材料的短效剪切模量 G0=0.74、长效剪切模量 G1=0.079与衰减系数 β=0.25。将优化后的结果参数代入假人胸部仿真模型进行对比, 参数峰值对比结果见表2。

表2

Table 2

表2(Table 2)

表2 优化前、后设计变量及性能指标对比 Table 2 Comparison of design variables and performance indicators before and after optimization x=(x1, x2, x3) Dmax/mm Fmax/kN 滞后率 /% G0/MPa G1/MPa β 原设计 0.57 0.0713 0.25 68.85 5.19 69.8 优化后 0.74 0.079 0.25 65.33 5.75 71.9 标定要求 - - - 63.5~72.6 5.16~5.89 69~85 试验 - - - 65.34 5.8 73.98 误差/% - - - -0.015 -0.86 -2.81

表2 优化前、后设计变量及性能指标对比 Table 2 Comparison of design variables and performance indicators before and after optimization

由表2可见, 优化后假人胸部模型的位移量峰值 Dmax和摆锤力峰值 Fmax不仅完全符合标定试验要求, 而且 Dmax降至为65.33 mm, 与物理假人的峰值误差由3.51 mm降低为0.01 mm, 误差下降到-0.015%; Fmax为5.75 kN, 相对物理假人的峰值误差由0.61 kN降低为0.05 kN, 误差下降到-0.86%。

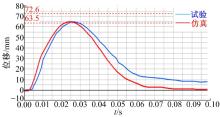
对比优化得到的胸部有限元模型的仿真实验与物理假人标定试验的胸部位移-时间曲线和摆锤力-时间曲线, 分别如图6和图7所示, 红色为仿真假人曲线, 蓝色为物理假人试验曲线。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 优化后胸部位移-时间曲线Fig.6 Chest displacement-time curve after optimization

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 优化后胸部摆锤力-时间曲线Fig.7 Chest force-time curve after optimization

比较图 6的曲线可以看出:在0~0.1 s之间, 仿真模型的胸部位移量随时间的变化趋势与试验结果基本一致, 并且在0~0.035 s时, 两条曲线非常接近, 在0.025 s时均达到了位移量的最大值。比较图7的曲线可知, 在0.01~0.05 s时, 两条曲线基本重合, 两者几乎同时达到了摆锤力峰值, 曲线显示两点基本重合, 说明仿真结果与试验结果高度拟合。综合表2、图6与图7可知:与优化前的模型相比, 优化后的模型精度更高, 能够更加准确地模拟实际碰撞试验中假人胸部结构的力学响应特性, 可为乘员安全设计提供参考。

为了提高对碰撞假人胸部力学特性的分析效率, 本文建立了满足标定试验要求的假人胸部等效简化有限元模型。致使简化后模型的单元数降低了41.7%, 节点数与组件数分别降低了35% 和16.4%, 大大提高了计算效率。为了获得更高精度的假人胸部模型, 取其胸部位移量峰值D_max与摆锤力峰值F_max作为假人胸部力学特性的主要性能指标, 胸部肋骨结构的材料参数作为设计变量, 建立了多目标优化模型。设计了MBNWS多目标优化算法, 进行其优化设计, 快速获得了优化方案。优化后的假人胸部简化模型的整体标定曲线、峰值及峰值时刻都与物理假人非常吻合。其中, 胸部位移量峰值仅有-0.015%的误差, 摆锤力峰值也仅有-0.86%的误差。与原始设计相比, 该优化模型能够更加准确地模拟物理假人碰撞过程中人体胸部受到的伤害, 为乘员安全设计提供了设计思路。同时, 所建立的优化算法在基于材料参数设计的假人胸部结构多目标优化问题中表现出的优秀性能, 为该算法用于求解其他工程多目标优化问题, 缩短设计周期提供了实践证明。