拉伸试样选用3种典型金属材料:低碳钢合金的化学成分为:w(C)=0.067%, w(Mn)=0.346%, w(Si)=0.054%, w(S)=0.013%, w(P)=0.021%, w(Cu)=0.01%, w(Ti)=0.002%, 其余为Fe; 黄铜合金(H62)的化学成分为:w(Cu)=0.62%, w(Fe)=0.15%, w(Pb)=0.08%, w(Sb)=0.005%, w(Bi)=0.002%, w(P)=0.01%, w(Zn)=0.37%; 硬铝合金(LY12)的化学成分为:w(Cu)=4.0%, w(Mg)=1.6%, w(Si)=0.5%, w(Mn)=0.6%, w(Fe)=0.5%, w(Ni)=0.5%, w(Cr)=0.1%, 其余为Al。其中低碳钢为便于后续数据处理分析, 在制作试样前对材料作加工硬化处理, 以消除试验曲线的屈服平台。

单向拉伸试验在电子万能材料试验机(WQ4100)上进行, 参照金属材料常温拉伸试验国家标准《GB /T 228— 2002》^[13]。试样标距长度和直径分别为50 mm和10 mm。试样装夹在试验机夹具之间, 试样承受的拉伸载荷由试验机力传感器记录, 力传感器量程100 kN, 精度为0.5级, 试样标距范围轴向变形由装夹于试样上电子引伸计(Y50/20-N)记录, 其标距为50 mm, 量程为20 mm, 精度为0.5级。试样标距范围内颈缩图像由自行研制的光学测量装置记录, 光学测量装置主要包括CCD工业相机(DH-HV1302UC-T)并配置变焦镜头(Computar MLM-3XMP)、LED 光源、三角架固定平台、安装有图像采集软件的电脑以及Halcon处理软件, CCD工业相机分辨率为1280× 1024 pixel, 图像采集频率为15帧/s。工业相机镜头正对试样标距部位, 两者直线距离约为35 cm, 镜头轴线与试样轴线相互垂直, 并正交于试样标距中点。电脑连接相机采集试样图像信息, 经Halcon软件处理得到试样几何轮廓坐标数据。试验前对光学测量装置得到的坐标信息进行系统标定, 试验后利用引伸计数据对比验证光学测量装置测定的试样轮廓坐标, 并进行适当修正。经反复调试, 光学测量装置的测量精度约为± 0.05 mm。图1显示了低碳钢试样变形量为7.229 mm时呈现颈缩特征的光学图像, 相应地经Halcon软件编程处理并导入Origin软件生成试样标距部分几何轮廓坐标曲线如图2所示。经Origin软件数据处理, 可以得到试样颈缩处的最小径向半径a和外轮廓曲率半径R。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 Halcon处理后的拉伸试样图像(低碳钢)Fig.1 Necking image of tension specimen processed by Halcon(mild steel)

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 拉伸试样颈缩轮廓图Fig.2 Necking contour curve of tension specimen

3种金属材料的拉伸载荷-变形曲线如图3所示, 相应的力学性能参数测量结果分别列于表1~表3, 其中应变硬化指数n求取过程参照《GB /T 5028— 2008》^[14]。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 拉伸试验载荷-变形曲线Fig.3 Load vs. displacement curves of tension test

表1

Table 1

表1(Table 1)

表1 低碳钢力学性能 Table 1 Mechanical properties of mild steel 试验 屈服强度 /MPa 极限强度 / MPa 应变硬 化指数 有效应 变范围 拉伸 470 715 0.11 0~1.0 扭转 430 610 0.07 0~1.6

表1 低碳钢力学性能 Table 1 Mechanical properties of mild steel

表2

Table 2

表2(Table 2)

表2 H62合金力学性能 Table 2 Mechanical properties of H62 alloy 试验 屈服强度 /MPa 极限强度 / MPa 应变硬 化指数 有效应 变范围 拉伸 240 700 0.31 0~0.6 扭转 270 575 0.25 0~0.76

表2 H62合金力学性能 Table 2 Mechanical properties of H62 alloy

表3

Table 3

表3(Table 3)

表3 硬铝合金力学性能 Table 3 Mechanical properties of LY12 alloy 试验 屈服强度 /MPa 极限强度 / MPa 应变硬 化指数 有效应 变范围 拉伸 385 620 0.20 0~0.12 扭转 325 545 0.18 0~0.7

表3 硬铝合金力学性能 Table 3 Mechanical properties of LY12 alloy

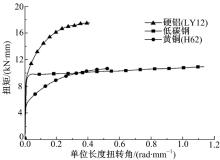
扭转试验在扭转试验机(NZ-10)上进行, 参照金属材料室温扭转方法《GB/T 10128— 2007》^[15], 圆棒试样标距长度为20 mm, 低碳钢和H62试样标距直径均为5 mm, LY12试样标距直径为6 mm。试样装夹在上下两夹持端, 其中下夹持端传递扭矩, 上夹持端固定, 但在轴向上保持自由度, 确保试样在扭转中始终处于纯剪应力。扭矩由与上夹持端固接的力矩传感器记录, 力矩传感器量程为20 N· m, 精度为0.5级, 扭转角由与下夹持端同轴安装的编码器记录。3种金属材料扭矩-单位长度扭转角曲线如图4所示, 相应的力学性能参数测量结果分别列于表1~表3。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 扭矩-单位长度扭转角曲线Fig.4 Torque vs. twist angle per unit length curves of torsion test

基于力学基础理论, 可将以上测得的试验数据转换为硬化曲线。

(1)拉伸试验获得的真应力-真应变曲线

在拉伸载荷最大点之前, 采用以下公式计算真应力-真应变曲线:

σ=s1+e(1)

ε=ln1+e(2)

式中: σ、ε分别为真应力和真应变; e、s分别为工程应力和工程应变。

在载荷最大点之后, 试样在颈缩部位局部变形, 颈缩部位承受三向拉应力。根据Bridgman法^[2], 通过试样颈缩几何参数求解颈缩最小径处的等效应力和等效应变, 其计算公式如下:

σeq=Fπa21+2Raln1+a2R(3)

εeq=2lna0a(4)

式中: σeq和 εeq分别为等效应力和等效应变; F为拉伸载荷; a₀为试样原始半径; a为颈缩最小径处的径向半径; R为试样颈缩外轮廓在颈缩最小径处的曲率半径。

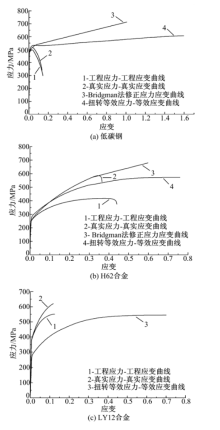
图5显示了低碳钢、H62和LY12合金的真实应力-真实应变硬化曲线以及工程应力-工程应变曲线。其中, 工程应力-工程应变曲线如图5的曲线1所示, 工程应力-工程应变曲线经式(1)(2)计算转换的真实应力-真实应变硬化曲线如图5的曲线2所示, 低碳钢和H62合金拉伸载荷-变形试验曲线经Bridgman法计算的真实应力-真实应变硬化曲线如图5(a)(b)的曲线3所示, 而LY12合金没有明显颈缩现象, 无法应用Bridgman法计算硬化曲线。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 低碳钢、H62和LY12合金拉伸和扭转应力应变曲线比较Fig.5 Comparisons of stress vs. strain curves between tension and torsion of mild steel, H62 alloy and LY12 alloy

(2)扭转试验获得的真实应力-真实应变曲线根据Nadai分析^[1], 首先假定扭转变形过程中试样遵从“ 平面假设” 且横截面形状尺寸始终保持不变以及试样轴向无伸缩, 则试样表面最大剪应力和最大剪应变可用如下公式计算:

γ=rθ'(5)

τa=12πa3θ'dMTdθ'+3MT(6)

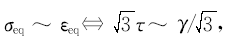式中: θ'为试样单位长度的扭转角; a为圆棒试样半径; MT为扭矩。通过微分运算, 可将扭转试验的扭矩-转角( MT⁃θ)曲线转换为剪应力-剪应变曲线, 再根据 将剪应力-剪应变曲线转换为等效应力-等效应变曲线, 低碳钢、H62和LY12合金扭转试验获取的硬化曲线分别对应于图5(a)(b)的曲线4以及图5(c)的曲线3。

金属塑性成形应变范围与材料变形过程中的力学稳定性密切相关, 并最终取决于材料本身在既定应力状态下的断裂机制^[16]。力学稳定性保证材料最大程度地均匀变形, 抑制局部化变形, 从而避免材料过早断裂, 因此直接决定着拉伸或扭转试验可测量的有效应变范围。材料在拉伸和扭转载荷下的塑性流动力学稳定性各不相同。在拉伸过程中, 试样横截面不断减缩, 在拉伸载荷最大点之前, 材料本身应变硬化能力补偿了横截面减缩造成的几何软化, 试样整体是均匀变形的, 在载荷最大点之后, 材料应变硬化能力不足以平衡横截面减缩造成的几何软化, 材料变形就会局部发展, 形成颈缩。常规手段可测量有效应变范围限制在失稳前拉伸试样经历的均匀应变。而在扭转过程中, 试样在断裂前几何形状几乎不发生变化, 不存在几何软化问题, 试样整体能获得直至断裂的均匀应变。因此, 由于力学稳定性方面的优势, 金属棒材在扭转状态下的均匀应变范围要大于拉伸状态下所经历的均匀应变范围, 这也被本文3种不同金属材料的试验结果所证实, 低碳钢材料扭转均匀应变范围(0~1.6)为拉伸均匀应变范围(0~0.033)的48倍; H62合金扭转均匀应变范围(0~0.76)为拉伸均匀应变范围(0~0.32)的2.3倍; LY12合金扭转均匀应变范围(0~0.70)为拉伸均匀应变范围(0~0.12)的5.8倍。

在拉伸变形失稳后试样要经历一段局部颈缩变形, 颈缩逐渐集中直至断裂。Bridgman方法就是用于进一步拓展拉伸失稳后直至断裂前的应变范围。在扭转变形失稳后试样由表及里迅速断裂, 扭转过程基本上为均匀变形。根据试验结果, 低碳钢、H62合金和LY12合金在扭转断裂前应变分别为拉伸断裂前应变的1.6倍、1.27倍和5.8倍, 因此材料在扭转断裂前经历的应变要普遍大于拉伸断裂前经历的应变。这可能与材料在不同应力状态下断裂机制有关。

通过考察图6所示3种不同延性金属拉伸断口宏观形貌照片可以发现, 塑性很好的低碳钢试样断口呈典型的“ 杯锥” 状, “ 杯口” 环形断面相对光滑, 与试样轴线呈 45° , 属剪切破坏的断裂机制, “ 杯底” 断面粗糙不平, 属拉断破坏的断裂机制。由于“ 杯底” 占绝大部分比例, 所以低碳钢主要是拉断破坏的断裂机制。而塑性稍差的H62合金和塑性更差的LY12合金拉伸试样均没有“ 杯锥” 状断口形貌, 且断面粗糙不平, 都属拉断破坏的断裂机制。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 拉伸断口宏观形貌比较Fig.6 Comparison of macroscopic fracture morphology under tension

扭转断口宏观形貌如图7所示, 3种金属扭转断面均光滑平整, 且与试样轴线垂直, 属于剪切破坏的断裂机理^[17]。根据联合强度理论^[18], 韧性金属在拉伸状态下主要为拉断破坏机制, 受最大拉应力 σmax的极限值控制, 在扭转状态下为剪断破坏机制, 受最大剪应力τ _max的极限值控制, 相应的拉伸和扭转应力状态关系如图8所示。正常情况下, 材料在拉伸状态下会促进其内部孔洞等缺陷发展, 尤其是在颈缩出现后三轴拉应力作用逐渐显著, 材料内部缺陷加速发展, 同时其三轴应力状态比单向拉应力状态更趋于最大拉应力 σmax的极限值(如图8中拉伸应力状态的斜率变化), 从而导致材料加速破坏断裂。而在扭转过程中, 材料在剪应力状态下其内部孔洞等缺陷体积变化不明显, 仅形状和扩展方向发生改变(旋转、扭曲), 经逐渐累积后引起损伤失效, 但失效过程比拉伸变形的破坏过程要缓慢很多, 材料扭转达到最大剪应力τ _max极限值所对应的应变要大于拉伸变形达到最大拉应力 σmax极限值所对应的应变。因此, 同一材料扭转断裂前经历的应变范围要普遍大于拉伸断裂前经历的应变范围, 这源于不同应力状态下断裂机制的差异。与此相对应, 扭转试验的应变测量范围要大于拉伸试验Bridgman法的应变测量范围。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 扭转断口宏观形貌比较Fig.7 Comparison of macroscopic fracture morphology under torsion

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 拉伸和扭转的力学状态对比图Fig.8 Comparison of mechanical state between tension and torsion

另外, 以上3种不同金属材料在拉伸过程中呈现不同的颈缩形态。低碳钢拉伸试样具有明显的集中性颈缩, 其断裂延伸率为14%, 但其断裂前应变达到1.0, 为常规拉伸均匀应变(0.033)的30倍, 因此低碳钢试样拉伸应变范围主要集中在局部颈缩阶段。H62合金拉伸试样具有较大的拉伸均匀应变(0.32), 失稳后呈现平缓的扩展性颈缩形态, 其断裂延伸率为42%, 其断裂前应变(0.6)不足常规拉伸均匀应变(0.32)的 2倍, 可见H62合金断裂前颈缩程度相对较小, 试样整体保持似均匀变形。而LY12合金拉伸试样还未达到载荷最大值驻点就发生近似脆性断裂, 其断裂延伸率为12%, 断裂前应变为0.12, 基本没有颈缩现象。Bridgman法具有很大的局限性, 其强烈地依赖于拉伸试样的颈缩程度, 试样颈缩程度越显著, 拉伸断裂前的局部应变就越大, Bridgman法所测量的应变范围就越大。而拉伸试样颈缩的显著程度与材料性能密切相关, 材料应变硬化指数越小, 试样拉伸稳定性就越差, 从而较早地产生颈缩, 同时材料延性越大, 其主导材料断裂的最大拉应力 σmax的极限值就越大, 拉伸断裂前经历的局部应变就越大, 颈缩程度就越显著。因此, Bridgman法适用于延性大且硬化能力弱的金属, 比如本文的低碳钢合金。而相比而言, 扭转试验具有通用性, 适用于不同性能的金属材料, 而且均能获得远远超过Bridgman法的应变测量范围, 对于大变形情况下的材料弹-塑性性能的标定, 可采用扭转试验代替传统的拉伸试验。

根据表1~表3列出的力学性能参数测量结果可以发现, 同一材料在拉伸和扭转状态下呈现的力学性能存在差异。首先是屈服强度(σ _0.2), 反映材料由弹性变形进入塑性屈服状态的难易程度, 低碳钢和LY12合金拉伸状态下屈服强度均高于扭转状态下, 而H62合金扭转状态下屈服强度略高于拉伸状态下; 其次是应变硬化指数, 反映了材料抵抗塑性变形的能力, 低碳钢和H62合金拉伸状态下应变硬化指数均明显大于扭转状态, LY12合金拉伸状态下应变硬化指数(0.20)略高于扭转状态(0.18); 最后是断裂前极限强度, 反映了材料本身的最大承载能力, 低碳钢在拉伸状态下断裂前承受的有效应力(715 MPa)比扭转状态下(610 MPa)要高出17%, H62合金在拉伸状态下断裂前承受的有效应力(700 MPa)比扭转状态下(575 MPa)高出22%, LY12合金在拉伸状态下最大有效应力(620 MPa)比扭转状态下(545 MPa)要高出14%。

以上3种材料实验结果显示, 相比于拉伸状态, 在扭转状态下的金属棒材呈现出不同程度的“ 软化” 现象, 即金属一般在扭转状态下比拉伸状态更易进入塑性屈服状态, 同时抵抗形变的应变硬化能力和极限承载能力均显著减弱。国内外同类型的研究工作也表明^{[19, 20, 21]}, 铝合金、低碳钢和铜合金棒材在扭转状态下与拉伸状态相比也存在着类似的软化现象。El-Danaf和孙朝阳等^{[22, 23]}对AA1056铝合金、MP35N钴镍合金、IF钢、AK钢、70-30铜合金材料和TWIP钢单向压缩和扭转的试验结果进行对比发现, 材料在扭转应力状态与压缩状态相比也呈现出相同的软化现象。由此可见, 这种金属棒材在扭转状态下呈现的软化现象具有普遍性, 这或许由于金属圆棒型材成形工艺导致的材料组织结构的各向异性, 也可能是材料在不同应力状态下呈现的力学普遍规律。但是目前针对这一现象还没有系统的总结归纳工作, 对于这种现象背后的材料或力学本质原因也未引起足够重视, 本文作者将在后续工作进行专门研究, 并由此对拉伸和扭转试验各自的适用情况进行分析。