基于ADAMS的半悬挂式农业机组静侧翻稳定性

引用本文

陈东辉, 吕建华, 龙刚, 张宇晨, 常志勇. 基于ADAMS的半悬挂式农业机组静侧翻稳定性[J].吉林大学学报（工学版）, 2018,48(4): 1176-1183
CHEN Dong-hui, LYU Jian-hua, LONG Gang, ZHANG Yu-chen, CHANG Zhi-yong. Static rollover stability of semi-mounted agricultural machinery based on ADAMS[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 1176-1183 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170751
Permissions

基于ADAMS的半悬挂式农业机组静侧翻稳定性

陈东辉^1,², 吕建华^1,², 龙刚^1,², 张宇晨^1,², 常志勇^1,²

1.吉林大学生物与农业工程学院,长春 130022

2.吉林大学工程仿生教育部重点实验室,长春 130022

通讯作者:常志勇(1980-),男,工程师,博士.研究方向:农业机械化工程.E-mail:zychang@jlu.edu.cn

作者简介:陈东辉(1961-),男,教授,博士.研究方向:农业机械化工程与表面摩擦学.E-mail:dhchen@jlu.edu.cn

基金:国家重点研发计划项目(2016YFD0701102); 吉林省教育厅“十三五”产业化培育项目(吉教科合字[2016]442号); 吉林省教育厅“十三五”科学技术项目(吉教科合字[2016]435号、441号); 吉林大学研究生创新基金项目(2017057).

摘要

针对目前半悬挂式农业机组侧翻稳定性研究的不足,提出了一种新的表征机组静侧翻稳定性的有效方法。以横向载荷转移率(LTR)作为机组的侧翻指标,建立了半悬挂式农业机组的侧翻数学模型并进行了准静态侧翻仿真试验。通过ADAMS动力学建模,得到仿真结果与数学模型高度一致,验证了理论模型的正确性。讨论了半悬挂式农业机组各参数对机组静侧翻稳定性的影响并对影响因素进行了敏感度分析。拖拉机和半悬挂式机具的LTR均与其重心高度、轮距、自身质量、轴距、重心到牵引点的距离及牵引点高度等相关。对侧翻指标各影响因素的敏感度分析表明:拖拉机和半悬挂式机具的重心高度和轮距均为影响其侧翻稳定性的重要因素;若要提高半悬挂式机具的侧翻稳定性,除增大轮距和降低重心高度外,还可采用降低牵引点高度及增大重心到牵引点距离的方法。本研究为半悬挂式农业机组的优化设计提供了理论参考。

关键词: 农业工程; 半悬挂式农业机组; 静侧翻稳定性; 横向载荷转移率; 数学模型; 敏感度分析

中图分类号:S220.1 文献标志码:A 文章编号:1671-5497(2018)04-1176-08

Static rollover stability of semi-mounted agricultural machinery based on ADAMS

CHEN Dong-hui^1,², LYU Jian-hua^1,², LONG Gang^1,², ZHANG Yu-chen^1,², CHANG Zhi-yong^1,²

1.College of Biological and Agricultural Engineering, Jilin University, Changchun 130022,China

2.Key Laboratory of Bionic Engineering, Ministry of Education, Changchun 130022,China

Abstract

To overcome the current deficiency in studying the Rollover Stability (RS) of Semi-mounted Agricultural Machine Unit (SMAMU, including a tractor and semi-mounted machine), a new method to characterize the RS of SMAMU is proposed. The Lateral Load Transfer Ratio (LLTR) is chosen as the evaluation indicator of RS, the rollover mathematical model is established and quasi static simulation is carried out. Through ADAMS dynamic modeling, the simulation results are in good agreement with the mathematical model, which verifies the correctness of the theoretical model. The effects of the parameters of SMAMU on the RS are discussed and the sensitivity of the influencing factors is analyzed. The LLTR is correlated to the height of center of gravity, the wheel-base of the tractor, the weight of the SMAMU, the wheel-center-distance, the distance from the center of gravity to the tow point and the height of tow point. The results show that the height of the center of gravity and the wheel-base of both the tractor and the semi-mounted machine are the important factors affecting the RS. Besides reducing the height of center of gravity or increasing the wheel-base, reducing the height of the tow point or increasing the distance from the center of gravity to the tow point can also improve RS. This work may provide reference for the optimal design of SMAMU.

Keyword: agricultural engineering; agricultural semi-mounted unit; statically lateral roll stability; lateral load transfer ratio (LTR); mathematical model; sensitivity analysis

文章图片

0 引言

农业作业机组的侧翻稳定性是衡量机组安全性能优劣的重要指标之一^[1]。由于半悬挂式挂接方式对于大型、重型及纵向尺寸较长的农业机械具有明显优势, 使其在农业、林业中得到广泛的应用^[2], 但因纵向尺寸长、悬挂点位置高、轮距较窄以及工况环境复杂等因素, 其侧翻稳定性较差, 翻车事故时有发生^{[3, 4]}。解决其固有的稳定性问题是半悬挂式农业机组发展的关键^[5]。

目前, 国内外关于车辆侧翻稳定性的研究大多集中在汽车^{[6, 7, 8]}、重型车辆^[9]和工程车辆^{[10, 11]}等领域。半悬挂式农业机组由拖拉机和半悬挂式机具组成, 其结构与汽车等有很大不同, 且工况环境更为复杂, 其设计研究工作主要针对机组的功能作用、强度分析和结构优化等方面, 在对机组的侧翻稳定性方面鲜有研究。将数学建模分析和动力学仿真应用于车辆静侧翻研究是一种行之有效的方法, 国内外许多学者基于此方法取得了理想的研究成果, Prem等^[12]基于虚拟样机技术进行了车辆的静态侧翻稳定性仿真试验, 并研究了载荷分配对车辆侧翻稳定性的影响; 肖杰等^[13]建立了汽车的静态侧翻模型, 计算得到最大侧翻稳定角, 并且对汽车静态侧翻稳定性的影响因素进行了敏感度分析; 倪菲菲等^[14]建立了车辆行驶过程中的准静态侧翻模型, 推导了侧翻因子的计算公式, 通过仿真方法较全面地分析了汽车侧翻的影响因素。可见, 对于汽车稳定性的研究已经达到了很高的水平^{[15, 16]}, 但是对于半悬挂式农业机组的安全稳定性有待进一步研究。

针对现有半悬挂式农业机组静侧翻稳定性研究的不足, 本文充分研究了国内外车辆静态侧翻稳定性的相关理论^{[17, 18]}, 结合半悬挂式农业作业机组的特殊性, 建立了半悬挂式农业机组的侧翻数学模型和ADAMS动力学模型, 着重分析了机组静侧翻稳定性的影响因素及其敏感度, 进而给出一种表征半悬挂式农业机组静侧翻稳定性的新方法, 为半悬挂式农业机组的优化设计提供了理论参考。

1 半悬挂式农业机组侧翻数学模型的建立

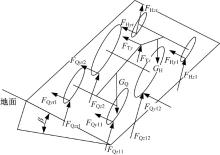半悬挂式农业机组在坡道横向行驶时, 受到重力的作用, 车身附着于坡道并发生倾斜, 受力示意图如图1所示。其中: $F_{Q z l 1} 、 F_{Q z l 2} 、 F_{Q z r 1} 、 F_{Q z r 2}$ 分别为道路对拖拉机左前轮、右前轮、左后轮和右后轮的垂直反力; $F_{Q y l 1} 、 F_{Q y l 2} 、 F_{Q y r 1} 、 F_{Q y r 2}$ 分别为道路对拖拉机左前轮、右前轮、左后轮和右后轮的侧向附着力; $F_{H z l} 、 F_{H z r}$ 分别为道路对半悬挂式机具左轮、右轮的垂直反力; $F_{H y l} 、 F_{H y r}$ 分别为道路对半悬挂式机具左轮、右轮的侧向附着力; $F_{T y} 、 F_{T z}$ 分别为拖拉机对半悬挂式机具的侧向、垂向作用力; $G_{Q}$ 为拖拉机的质量; $G_{H}$ 为半悬挂式机具的质量; $β$ 为试验台横向倾翻角度或者路面的横向坡度角。在模型建立的过程中, 因为轮胎形变量相对较小, 所以可以忽略由于轮胎变形导致的车身重心的变化。

	Figure Option View Download New Window
	图1 半悬挂式农业机组在横向坡道的受力示意图Fig.1 Force schematic diagram of agricultural semi-mounted unit acting on transverse ramp

1.1 拖拉机的侧翻数学模型

对半悬挂式农业机组中的拖拉机建立侧翻数学模型时, 考虑到拖拉机结构的特殊性, 以拖拉机后轴轮距定义拖拉机轮距。并且根据横向载荷转移率的定义^[17], 令: $F_{Q z l 1} + F_{Q z l 2} = F_{Q z l}, F_{Q z r 1} + F_{Q zr 2} = F_{Q z r} 。$

基于图1拖拉机的受力情况建立如下方程:

$F_{Q z l} + F_{Q z r} - F_{Q z} = G_{Q} cosβ$ (1)

$F_{Q y l} + F_{Q y r} - F_{Q y} = G_{Q} sinβ$ (3)

$F_{Q z} = F_{T z} = \frac{b}{a + b} G_{H} cosβ$ (3)

$F_{Q y} = F_{T y} = \frac{b}{a + b} G_{H} sinβ$ (4)

式中:a为半悬挂式机具重心与其牵引点的水平距离; b为半悬挂式机具重心与其轮轴的水平距离。方程(3)中 $F_{Q z}$ 与 $F_{T z}$ 互为相互作用力, 方程(4)中 $F_{Q y}$ 与 $F_{T y}$ 互为相互作用力。

整理方程(1)(2)(3)(4)得:

$F_{Q z l} + F_{Q z r} = G_{Q} cosβ + \frac{b}{a + b} G_{H} cosβ$ (5)

$F_{Q y l} + F_{Q y r} = G_{Q} sinβ + \frac{b}{a + b} G_{H} sinβ$ (6)

式中: $F_{Q y l} = μ F_{Q z l}, F_{Q y r} = μ F_{Q z r},$ 其中 $μ$ 为拖拉机的附着系数。

结合方程(5)(6)可得: $μ = \tan β 。 F_{Q y l} 、 F_{Q y r}$ 需达到拖拉机的附着条件, 若 $μ$ 过小且 $μ < \tan β,$ 拖拉机会沿坡道方向发生侧滑。为保证横向坡度角与机具结构参数这两个变量对拖拉机侧翻稳定性的影响不受侧滑因素干扰, 需满足地面附着系数 $μ$ 足够大的条件, 即 $≫ \tan β 。$

图1中, 根据前文对拖拉机轮距的定义, 本研究假设力 $F_{Q z l}$ 的作用点与力 $F_{Q z l 2}$ 的作用点在同一条直线上且与机组纵轴线平行, 对 $F_{Q z l}$ 列转矩平衡方程可得:

$\begin{array}{l} G_{Q} h_{c 1} \sin β - \frac{B_{1}}{2} G_{Q} cosβ + F_{Q z r} B_{1} + \\ F_{Q y} h_{a} - F_{Q z} \frac{B_{1}}{2} = 0 \end{array}$ (7)

式中: $B_{1}$ 为拖拉机后轴(驱动轮)轮距; $h_{c 1}$ 为拖拉机重心高度; $h_{a}$ 为牵引点高度。联立方程(5)(6)(7)可得:

$F_{Q z r} = \frac{1}{2} F_{Q z} - \frac{h_{a}}{B_{1}} F_{Q y} + \frac{1}{2} G_{Q} cosβ - \frac{G_{Q} h_{c 1} \sin β}{B_{1}}$ (8)

由方程(5)(8)可得:

$F_{Q z l} = \frac{1}{2} F_{Q z} + \frac{h_{a}}{B_{1}} F_{Q y} + \frac{1}{2} G_{Q} cosβ + \frac{G_{Q} h_{c 1} \sin β}{B_{1}}$ (9)

以横向载荷转移率(LTR)作为拖拉机侧翻稳定性的评价指标。定义LTR为左、右轮胎垂向载荷之差与总载荷的比值^[17]:

$LTR = \frac{F_{Q z l} - F_{Q z r}}{F_{Q z l} + F_{Q z r}}$ (10)

将方程(8)(9)代入方程(10)并取绝对值可得:

$LTR = \frac{2 (F_{Q y} h_{a} + G_{Q} h_{c 1} \sin β)}{B_{1} (G_{Q} cosβ + F_{Q z})}$ (11)

将方程(3)(4)代入方程(11), 得到拖拉机的横向载荷转移率(LTR)为:

$LTR = \frac{2 [h_{a} b G_{H} + h_{c 1} G_{Q} (a + b)]}{B_{1} [(a + b) G_{Q} + b G_{H}]} \tan β = K_{1} \tan β$ (12)

式中: $K_{1}$ 为半悬挂式机组中拖拉机的侧翻稳定性系数。

1.2 半悬挂式机具的侧翻数学模型

对图1所示的机组受力状况进行分析可得:

$F_{H z l} + F_{H z r} + F_{T z} = G_{H} cosβ$ (13)

$F_{H y l} + F_{H y r} + F_{T y} = G_{H} sinβ$ (14)

$F_{H y l} b + F_{H y r} b - F_{T y} a = 0$ (15)

$G_{H} cosβb - F_{T z} (a + b) = 0$ (16)

化简上述方程可得:

$F_{H y l} + F_{H y r} = \frac{a}{a + b} G_{H} sinβ$ (17)

$F_{H z l} + F_{H z r} = \frac{a}{a + b} G_{H} cosβ$ (18)

$F_{T y} = \frac{b}{a + b} G_{H} sinβ$ (19)

$F_{T z} = \frac{b}{a + b} G_{H} cosβ$ (20)

假设地面附着系数足够大, 机组不会发生侧滑。则在图1中, 对力 $F_{H z l}$ 的作用点与机组纵轴线平行的轴线取力矩得:

$\begin{array}{l} G_{H} h_{c 2} \sin β - \frac{B_{2}}{2} G_{H} cosβ + F_{H z r} B_{2} - F_{T y} h_{a} + \\ F_{T z} \frac{B_{2}}{2} = 0 \end{array}$ (21)

式中: $B_{2}$ 为半悬挂式机具的轮距; $h_{c 2}$ 为半悬挂式机具重心高度。

将式(19)(20)代入式(21)可得:

$F_{H z r} = \frac{a}{a + b} G_{H} (\frac{1}{2} \cos β - \frac{h_{c 2}}{B_{2}} \sin β)$ (22)

由式(18)(22)可得:

$F_{H z l} = \frac{a}{a + b} G_{H} (\frac{1}{2} \cos β + \frac{h_{c 2}}{B_{2}} \sin β)$ (23)

选取横向载荷转移率LTR的绝对值为侧翻稳定性的评价指标, 则半悬挂式机具的横向载荷转移率可表示为:

$LTR = \frac{F_{H z l} - F_{H z r}}{F_{H z l} + F_{H z r}}$ (24)

将式(22)(23)代入式(24)得半悬挂式机具的横向载荷转移率:

$LTR = \frac{2 h_{c 2}}{B_{2}} \tan β = K_{2} \tan β$ (25)

式中: $K_{2}$ 为半悬挂式机组中半悬挂式机具的侧翻稳定性系数。

2 准静态侧翻仿真试验

2.1 半悬挂式农业机组的简化

半悬挂式农业机组是一个复杂的作业系统, 在进行其静态侧翻稳定性研究时可以忽略一些与之无关的因素从而简化模型, 更高效地实现拖拉机静侧翻稳定性的仿真分析。本研究在仿真建模过程中做出如下简化:

(1)忽略拖拉机的具体构件, 将其简化为摆动前桥和拖拉机机身两部分, 两者通过摇摆销轴连接。

(2)忽略半悬挂式机具上的具体组成部件, 将半悬挂式机具简化为一个刚体。

(3)简化拖拉机与半悬挂式机具之间牵引装置的具体连接形式, 根据半悬挂式机组的牵引特点, 可将其等同为三自由度的铰链接。

2.2 仿真试验装置的建模

仿真试验装置包括侧翻试验平台和半悬挂式农业机组两部分, 运用ADAMS对仿真试验装置进行多刚体动力学建模。建模过程如下:建立侧翻试验平台并在其与大地之间添加转动副, 且转动副带有驱动; 在拖拉机与半悬挂式机具之间建立球面副, 在侧翻试验台与半悬挂式机组的车轮之间建立接触。在侧翻试验过程中, 为防止机组相对试验平台发生侧滑, 在试验平台靠近旋转轴一侧固结有挡块, 并在挡块与机组的车轮轮胎外缘之间建立接触并设置接触力为0, 同时设置轮胎与试验平台间的摩擦因数使其足够大。根据半悬挂式农业机组的相关参数(以表1参数为例), 通过ADAMS/View模块, 对模型进行参数设置。

表1 机组基本参数 Table 1 Basic parameters of overall unit

在ADAMS/View中建立的仿真实验模型如图2所示。完成虚拟样机的建立之后, 对虚拟样机进行整体的约束关系、自由度数目的校验。

	Figure Option View Download New Window
	图2 ADAMS/View仿真模型Fig.2 Simulation model of ADAMS/View

2.3 静态侧翻仿真试验

半悬挂式农业机组的静态侧翻仿真试验按照《轮式拖拉机静侧翻稳定性试验方法》(NY/T1929— 2010)和《汽车静侧翻稳定性台架试验方法》(GB/T14172— 2009)中的有关规定进行, 保证仿真试验台的旋转速度不得大于10 ° /min。本仿真试验的试验参数设置如下:试验台的旋转角速度为0.1 ° /s; 仿真时间为450 s; 仿真步数为450步。

3 仿真结果分析

3.1 侧翻评定指标的分析

半悬挂式农业机组的轮胎与试验台间的接触力变化曲线如图3所示。图3中横坐标为仿真进行的时间t, 纵坐标为机组各轮胎随试验台旋转其垂向载荷t的变化情况。图3中CONTACT_L1.FY表示拖拉机左前轮胎与试验台间的接触力; CONTACT_L2.FY表示拖拉机左后轮胎与试验台间的接触力; CONTACT_L3.FY表示半悬挂式机具左侧轮胎与试验台间的接触力; CONTACT_R1.FY表示拖拉机右前轮胎与试验台间的接触力; CONTACT_R2.FY表示拖拉机右后轮胎与试验台间的接触力; CONTACT_R3.FY表示半悬挂式机具右侧轮胎与试验台间的接触力。

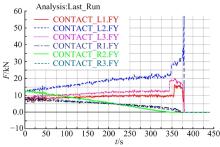	Figure Option View Download New Window
	图3 整机轮胎与试验台间的接触力变化曲线图Fig.3 Change curve of contact force between tire of overall unit and test bench

从仿真过程中整机轮胎与试验台间的接触力变化曲线可以看出:随着横向坡度角的增大, 机组左侧轮胎与侧翻试验平台的接触力慢慢增大, 机组右侧轮胎与侧翻试验平台的接触力慢慢减小。当机组右侧轮胎与侧翻试验平台的接触力减小到0时, 代表此刻该轮胎即将开始脱离试验平台。在整个仿真试验过程中, 机组右侧轮胎开始脱离试验平台的顺序为:拖拉机后轮右侧轮胎最先脱离侧翻试验平台, 拖拉机前轮右侧轮胎和半悬挂式机具的右侧轮胎几乎同时脱离试验台。

3.2 侧翻模型的验证

3.2.1 通过对比轮胎垂向载荷验证模型的正确性

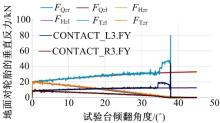对图3所示的接触力变化趋势进行分析, 并结合前文数学模型做出的相关假设, 对准静态侧翻仿真试验结果进行相应处理:规定CONTACT_L1.FY与CONTACT_L2.FY两者之和即 $F_{Tzl}$ 为地面作用于拖拉机内侧轮胎上的垂向反作用力, 规定CONTACT_R1.FY与CONTACT_R2.FY两者之和即 $F_{T z r}$ 为地面作用于拖拉机外侧轮胎上的垂向反作用力, 定义CONTACT_L3.FY为半悬挂式机具内侧轮胎上的地面垂向反作用力, 定义CONTACT_R3.FY为半悬挂式机具外侧轮胎上的地面垂向反作用力。将表1中各参数代入式(8)(9)(22)(23), 通过计算软件处理, 分别得到 $F_{Q z l} 、 F_{Q z r} 、 F_{H z l} 、 F_{H z r}$ 的变化曲线。将通过运用数学模型和ADAMS动力学模型两种方法求得的地面对机组各轮胎的垂向反作用力曲线进行对比, 并通过计算两种曲线的相关度来互相印证两种模型的正确性。图4为两种模型下机组各轮胎的地面垂向反作用力对比情况。鉴于本研究意在表征半悬挂式农业机组的横向静侧翻稳定性, 对机组的侧翻过程不作具体描述, 故在研究过程中, 重点对机组倾翻角度小于35° 的准静态侧翻过程进行分析。

	Figure Option View Download New Window
	图4 半悬挂式农业机组内外侧轮胎的地面垂向反力对比图Fig.4 Comparison of vertical ground reaction force between inner and outer sides of agricultural semi-mounted unit

由图4可知:在准静态侧翻阶段, 即机组的翻转角度小于35° 时, 运用数学模型计算得到的机组各轮胎的地面垂向反力曲线和运用动力学仿真计算得到机组各轮胎的地面垂向反力曲线具有非常高的重合度。利用图中倾翻角度小于35° 的实验数据, 处理得到数学模型计算结果和动力学仿真计算结果的相关系数, 计算得到 $F_{Q z l}$ 与 $F_{T z l}$ 的相关系数为0.93; $F_{Q z r}$ 与 $F_{T z r}$ 的相关系数为0.98; $F_{H z l}$ 与CONTACT_L3.Fy的相关系数为0.86; $F_{H z r}$ 与CONTACT_R3.Fy的相关系数为0.98。通过以上数据可以直观地看出, 两者具有很高的相关性。因此可以认为两者的计算结果是一致的, 从而初步互相印证了数学模型和动力学仿真模型的正确性。

3.2.2 通过对比横向载荷转移率验证模型的正确性

以准静态侧翻过程中的横向载荷转移率(LTR)作为评价指标, 通过比对两种模型求解得到的LTR并计算其相关度, 进一步对模型的正确性进行验证。利用Excel软件分别求出数学模型的LTR和动力学侧翻模型表征的LTR, 如图5所示。定义STLJ-LTR为运用数学模型方法计算获得的拖拉机的横向载荷转移率; 定义SSHJ-LTR为运用数学模型方法计算获得的半悬挂式机具的横向载荷转移率; 定义TLJ-LTR为运用动力学仿真方法获得的拖拉机的横向载荷转移率; 定义SHJ-LTR为运用动力学仿真方法获得的半悬挂式机具的横向载荷转移率。

	Figure Option View Download New Window
	图5 横向载荷转移率(LTR)对比图Fig.5 Comparison of LTR

如图5所示, 倾翻角度为0° ~35° 时, 由数学模型得到的地面对机组各轮胎的垂向反作用力曲线与经过动力学模型计算得到的反作用力曲线具有良好的重合度, 载荷横向转移率(LTR)随着倾翻角度的增大而不断增大。当倾翻角度大于35° 时, 由于试验平台靠近旋转轴一侧固结挡块的作用, 其对机组轮胎外缘作用力的大小和复杂程度随着倾翻角度的增加而迅速加剧。从而导致图中后期动力学模型曲线的剧烈跳动, 使得数学模型曲线与动力学仿真曲线出现了较大偏差。

经过计算, 拖拉机横向载荷转移率的数学模型曲线(STLJ-LTR)与动力学仿真曲线(TLJ-LTR)的相关系数为0.996; 半悬挂式机具横向载荷转移率的数学模型曲线(SSHJ-LTR)与动力学仿真曲线(SHJ-LTR)的相关系数为0.998, 两者均非常接近于1, 两种模型曲线的高度一致性证明了前文所建立的数学模型与动力学仿真模型的正确性。同时, 由图5所示的LTR与倾翻角度之间的关系可知:通过LTR来衡量机组的侧翻稳定性是可行的。

3.3 影响因素敏感度分析

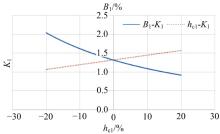
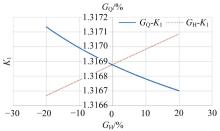
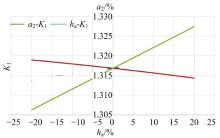
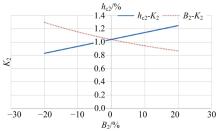
当进行半悬挂式农业机组的实际设计研发时, 若通过分析发现机组具有较差的侧翻稳定性, 则需要对机组整体的原始设计参数进行相应调整, 使其达到整机的设计及使用标准。对于拖拉机的侧翻稳定性, 选取其侧翻稳定性系数 $K_{1}$ 作为半悬挂式机组各参数对拖拉机侧翻稳定性影响大小的评价指标, 同时选取拖拉机的重心高度 $h_{c 1} 、$ 拖拉机的后轮轮距 $B_{1}$ 和拖拉机的质量 $G_{Q}$ 以及半悬挂式机具重心到牵引点的距离 $a_{2} 、$ 牵引点高度 $h_{a}$ 和半悬挂式机具的质量 $G_{H}$ 作为影响其侧翻稳定性系数 $K_{1}$ 的因素; 对于半悬挂式机具的侧翻稳定性, 选取侧翻稳定性系数 $K_{2}$ 作为半悬挂式机具的各设计参数对半悬挂式机具侧翻稳定性影响大小的评价指标, 同时选取半悬挂式机具的重心高度 $h_{c 2}$ 与半悬挂式机具的轮距 $B_{2}$ 作为影响半悬挂式机具侧翻稳定性系数 $K_{2}$ 的因素。规定将上述参数分别在设计值的20%范围内进行变化, 同时在保证单一变量的前提下(当一个参数变化时, 其他参数保持不变), 可得到 $h_{c 1} ⁃ K_{1} 、 B_{1} ⁃ K_{1} 、 G_{Q} ⁃ K_{1} 、 G_{H} ⁃ K_{1} 、 a_{2} ⁃ K_{1} 、 h_{a} ⁃ K_{1} 、 h_{c 2} ⁃ K_{2}$ 以及 $B_{2} ⁃ K_{2}$ 的敏感度曲线, 分别如图6~图9所示。

	Figure Option View Download New Window
	图6 B₁-K₁、h_c₁-K₁敏感度曲线Fig.6 Sensitivity curve of B₁-K₁、h_c₁-K₁

	Figure Option View Download New Window
	图7 G_Q-K₁、G_H-K₁敏感度曲线Fig.7 Sensitivity curve of G_Q-K₁、G_H-K₁

	Figure Option View Download New Window
	图8 a₂-K₁、h_a-K₁敏感度曲线Fig.8 Sensitivity curve of a₂-K₁、h_a-K₁

	Figure Option View Download New Window
	图9 h_c2-K₂、B₂-K₂敏感度曲线Fig.9 Sensitivity curve of h_c2-K₂、B₂-K₂

由图6可知:拖拉机的侧翻稳定性系数 $K_{1}$ 随着拖拉机重心高度 $h_{c 1}$ 的增大而增大, 随着后轮轮距 $B_{1}$ 的增大而减小, 且影响显著。

由图7可知:拖拉机的重量 $G_{Q}$ 和半悬挂式机具的重量 $G_{H}$ 对拖拉机的侧翻稳定性系数 $K_{1}$ 影响不显著。

由图8可知:拖拉机的侧翻稳定性系数 $K_{1}$ 随着牵引点高度 $h_{a}$ 的增大而增大, 随着半悬挂式机具重心到牵引点的距离 $a_{2}$ 的增大而减小。其中, 牵引点高度 $h_{a}$ 对侧翻稳定性系数 $K_{1}$ 的影响最大, 而重心到牵引点的距离 $a_{2}$ 对侧翻稳定性系数 $K_{1}$ 的影响不显著。

由图9可知:半悬挂式机具的侧翻稳定性系数 $K_{2}$ 随着其质心高度 $h_{c 2}$ 的增大而增大, 随着其轮距 $B_{2}$ 的增大而减小, 且质心高度对半悬挂式机具的侧翻稳定性系数 $K_{2}$ 的影响比轮距对其影响更为显著。

4 结论

(1)拖拉机的侧翻数学模型为: $LTR = \frac{2 [h_{a} b G_{H} + h_{c 1} G_{Q} (a + b)]}{B_{1} [(a + b) G_{Q} + b G_{H}]} \tan β,$ 半悬挂式机具的侧翻数学模型为: $LTR = \frac{2 h_{c 2}}{B_{2}} \tan β 。$ 通过数学模型和动力学模型计算结果的互相比较验证了两种模型的正确性, 并且证明了用LTR衡量机组侧翻稳定性的可行性。

(2)拖拉机和半悬挂式机具的重心高度和轮距均为影响其侧翻稳定性的重要因素, 重心高度越小, 轮距越宽, LTR就越小, 机具越稳定; 若要减小半悬挂式机具的LTR并且能够保证其他性能, 可采用降低牵引点高度 $h_{a}$ 及增大重心到牵引点距离 $a_{2}$ 的方法。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	季红波, 孔华祥, 房健. 农业机械静侧翻稳定性台架研发初探[J]. 中国农机化, 2011, 32(3): 90-92, 114. Ji Hong-bo, Kong Hua-xiang, Fang Jian. Research and development of statically lateral roll stability bench for agricultural machinery[J]. Chinese Agricultural Mechanization, 2011, 32(3): 90-92, 114. [本文引用:1]
[2]	曲俊娜. 铰接式工程车辆动态侧翻稳定性研究[D]. 长春: 吉林大学机械科学与工程学院, 2013. Qu Jun-na. Research on the dynamic rollover stability of articulated engineering vehicle[D]. Changchun: College of Mechanical Science and Engineering, Jilin University, 2013. [本文引用:1]
[3]	Reynolds S J, Groves W. Effectiveness of roll-over protective structures in reducing farm tractor fatalities[J]. American Journal of Preventive Medicine, 2000, 18(4): 63-69. [本文引用:1]
[4]	Thelin A. Rollover fatalities: Nordic perspectives[J]. Journal of Agriculture Safety and Health, 1998(4): 157-160. [本文引用:1]
[5]	李天成. 拖拉机侧翻试验的重要性及注意事项[J]. 四川农业与农机, 2013(5): 32-33. Li Tian-cheng. The importance and precautions of tractor rollover test[J]. Sichuan Agriculture and Agricultural Machinery, 2013(5): 32-33. [本文引用:1]
[6]	金智林, 张鸿生, 马翠贞. 基于动态稳定性的汽车侧翻预警[J]. 机械工程学报, 2012, 48(14): 128-133. Jin Zhi-lin, Zhang Hong-sheng, Ma Cui-zhen. Vehicle rollover warning based on dynamic stability[J]. Journal of Mechanical Engineering, 2012, 48(14): 128-133. [本文引用:1]
[7]	吴新烨, 葛晓宏, 罗树友, 等. 汽车侧翻稳定性研究[J]. 厦门大学学报: 自然科学版, 2010, 49(6): 815-818. Wu Xin-ye, Ge Xiao-hong, Luo Shu-you, et al. Study on stability of rollover of vehicle[J]. Journal of Xiamen University(Natural Science), 2010, 49(6): 815-818. [本文引用:1]
[8]	Eger Ralf, Kiencke Uwe. Modeling of rollover sequences[J]. Control Engineering Practice, 2003, 11(2): 209-216. [本文引用:1]
[9]	Gaspar P, Szaszi I, Bokor J. Reconfigurable control structure to prevent the rollover of heavy vehicles[J]. Control Engineering Practice, 2005, 13(6): 699-711. [本文引用:1]
[10]	姚宗伟. 铰接转向工程车辆侧倾稳定性研究[D]. 长春: 吉林大学机械科学与工程学院, 2013. Yao Zong-wei. Study on the rollover stability of articulated steer engineering vehicle[D]. Changchun: College of Mechanical Science and Engineering, Jilin University, 2013. [本文引用:1]
[11]	田晋跃, 贾会星. 铰接车辆侧倾过程动态仿真[J]. 农业机械学报, 2006, 37(7): 26-29. Tian Jin-yue, Jia Hui-xing. Dynamic simulation of the overturning of articulated vehicles[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(7): 26-29. [本文引用:1]
[12]	Prem H, Mai L, Brusza L. Tilt testing of two heavy vehicles and related performance issues[C]∥The 9th International Symposium on Heavy Vehicle Weights and Dimensions, Mechanical System Dynamics Pty Ltd, Pennsylvania, USA, 2006. [本文引用:1]
[13]	肖杰, 雷雨成, 张平, 等. 汽车静态最大侧倾稳定角及其影响因素敏感度分析[J]. 中国制造业信息化, 2006, 35(11): 64-67. Xiao Jie, Lei Yu-cheng, Zhang Ping, et al. Analysis of the maximum static stable roll angle of the vehicle and the sensitivity of the main influence factor[J]. Manufacture Information Engineering of China, 2006, 35(11): 64-67. [本文引用:1]
[14]	倪菲菲, 张良平. 汽车准静态侧翻的仿真分析[J]. 重庆理工大学学报: 自然科学, 2013, 27(3): 12-15. Ni Fei-fei, Zhang Liang-ping. Quasi static steering vehicle rollover simulation analysis[J]. Journal of Chongqing University of Technology(Natural Science) , 2013, 27(3): 12-15. [本文引用:1]
[15]	云善良, 张士新. 基于虚拟样机技术的玉米收获机拨禾轮运动仿真分析[J]. 农业装备与车辆工程, 2010(8): 13-15. Yun Shan-liang, Zhang Shi-xin. Simulation analysis for finger rotor of corn harvester based on virtual prototyping technology[J]. Gricultural Equipment and Vehicle Engineering, 2010(8): 13-15. [本文引用:1]
[16]	马丽娜, 杜岳峰, 宋正河, 等. 玉米收获机准静态横向稳定性数学建模与试验[J]. 农业机械学报, 2016, 47(7): 89-95. Ma Li-na, Du Yue-feng, Song Zheng-he, et al. Mathematical modeling and experiment of corn harvester quasi-static lateral stability[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7): 89-95. [本文引用:1]
[17]	金智林, 翁建生, 胡海岩. 汽车侧翻及稳定性分析[J]. 机械科学与技术, 2007, 26(3): 355-358. Jin Zhi-lin, Weng Jian-sheng, Hu Hai-yan. Analysis of vehicle’s rollover stability[J]. Mechanical Science and Technology, 2007, 26(3): 355-358. [本文引用:3]
[18]	麦莉, 宗长富, 高越, 等. 重型半挂车侧倾稳定性仿真与分析[J]. 吉林大学学报: 工学版, 2008, 38(增刊2): 5-10. Mai Li, Zong Chang-fu, Gao Yue, et al. Simulation and analysis of roll stability for heavy tractor semi-trailers[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(Sup. 2): 5-10. [本文引用:1]

2011

0.0

. 2011, 32(3):90-92,114

Research and development of statically lateral roll stability bench for agricultural machinery

农业机械静侧翻稳定性台架研发初探

Ji Hong-bo , Kong Hua-xiang , Fang Jian

季红波, 孔华祥, 房健

... 0 引言农业作业机组的侧翻稳定性是衡量机组安全性能优劣的重要指标之一^[1] ...

2013

0.0

. 2013, :-

Research on the dynamic rollover stability of articulated engineering vehicle

铰接式工程车辆动态侧翻稳定性研究

Qu Jun-na

曲俊娜

铰接式工程车辆比如集材机、装载机、铲运机等，具有机动性能好、转向半径小等优点广泛应用于能源开发、矿山开采、筑路等工程领域，工作环境比较恶劣，且装载质量比较大。同时由于铰接式工程车辆前后车体铰接在一起，自身结构不规则，使其在行驶转向时的横向稳定性较差，导致车辆在作业中极易发生侧翻危险事故。近年来铰接式工程车辆翻车事故屡屡发生，严重造成了生命和财产的损失。因此，铰接式工程车辆的稳定性和安全性问题已经成为国内外学者研究的热点。为了保护司机安全，国际标准ISO3471要求在工程车辆上安装翻车保护结构（ROPS），实现翻车时对司机的被动保护，但是不能从根本上抑制车辆倾翻。因此需要研究铰接式工程车辆的侧翻稳定性机理，采取主动安全技术抑制车辆倾翻。目前，国内研究机构和学者进行了大量的静态稳定性机理研究，但铰接式工程车辆的动态倾翻稳定性研究起步较晚还不完善。因此，本论文结合国家自然科学基金项目“非公路车辆防翻车主动安全技术研究”（No.51175216）、高等学校博士学科点专项科研基金（博导类）项目“工程车辆主动防倾翻系统设计理论与控制技术”（No.20100061110014）以及吉林大学研究生创新基金项目“非公路车辆翻车预警及主动防倾翻技术研究”(No.20121081)，在国内外研究成果的基础上，对铰接式工程车辆动态侧倾稳定性进行了分析。首先运用拉格朗日法建立了轮式装载机四自由度动力学模型；其次，自主搭建了车辆倾翻试验平台，设计了遥控装载机试验车，选取水平路面和斜坡路面转向工况对动力学模型进行了试验验证；最后，运用动力学模型对ZL50装载机动态侧翻稳定性进行了分析。本文围绕上述内容展开了如下工作： 1．对铰接式工程车辆倾翻稳定性的研究背景和意义进行了系统地论述，总结了铰接式工程车辆倾翻稳定性研究的国内外现状；阐述了铰接式工程车辆的转向过程，从一级稳定度和二级稳定度两方面分析了车辆在斜坡上行驶和转向时的静态横向稳定性；详细描述了几种车辆稳定性的评价指标，并对各自的优缺点进行了比较。 2．以轮式装载机为研究对象，对模型进行了基本假设，忽略了影响装载机横摆侧倾运动较小的因素，运用拉格朗日法建立了车辆四自由度动力学模型，并选用Matlab中ode15i解算指令对整车系统的运动微分方程进行了求解。所建立的模型简单易懂，实时性好，能够反映车辆侧向运动、横摆和侧倾的所有重要特性，为铰接式工程车辆侧倾稳定性机理的研究奠定了模型基础。 3．本文自主搭建了铰接式工程车辆倾翻车载试验平台，设计了能够完成直行、转向和爬坡运动的遥控装载机试验车，选取了水平道路和斜坡上转弯工况对轮式装载机横摆侧倾四自由度动力学模型进行了试验验证，动力学模型具有较高的精度。 4．选取横向载荷转移率作为评价车辆侧倾稳定性的危险指标，运用四自由度动力学模型对ZL50轮式装载机行驶转向特性进行了仿真，分析了车辆在不同速度、不同坡度以及不同时间内转向下的动态侧倾稳定性，并得出了某ZL50装载机稳定工作区域图，具有一定的实用价值，为进一步研究铰接式工程车辆侧翻预警技术和主动防倾翻控制系统奠定理论基础。铰接式工程车辆动态侧翻稳定性研究是主动防倾翻系统设计的理论基础，车辆倾翻机理的研究深入程度直接影响了主动防倾翻控制系统的精确性和有效性。因此，本文的工作可以为后续铰接式工程车辆主动安全技术的研究提供一定的依据。

... 由于半悬挂式挂接方式对于大型、重型及纵向尺寸较长的农业机械具有明显优势,使其在农业、林业中得到广泛的应用^[2],但因纵向尺寸长、悬挂点位置高、轮距较窄以及工况环境复杂等因素,其侧翻稳定性较差,翻车事故时有发生^[3,4] ...

2000

0.0

1998

0.0

2013

0.0

. 2013, (5):32-33 DOI:doi:10.3969/j.issn.2095-3615.2013.05.013

The importance and precautions of tractor rollover test

拖拉机侧翻试验的重要性及注意事项

Li Tian-cheng

李天成

正拖拉机侧翻试验主要是测试拖拉机在侧翻试验台上,倾斜拖拉机,拖拉机一侧车轮中任一车轮的支承平面法向反力至零以前或离开支撑面前的侧翻角。拖拉机的侧翻稳定角是通过比对左右侧的侧翻测试结果,以最小值为拖拉机的侧翻稳定角和最大侧翻稳定角。1拖拉机侧翻试验的重要性随着经济的发展,我国农业机械的应用范围越来越广,但其事故发生率也呈上升趋势。特别是拖拉机侧翻事故频频发生。造成侧翻事故的发生,分析原因主要

... 解决其固有的稳定性问题是半悬挂式农业机组发展的关键^[5] ...

2012

0.0

. 2012, 48(14):128-133 DOI:doi:10.3901/JME.2012.14.128

Vehicle rollover warning based on dynamic stability

基于动态稳定性的汽车侧翻预警

Jin Zhi-lin , Zhang Hong-sheng , Ma Cui-zhen

金智林, 张鸿生, 马翠贞

摘　要：为提高汽车侧翻预警算法的实时性及动态过程侧翻预警的精度,提出基于动态稳定性的汽车侧翻预警算法。考虑车轮侧倾外倾和侧倾转向及悬架变形外倾和变形转向对轮胎侧偏特性的影响,建立多自由度汽车侧翻动力学模型;应用汽车侧翻动力学理论及劳斯稳定性判据获得汽车侧翻动平衡稳定条件及汽车侧翻动平衡状态的抗干扰稳定条件,并提出侧翻动态稳定因子作为汽车动态稳定性的评价指标;融合汽车侧翻预警机理及侧翻动态稳定因子设计出基于动态稳定性的汽车侧翻预警算法;针对高速紧急工况下运动型多功能车侧翻过程进行动态侧翻预警仿真分析。结果表明,基于动态稳定性的汽车侧翻预警算法预警结果准确、实时,可提高动态过程汽车侧翻预警精度,降低侧翻危险的误报警率,有助于改善汽车防侧翻的主动安全性能。

... 目前,国内外关于车辆侧翻稳定性的研究大多集中在汽车^[6,7,8]、重型车辆^[9]和工程车辆^[10,11]等领域 ...

2010

0.0

. 2010, 49(6):815-818

Study on stability of rollover of vehicle

汽车侧翻稳定性研究

Wu Xin-ye , Ge Xiao-hong , Luo Shu-you

吴新烨, 葛晓宏, 罗树友

... 目前,国内外关于车辆侧翻稳定性的研究大多集中在汽车^[6,7,8]、重型车辆^[9]和工程车辆^[10,11]等领域 ...

2003

0.0

... 目前,国内外关于车辆侧翻稳定性的研究大多集中在汽车^[6,7,8]、重型车辆^[9]和工程车辆^[10,11]等领域 ...

2005

0.0

... 目前,国内外关于车辆侧翻稳定性的研究大多集中在汽车^[6,7,8]、重型车辆^[9]和工程车辆^[10,11]等领域 ...

2013

0.0

. 2013, :-

Study on the rollover stability of articulated steer engineering vehicle

铰接转向工程车辆侧倾稳定性研究[D]

Yao Zong-wei

姚宗伟

铰接转向工程车辆行驶路面复杂，工作环境恶劣，并且转弯时车辆重心会发生横向偏移，导致翻车事故发生几率较高。本文结合国家自然科学基金项目“非公路车辆防翻车主动安全技术研究”（NO.51175216）和高等学校博士学科点专项科研基金项目“工程车辆主动防倾翻系统设计理论与控制技术”（NO.20100061110014），对铰接转向工程车辆的侧倾稳定性进行系统研究，以轮式装载机为研究对象，提出了适用于铰接转向工程车辆的侧倾稳定性指标，并建立了7自由度非线性侧倾动力学模型，利用物理样机试验和虚拟样机仿真对所建立的动力学模型进行了验证，提出了改进铰接转向工程车辆的侧倾稳定性的措施。在综述国内外铰接转向工程车辆侧倾稳定性研究成果的基础上，结合铰接转向工程车辆的特性以及侧倾失稳原因，分析了铰接转向角、侧向加速度以及侧倾角等因素对现有指标的影响，讨论了现有各稳定性评价指标在铰接转向工程车辆上应用的不足，提出了适用于铰接转向工程车辆的侧倾稳定性指标。基于拉格朗日方程及虚功原理，建立了轮式装载机的7自由度非线性侧倾动力学模型，该模型全面考虑了车辆横摆、侧倾、俯仰等3个转动自由度以及纵向、横向、垂向3个平动自由度和后桥摆动自由度。模型以车辆的结构参数、铰接转向角、坡度角以及车速等作为输入，以车辆的动力学和运动学特性如侧倾角、侧倾角速度、侧向加速度、横向载荷转移率等作为输出。采用后向差分法对所建立的模型进行了数值求解。为验证所建立的动力学模型的可靠性，设计并制造了某型号铰接转向装载机的物理样机模型，进行了平面转弯，斜坡转弯以及越障等工况的试验；建立了铰接转向装载机虚拟样机模型，进行了对应工况下的虚拟样机仿真。通过对比侧倾动力学模型仿真结果、试验结果以及虚拟样机仿真结果，发现三者吻合程度较高，从而验证了所建立的动力学模型的正确性。利用7自由度非线性侧倾动力学模型，对某轮式装载机的侧倾稳定性进行了详尽的分析。所分析的参数中包括转弯速度、转弯半径、铰接转向角速度、坡度角、前桥到铰接轴线的距离、后桥到铰接轴线的距离、轮距以及摆动桥等。结果显示，摆动桥的存在对车辆在水平路面上的侧倾稳定性影响不大但对其在坡路上的侧倾稳定性影响非常大。分析结果对改进车辆的侧倾稳定性设计有一定的参考价值。根据铰接转向工程车辆侧倾稳定性分析结果，提出了基于摆动桥的改进方案。该方案中在现有的被动式摆动桥基础上增加检测组件、控制组件以及液压组件，使其成为主动式摆动桥；当车辆在水平路面上行驶时，该主动式摆动桥所实现的功能与被动式摆动桥基本一致，不会影响到车辆的越障性能；当车辆在坡路行驶时，该主动式摆动桥将会限制后桥的摆动以增强其侧倾稳定性。对改进后的车辆进行了仿真分析，结果显示该方案可以提高铰接转向工程车辆的侧倾稳定性。本文建立了全面分析铰接转向工程车辆特性的侧倾动力学模型，提出了适用于铰接转向工程车辆的侧倾稳定性指标，并将被动式摆动桥改进为主动式摆动桥以提高车辆侧倾稳定性。论文的研究工作为铰接转向工程车辆的安全性设计及主动防倾翻安全技术的开发提供了依据，对于提高铰接转向工程车辆作业的安全性和保护司机的生命安全具有重要意义。

... 目前,国内外关于车辆侧翻稳定性的研究大多集中在汽车^[6,7,8]、重型车辆^[9]和工程车辆^[10,11]等领域 ...

2006

0.0

. 2006, 37(7):26-29 DOI:doi:10.3969/j.issn.1000-1298.2006.07.007

Dynamic simulation of the overturning of articulated vehicles

铰接车辆侧倾过程动态仿真

Tian Jin-yue , Jia Hui-xing

田晋跃, 贾会星

建立了铰接车辆侧倾过程的数学模型,根据铰接车辆在侧倾过程中的一些重要特性,研究和分析铰接车辆侧倾的影响参数,通过Matlab和Veh-sim进行计算机仿真,得到铰接车辆在行驶速度30 km/h时突然转向,发生侧翻的危险时间出现在转向指令的1 s后,可能产生翻车的时间为4.5 s,若同时实施车辆制动,出现最大纵向和横向加速度.通过加大铰接车辆的轮距,降低车辆的重心高度,增加轮胎和路面的摩擦因数可以提高车辆的防侧倾性能.

... 目前,国内外关于车辆侧翻稳定性的研究大多集中在汽车^[6,7,8]、重型车辆^[9]和工程车辆^[10,11]等领域 ...

2006

0.0

... 将数学建模分析和动力学仿真应用于车辆静侧翻研究是一种行之有效的方法,国内外许多学者基于此方法取得了理想的研究成果,Prem等^[12]基于虚拟样机技术进行了车辆的静态侧翻稳定性仿真试验,并研究了载荷分配对车辆侧翻稳定性的影响 ...

2006

0.0

. 2006, 35(11):64-67 DOI:doi:10.3969/j.issn.1672-1616.2006.11.018

Analysis of the maximum static stable roll angle of the vehicle and the sensitivity of the main influence factor

汽车静态最大侧倾稳定角及其影响因素敏感度分析

Xiao Jie , Lei Yu-cheng , Zhang Ping

肖杰, 雷雨成, 张平

为更加准确地求解汽车静态最大侧倾稳定角,建立了综合考虑悬架组合角刚度和轮胎垂直刚度的汽车静态侧翻模型.应用该模型,对某型号客车的静态最大侧倾稳定角进行了计算,将求解结果和其他侧翻模型以及试验数据对比,结果表明该模型计算结果和试验数据很接近.利用该模型,还进行了侧倾稳定角主要影响因素的敏感度分析.

... 肖杰等^[13]建立了汽车的静态侧翻模型,计算得到最大侧翻稳定角,并且对汽车静态侧翻稳定性的影响因素进行了敏感度分析 ...

2013

0.0

. 2013, 27(3):12-15

Quasi static steering vehicle rollover simulation analysis

汽车准静态侧翻的仿真分析

Ni Fei-fei , Zhang Liang-ping

倪菲菲, 张良平

... 倪菲菲等^[14]建立了车辆行驶过程中的准静态侧翻模型,推导了侧翻因子的计算公式,通过仿真方法较全面地分析了汽车侧翻的影响因素 ...

2010

0.0

. 2010, (8):13-15 DOI:doi:10.3969/j.issn.1673-3142.2010.08.004

Simulation analysis for finger rotor of corn harvester based on virtual prototyping technology

基于虚拟样机技术的玉米收获机拨禾轮运动仿真分析

Yun Shan-liang , Zhang Shi-xin

云善良, 张士新

运用虚拟样机技术,可简化机械产品的设计开发过程,缩短产品的开发周期和降低开发成本,获得最优化和创新的设计产品.阐述虚拟样机的先进性及应用软件ADAMS的功能特点,通过玉米收获机拨禾轮的仿真设计给出虚拟样机的具体应用.

... 可见,对于汽车稳定性的研究已经达到了很高的水平^[15,16],但是对于半悬挂式农业机组的安全稳定性有待进一步研究 ...

2016

0.0

. 2016, 47(7):89-95 DOI:doi:10.6041/j.issn.1000-1298.2016.07.013

Mathematical modeling and experiment of corn harvester quasi-static lateral stability

玉米收获机准静态横向稳定性数学建模与试验

Ma Li-na , Du Yue-feng , Song Zheng-he

马丽娜, 杜岳峰, 宋正河

On the basis of studying both at home and abroad, not only the orientation of the corn harvester rear axle pivot had been considered, but also the track width differences between front axle and rear axle had been taken into account, thus a more accurate quasi static lateral stability mathematical model was constructed. Then lateral stability experiment and simulation analysis were carried out in order to verify the validity of the model. Accordingly the lateral stability influence factors were obtained. Afterwards, each influence factor was firstly set at a certain range of values, then the value range of each influence factor was converted into an identical range \[-1,1\], taking advantage of encoding transform. Therefore the curve of lateral stability indicator λ changing with the varying of different influence factors could be drawn in the same picture which could directly show the impact extent each factor on the lateral stability. The analysis results showed that the main influence factors of corn harvester quasi static lateral stability were wheel base x, the height of corn harvester center of gravity h, the distance between the center of gravity and front axle a, as well as front axle track width t1. In the end, this paper also put forward several measures to improve the lateral stability of the whole machine. When the center of gravity is lowered by 100mm, the load ratio of the front and rear axle is increased to 4, as well as the symmetric machine model is adopted. The result shows that the alteral critical angle of the corn harvester can be increased from 24.8° to 29.52° and the lateral stability can be raised by 19.03%. The establishment of corn harvester quasi static lateral stability mathematical model can provide a foundation for corn harvester overall arrangement and structure design.

综合玉米收获机后桥摇摆轴结构以及前、后桥轮距不等因素，建立了玉米收获机准静态横向稳定性数学模型，并进行了仿真分析和整机侧倾试验，二者结果相对误差仅为2.59%，验证了该模型的正确性，明确了整机横向稳定性的影响因素。然后，利用编码变换，将各影响因素的变化范围转换到\[-1,1\]，实现了不同影响因素对横向稳定性系数λ影响程度的可比性，从而明确了玉米收获机准静态横向稳定性的关键影响因素是：轴距x、整机重心高度h、重心到前桥的距离a以及前轮轮距t1。最后，提出了提高整机横向稳定性的措施。研究结果表明，整机重心h降低100mm，空载前后桥载荷比i提高至4，且采用对称布置的试验样机，横向稳定性可提高19.03%。

... 可见,对于汽车稳定性的研究已经达到了很高的水平^[15,16],但是对于半悬挂式农业机组的安全稳定性有待进一步研究 ...

2007

0.0

. 2007, 26(3):355-358 DOI:doi:10.3321/j.issn:1003-8728.2007.03.021

Analysis of vehicle#cod#x02019;s rollover stability

汽车侧翻及稳定性分析

Jin Zhi-lin , Weng Jian-sheng , Hu Hai-yan

金智林, 翁建生, 胡海岩

通过对三自由度线性汽车侧翻模型的理论分析,得到了汽车侧翻系统准动态稳定因子.与静态稳定因子进行了比较,并应用劳斯-赫尔维茨稳定性判据得到了汽车侧翻系统的稳定性条件.通过数值仿真分析得到了汽车结构参数对侧翻稳定区域的影响,并通过固定转角及变车道行驶两个实例仿真来验证,得到结果与理论分析一致.

... 针对现有半悬挂式农业机组静侧翻稳定性研究的不足,本文充分研究了国内外车辆静态侧翻稳定性的相关理论^[17,18],结合半悬挂式农业作业机组的特殊性,建立了半悬挂式农业机组的侧翻数学模型和ADAMS动力学模型,着重分析了机组静侧翻稳定性的影响因素及其敏感度,进而给出一种表征半悬挂式农业机组静侧翻稳定性的新方法,为半悬挂式农业机组的优化设计提供了理论参考 ...

... 并且根据横向载荷转移率的定义^[17],令: FQzl1+FQzl2=FQzl,FQzr1+FQzr2=FQzr ...

... 定义LTR为左、右轮胎垂向载荷之差与总载荷的比值^[17]: ...

2008

0.0

. 2008, 38(增刊2):5-10

Simulation and analysis of roll stability for heavy tractor semi-trailers

重型半挂车侧倾稳定性仿真与分析

Mai Li , Zong Chang-fu , Gao Yue

麦莉, 宗长富, 高越

摘　要：针对重型半挂车侧倾稳定性问题,建立了车速可变的八自由度动力学模型。在变车速情况下进行了阶跃转向输入下的仿真,并分析了重型半挂车结构参数和车速对其侧翻稳定性的影响。仿真结果表明:牵引车驱动轴为侧倾稳定性危险车轴,当车速过高或前轮转角过大时,首先离地;增大各轴轮距、降低簧载质量质心高度、提高半挂车悬架侧倾刚度、降低牵引车悬架侧倾刚度能够有效地提高重型半挂车侧倾稳定性。