作者简介:董惠娟(1968-),女,教授,博士生导师.研究方向:功率超声技术.E-mail:dhj@hit.edu.cn
针对驻波悬浮辐射/反射面之间(谐振腔内)的非轴对称声场,首先通过COMSOL仿真得到第3悬浮模式下声场典型截面上的声压分布。然后,采用Matlab编程将此声压进行Radon变换,得到该截面上各方向的激光测振仪(LDV)速度输出,并将其与实验得到的LDV速度输出进行对比,验证了LDV速度输出与声场声压的对应关系。最后,基于FBP算法并通过Matlab编程将实验中获得的LDV速度输出进行重建,得到该截面的声压分布,对比COMSOL仿真结果,从而验证非轴对称驻波声场的识别效果。
Measuring the acoustic pressure of standing wave is the basis of acoustic levitation. The non-axisymmetric acoustic field within the resonance cavity is analyzed. Firstly, the acoustic pressure distribution on the typical cross-section of the acoustic field in the third levitation mode is obtained by COMSOL simulation. The simulated acoustic pressure is Radon transformed to obtain the simulated LDV velocity output, which is compared with the experiment results to verify the relationship between LDV velocity output and acoustic pressure distribution. Then, based on Filer Back Projection (FBP) algorithm, a self-written MATLAB code is used to reconstruct the LDV velocity output in the experiment and obtain the acoustic pressure distribution of the cross-section, which is compared with the COMSOL simulation results. The identification effect of the non-axisymmetric standing wave acoustic filed is verified.
与其他悬浮技术相比, 超声驻波悬浮的显著优势是生物相容性好、横向稳定性良好[1], 且对被悬浮物性质没有要求[2], 因此被广泛应用于材料及药物制备[3, 4, 5, 6]、生物研究[7, 8, 9, 10]、液滴动力学研究[11, 12]、微小物体的传输与操作[13, 14, 15, 16, 17, 18]等领域。
声波在谐振腔内反复叠加, 对于辐/反射面均为平面的谐振腔, 当谐振腔长度为声波半波长的整数倍时, 谐振腔内将形成驻波声场。然而, 对于辐/反射面均为凹球面的情况, 平面波假设便不再适用[19], 辐/反射面尺寸和相对位置不同, 所形成的声场形状与声压大小都将改变。而且, 当谐振腔内存在悬浮物时, 由Gor'kov理论[20]可知, 物体将悬浮于声压势阱(声压为零)偏下的位置, 悬浮物的存在及其振动会改变声压分布, 因此, 声场声压分布的非接触在线测量不仅可以确定声压势阱所在的位置, 还可以在线监视声压的稳定状况, 成为制约超声驻波悬浮研究的瓶颈技术[21]。
目前, 空气中通常采用麦克风测量声压分布, 然而麦克风本身会干扰声场[22]。激光测振仪(LDV)测量设备具有非接触、无干扰、分辨率高、频响高、频带宽等[23]优势, 可以为声场非接触在线测量提供技术支持[15, 21]。近几年, LDV在测量水声方面取得了很大进展, 人们利用LDV测量水声声压[23], 获得声在水中传播时水媒质质点的振速, 甚至得到声波在水中及透明固体中随时间传播的规律[24]。然而, 利用LDV测量空气中声压分布的研究进展比较缓慢。最先将LDV引入空气中声压测量的是日本学者Nakamura等[25], 但当时他们仅针对均匀声压分布情况, 即LDV激光测量路径上声压幅值为常数, 给出了测量原理及方法。此后日本学者Koyama[16]以及巴西学者Andrade等[2, 26, 27]也利用LDV测量声场, Andrade仅指出LDV速度输出与声压沿激光路径积分成正比, 但他们并没有将LDV速度输出结果重建成声压。然而, 非轴对称声场非常普遍, 例如, 当单轴式超声悬浮器的辐/反射面的轴线不同轴时, 或者在超声悬浮传输时, 其声场都是非轴对称的。
本文针对超声驻波形成的非轴对称声场, 利用LDV实验测得的速度输出, 结合滤波反投影(Filtered back projection, FBP)原理[23], 重建了所研究截面上的声压分布。
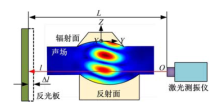
由于声场的存在, 导致其周围空气折射率发生改变[15, 25], 图1为利用LDV测量声场的示意图, 当激光穿过声场所在区域时, 其光程发生改变。在声场附近放置一个静止的反光板, 激光光程的改变将等效为反光板以
式中:n、c和ρ 分别为空气中的折射率、声速和空气密度; L为激光发射头与反光板之间的距离。
考虑到谐振腔内的声压呈正弦式(或余弦式)周期变化, 忽略高声场强度下的高次谐波的产生,
式中:p(l)为l处声压幅值, 基于式(1)(2), 当谐振腔内形成驻波时, LDV速度输出幅值
如式(3)所述,
为了得到声场中声压的分布, 需要将
对于非轴对称声场的重建, 可以采用滤波反投影(FBP)法。FBP法可以通过傅立叶切片定理在极坐标下推导出来[23], FBP重建方法的输入量为
 | 图2 在激光扫描方向θ 情况下平面B声压分布与其υ LDV的关系Fig.2 Relationship between acoustic pressure of plane B and its υ LDV when laser beam scans at θ direction with a spacing of τ |
利用FBP法重建声压分布可由下式实现:
其中
式中:
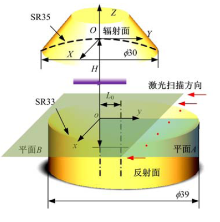
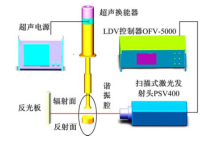
非轴对称声场在单轴式悬浮器谐振腔内部产生, 由朗之万型换能器产生频率为21 028 Hz的超声波, 谐振腔结构参数如图3所示, 实验中采用的凹球反射面的截面直径为39 mm; 球面半径为33 mm; 辐射面截面直径为30 mm; 球面半径为35 mm。谐振腔长度为H, 且辐/反射面轴线间距(下文简称轴偏距)为L0。换能器由自制的超声电源驱动, 实验时工作频率为21 028 Hz, 实验前用LDV标定换能器端面振速与其两端电压的关系。标定时将电压由0 V变化到35 V, 在这一区域, 非线性误差为0.9%。换能器端面小振幅振动, 实验过程中换能器不发热, 输出振幅恒定。本实验选定第3悬浮模式某截面进行LDV扫描测量, 实验系统示意图如图4所示。本实验将LDV设备固定, 而将反射面绕着
采用C#编程控制电动推杆(日本Harmonic公司)推动反射面运动, 可以实现谐振腔长度以3 μ m的增量变化。利用LDV(PSV400 激光扫描头, OFV-5000 控制器, 德国Polytec公司)可以在声场某一截面上进行扫描, 配套的软件可以直接进行快速傅立叶变换(FFT)。实验中由于激光头与声场距离远大于声场与反光板距离, 可以近似认为, LDV以平行光束测量声场, 如图3所示, 各扫描点(共J个扫描点)之间的距离通过反光板进行标定。
为了找到不同悬浮模式对应的谐振腔长度, 以便针对其中一个悬浮模式进行声场声压分布识别的研究, 通过COMSOL仿真与LDV实验两种方法, 分别获得各悬浮模式对应的谐振腔长度, 并将两者做对比。
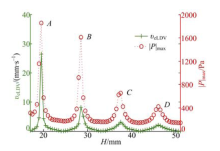
仿真时, 利用COMSOL软件中的参数化扫描功能, 设置谐振腔长度H以0.5 mm增量变化, 从17 mm增加到51 mm(与实验一致), 分别得到各谐振腔长度下对应的谐振腔内的声压分布, 谐振腔长度H与其对应的最大绝对声压|P|max关系如图5中虚线所示。实验时, 激光穿过(0, 0, -9) mm点, 该点声压基本等于谐振腔内最大绝对声压。同样将谐振腔长度由17 mm变化到51 mm, 记录每一谐振腔长度对应的
从图5可看出, 实验数据υ eLDV的峰值位置与仿真数据|P|max的峰值位置相同。各峰值点对应的谐振腔长度为19.5、28.5、37.5和46 mm, 分别对应第2~5悬浮模式。由于第1悬浮模式时最大声压发生在辐/反射面凹腔内, 该悬浮模式无法通过这一实验获得。考虑到实验观察方便, 且具有易于区分的声压结构等因素, 选择第3悬浮模式进行仿真与实验验证。
3.2.1 采用COMSOL获得声场声压
本文谐振腔内非轴对称声场来源于轴偏距L0, 设置非轴对称声场仿真基本参数如表1所示。这里辐射面振幅设为1 μ m, 对于其他振幅下的声压值, 乘以一个比例系数即可。为了防止谐振状态时出现强烈的非线性现象, 使谐振腔长度为28 mm, 此时谐振腔内声压较稳定。
| 表1 声场仿真基本参数 Table 1 Basic parameters of acoustic field simulation |
在COMSOL中按照图3谐振腔结构进行建模, 得到第3悬浮模式下谐振腔内YOZ截面处绝对声压分布如图6所示。
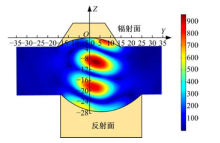 | 图6 第三悬浮模式下谐振腔内YOZ截面处绝对声压分布Fig.6 Absolute acoustic pressure distribution in YOZ section of resonance cavity in third levitation mode |
从图6可以看出, 由于辐/反射面轴偏距的存在, 使得声场声压关于Z轴非对称。理论上可以对整个声场进行扫描和声场重建, 然而需要大量时间, 因此, 实验选定截面Z=-20.5 mm, 即图3中平面B, 作为研究对象, 仿真时, 选取截面上出现最大绝对声压的相位(0° 相位或180° 相位, 该相位指辐射面振动相位), 认为声压在该相位时,
3.2.2 采用Radon变换获得υ sLDV
为了验证
实验中谐振腔结构如图3所示, L0=6 mm, H=28.0 mm。与仿真中相对应, 选择Z=-20.5 mm处的横截面(平面B)进行扫描。本实验中LDV在平面B上以1° 为增量从0° 扫描到89° , 然后将实验数据对称处理, 得到0° 到179° 共180个方向的
从图8中可以看出, 当θ =90° 时, X=0 mm附近
3.3.1 声场的仿真重建
基于FBP算法并利用Matlab编程, 将平面B(z=-20.5 mm截面) 上各方向的
为了进一步定量观察FBP重建效果, 且考虑到声压分布关于x=0对称, 分别得到不同x位置归一化声压与y的关系曲线, 如图9(a)所示。从曲线上可以看出:仿真声压与重建声压吻合较好。其误差如图9(b)所示, 可以看出:当x=0, 仿真声压与重建声压之间相对误差在± 0.02, 因为该处声压较强, 声场大部分能量集中在这个地方, 随着x的增大, 二者相对误差扩大, 最大达到0.2(x=30 mm), 但是二者的曲线在形状上仍然是吻合的, 也就是说, 利用FBP法可以识别声场声压分布的整体形状。
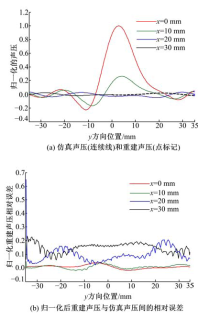 | 图9 不同x位置对应的归一化声压及相对误差Fig.9 Normalized acoustic pressure and relative error correspond to different x location |
3.3.2 声场的实验重建
利用FBP算法对
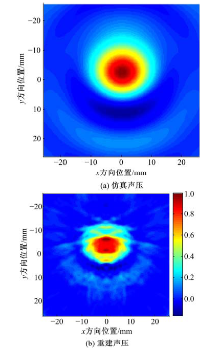 | 图10 平面B(52 mm× 52 mm)处COMSOL仿真声压与FBP重建声压对比Fig.10 Comparison between simulated acoustic pressure and reconstructed acoustic pressure of plane B(52 mm× 52 mm) |
从图10可以看出, 采用
本文利用激光测振仪实现了空气中非轴对称声场的识别, 即用实验测得的LDV速度输出进行声场声压分布的重建。其中, 非轴对称声场由单轴式悬浮器产生, 换能器工作频率为21 028 Hz, 辐射/反射面距离为28.0 mm, 辐射/反射面轴偏距为6 mm, 仿真和实验测试平面距离辐射面为20.5 mm。通过仿真和实验, 证实了Radon变换可以利用声场声压仿真获得LDV速度输出, 验证声场任意截面上LDV速度输出与声压分布的关系; 而FBP算法则可以将LDV实验测得数据重建为声压分布。值得注意的是, 在利用LDV实现声场测量过程中, Radon变换与FBP算法为互逆过程。本文提供的声场识别方法可以利用LDV间接非接触获得所研究声场的声压分布, 为识别声场静态声压分布提供了一种新方法。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|