引用本文
王旭, 欧阳继红, 陈桂芬. 基于垂直维序列动态时间规整方法的图相似度度量[J].吉林大学学报（工学版）, 2018,48(4): 1199-1205
WANG Xu, OUYANG Ji-hong, CHEN Gui-fen. Measurement of graph similarity based on vertical dimension sequence dynamic time warping method[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 1199-1205  
Doi:10.13229/j.cnki.jdxbgxb20170600
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有 吉林大学学报编辑部
基于垂直维序列动态时间规整方法的图相似度度量
王旭1,2, 欧阳继红1,2, 陈桂芬3
1.吉林大学 计算机科学与技术学院,长春130012
2.吉林大学 符号计算与知识工程教育部重点实验室,长春130012
3.吉林农业大学 信息技术学院,长春 130118
通讯作者:欧阳继红(1964-),女,教授,博士生导师.研究方向:数据挖掘,时空推理.E-mail:ouyj@jlu.edu.cn

作者简介:王旭(1982-),男,博士研究生.研究方向:数据挖掘,图挖掘.E-mail:xuwang10@mails.jlu.edu.cn

基金:国家自然科学基金项目(61472157,61602204,61402195).
摘要

针对图相似度度量过程中复杂度高、信息缺失的问题,采用将图转换为广义树,将广义树表示为垂直维序列的方法,通过计算垂直维序列的距离度量图的相似度。该方法把度量图相似度的问题简化为计算垂直维序列距离的问题。垂直维序列不仅包含了顶点标号、入度和出度信息,而且体现了顶点的层次结构特性,保留了图中的路径信息。与现有方法相比,该方法在度量过程中考虑了更多的图信息,并将时间复杂度降至 O( n2)。

关键词: 人工智能; 图相似度度量; 动态时间规整; 垂直维序列; 距离计算; 时间复杂度
中图分类号:TP18 文献标志码:A 文章编号:1671-5497(2018)04-1199-07
Measurement of graph similarity based on vertical dimension sequence dynamic time warping method
WANG Xu1,2, OUYANG Ji-hong1,2, CHEN Gui-fen3
1.College of Computer Science and Technology, Jilin University, Changchun 130012, China
2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun 130012, China
3.College of Information Technology, Jilin Agricultural University, Changchun 130118, China
Abstract

To solve the problems of high complexity and information loss in the process of measuring graph similarity, a method to calculate the distance of vertical dimensional sequences is proposed, which is used to measure graph similarity. Using this method, the graph is converted into the generalized tree, which is regarded as the vertical dimensional sequences. This method simplifies the graph similarity measurement to the distance calculation of the sequences. The vertical dimensional sequences not only obtain labels, in-degrees and out-degrees information of vertices, reflect level structural property of vertices, but also reserve the path information of graph. Compared with the existing graph similarity methods, this method involves more graph information in the process of graph similarity measurement, and decreases the time complexity to O( n2).

Keyword: artificial intelligence; graph similarity measure; dynamic time warping; vertical dimensional sequences; distance calculating; time complexity
0 引 言

数据挖掘、计算机视觉、社会网络、生物信息学、智能农业等领域中产生了大量的图数据[1, 2], 通过应用图相似度度量方法能够有效解决图数据的分类问题。所以, 如何快速和准确地度量图的相似度一直是研究图数据分类的重要问题[3, 4]。现有方法通过计算图的公共路径度量图的相似度, 其时间复杂度高, 如随机路径图核的时间复杂度为O(n3)[5, 6]; 最短路径图核的时间复杂度为O(n4)[7]; 图公共路径核函数的时间复杂度为O(n3)[8]等。一些度量图相似度的方法是将图直接转换为序列[9, 10], 主要思想是基于W-L图核方法[11, 12], 虽转换过程简单, 但复杂度仍为O(n3)。W-L图核方法通过度量序列的相似度实现对图相似度的度量, 而度量序列相似度的方法还包括动态时间规整算法(Dynamic time warping, DTW)[13, 14]、最长公共子序列方法[15]和所有公共子序列方法[16, 17], 但这些方法均不能直接用于度量图的相似度。一般地, 度量图的信息越多, 相似度准确性越高, 而上述方法仅仅考虑了图的顶点标号(Label)信息, 忽略了顶点重要的入度(In-degree)和出度(Out-degree)信息, 增加对顶点入度和出度信息的度量, 能够提高图相似度的准确性。但同时, 度量信息越多, 计算量越大, 导致度量效率越低[18, 19]。因此, 如何度量图中更多的信息, 并降低时间复杂度, 成为提高度量图相似度准确性和效率的关键。

本文提出了基于垂直维序列的动态时间规整方法的图相似度度量, 垂直维序列自左向右层次地、自上而下垂直地体现了图的结构特性。为了得到更加准确的度量结果, 在计算垂直维序列距离时, 该方法使用三元组(l, i, o)代替顶点标号l, 充分度量了顶点的入度和出度, 解决了图中边信息缺失的问题, 且时间复杂度低。

1 图转换为广义树方法

本文研究的图是顶点带标号的有向图, 将图转换为具有层次结构的广义树, 广义树的定义如下:

定义1 图G = (V, E), V和E分别表示G的顶点集和边集。取G中入度为0的顶点作为树T = (N, E1)的根, N和E1分别表示T的结点集和边集。记T的根结点的层Level (Root) = 1, T中子结点的层为其父结点的层加1, 当任一结点v为多个结点的子结点, 则v的层为其父结点的层的最小值, 并记Level (v) = min{Level(Father(v))} + 1。若G中所有顶点均已标记出层, 且N = V, E = E1, 则称T为G的广义树。

图G中顶点的标号l、入度i和出度o表示为广义树结点的三元组(l, i, o)。从根结点自上而下指向叶子结点的路径的结点序列称为垂直维序列, 垂直维序列的结点分布于不同的层上, 即在垂直维序列中, 同一层上只能有一个结点。图转换为广义树算法的思想如下:

算法1 图转换为广义树算法

输入:有向图G

输出:广义树T的垂直维序列t

步骤1 取G中的任一顶点为T的根结点Root(T) = Vertex(G), N = {Root}, 根结点指向的下一顶点为根结点的子结点Children(Root)。

步骤2 E表示图G中边的集合, |E|表示图G的边数, E1初始为空集; G中任一顶点v的层初始为0, Level (v) = 0, 根结点的层为1, 记Level (Root) = 1; G中顶点由三元组(l, i, o)表示。

步骤3 若|E| = 0, 转到步骤4。

步骤4 若结点p没有子结点, 或p所有子结点的层不高于p的层, Level(Children(p)) ≤ Level(p), 则称p为叶子结点, p = Leaf。

步骤5 (p, q)表示顶点p到顶点q的边, 若(p, q)∈ E, 转到步骤6, 否则, 转到步骤7。

步骤6 若Level (q)≠ 0, Level (q)=min{Level (p) + 1, Level(q)}, 否则, Level (q)=Level(p)+1, N=N+q, e=(p, q), p = q, q=Children(q), 转到步骤3。

步骤7 p=Father(p), 从E中删除边(p, q), E=E-e, 并将e保存到集合E1中, E1=E1+e, 转到步骤3。

步骤8 广义树T = (N, E1), 垂直维序列t的结点分布于不同的层上, t=(Root(l, i, o)…Children(l, i, o)…Leaf(l, i, o)), Level(Root(l, i, o))≠ Level(Children(l, i, o)) ≠ Level (Children(l, i, o))。

步骤9 输出 t。

算法1将图G等价地转换为广义树T=(N, E1 ), 与G的顶点集V相比, N的结点由三元组(l, i, o)表示, 保留了图中顶点的入度和出度信息, 且分为不同的层; E1保存了删除的边, 执行完步骤3, E1包含了图中所有的边, 在E1中可找到根结点到叶子结点的路径, 用于表示垂直维序列t, t体现了图的自左向右的层次结构特性和自上而下的垂直结构特性, 保留了图的路径信息。

广义树的结点分为不同的层, 根结点的层为1, 其它结点的层初始为0, 兄弟结点在同一层上。广义树实质是顶点具有层次标记的图, 完全保留了原图的信息, 使从广义树中提取的垂直维序列更好地体现出原图的路径信息, 解决了在图转换为序列过程中信息缺失的问题, 确保度量垂直维序列的结果更准确地反映出原图的相似度。本文通过计算垂直维序列的距离度量图的相似度, 垂直维序列是广义树中根结点指向叶子结点的路径, 无向图的边没有反映出广义树结点间的指向关系, 不能提取出垂直维序列; 在实际的应用中, 也要求用有向边表示两个顶点之间的关系, 故本文没有考虑无向图。为保证度量的可靠性, 选择入度为0的顶点作为广义树的根结点, 若入度为0的顶点有多个, 则选择标号相同的顶点为根结点。

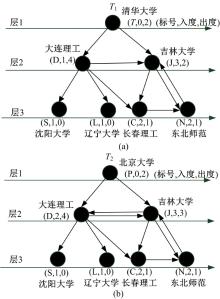
以国内一些高校的网站如清华大学(Tsinghua University)、北京大学(Peking University)、吉林大学(Jilin University)、东北师范大学(Northeast Normal University)、长春理工大学(Changchun University of Science and Technology)、大连理工大学(Dalian University of Technology)、辽宁大学(Liaoning University)、沈阳大学(Shenyang University)为例建图。每个网站作为图的顶点, 每个链接作为图的边, 得到下面两个图G1和G2, 如图1所示。在G1和G2中, 选取入度为0的顶点(清华大学和北京大学)为根结点, 得到广义树T1和T2, 如图2所示。

图1 有向图G1和G2Fig.1 The directed graphs G1 and G2

图2 G1和G2的广义树:T1和T2Fig.2 The generalized trees of G1and G2: T1and T2

在图2的T1中, 结点(J, 3, 2)为结点(T, 0, 2), (D, 1, 4)和(N, 2, 1)的子结点, (T, 0, 2), (D, 1, 4)和(N, 2, 1)的层分别为1, 2和3。根据算法1, 取结点(J, 3, 2)最小的层, 所以有:Level((J, 3, 2)) = min{Level((T, 0, 2)) + 1, Level((D, 1, 4)) + 1, Level((N, 2, 1)) + 1} = min{1+1, 2+1, 3+1}= 1 + 1 = 2。

广义树T1和T2表示为垂直维序列t1和t2, 使用三元组(l, i, o)表示t1和t2中的结点, 如表1所示, T1和T2垂直维序列分别为t1:{(T, 0, 2) (D, 1, 4) (S, 1, 0), (T, 0, 2) (D, 1, 4) (L, 1, 0), (T, 0, 2) (D, 1, 4) (C, 2, 1), (T, 0, 2) (J, 3, 2) (C, 2, 1), (T, 0, 2) (J, 3, 2) (N, 2, 1)}, t2:{(P, 0, 2) (D, 2, 4) (S, 1, 0), (P, 0, 2) (D, 2, 4) (L, 1, 0), (P, 0, 2) (D, 2, 4) (C, 2, 1), (P, 0, 2) (J, 3, 3) (C, 2, 1), (P, 0, 2) (J, 3, 3) (N, 2, 1)}。

表1 T1和T2的垂直维序列 Table 1 The vertical dimensional sequences of T1 and T2
2 垂直维序列的动态时间规整方法
2.1 三元组的度量

t1和t2为广义树T1和T2的垂直维序列, t1和t2的距离为t1和t2中结点三元组之间的距离。当两个三元组的标号、入度和出度均相同时, 它们之间的距离为0。若结点标号不同, 则两个三元组的距离为ε ; 若结点标号相同, 则距离可通过计算两个三元组结点间的入度差和出度差所获得。其中ε 为参考值, 可根据图的复杂程度, 为ε 设定一个合适的值。用d((l, i, o)1, (l, i, o)2)表示t1和t2中两个三元组的距离, 则有下式成立,

dl, i, o1, l, i, o2=0, ifl1=l2, i1=i2, ando1=o2(i1-i2)+(o1-o2), ifl1=l2ε, otherwise(1)

式中:l1, i1, o1分别表示t1中结点的标号、入度和出度; l2, i2, o2分别表示t2中结点的标号、入度和出度。

对于表1中的两个垂直维序列(t1)1和(t2)1, (t1)1 = ((T, 0, 2) (D, 1, 4) (S, 1, 0)); (t2)1= ((P, 0, 2) (D, 2, 4) (S, 1, 0))。(t1)1与(t2)1的距离由dtw(1, 1)表示, dtw(1, 1)可由d((l, i, o)k, (l, i, o)l)递归计算得出, k表示(t1)1中三元组的序号, l表示(t2)1中三元组的序号, 结合式(1)有下式成立:

dtw1, 1=0, ifk=0andl=0∞, ifk=0andl≠0, k≠0andl=0min{dtw(1, 1)k-1, l, dtw(1, 1)k, l-1, 　dtw(1, 1)k-1, l-1}+　d((l, i, o)k, (l, i, o)l), otherwise(2)

如果k, l同时为0, (t1)1和(t2)1中的三元组同时为空, 则距离函数dtw(1, 1) = 0; 如果k = 0且l ≠ 0, 或者k ≠ 0且l = 0, (t1)1和(t2)1中的三元组不同时为空, 则距离函数dtw(1, 1)为无穷大, 即dtw(1, 1) = ∞ 。如表2所示, (t1)1和(t2)1的距离dtw(1, 1) = ε +1。应用式(2)可计算t1与t2的距离, 如表3所示。

表2 计算(t1)1和(t2)1的距离 Table 2 Calculate the distance of (t1)1and (t2)1
表3 垂直维序列t1和t2的距离 Table 3 The distance of the vertical dimensional sequences t1and t2
2.2 计算垂直维序列间的距离

通过计算两棵广义树的垂直维序列的距离可以度量两棵广义树的相似度, 根据算法1, 度量两棵广义树的相似度等价于度量两个图的相似度。所以, 计算两个垂直维序列的距离可以度量两个图的相似度, 度量图的相似度问题简化为计算序列距离的问题。而计算两个垂直维序列的距离等价于计算它们结点序列三元组的距离。距离越小, 两个图的相似度越大; 反之, 两个图的相似度越小。因此, 本文提出了结合图顶点标号、入度和出度的动态时间规整方法, 通过计算两棵广义树的垂直维序列的距离度量两个图的相似度。

m = |t1|表示T1中垂直维序列数; n = |t2|表示T2中垂直维序列数, m ≥ 1, n ≥ 1, 垂直维序列(t1)u和(t2)v的距离函数记作dtw(u, v)。DTW(t1, t2)表示垂直维序列t1和t2距离函数, DTW(u, v)表示((t1)u, (t2)v)的距离, DTW(t1, t2)可以由DTW(u, v)递归计算得出, 0 ≤ u≤ m, 0≤ v≤ n, 结合式(2)有下式成立,

DTWu, v=0, ifu=0andv=0∞, ifu=0andv≠0, u≠0andv=0min{DTW(u-1, v), DTW(u, v-1), 　DTW(u-1, v-1)}+　dtw(u, v), otherwise(3)

如果u, v同时为0, t1和t2同时为空的序列, 则距离函数DTW(u, v) = 0; 如果u=0且v≠ 0, 或者u≠ 0且v = 0, t1和t2不同时为空, 则距离函数DTW(u, v)为无穷大, 即DTW(u, 0)=∞ 或DTW(0, v)=∞ 。

由表1可以得到, m = 5, n = 5, 根据式(3), 可递归地计算出DTW(u, v), 0≤ u≤ 5, 0≤ v≤ 5, 计算结果如表4所示。表4计算得到广义树T1和T2的距离为5ε +5, 所以应用垂直维序列的动态时间规整方法得到图G1和G2的度量结果为5ε +5。

表4 广义树T1和T2垂直维序列的距离 Table 4 The distance of vertical dimensional sequences between the generalized trees T1and T2

根据图顶点的入度和出度信息, 设置ε ≥ c, c为图中顶点的最大度数(包括入度和出度), 使在递归计算垂直维序列距离时, ε 始终大于两个顶点的入度差(i1- i2)和出度差(o1- o2), 简化了DTW((t1)u-1, (t2)v), DTW((t1)u, (t2)v-1)和DTW((t1)u-1, (t2)v-1)之间的比较。当参考值ε 出现, 表明在计算垂直维序列距离时结点的标号不同, 2ε 即为出现两次标号不同的情况, 3ε 即为三次标号不同的情况, 以此类推。

根据式(2)和式(3), 垂直维序列的动态时间规整算法的思想如下所示。

算法2 度量两个图G1和G2相似度的垂直维序列的动态时间规整算法

输入:图G1和G2

输出:图G1和G2的垂直维序列的距离

步骤1 应用算法1转换图G1和G2为垂直维序列t1和t2, t1和t2的结点用三元组(l, i, o)表示, m和n分别表示t1和t2的垂直维序列数, (t1)u表示t1中第u条序列, (t2)v表示t2中第v条序列, u ≤ m, v ≤ n。

步骤2 若u大于m, 转到步骤3。

步骤3 输出t1和t2的距离DTW(u-1, v-1)。

步骤4 若v大于n, 转到步骤5。

步骤6 应用式(2)和式(3)递归计算(t1)u和(t2)v的距离DTW(u, v), v = v+1, 转到步骤4;

步骤5 u=u+1, 转到步骤2。

DTW(u-1, v-1)可用于度量图G1和G2的相似度, 距离越小, G1和G2的相似度越大; 反之, 相似度越小。

算法2将度量图相似度问题简化为计算广义树垂直维序列距离的问题, 考虑了广义树根结点到叶子结点的顺序结构, 充分度量了图顶点的入度和出度信息, 有效地解决了度量图相似度过程中信息缺失的问题, 能够提高度量图相似度的准确性。

3 方法分析

根据算法1和算法2, 下面分析度量图相似度方法的时间复杂度。

定理1 V, E分别表示顶点带标号的有向图G的顶点集和边集, 则G转换为垂直维序列的时间复杂度为O(|V|+|E|)。

证明 图G转换为垂直维序列的时间复杂度可由算法1中得出。算法1的步骤6和步骤7为创建广义树的结点集和边集的过程, 时间复杂度为O(|V|); 步骤4和步骤8从广义树T中提取出垂直维序列, 这些操作可以在有限步骤下完成, 时间复杂度为O(1); 步骤3为根据两个顶点的边, 是否标记顶点的层, 执行判断(|E| = 0)的操作的时间复杂度为O(|E|)。因此, 将图转换为对应的垂直维序列的时间复杂度为O(|V|+O(1)+|E|), 近似为O(|V|+|E|), 得证。

定理2 T1和T2表示两棵广义树, t1和t2表示T1和T2的垂直维序列, m和n表示t1和t2中垂直维序列数, 则计算t1和t2距离的递归算法DTW(m, n)的时间复杂度为O(m× n× O(1))。

证明 从表3中看出, 垂直维序列的动态时间规整算法在计算dtw(u, v)的时构成m行n列矩阵, 其中1 ≤ u ≤ m, 1≤ v ≤ n。当u和v给定, dtw(u, v)等价于矩阵对应位置的元素值。而矩阵中的任一元素值, 可在有限的步骤下计算完成, 则计算dtw(u, v)的时间复杂度为O(1)。由式(3)得出, DTW(m, n)等价于矩阵Matrix(m, n), 其中Matrix(m, n)为Matrix第m行第n列的元素值。垂直维序列的距离可由矩阵中的元素值递归计算得出, 计算Matrix(m, n)的时间复杂度为O(m× n× O(1))。此外, DTW(m, n)的时间复杂度可由算法2中得出。首先, 在算法2的步骤6, 当u和v给定, 计算DTW (u, v)的时间复杂度为O(1); 其次, 由步骤2和步骤4得出, DTW(m, n)的时间复杂度为O(m× n)。因此, 通过分析算法2, DTW(m, n)的时间复杂度为O(m× n× O(1)), 得证。

算法2包括两部分:转换图G1和G2为垂直维序列t1和t2; 计算垂直维序列t1和t2间的距离。由定理1可知, G1和G2转换为t1和t2的时间复杂度为(O(|V1|+|E1|)+O(|V2|+|E2|)), 其中E1, E2分别为图G1和G2的边集, V1, V2分别为图G1和G2的顶点集; 由定理2可知, 计算t1和t2的时间复杂度为O(m× n× O(1)), 其中m, n分别为t1和t2的垂直维序列数。则有:

推论1 计算两个图的垂直维序列距离的时间复杂度为(O(|V1|+|E1|)+O(|V2|+|E2|)+O(m× n× O(1)))。

若|E1| = |V1|× (|V1|-1), |E2| = |V2|× (|V2|-1), 则G1和G2为完全有向图。根据定理1, 最坏情况下, 将G1和G2转换为对应的垂直维序列的时间复杂度为(O(|V1|+|V1|× (|V1|-1))+O(|V2|+|V2|× (|V2|-1)))。本文提出的垂直维序列的动态时间规整方法, 通过计算垂直维序列的距离度量图的相似度, 由推论2可知, 其时间复杂度是转换图为垂直维序列和递归地创建m行n列矩阵的操作数, 则有:

推论2 垂直维序列动态时间规整方法的时间复杂度为(O(|V1|+|V1|× (|V1|-1))+O(|V2|+|V2|× (|V2|-1))+O(m× n× O(1))), 近似为O(n2)。

与现有的图相似度度量方法相比, 本文方法具有低的时间复杂度O(n2)。表5列举本文方法与现有方法的时间复杂度的对比。

表5 不同图相似度度量方法的时间复杂度 Table 5 The time complexity of different graph similarity methods
4 结束语

本文首先等价地转换图为广义树, 其次表示广义树为垂直维序列, 最后通过计算垂直维序列的距离度量图的相似度, 将度量图相似度简化为计算垂直维序列的距离。与现有方法相比, 垂直维序列体现了图的层次结构特性, 垂直维序列的动态时间规整方法充分考虑了图顶点的入度和出度信息, 解决了在度量图相似度过程中信息缺失的问题, 保证了度量的准确性, 且具有低的时间复杂度O(n2)。

The authors have declared that no competing interests exist.

参考文献
[1] Ahmed A, Shervashidze N, Narayanamurthy S, et al. Distributed large-scale natural graph factorization[C]∥22nd International Conference on World Wide Web, Rio de Janeiro, Brazil, 2013: 37-48. [本文引用:1]
[2] Shanavas N, Wang H, Lin Z, et al. Supervised graph-based term weighting scheme for effective text classification[C]∥Proceedings of the 22nd European Conference on Artificial Intelligence, Hague, Netherland s, 2016: 1710-1711. [本文引用:1]
[3] Macropol K, Singh A. Reachability analysis and modeling of dynamic event networks[C]∥European Conference of Machine Learning and Knowledge Discovery in Databases, Bristol, UK, 2012: 442-457. [本文引用:1]
[4] Sugiyama M, Llinares F, Kasenburg N, et al. Significant subgraph mining with multiple testing correction[C]∥Proceedings of the SIAM International Conference on Data Mining, Vancouver, Canada, 2015: 37-45. [本文引用:1]
[5] Vishwanathan S, Schraudolph N, Kondor R, et al. Graph kernels[J]. Journal of Machine Learning Research, 2010, 11: 1201-1242. [本文引用:1]
[6] Sugiyama M, Borgwardt K. Halting in rand om walk kernels[C]∥28th International Conference on Neural Information Processing Systems, Montreal, Canada, 2015: 1639-1647. [本文引用:1]
[7] Borgwardt K, Kriegel H. Shortest-path kernels on graphs[C]∥Proceedings of IEEE International Conference on Data Mining, Houston, USA, 2005: 74-81. [本文引用:1]
[8] Elzinga C, Wang H. Kernels for acyclic digraphs[J]. Pattern Recognition Letters, 2012, 33(16): 2239-2244. [本文引用:1]
[9] Forster D, Bittner L, Karkar S, et al. Testing ecological theories with sequence similarity networks: marine ciliates exhibit similar geographic dispersal patterns as multicellular organisms[J]. BMC Biology, 2015, 13: doi: DOI:10.1186/s12915-015-0125-5. [本文引用:1]
[10] Yanardag P, Vishwanathan S. A structural smoothing framework for robust graph comparison[C]∥Proceedings of Neural Information Processing Systems, Montreal, Canada, 2015: 2134-2142. [本文引用:1]
[11] Shervashidze N, Schweitzer P, Leeuwen E, et al. Weisfeiler-Lehman graph kernels[J]. Journal of Machine Learning Research, 2011, 12: 2539-2561. [本文引用:1]
[12] Yanardag P, Vishwanathan S. Deep graph kernels[C]∥Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 2015: 1365-1374. [本文引用:1]
[13] Sakoe H, Chiba S. Dynamic programming algorithm optimization for spoken word recognition[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1978, 26(1): 43-49. [本文引用:1]
[14] Kurbalija V, Radovanovic M, Geler Z, et al. The influence of global constraints on similarity measures for time-series databases[J]. Knowledge-Based Systems, 2014, 56: 49-67. [本文引用:1]
[15] Wang Q, Korkin D, Shang Y. A fast multiple longest common subsequence(MLCS) algorithm[J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(3): 321-334. [本文引用:1]
[16] Wang H. All common subsequences[C]∥Proceeding 20th International Joint Conference on Artificial Intelligence, Hyderabad, India, 2007: 635-640. [本文引用:1]
[17] Lin Z, Wang H, McClean S. A multidimensional sequence approach to measuring tree similarity[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(2): 197-208. [本文引用:1]
[18] Li Tao, Dong Han, Shi Yong-tang, et al. A comparative analysis of new graph distance measures and graph edit distance[J]. Information Sciences, 2017, 403: 15-21. [本文引用:1]
[19] Zhu Gang-gao, Iglesias C. Computing semantic similarity of concepts in knowledge graphs[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(1): 72-85. [本文引用:1]