在DRGS中, 交通信息具有动态的特性, 即权值随时间发生变化; 另一方面, 随着车辆不断行驶, 起始点不断变化。在基于图论的基础上, 结合其动态特性, 动态路径优化问题可形式化为:

P=S, A, wij, Sstrat, Sgoal(1)

式中:(S, A)为搜索空间, S为状态空间中所有可获取的结点, A为状态空间中所有弧, 每条弧(i, j)间权重为w_ij; S_start、S_goal 分别为优化问题的起始点、目标点, 其中, S_start、w_ij随时间发生变化。

路径选择模型是路径优化算法的基础, 它可以提供交通网络的参数变化, 从而为路径优化算法提供必要的基础数据支持。为简化处理问题, w_ij权值为车辆行驶时间。在最短路径的数学模型的基础上, 结合图论相关知识及动态路径诱导问题, 得到基于时间最短的路径选择模型为:

min∑i=SstartSgoali∈S∑j∈SSgoali≠jwijtγij(2)

γij=1, (i, j)∈A(Sstart, Sgoal)0, (i, j)∉A(Sstart, Sgoal)(3)

式中: wijt表示在t时间段内行驶路段(i, j)间所需时间。式(3)为无环路约束因子, 即当前路段(i, j)∈ A时, 系数为1; 否则为0。

粒子群优化算法源于解决非线性连续问题, 具有收敛快、参数精简等优点。近些年, PSO被广泛应用于离散组合优化问题^[13], 其处理策略一般是采用离散问题连续化^[14]。Goksal等^[15]针对同步收集与配送VRP问题, 采用置换编码连续化VRP, 并结合变领域下降(Variable neighborhood descent, VND)策略求解。但动态路径优化与VRP有所差异:

(1)结束条件:动态路径优化是以目标点为结束条件; VRP则以所有节点加入子回路时结束。

(2)结构:动态路径优化问题是以加权有向图为理论基础^[6], 而VRP是以强连通图为基础^[2], 以某种编码连续化问题, 组合所有节点得到最优解。而且, 在实时环境下, 动态路径优化问题具有实时特性^[7], 且交通路网庞大, 因此, 以类似于VRP的PSO算法解决动态路径优化问题并不实用。

为进一步验证结论, 假设路网节点个数为N, 若以类似于VRP的PSO算法解决动态路径优化问题, 则当前路网结构中有N(N-1)/2条边(以无向图为前提); 然而, 根据我国城市路网连接度系数J值, 其分布为3.2~3.9^[16], 因此, 实际路网结构最多有1.95N条边。显然, PSO优化算法以类似于VRP的方式应用于DRGS, 其时间和空间复杂度均明显增加, 无法满足实时性。然而, 在实时环境下, 信息具有动态性, PSO算法以局部最优、全局最优的智能存储方式适用于动态环境。

在智能交通中, PSO算法以局部最优实现解更新, 并以局部最优为剪枝算法的阈值; 全局最优解则记录实际行驶路径。其局部最优、全局最优形式化表达如式(5)(6)所示:

Plocal=localij|i, j∈S, A(5)

Pglobal=globalij|i, j∈S, A(6)

模糊时间窗是利用当前路段行驶的时间约束算法优化周期, 模糊时间窗形式化为:

aij=0, localij(7)

式中:(i, j)表示当前路段, local_ij为车辆行驶当前路段所需时间。基于模糊时间窗下, 算法优化时间a_ij在时间窗[0, local_ij )范围内, 因此, a_ij小于local_ij。

广义自适应A^* 算法被认为是A^* 算法的迭代过程, 但区别于此过程。s_start更新时, 若启发值一致性未变化, 即在当前最优解不变的情况下, 则不调用A^* 算法。同样, 在混合算法中不调用优化算法。

混合算法是在广义自适应A^* 算法的基础上, 结合剪枝策略, 同时引入PSO局部最优、全局最优、模糊时间窗的优化策略。在智能交通系统中, 动态路径优化算是在实时环境下的寻优过程, 因此, 算法分为仿真线程和主线程, 仿真线程实现实时信息更新; 而主线程完成寻优过程。

2.1.1 仿真线程

在仿真线程中, 以计时器1计时的方式更新数据。当计时器1计时为t秒时, 进一步判断两个线程是否发生冲突, 即数据竞争。当两个线程间共享数据的非同步访问导致数据竞争时, 易产生不确定性的结果。因此, 采用互斥量及线程休眠方式避免数据竞争。当线程被重新唤醒时, 执行数据更新过程。

2.1.2 主线程

Step1 初始化:S_start、S_goal, 加载S_start和S_goal间地图信息及当前实时信息w_ij, 调用A^* 算法初始化P_local、P_global、a_ij, 执行Step2。

Step2 计时器2对当前a_ij下算法优化时间进行计时。当计时器2与a_ij相等时, 则更新S_start, 同时更新P_local、P_global、以及a_ij, 计时器2归零; 否则, 判断S_start与 S_goal是否相等, 若S_start!= S_goal, 执行Step3。当S_start= S_goal时, 计数器₁归零, 仿真线程结束, 同时主线程结束。

Step3 判断观察函数的返回值, 当返回值为1时, 调用优化算法, 执行Step2。

在算法主体中, 优化算法和观察函数是解决动态路径优化问题的关键。

(1)优化算法完成寻优过程, 优化算法在广义自适应A^* 算法基础上, 结合剪枝策略实现求解过程。A^* 算法求解最优路径问题过程如下:

假设当前节点为S_i、起始点到节点i的代价为C(S_start, i)、节点i到节点j间的代价为cost_ij、优先队列为Q、前驱列表为Path_i、评估函数为F(i)=C(S_start, i)+E(i, S_goal), 其中, E(i, S_goal)为当前节点i到目标节点的估计值。

Step1 初始化S_i、C(S_start, i)=0、C(S_start, j)=∞ 、Path_i=NULL, 符合扫描条件的节点集Q={ Si}, 执行Step2。

Step2 选择节点, 在Q集合选择并删除当前节点i, 执行Step3。

Step3 扩展当前节点i下所有子节点, 对于每条弧A_ij, 如果满足C(S_start, i)+cost_ij+ E(i, S_goal)< F(j), 则C(S_start, j)= C(S_start, i)+ cost_ij; F(j)=C(S_start, i)+ cost_ij+ E(i, S_goal); Path_i= A_ij, 节点j插入Q, 执行Step4。

Step4 如果Q=⌀, 程序结束; 否则执行Step2。

在启发式最短路径中, A^* 算法和剪枝算法同属于限制搜索区域的优化算法, 但剪枝算法是以阈值限制搜索区域。其阈值为P_local, 提高搜索效率的同时避免收敛过早。在A^* 算法的基础上, 在Step2中采用剪枝策略, 其改进过程如下:

Step2 选择节点, 在Q队列中优先选择最小代价的节点, 假设为i, 如果C(S_start, i)+ E(i, S_goal)> P_local, 则执行上述Step4, 否则执行Step3。

(2)观察函数针对动态信息的检测, 并结合广义自适应A^* 算法完成动态信息的处理过程。仿真线程更新数据后, 执行观察函数, 针对不同的变化, 观察函数反馈不同的结果, 其结果有以下几种类型:

(a)返回结果为0时, 即数据更新后, w_ij未发生变化, 则程序等待仿真线程执行更新数据;

(b)返回结果为1时, 表示数据更新后, w_ij发生变化且当前路径未发生变化或局部最优解增大, 则更新P_local, 并设置P_local为剪枝算法的阈值, 调用优化算法。若发生剪枝, 则表示当前P_local是当前信息下最优解, 则仅更新P_local值; 反之, 优化算法得到当前信息下的最优路径, 则重构P_local;

(c)返回结果为2时, 即数据更新后, w_ij减小且为当前局部最优解减小, 则仅更新P_local值。

2.2.1 基于PSO算法的应用

在算法中, 局部最优及全局最优的应用如下:

(1)作为剪枝算法的阈值, 有效限制搜索区域, 同时避免过早收敛;

(2)在观察函数中, 判断w_ij是否发生变化, 当w_ij减小且发生在局部最优, 则无需调用优化算法重构P_local, 仅更新P_local值即可。因此, 提高算法的运行速率; 当w_ij未发生变化, 同样, 无需调用优化算法, 等待仿真线程更新数据;

(3)出行车辆在行驶的过程中, 起始点S_start不断发生变化, S_start不断添加到全局最优P_global中, 当S_start=S_goal时, 得到全局最优解。

2.2.2 模糊时间窗的应用

算法优化时间采用模糊时间窗约束取代迭代控制的策略。在基于模糊时间窗约束下, 算法中采用计时器与模糊时间窗相比较的方式:当两者相等时, 更新S_start, 同时更新a_ij, 即当前起始点下, 算法可在a_ij时间窗内优化未行驶路径; 当S_start与实时数据同时更新时, 实时数据更新过程则采用线程休眠的方式, 即w_ij等待更新。采用休眠更新w_ij的原因在于:一方面, 符合智能交通中动态路径诱导的意义; 另一方面, 模糊时间窗作为算法优化时间的约束, 要求算法运行时间控制在模糊时间窗内。

到目前为止, 实验数据没有统一标准。为验证算法, 实验数据源于离散数学与理论计算研究中心(http:∥www.dis.uniroma1.it/challenge9/download.shtml)。New York Road数据集为美国纽约市路网结构图, 包括静态数据(坐标及距离)和动态数据(时间), 但动态数据单一化。该测试集的经纬度为[40° 3'N, 41° 3'N], [73° 5'W, 74° 5'W], 以无向图统计:节点为264 346个, 弧为366 923条。结合交通信息动态、随机、不确定的特性, 动态数据以随机化方式生成5个行驶时间样本, 并采用定时更新模拟实时环境。

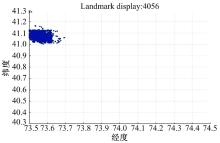
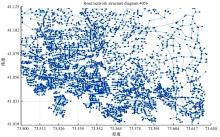
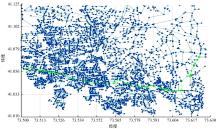
由于测试集数据庞大, 为适应仿真环境, 提取该数据集中部分数据, 包括4056个节点和5287条边。该测试集连接度指数J约为2.776, 相比提取数据集的J值约为2.607。比较J值可知:提取数据集的J值略小于纽约市路网的J值, 但满足于需求, 图形化提取测试集节点分布以及路网结构如图1、图2所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 节点分布Fig.1 The distribution of nodes

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 路网结构Fig.2 The structure of road

图1是提取的测试集经纬度范围为 [73° 5'W, 74° 5'W]、 [40° 3'N, 41° 3'N]; 图2是基于提取的4056个节点下, 10 574条路段构成的路网结构。由图示可知:提取的4056个节点分布相对集中, 且路网结构复杂, 与实际中路网结构具有相似性, 因此, 可作为实验测试集。为进一步验证数据, 分别针对有效性和合理性进行了分析证明。有效性是验证数据集合中路径存在率; 合理性是验证其动态特性, 即基于不同实时信息下, 同一起始点与目标点间的路径具有多样性的特性。针对路径存在率以距离为权重随机化S_start、S_goal, 分别迭代100、1000、10 000次的求得最短路径的次数, 其结果如表1所示。

表1

Table 1

表1(Table 1)

表1 合理性验证 Table 1 Reasonableness verification 迭代次数 100 1000 10000 存在率/% 95 95.3 95.66

表1 合理性验证 Table 1 Reasonableness verification

分析表1可知:测试集合中两点间路径存在率大于95%, 因此, 实验数据具有一定的合理性。

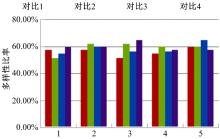
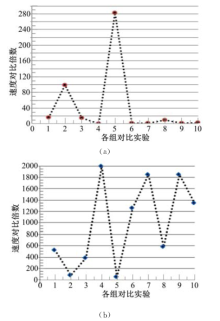
同时, 针对多个时间测试集合的数据间进行多样性验证, 即随机化S_start、S_goal迭代10 000次情形下, 统计两两测试集合间相异次数。在路径存在率的基础上, 计算相异次数与其存在路径次数的比值, 并作为测试集合间的多样性比率。当各个测试集合间的多样性比值越大, 路径的多样性越多, 越符合智能交通中信息的动态性, 其多样性比值统计结果如图3所示, 对比1、2、3、4表示除横坐标时间测试集外其他各个测试集。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 多样性统计Fig.3 Diversity statistics

由图3可知:各个测试集合间的多样性比值均在50%~70%之间, 因此, 基于实时环境下, 各个时间测试集合间具有一定的动态特性。

优化算法在广义自适应A^* 算法的基础上, 结合剪枝算法, 实现了基于混合的动态路径优化算法。同时, 采用PSO算法中局部最优以及全局最优解的策略适应智能交通中信息的动态性, 且算法以模糊时间约束算法优化时间。为验证算法, 分别从以下方面进行实验:

(1)在实时环境下, 验证优化策略的有效性以及合理性。

(2)优化算法与A^* 算法在运行时间上进行对比。

在仿真实时环境下, 反复实验的基础上, 选取一组为实例分析并列举了多组对比实验。实验数据采用上述实验测试集, 并在仿真线程中每5 s更新一次数据。为验证算法性能, 将优化算法与A^* 算法进行了对比实验。为形象地显示实验结果, 分别以图示及评价参数表格进行对比分析。

3.3.1 实例分析算法性能

在仿真实时环境下, 以起始点100到目标节点4056为一组实例进行分析。为验证节点100~4056解的多样性, 依次得到测试集1、2、3、4、5的基于时间最短的最优路径如图4所示, 其中红、黄、白、紫、绿色路径分别表示时间测试集1、2、3、4、5下的最优路径。

图4

Fig.4

	Figure Option ViewDownloadNew Window
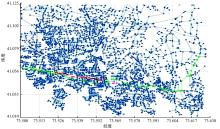	图4 基于5个时间测试集下节点100到节点4056最优路径Fig.4 The optimal path from node 100 to node 4056 based on 5 time test sets

由图4可知:有红、黄、紫、绿4种颜色, 则说明在不同测试集下有不同的最优路径, 即节点100~4056, 在不同测试集下有4种不同的最优路径, 而图中没有白色显示, 则说明当前测试集下的最优路径与其后的最优路径重合, 即测试集3下的最优路径被测试集4、5覆盖。为进一步分析, 分别得到5个测试集的最优解如表2所示。

表2

Table 2

表2(Table 2)

表2 测试集的最优解 Table 2 The optimal solution of test set 测试集合 最优解/ms 节点数/个数 1 229 471 122 2 229 028 108 3 233 985 108 4 232 603 108 5 236 213 113

表2 测试集的最优解 Table 2 The optimal solution of test set

由表2可知:5个测试集的解均不一样, 但由图4可知, 在5个测试集下节点100~4056的最优路径仅有4条。由表中节点数可知:2、3、4测试集的节点数相同, 进一步分析, 由图4可知, 测试集3的最优路径与其后的测试集重合, 因此, 可得出测试集3与测试集4的最优路径相同, 但最优解不同。这种情况是由于实时环境下, 同一条路径下, 其值大小有所差异。

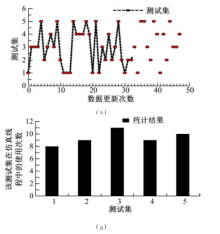
基于上述实验的基础上, 在仿真线程中, 数据一共更新47次。为简化实验并达到实验目的, 将车辆的运行时间与仿真时间之间进行了转换处理, 即运行时间1000 s等价于仿真时间的1 s。其数据随时间更新过程及测试集分布统计结果如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 仿真实验环境Fig.5 Simulation experiment environment

在图5(a)中, 图中实心圆点表示当前仿真数据所处的测试集中, 为更清晰显示数据随时间的变化过程, 以虚折线描述该过程。而图5(b)是对图5(a)数据分布的统计结果。

基于上述仿真环境下, 优化算法与A^* 算法的对比结果如图6、图7所示。图6是算法第一次调用A^* 算法得到的局部最优路径; 图7是在动态信息下, 调用优化算法得到的局部最优路径; 黑色矩形框为出行者行驶过的路径。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 A* 算法的最优路径Fig.6 A* algorithm to solve the optimal path

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 本文优化算法的最优路径Fig.7 Optimization algorithm to solve the optimal path

由图6、图7可知:两图局部最优路径相同, 源于剪枝策略。当实时数据更新后, 更新局部最优解, 并以此为阈值限制算法的搜索区域。当发生剪枝时, 优化算法寻优过程结束, 则当前局部最优即为当前最优路径。为进一步验证算法的性能, 分别在运行时间、最优解、节点个数等参数上进行了对比实验, 其结果如表3所示。

表3

Table 3

表3(Table 3)

表3 对比实验结果 Table 3 The comparison of experimental results 算法 时间/ms 局部最优/ms 节点/个数 A* 26 424 229 471 122 优化 1553 228 468 119

表3 对比实验结果 Table 3 The comparison of experimental results

由表3可知:在同等测试集下, 优化算法的运行速率是A^* 算法的13倍, 甚优于A^* 算法。算法初始化时, 实时环境为初始态, 由图5可知:当前测试集为1。调用A^* 得到局部最优解, 其解值为229 471。由表2可知:测试集1下最优解值为229 471, 因此, 局部最优解与测试集1最优解相同。当黑色矩形区域行驶完成后, 所用时间为8289 s, 则当前局部最优解为221 182 s。在当前起始点下, 观察函数的返回结果为1, 调用优化算法, 得到局部最优解为228 468 s。优化算法的局部最优解大于A^* 算法, 其原于实时信息下, 导致局部最优解增大。在执行A^* 算法时实时环境为测试集1, 而由图5可知:执行优化算法时实验数据为测试集3。且由上述分析可知:在优化算法中发生剪枝, 则原路径即为测试集3下的最优路径。但测试集3下的最优解值远大于测试集1, 因此, 局部最优解增大。A^* 算法的最优路径节点个数为122, 优化算法的节点个数为119, 则两者相差3个节点, 即为图7矩形框内的节点。

3.3.2 实例分析优化策略

为验证优化策略的合理性, 针对PSO局部最优及全局最优智能存储方式以及模糊时间窗进行了实验。由于以局部最优为剪枝算法的阈值, 当观察函数检测到当前路径减少或者有折回现象时, 仅更新局部最优解而无需调用优化算法。因此, 基于局部最优优化策略下, 算法的运行时间均在4 ms左右, 运行速率明显优于优化算法。因此, 在混合优化算法中引入局部最优是有效的。

全局最优解是一个逐步求解的过程, 全局最优解随起始点变化而变化, 直到到达目标节点。基于上述求解过程, 全局最优解为233 836 s。在仿真线程中, 数据更新了47次, 则47× 5 s× 1000=235 000 s接近于车辆行驶时间23 2300 s, 因此, 模糊时间窗在控制仿真时间是有效的。由表3可知:1、2测试集最优解优于全局最优, 而3、4、5劣于全局最优。进一步结合测试集分布情况可知:测试集1、2共执行了17次, 则3、4、5测试集共执行了30次。由此可见, 全局最优解是有效的, 全局最优路径如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 全局最优路径Fig.8 Global optimal path

3.3.3 多组对比实验

为进一步验证算法的性能, 列举10组对比实验, 且每组实验测试20次求均值, 统计结果如表4所示。

表4

Table 4

表4(Table 4)

表4 10组20次实验均值统计结果 Table 4 Statistical results of 20 experiments in 10 groups 序号 起始节 点编号 目标节 点编号 A* 算法 /ms 优化算法 /ms 优化策 略/ms 1 3914 3582 10900.1 109.5 1.4 2 800 1890 23417.2 1613.7 4.2 3 645 3678 15378.3 12593.6 3.3 4 394 3340 32087.4 1 2.2 5 1808 2622 6193.8 3655.5 2.9 6 929 3705 23989.1 17872.5 3.8 7 2184 4041 16856.2 11282.4 3.6 8 1750 3694 14196 1517.6 2.6 9 1711 3715 14050.1 10703.6 3.8 10 1544 2304 6005.5 2163.2 1.6

表4 10组20次实验均值统计结果 Table 4 Statistical results of 20 experiments in 10 groups

10组对比结果统计如图9所示, 图9(a)为A^* 算法与优化算法运算速率比值统计结果, 图9(b)为优化算法与优化算法中引入优化策略的运算速率比值的统计结果。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 对比实验统计结果Fig.9 The contrastive experiment result

由图9可知:优化算法的运算速率均优于A^* 算法, 比值分布在不同区间。由于算法是基于广义自适应A^* 算法的基础上结合剪枝算法的优化算法, A^* 算法中以优先队列Q存储待扩展节点, 并以剪枝阈值为结束条件之一, 进而加快算法运算速率。相比优化算法与优化策略速率比值可知:引入优化策略后, 算法运行速率均甚优于优化算法, 原于优化策略适应于实时环境。基于上述优化策略, 在观察函数中, 判断当前起始点S_start下的w_ij是否发生变化:当w_ij减小且发生在局部最优解, 则无需调用优化算法重构最优路径, 仅需修改P_local值, 因此节省大量运行时间; 当w_ij未发生变化, 同样, 无需调用优化算法, 等待仿真线程更新数据。因此, 优化策略可有效避免调用优化算法, 提高算法运行效率, 从而更好的适应动态实时环境。因此, 进一步证明了优化策略的有效性。