基于增强核极限学习机的专业选择智能系统

引用本文

黄辉, 冯西安, 魏燕, 许驰, 陈慧灵. 基于增强核极限学习机的专业选择智能系统[J].吉林大学学报（工学版）, 2018,48(4): 1224-1230
HUANG Hui, FENG Xi-an, WEI Yan, XU Chi, CHEN Hui-ling. An intelligent system based on enhanced kernel extreme learning machine for choosing the second major[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 1224-1230 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170307
Permissions

基于增强核极限学习机的专业选择智能系统

黄辉^1,², 冯西安¹, 魏燕³, 许驰³, 陈慧灵²

1.西北工业大学航海学院,西安 710072

2.温州大学数理与电子信息工程学院,浙江温州 325035

3.温州科技职业学院信息技术学院,浙江温州 325006

通讯作者:魏燕(1983-),女, 高级工程师.研究方向:信息系统,数据挖掘.E-mail:weiyan@wzvcst.edu.cn

作者简介:黄辉(1982-),男, 实验师, 博士研究生.研究方向:图像处理,机器学习.E-mail:huanghui@wzu.edu.cn

基金:国家自然科学基金项目(61101155); 浙江省自然科学基金项目(LY15F020033); 温州市科技计划项目(2016R0002); 浙江省教育厅科学研究基金项目(Y201533884); 浙江省科技计划项目(2014C32031).

摘要

基于粒子群优化(PSO)的增强型核极限学习机(KELM)提出了一种有效的预测模型PSO-KELM来辅助第二专业选择。在PSO-KELM 中,PSO策略确定KELM的最佳参数。PSO-KELM与其他两个竞争方法在学生专业选择数据上通过10折交叉验证方案进行比较,这两个方法分别是支持向量机和网格搜索技术优化的KELM。结果表明了本文预测模型在分类精度、受试者工作特征曲线面积(AUC)、灵敏度和特异性方面的优越性。

关键词: 计算机应用; 核极限学习机; 粒子群优化; 第二专业选择

中图分类号:TP393 文献标志码:A 文章编号:1671-5497(2018)04-1224-07

An intelligent system based on enhanced kernel extreme learning machine for choosing the second major

HUANG Hui^1,², FENG Xi-an¹, WEI Yan³, XU Chi³, CHEN Hui-ling²

1.School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China

2.College of Mathematics, Physics and Electronic Information Engineering, Wenzhou University, Wenzhou 325035, China

3.Wenzhou Vocational College of Science and Technology, Wenzhou 325006, China

Abstract

This paper proposes an effective prediction model for choosing the second major based on the Particle Swarm Optimization (PSO) enhanced Kernel Extreme Learning Machine (KELM), which is called PSO-KELM model. In this model, the PSO strategy is adopted to adaptively determine the optimal parameters in KELM. The PSO-KELM model is compared with other two competitive methods, including Support Vector Machine (SVM) and a KELM is optimized by grid search technique, on a major selection dataset via a 10-fold cross validation scheme. The results clearly confirm the superiority of the proposed PSO-KELM model in classification accuracy, area under the receiver operating characteristic curve (AUC), sensitivity and specificity.

Keyword: computer application; kernel extreme learning machine; particle swarm optimization; second major selection

文章图片

0 引言

目前, 数据挖掘技术在高等教育教学领域中的应用逐渐受到重视, 在学生选课、成绩预测、职业指导等方面已经有较多的应用。Kardan等^[1]探讨了在网络学习背景下通过数据挖掘技术来预测学生课程选择的情况。Guo^[2]提出用统计分析和神经网络建立动态模型来分析和预测学生的课程满意度。结果表明, 在预测学生课程满意度时, 多层感知器模型优于线性回归分析。Campagni等^[3]提出了一种基于聚类和序列模式的高校毕业生职业生涯分析方法, 有助于研究生职业生涯规划。Huang等^[4]分析了统计学、心理学等评价理论, 提出了基于粗糙集的关联规则挖掘算法来进行第二专业选择。仿真结果表明, 他们的方法在软件工程、网络技术、程序设计3个专业的评测上具有较高的精度。

为了提高学生第二专业选择的效率, 本文提出并验证了一种基于粒子群增强的核极限学习机(Particle swarm optimization enhanced kernel extreme learning machine, PSO-KELM)方法。核极限学习机是在极限学习机(Extreme learning machine, ELM)^{[5, 6]}基础上发展而来的, 是一种新的单隐层的前馈神经网络的学习算法。作为ELM的扩展, KELM克服了ELM由于随机权重导致的在不同试验中产生不同性能的缺点, 由于其良好的性能, KELM具有广泛的应用, 包括高光谱遥感影像分类、动作识别、二维轮廓重建、生物引擎性能优化、疾病诊断、故障诊断和破产预测等。目前, KELM尚未被应用于学生第二专业选择。一些研究^{[7, 8, 9]}表明, KELM中的一些参数(如惩罚参数 $C 和核宽度 γ)$ 对模型的性能具有显著的影响, 因此, 本文提出一种群智能技术用于解决KELM模型的参数优化问题, 类似于支持向量机(Support vector machines, SVM)^{[10, 11]}和随机森林(Random forest)^[12]的参数优化方法。经典的粒子群(Particle swarm optimization, PSO)优化策略, 由于其易实现和良好的性能被考虑用于KELM模型的参数调整, 通过运行于温州科技职业学院收集的实际数据, 将PSO-KELM模型与支持向量机(SVM)和基于网格的KELM(grid-KELM)模型进行了严格的比较, 包括各种分类器的分类准确率(ACC)、ROC曲线下面积(AUC)、灵敏度(Sensitivity)和特异性(Specificity)等指标。实验结果表明, 本文PSO-KELM方法比其他两种先进的机器学习算法具有更好的性能。

1 预测模型的建立

面向第二专业选择系统基于KELM构造, 其中输入数据是由一系列影响专业选择的因子组成, 在输入空间中的数据利用RBF核^[13]映射到隐藏层的特征空间; 最优惩罚参数 $C 和核宽 γ$ 由PSO算法动态指定, 一旦通过训练阶段得到最优参数对, 将送入KELM模型中执行预测任务。构建的模型框架如图1所示。

	Figure Option View Download New Window
	图1 基于粒子群优化的核极限学习机预测模型Fig.1 KELM prediction model based on PSO

在PSO-KELM预测模型中, PSO优化KELM参数的步骤如下:

步骤1 初始化如下PSO算法参数:种群规模(pop)、最大迭代次数(maxi)、粒子位置(pos)、粒子速度(vel)和适应度(fit)。

$x_{i, j} = x_{\min} + r_{1} \times (x_{\max} - x_{\min});$

$v_{i, j} = v_{\min} + r_{2} \times (v_{\max} - v_{\min});$

式中: $x_{i, j}$ 表示粒子当前位置; $v_{i, j}$ 表示粒子当前速度; $x_{\min}$ 和 $x_{\max}$ 分别为位置的最小值和最大值; $v_{\min}$ 和 $v_{\max}$ 分别为速度的最小值和最大值; $r_{1} 、 r_{2}$ 均为随机数。

步骤2 设置维度( $\dim$ )和当前迭代次数( $iter$ ), 令 $\dim = 2, iter = 1 。$

步骤3 将pos和fit赋值给局部最优位置( $lpos$ )和局部最优适应度(lfit), 即 $pos = pos, lfit = fit 。$

步骤4 将最大的 $lfit$ 作为全局最优适应度( $gfit$ )并返回对应的粒子编号 $index$ , 即 $[maxlfit, index] = Max (lfit)$ , gfit=maxlfit。

步骤5 将具有 $gfit$ 的 $lpos$ 作为全局最优位置( $gpos$ ), 即 $gpos = lpos (index) 。$

步骤6 更新 $iter, 令 iter = iter + 1 。$

步骤7 更新 $pos 、 vel$ 和 $fit$ , 其中w是惯性因子; $c_{1} 、 c_{2}$ 为加速常数。

$\begin{array}{l} v_{i, j}^{n + 1} = w \times v_{i, j}^{n} + c_{1} \times r_{1} (p_{i, j}^{n} - x_{i, j}^{n}) + \\ c_{2} \times r_{2} (p_{g, j}^{n} - x_{i, j}^{n}) \end{array}$

$w = w_{\min} + (w_{\max} - w_{\min}) \frac{(t_{\max} - t)}{t_{\max}}$

If $(v_{i, j}^{n + 1} \notin [v_{\min}, v_{\max}]),$ then

$v_{i, j}^{n + 1} = \max (\min (v_{\max}, v_{i, j}^{n + 1}), v_{\min})$

End If;

$x_{i, j}^{n + 1} = x_{i, j}^{n} + v_{i, j}^{n + 1}, j = 1, 2, \dots, d$

If $(x_{i, j}^{n + 1} \notin [x_{\min}, x_{\max}]),$ then $x_{i, j}^{n + 1} = \max (\min (x_{\max}, x_{i, j}^{n + 1}), x_{\min})$

End If;

步骤8 通过比较 $fit$ 和 $lfit$ 更新 $lfit$ 和 $lpos$ 。

步骤9 通过比较最大的 $lfit$ 和 $gfit$ 更新 $gfit$ 和 $gpos$ 。

步骤10 判断 $iter$ 是否达到 $maxi$ , 如果是, 则算法结束, 输出 $gpos$ ; 否则, 返回步骤6。

步骤11 将 $gpos$ 的第一维位置作为参数C的值, 第二维位置作为参数 $γ$ 的值, $bestC = gbest (1); bestγ = gbest (2)$ 。

2 实验设计

2.1 数据描述

本研究所获得的数据来自温州科技职业学院, 以数字媒体专业三届共402位学生作为研究对象。该专业分为平面设计和影视制作两个专业方向。在第二学期结束后, 195位学生选择了平面设计专业方向, 207位学生选择了影视制作专业方向。本研究通过对学生性别、高考生类别、区域生源、文理科情况、志愿情况、基础课成绩、第三课堂参加情况、自考学习情况、专业方向关联基础课成绩等11个特征属性进行挖掘分析, 了解各属性的重要性及属性之间潜在的内在联系, 为实验准备必要的数据。表1为11个特征属性的具体描述。

表1 特征属性描述 Table 1 Description of data set

2.2 实验设置

为了验证本文PSO-KELM算法, 将该算法与其他两种高效的机器学习算法Grid-KELM和SVM进行对比。对于SVM, 利用文献[14]中实现的算法LIBSVM。数据在分类之前, 被缩放到[-1, 1]内, 实验环境基于AMD Athlon 64 X2双核处理器(2.6 GHz)和4 GB内存, 运行在Windows 7操作系统上。

k折交叉验证(CV)用于验证分类的性能来保证结果的无偏差, PSO-KELM的参数设置如下:迭代次数和粒度分别设置成100和25; 参数搜索范围: $C \in {2^{- 5}, 2^{- 3}, \dots, 2^{15}}, γ \in {2^{- 15}, 2^{- 13}, \dots, 2};$ 对连续维度来说, 粒子群PSO的最大速度v_max设置为每维的60%; $c_{1 i} = 2.5, c_{1 f} = 0.5, c_{2 i} = 0.5, c_{2 f} = 2.5; w_{\max} 和 w_{\min}$ 分别设置成0.9和0.4。

2.3 性能评估方法

为了评价面向第二专业选择的PSO-KELM算法, 本文主要考查4个指标:分类准确率(ACC)、ROC曲线下面积(AUC)、灵敏度(Sensitivity)和特异性(Specificity)。性能指标计算公式如下:

$ACC = \frac{TP + TN}{TP + FP + FN + TN} \times 100 %$ (1)

$Sensitivity = \frac{TP}{TP + FN} \times 100 %$ (2)

$Specificity = \frac{TN}{FP + TN} \times 100 %$ (3)

$AUC = (Sensitivity + Specificity) / 2$ (4)

式中: $TP$ 是真阳性的数量, 即专业‘ A’ 被正确分类的次数; $FN$ 是误报的数量, 即专业‘ A’ 被分类成专业‘ B’ 的次数; $TN$ 是真阴性的数量, 即专业‘ B’ 被正确分类的次数; $FP$ 是假阳性的数量, 即专业‘ B’ 被分类成专业‘ A’ 的次数。

ROC曲线是一种图像化显示方法, 用于衡量Logistic模型的预测精度, 曲线显示模型的真阳性和假阳性率; AUC是ROC曲线下的面积, 是用来比较分类器在二分类问题上性能的最佳方法之一。

3 实验结果与分析

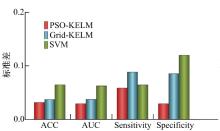
在该实验中, 本文评估了PSO-KELM模型在原始特征空间的有效性, PSO-KELM取得了平均81.25%的分类正确率, 80.38%的ROC曲线下面积, 82.85%的灵敏性和81.58%的特异性。此外, 观察到算法在每次交叉验证中可以自适应指定参数 $k 和 m$ 的值, 该事实原因在于, 这两个参数可以由粒子群算法根据训练数据的特定分布自适应地决定。

为了分析PSO-KELM算法的收敛性, 本文记录了每一次迭代过程中, 分别在最佳适应度、局部最佳适应度和平均适应度下的分类准确率。图2分别显示了在10折交叉验证中, 第1、3、5、7折交叉验证下PSO-KELM算法的学习曲线。可以看出, 图2(d)中的Best fitness曲线在小于30次迭代后始终收敛到全局最优, 在第1~30次迭代过程中, 它们逐步提高, 在小于30次的某一次迭代后, 不再有显著的提高, 最终在第100次迭代, 即粒子达到停止标准(最大迭代次数)时终止。在演化初始阶段, 分类正确率适应度增长迅速; 在经过一定数量的迭代后缓慢增长; 在演化的后期, 适应度趋于稳定, 直到停止标准满足。这种现象表明, PSO-KELM算法能快速、有效地得到全局最优解。

	Figure Option View Download New Window
	图2 在训练阶段第1、3、5、7折交叉验证的学习曲线Fig.2 Learning curves during training stage for folds 1, 3, 5 and 7 in 10-fold CV

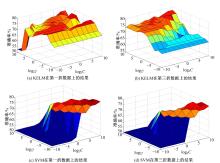为了验证本文方法的有效性, 将其与两种高效的机器学习算法Grid-KELM和SVM进行比较。一种网格搜索技术用于获取Grid-KELM和SVM中RBF核函数的最优参数值, RBF核函数中的相关参数C和 $γ$ 的范围设置为: $C = {2^{- 10}, 2^{- 8}, \dots, 2^{10}}, γ = {2^{- 10}, 2^{- 8}, \dots, 2^{10}},$ 采用最优参数对 $(C, γ)$ 构建预测模型。图3显示了SVM和KELM通过网格搜索策略达到的n折交叉验证的训练分类准确率平面图, 其中x轴和y轴分别是log₂C和log₂γ , 训练准确率(x, y)平面上的每个网格结点表示一个参数组合, $y$ 轴为每个参数组合获得的训练准确率值。

	Figure Option View Download New Window
	图3 通过网格搜索获得参数的KELM和SVM训练准确率曲面图Fig.3 Training accuracy surfaces of Grid-KELM and SVM with parameters obtained by grid search for several folds

Grid-KELM模型获得的平均分类准确率、ROC曲线下面积、灵敏度和特异性分别为79.56%、79.49%、76.02%和82.96%; SVM模型获得的平均分类准确率、ROC曲线下面积、灵敏度和特异性分别为78.36%、78.31%、74.89%和81.71%。如图4所示, 可以看到, PSO-KELM模型在分类准确率、ROC曲线下面积和灵敏度上超过SVM和Grid-KELM, PSO-KELM的特异性也与其他两种方法相近, 该方法的优异性能可能是由于PSO辅助KELM分类器自动检测最优参数对从而达到最高分类性能。

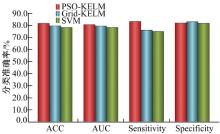	Figure Option View Download New Window
	图4 不同方法在ACC, AUC, sensitivity和specificity方面的分类性能比较Fig.4 Classification performance obtained by different algorithms in terms of ACC, AUC, sensitivity, and specificity

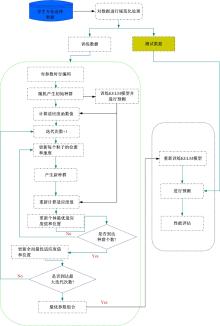
3种方法的标准差如图5所示, 从图5可以看出:在4个评价指标上PSO-KELM的标准差比其他两种方法小得多; PSO-KELM在分类准确率、ROC曲线下面积和特异性方面胜过SVM, 并在灵敏度上比SVM获得略高的标准差值。比较结果显示:PSO-KELM在第二专业选择方面是最稳定和鲁棒的方法, Grid-KELM和SVM方法次之。

	Figure Option View Download New Window
	图5 不同方法在ACC, AUC, sensitivity和specificity方面的标准差比较Fig.5 Standard deviation obtained by different methods in terms of AGG, AUC, Sensitivity, and specificity

4 结束语

探讨了应用KELM分类器辅助学生进行专业选择的可行性, 利用粒子群算法来搜索最优参数, 达到KELM模型的最高性能。实验结果表明, 在真实的数据集上, 开发的模型与其他两种先进的机器学习模型相比, 在分类准确率、ROC曲线下面积、灵敏度和特异性方面具有更好的性能。这表明本文开发的智能系统为学生第二专业选择提供了一种有前景的决策支持系统。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Kardan A A, Sadeghi H, Ghidary S S, et al. Prediction of student course selection in online higher education institutes using neural network[J]. Computers and Education, 2013, 65: 1-11. [本文引用:1]
[2]	Guo W W. Incorporating statistical and neural network approaches for student course satisfaction analysis and prediction[J]. Expert Systems with Applications, 2010, 37(4): 3358-3365. [本文引用:1]
[3]	Campagni R, Merlini D, Sprugnoli R, et al. Data mining models for student careers[J]. Expert Systems with Applications, 2015, 42(13): 5508-5521. [本文引用:1]
[4]	Huang C, Xu J. Second major selection system based on data mining[J]. Journal of Information and Computational Science, 2009, 6(6): 2333-2340. [本文引用:1]
[5]	Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1-3): 489-501. [本文引用:1]
[6]	Huang G B, Zhou H, Ding X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics, 2012, 42(2): 513-529. [本文引用:1]
[7]	Liu B, Tang L W, Wang J B, et al. 2-D defect profile reconstruction from ultrasonic guided wave signals based on QGA-kernelized ELM[J]. Neurocomputing, 2014, 128: 217-223. [本文引用:1]
[8]	Chen H L, Wang G, Ma C, et al. An efficient hybrid kernel extreme learning machine approach for early diagnosis of Parkinson's disease[J]. Neurocomputing, 2016, 184(C) : 131-144. [本文引用:1]
[9]	Liu T, Hu L, Ma C, et al. A fast approach for detection of erythemato-squamous diseases based on extreme learning machine with maximum relevance minimum redundancy feature selection[J]. International Journal of Systems Science, 2015, 46(5): 919-931. [本文引用:1]
[10]	Chen H L, Yang B, Wang S J, et al. Towards an optimal support vector machine classifier using a parallel particle swarm optimization strategy[J]. Applied Mathematics and Computation, 2014, 239: 180-197. [本文引用:1]
[11]	代琨, 于宏毅, 仇文博, 等. 基于SVM的网络数据无监督特征选择算法[J]. 吉林大学学报: 工学版, 2015, 45(2): 576-582. Dai Kun, Yu Hong-yi, Qiu Wen-bo, et al. Unsupervised feature selection algorithm based on support vector machine for network data[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(2): 576-582. [本文引用:1]
[12]	赵东, 臧雪柏, 赵宏伟. 基于果蝇优化的随机森林预测方法[J]. 吉林大学学报: 工学版, 2017, 47(2): 609-614. Zhao Dong, Zang Xue-bai, Zhao Hong-wei. Rand om forest prediction method based on Optimization of fruit fly[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(2): 609-614. [本文引用:1]
[13]	Duan L, Dong S, Cui S, et al. Extreme learning machine with gaussian kernel based relevance feedback scheme for image retrieval[J]. Springer International Publishing, 2016, 1: 397-408. [本文引用:1]
[14]	Chang C C, Lin C J. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 1-27. [本文引用:1]

2013

0.0

... Kardan等^[1]探讨了在网络学习背景下通过数据挖掘技术来预测学生课程选择的情况 ...

2010

0.0

... Guo^[2]提出用统计分析和神经网络建立动态模型来分析和预测学生的课程满意度 ...

2015

0.0

... Campagni等^[3]提出了一种基于聚类和序列模式的高校毕业生职业生涯分析方法,有助于研究生职业生涯规划 ...

2009

0.0

... Huang等^[4]分析了统计学、心理学等评价理论,提出了基于粗糙集的关联规则挖掘算法来进行第二专业选择 ...

2006

0.0

... 核极限学习机是在极限学习机(Extreme learning machine,ELM)^[5,6]基础上发展而来的,是一种新的单隐层的前馈神经网络的学习算法 ...

2012

0.0

... 核极限学习机是在极限学习机(Extreme learning machine,ELM)^[5,6]基础上发展而来的,是一种新的单隐层的前馈神经网络的学习算法 ...

2014

0.0

... 一些研究^[7,8,9]表明,KELM中的一些参数(如惩罚参数 C和核宽度γ)对模型的性能具有显著的影响,因此,本文提出一种群智能技术用于解决KELM模型的参数优化问题,类似于支持向量机(Support vector machines,SVM)^[10,11]和随机森林(Random forest)^[12]的参数优化方法 ...

2016

0.0

2015

0.0

2014

0.0

2015

0.0

. 2015, 45(2):576-582 DOI:doi:10.13229/j.cnki.jdxbgxb201502035

Unsupervised feature selection algorithm based on support vector machine for network data

基于SVM的网络数据无监督特征选择算法

Dai Kun , Yu Hong-yi , Qiu Wen-bo

代琨, 于宏毅, 仇文博

摘　要：面向线性不可分的未知格式网络数据,提出了一种基于支持向量机的无监督特征选择算法。该算法通过非线性映射函数将不可分的网络数据映射到高维空间中,然后在高维空间中进行无监督的特征选择。该算法在特征选择之前不需要人工构造候选特征集合,直接从原始网络数据中自动地选择关键特征。利用人工数据集和网络数据集进行的实验结果表明：本文算法在特征选择可行性和有效性方面都有良好的表现。