分布式测试系统同步触发脉冲传输时延的高精度测量方法

引用本文

牟宗磊, 宋萍, 翟亚宇, 陈晓笑. 分布式测试系统同步触发脉冲传输时延的高精度测量方法[J].吉林大学学报（工学版）, 2018,48(4): 1274-1281
MOU Zong-lei, SONG Ping, ZHAI Ya-yu, CHEN Xiao-xiao. High accuracy measurement method for synchronous triggering pulse transmission delay in distributed test system[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 1274-1281 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170572
Permissions

分布式测试系统同步触发脉冲传输时延的高精度测量方法

牟宗磊, 宋萍, 翟亚宇, 陈晓笑

北京理工大学仿生机器人与系统教育部重点实验室,北京 100081

通讯作者:宋萍(1972-),女,教授,博士生导师.研究方向:传感与测试技术.E-mail:sping2002@bit.edu.cn

作者简介:牟宗磊(1985-),男,博士研究生.研究方向:传感与测试技术.E-mail:mzl127127@bit.edu.cn

基金:国防基础科研重大项目(JCKY2016208B008,JCKY2016209A003).

摘要

针对分布式测试系统中数据采集装置接收到触发指令的时延不同且未知而影响同步触发的问题,提出了一种实时在线测量触发脉冲传输时延测量模型和数据回传模型,以及基于延时链循环比较法的高精度时间间隔测量方法,实现了同步触发脉冲传输时延的精确测量,为后续同步触发误差的精确校准提供了高精度的时延数据。测试结果表明,该方法能实现分布式测试系统同步触发脉冲传输时延的高精度测量。

关键词: 通信技术; 分布式测试; 同步触发; 时延测量模型; 时间间隔测量

中图分类号:TN91 文献标志码:A 文章编号:1671-5497(2018)04-1274-08

High accuracy measurement method for synchronous triggering pulse transmission delay in distributed test system

MOU Zong-lei, SONG Ping, ZHAI Ya-yu, CHEN Xiao-xiao

Key Laboratory of Biomimetic Robots and System,Beijing Institute of Technology,Beijing 100081,China

Abstract

A real-time triggering transmission delay measurement model and a data transfer model are proposed to solve the problem that the delay time of triggering instruction received by the data acquisition node in distributed test system is different and unknown. Furthermore, a high-precision time interval measurement method with the use of delay chain cycle comparison is proposed to achieve the propagation delay of the synchronous triggering pulse. The delay measurement provides high-precision delay data for subsequent calibration of the synchronization triggering error. The test results show that the proposed method can realize high-precision measurement of the synchronous triggering pulse transmission delay in distributed test system.

Keyword: communication technology; distributed testing; synchronous trigger; delay measurement model; time interval measurement

文章图片

0 引言

大规模数据采集系统主要被设计成多节点分布式结构来完成数据的采集和分析。分布式测试系统中多个数据采集装置的同步触发精度直接关系到数据采集的有效性以及后续数据分析的准确性^{[1, 2]}。因此, 研究分布式测试系统的同步触发技术具有重要意义。当前, 几种常用的同步触发技术, 如基于全球定位系统(GPS)的同步触发, 基于断线及无线电台的同步触发, 这些触发方式的信号传输时延具有随机不确定性, 同步触发精度对于一般低采样率的分布式测试系统来说是可以接受的, 但是无法满足一些具有高采样率需求的瞬态类信号的分布式测试系统^[3]。另外, 基于GPS及无线电台的无线同步触发方式对于复杂环境的环境适应性不是很好。

通常, 不同布设位置处的数据采集装置, 各个数据采集装置上的工作时钟是互不相关的, 而且触发指令到达各个数据采集装置的时延不同, 因此非同步触发的问题出现了。准确的试验数据分析和信号的时空场传播规律要求所有测试装置必须高精度同步触发, 因此对触发脉冲传输时延的精确测量提出了要求^[4]。

基于以上问题, 本文重点研究了复杂环境下基于分布式光纤测试系统的多数据采集装置的同步触发问题, 提出了一种分布式测试系统同步触发脉冲传输时延的测量模型和数据回传模型, 采用延时链循环比较时延测量算法精确计算触发信号到达各个数据采集装置的时延值, 为后期的同步触发提供准确的时延校正值, 实现各个数据采集装置的高精度同步触发。最后, 在搭建的试验验证环境中进行了同步触发脉冲传输时延高精度时间间隔测量功能的验证。

1 有线分布式测试系统架构

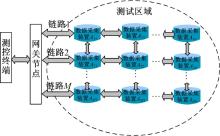
本文所设计的试验测试系统是以复杂电磁干扰环境下的测试为背景, 以瞬态类信号采集为试验对象。综合考虑瞬态类信号的时效性和测试系统的实际布设情况, 本系统采用基于分布式光纤技术的有线测试, 解决常规无线测试系统以及基于GPS的分布式测控系统同步触发技术不能适应复杂环境的问题。有线分布式测试系统架构如图1所示, 主要有上位机测控终端平台、网关节点以及布设在测试区域内基于现场可编程门阵列(Field-programmable gate array, FPGA)的数据采集装置构成。测试区域中基于光纤串联的各个数据采集装置相互独立, 主要用于各种瞬态信号的采集。网关节点主要完成以下功能:①采用高精度时间间隔测量模块完成触发指令到达各个数据采集装置传输时延的精确测量和计算; ②完成对测控终端各种命令的解析和下发以及将测试系统内各个数据采集装置的工作状态和采样数据预处理后上传到测控终端。光纤主要用于网关节点与数据采集装置之间各种控制指令的传输以及采集数据的有效回传, 解决复杂环境下分布式数据采集装置的高精度同步触发问题、抗电磁干扰能力问题以及数据传输有效性问题^{[5, 6]}。

	Figure Option View Download New Window
	图1 有线分布式测试系统架构Fig.1 Architecture of wired distributed test system

2 高精度时延测量技术

在大规模分布式测试系统中, 网关节点上的全局主时钟精度以及测试系统控制命令的传输时延是导致同步触发误差的主要原因。建立时延测量模型后, 更进一步的工作是完成对触发指令传输时延的精确估计与测量。精确测量触发信号到达各个数据采集装置的时延值后, 通过一定的时延补偿算法可以实现数据采集装置的高精度同步触发^[7]。在分布式测试系统中, 各个数据采集装置的布设位置与节点之间的链路链接距离在满足不同的测试环境和测试需求下灵活配置, 传输距离的差异导致信号的传输时延不同, 实时在线测量触发指令到达各个测试节点的传输时延对分布式测试系统的高精度同步触发至关重要。触发指令可以有多种形式, 如命令字节的形式或者脉冲的形式。鉴于网关节点发送数据指令到各数据采集装置需要一定的时延, 各节点接收到命令字节按既定通信协议进行解析也需要一定的时延, 而且每次解析指令的时间具有随机不确定性。相比之下, 触发脉冲以光速传播, 省去了指令解析的不确定时间因素, 可以实现多数据采集装置“ 即时” 响应触发指令。因此, 本文设计的分布式测试系统采用脉冲的形式进行触发, 采用高精度时间间隔测量方法实现触发脉冲传输时延的精确测量。

2.1 触发脉冲传输时延的精确测量

本系统采用了一种基于延时链循环比较法实时在线测量触发脉冲传输时延的方法。

2.1.1 测量原理

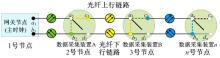
时延测量模型如图2所示, 网关节点与数据采集装置之间通过分布式光纤和硬件搭载的光纤收发一体模块进行通信。网关节点发出触发脉冲的同时启动自身的高精度计数器, 触发脉冲沿 $a_{1} \to a_{2}$ 链路从网关节点传送到数据采集装置A上, 脉冲信号一路用于触发数据采集装置A; 另一路借助数据采集装置A上的组合逻辑电路沿光纤链路 $a_{2} \to b_{2} \to b_{1}$ 回传到网关节点进行时延测量。当网关节点上的高精度计数器检测到A回传的触发脉冲时, 停止计数并保存当前计数器内的计数值Count1。同理, 触发脉冲沿 $a_{1} \to a_{2} \to c_{2} \to a_{3}$ 传送到数据采集装置B上, 然后沿 $b_{3} \to d_{2} \to b_{2} \to b_{1}$ 回传到网关节点, 网关节点保存当前的计数值Count2。以此类推, 当网关节点检测到第 $n 个数据采集装置沿 b_{n} \to d_{3} \to b_{3} \to d_{2} \to b_{2} \to b_{1}$ 回传的触发脉冲时, 保存当前计数器的值Countn, 时延测量完成^[4]。

	Figure Option View Download New Window
	图2 时延测量模型Fig.2 Delay measurement model

网关节点通过高精度时间间隔测量技术依次测量主节点(网关节点)与从节点(数据采集装置)之间触发脉冲的传输时延。传统的时延测量方法需要主、从节点之间进行多次时间信息的交换, 而且测量误差与主、从节点间的时钟精度密切相关, 测量过程相对复杂, 测量精度相对较低。本文方法的最大优势是所测时间间隔精度主要与主节点的时钟精度相关, 简化了时延测量算法的测量过程, 并提高了算法的精度。

传输时延是由网关节点上的高精度时间间隔测量模块对同步触发脉冲测量所得, 是同步触发脉冲在整个传输链路上的时间间隔测量值, 包括网关节点和数据采集装置上的光电转换以及电光转换的时延, 光纤收发一体模块的发送与接收时延以及光纤链路的传输时延。基于FPGA实现的高精度时间间隔测量方法, 当环境温度和供电电压变化时会引起FPGA内部逻辑门传输时延的变化, 进而影响延时链整体时延的变化, 影响时间间隔测量的精度和稳定性, 造成线路传输的时间不确定性。另外, 本文所研究的分布式测试系统是基于单纤双向光纤实现的, 测试系统采用不同波长光信号往返传输, 不同波长的光纤色散将引入一部分时间传递误差, 也会造成线路传输的时间不确定性。

假设主节点发送触发脉冲信号到从节点接收到触发脉冲信号的时间间隔为:

$τ_{ms} = t_{sr 1} - t_{ms 1} = S_{m} + T_{ms} (λ_{1}) + R_{s}$ (1)

从节点接收到触发脉冲信号回传到主节点的时间间隔为:

$τ_{sm} = t_{mr 2} - t_{ss 2} = S_{s} + T_{sm} (λ_{2}) + R_{m}$ (2)

式中: $t_{ms 1}$ 是网关节点相对于本地时钟的发送时刻; $t_{ss 2}$ 是从节点相对于本地时钟的发送时刻; $t_{mr 2}$ 是网关节点相对于本地时钟接收到触发脉冲信号的时刻; $t_{sr 1}$ 是从节点相对本地时钟接收到触发脉冲信号的时刻; $S_{i} (i$ =m、s)是光纤收发一体模块的发送时延; $R_{i} (i$ =m、s)是光纤收发一体模块的接收时延; $T_{ms} (λ_{1})$ 是网关节点到从节点的光纤链路传输时延; $T_{sm} (λ_{2})$ 是从节点到网关节点的光纤链路传输时延, 其中λ ₁=1310 nm, λ ₂=1550 nm。

网关节点和数据采集装置上的光纤收发一体模块结构一致, 采用的FPGA芯片一致, 采用单纤双向光纤进行链接, 链路高度对称, 往返链路双向时延随温度的变化近似相等, 在不考虑光纤色散对链路传输时延的影响下, 可以假定 $S_{m} = S_{s} = S_{t} 、 R_{m} = R_{s} = R_{t} 。$ 光纤链路传输时延值计算公式为:

$\begin{array}{l} T_{av} = [T_{ms} (λ_{1}) + T_{sm} (λ_{2})] / 2 = \\ (t_{sr 1} - t_{ms 1} + t_{mr 2} - t_{ss 2} - 2 S_{t} - 2 R_{t}) / 2 \end{array}$ (3)

网关节点发送触发脉冲到数据采集装置回传触发脉冲到网关节点的时间间隔 $Δ t$ 为:

$\begin{array}{l} Δ t = (τ_{ms} + τ_{sm}) / 2 = \\ (S_{m} + T_{ms} (λ_{1}) + R_{s} + S_{s} + T_{sm} (λ_{2}) + R_{m}) / 2 \end{array}$ (4)

在这里各数据采集装置接收到触发脉冲时, 立即回传给网关节点, FPGA的并行时序性很强, 可认为 $t_{sr 1} = t_{ss 2},$ 则式(4)可以简化为:

$Δ t = (τ_{ms} + τ_{sm}) / 2 = (t_{mr 2} - t_{ms 1}) / 2$ (5)

从式(5)可以看出, 触发脉冲的时延与主节点时钟的精度密切相关, 触发脉冲时延测量转换为高精度时间间隔的测量。

在时延测量模型和数据回传模型建成后, 网关节点依次对各个数据采集装置进行触发脉冲的时间间隔测量。测试完成后通过光纤收发一体模块把时间间隔测量值依次传递到各个数据采集装置, 数据采集装置根据时延测量算法所得的时延值, 采用电学补偿方式补偿触发脉冲的传输时延, 进而实现各数据采集装置的高精度同步触发。因此, 网关节点上的高精度时间间隔测量模块是实现整个测试系统高精度同步触发的关键。

3 高精度时间间隔测量技术

高精度时间间隔测量分为整数倍周期内的时间间隔测量和小数周期内的时间间隔测量。其中触发脉冲与网关节点时钟(主时钟)之间的小数周期内的时间间隔测量是本文研究的重点。结合时钟计数法的使用可以实现大范围、高精度的时间间隔测量。常用的基于参考时钟计数器时间间隔测量方法中, 被测时间间隔的开始脉冲信号和结束脉冲信号与本地时钟的相位是不相关的, 存在一定的随机性和相位抖动问题。由于被测触发脉冲时间间隔的上升沿与本地参考时钟的上升沿之间存在相位偏差, 导致所测时间间隔存在± 1个参考时钟周期误差。虽然高分辨的参考时钟可以提高时延测量的精度, 例如采用1 GHz的晶振, 参考时钟的周期误差可以缩减到1 ns, 但对板级电路的要求比较严, 成本较高, 不适用于大范围的分布式测试系统。本文采用延时链循环比较时间间隔测量法, 在低成本、低速率板级晶振的FPGA上实现高精度的时间间隔测量。

3.1 测量原理

基于延时链循环比较法进行时间间隔测量的原理如图3所示, 参考时钟计数器用于测量整数倍的参考时钟周期内的时间间隔, 延时链循环比较法用于测量小数参考时钟周期内的时间间隔, 二者测量之和即为两个触发脉冲之间的被测时间间隔^[8]。同时, 基于延时链循环比较法的时间间隔测量法基于延时链的整体时延考虑, 消除了单个逻辑门延时较大、不一致的影响。两个延时链由相同结构的延时逻辑门组成, 通过时序约束, 保证了“ 开始” 延时链的整体时延大于“ 结束” 延时链的整体时延。

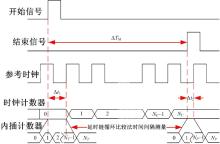	Figure Option View Download New Window
	图3 基于延时链循环比较法时间间隔测量的原理图Fig.3 Principle map of time interval measurement based on loop comparison method in delay chain

被测触发脉冲之间的时间间隔 $Δ T_{M}$ 的计算公式为:

$\begin{array}{l} Δ T_{M} = N_{C} + Δ t_{1} - Δ t_{2} = \\ Count_i \times T_{CLK} + Δ t_{1} - Δ t_{2} \\ i = 1, 2, \dots, n \end{array}$ (6)

式中: $N_{C}$ 为参考时钟计数器测得的整数周期部分的时间间隔; $Count_i$ 为时钟计数器的计数值; $T_{CLK}$ 为计数器的参考时钟周期; $Δ t_{1} - Δ t_{2}$ 为采用延时链循环比较原理测得的小数周期部分的时间间隔。

3.2 延时链循环比较法的整体设计

基于延时链循环比较法的时间间隔测量的整体结构框图如图4所示, 主要有开始信号和结束信号的窄脉冲生成器、多路选择器、延时链路1、延时链路2、相位一致性检测器以及循环次数计数模块等组成。

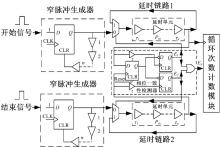	Figure Option View Download New Window
	图4 基于延时链循环比较法时间间隔测量的整体结构框图Fig.4 Overall structure of time interval measurement based on loop comparison method in delay chain

窄脉冲生成器将开始、结束触发脉冲整形为具有一定脉冲宽度的循环脉冲信号, 经过多路选择器选择后分别在延时链路1和延时链路2中传输, 每循环一次出延时链时被测时间间隔缩短一个分辨率, 循环次数计数器加1, 相位一致性检测器对出链后的开始循环脉冲和结束循环脉冲的相位进行实时检测。经过几个周期延时链的循环比较, 当相位一致性检测器检测到该时刻的时间间隔小于延时链的测量分辨率时, 两个延时链同时断开, 时间间隔测量完成, 循环次数计数器停止计数并锁存当前的计数值, 所测时间间隔的小数部分为延时链的测量分辨率与循环次数的乘积。

3.2.1 延时链路的具体设计

如图4所示, 本文设计的延时链环路有27个BUFF缓冲器延时单元 $τ_{i} 、$ 一个多路选择器和脉冲再生电路 $p_{re}$ 组成, 延时链环路的整体时延的计算公式为:

$T_{loop} = 27 T_{buff} + T_{MX 2} + T_{pulse}$ (7)

式中: $T_{buff}$ 是缓冲器BUFF的传输时延; $T_{MX 2}$ 是多路选择器的传输时延; $T_{pulse}$ 是脉冲再生成触发器的传输时延, FPGA内部单个逻辑门的时延为400 ps左右, 这3种逻辑单元的传输时延不同但都可以通过搭载延时链电路加高质量的数字示波器测得, 因此整个延时链的传输时延可以测得。FPGA内部由缓存器BUFF组成的延时链中, 单个脉冲信号循环传输几次后波形可能会失真影响相位一致性检测, 因此在每个延时链中加了一个脉冲再生成电路 ${p_{re}}^{[9]}$ , 脉冲再生成电路的结构与窄脉冲生成器的结构相同。

3.2.2 相位一致性检测器

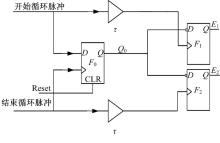
如图5所示, 相位一致性检测器主要有延时缓冲器BUFF和触发器FF组合而成。开始循环脉冲和结束循环脉冲分别经过一个缓冲器BUFF延时后连接到触发器F₀的数据段和时钟段, Reset复位键连接到触发器F₀的CLR端。

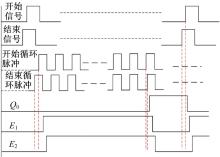
	Figure Option View Download New Window
	图5 相位一致性检测器原理图Fig.5 Principle map of phase consistency detector

高精度时间间隔开始测量时, 开始信号和结束信号经过窄脉冲生成器和多路选择器后分别输送到延时链路1和延时链路2中。测量初期阶段, 开始循环脉冲信号的上升沿超前于结束循环脉冲信号的上升沿, 由F₀的工作特性可知, 相位一致性检测器的Q₀端输出为0, F₁、F₂的输出端都为1, 即多路选择器的使能端E₁、E₂都为1, 延时链路1和延时链路2都闭合。经过一段时间的循环比较, 当开始循环脉冲信号的上升沿滞后于结束循环脉冲的上升沿时, Q₀端输出变为1, F₁、F₂的输出端都为0, 即E₁、E₂都为0, 则延时链1和延时链路2都断开, 循环比较结束, 循环次数计数器锁存当前的计数值并准备下次时间间隔测量。相位一致性检测器的具体工作时序如图6所示。

	Figure Option View Download New Window
	图6 相位一致性检测器的时序图Fig.6 Timing diagram of phase consistency detector

3.3 延时链循环比较法的具体实现

基于延时链循环比较法实现的高精度时间间隔测量的时序图如图7所示, 其中被测时间间隔的触发脉冲信号和结束脉冲信号被作为时间间隔测量的开始信号, 并产生窄脉冲信号, 参考时钟作为时间间隔测量的结束信号。

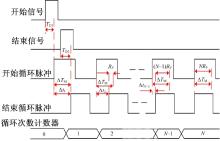$T_{D 1}$ 是由开始信号启动窄脉冲电路产生开始循环脉冲时产生的固定时延; $T_{D 2}$ 是由结束信号启动窄脉冲电路产生结束循环脉冲时产生的固定时延。开始、结束循环脉冲分别在开始延时链和结束延时链中循环, 每循环一周由相位一致性检测器检测两者的相位变化, 当检测到两者的相位一致时, 断开延时链停止脉冲循环。脉冲每循环一周时间间隔缩减一个分辨率 $R_{F}, N$ 次循环以后, 测量完毕, 被测时间间隔的小数部分等于 $N$ 倍的R_F。对网关节点发出的触发脉冲信号和接收到的触发脉冲信号都进行高精度时间间隔测量, 结合整数倍时钟计数器的值可以得到触发脉冲在整个传输链路的时延值。

	Figure Option View Download New Window
	图7 基于延时链循环比较法时间间隔测量的时序图Fig.7 Timing diagram of time interval measurement based on loop comparison method in delay chain

理论上根据两个延时链间的链路时延差, 通过多次循环比较, 可以更高程度地提高延时链的测量分辨率, 进而提高时间间隔的测量分辨率, 但是影响延时链测量精度的因素很多, 其中信号抖动、温度变化以及供电电压的变化是影响延时链循环比较法精度的重要因素^[10]。脉冲信号的边缘抖动与时间间隔 $Δ T$ 有关, 二者之间的关系如下:

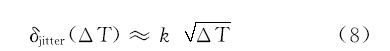
式中: $k$ 是一个与延时链电路相关的系数。

在基于延时链循环比较法的时间间隔测量过程中, 时间间隔开始测量后开始循环脉冲和结束循环脉冲在各自的延时链中循环传输, 测试结束后停止传输复位循环次数计数器, 准备下次测量。式(8)中, $Δ T$ 是高精度时延测量模块测量被测时间间隔 $Δ T_{M}$ 所需的测量时间, 随着 $Δ T_{M}$ 的增大而增大。测量时间 $Δ T$ 与测量分辨率 $R_{F}$ 的计算公式为:

$Δ T = Δ T_{M} / R_{F}$ (9)

其中测量分辨率 $R_{F}$ 的计算公式为:

$R_{F} = T_{start_loop} - T_{stop_loop}$ (10)

式中: $T_{start_loop}$ 为开始脉冲延时链的整体时延; $T_{stop_loop}$ 为结束脉冲延时链的整体时延。

两个延时链中循环脉冲是随机不相关的, 但两者的逻辑结构相同, 可以简化为两者引起的时延抖动基本一致, 则:

在实际的电路测试中发现, 延时链在100 ps级精度时, 时钟随机抖动比较小, 10 ps级精度以下时, 时钟随机抖动严重影响测量精度。综合以上考虑, 本文设计的延时链测量精度为100 ps级, 时钟采用200 MHz高精度恒温晶振驱动。

本文提出的高精度时间间隔测量技术是基于内插法原理实现的, 主要包括时间间隔内插器和时钟计数器。参考时钟计数器用于测量整数周期的时间间隔以满足不同测量范围的要求, 而基于延时逻辑门内插器原理实现的延时链用于测量小数周期内的时间间隔以满足高精度的要求^[11]。本文提出的高精度时间间隔计数器可以在低成本、低速参考时钟的FPGA芯片上借助丰富的片内资源来实现, 降低了实现成本和电路设计复杂度。

4 试验验证及数据分析

为了验证整个时延测量电路精确度和系统稳定性, 并使验证试验尽量与真实情况一致, 在线性网络拓扑结构上的数据采集装置与网关节点之间进行了时延测量, 随机选择一条链路上的3个数据采集装置作为测试节点。时延测量示意图如图8所示, 其中网关节点作为1号节点, 离网关最近的数据采集装置作为2号节点, 后面依次为3号节点和4号节点, 节点之间采用相同长度的光纤(5 m)进行连接。

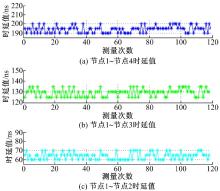
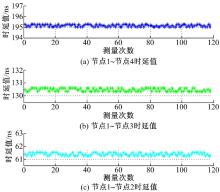
	Figure Option View Download New Window
	图8 试验验证平台Fig.8 Experimental verification platform

为进一步验证本文时延测量方法的稳定性和精度, 进行了120组时延测量试验, 一组为采用参考时钟计数法测得的时延值, 如图9所示; 另一组为对应情况下采用高精度时间间隔测量方法测得的时延值, 如图10所示。

	Figure Option View Download New Window
	图9 采用参考时钟计数法所测时延值Fig.9 Measured delay values based on reference clock counting method

从图9和图10可以看出, 时延测试方法是一个符合统计规律的测试过程, 为进一步研究时延测量方法的误差分布情况, 对120组时延的测试结果进一步分析得到两种方法测量结果的期望和均方差如表1、表2所示。

	Figure Option View Download New Window
	图10 采用延时链循环比较法所测时延值Fig.10 Measured delay values based on loop comparison method in delay chain

从以上分析可知, 采用参考时钟计数法对触发脉冲传输时延值进行测量时, 由于触发脉冲与时钟信号的随机不相关性, 导致所测时延值存在± 1个参考时钟周期的计数误差, 网关节点采用200 MHz晶振驱动计数器时, 根据式(5)计算的时延值存在± 5 ns的计数误差, 而根据延时链循环比较法的时间间隔测量可以准确获得触发信号与时钟的相位关系, 根据式(6)可以精确测量同步触发脉冲的时延值, 测量精度为百ps级。时延值具有随光纤链路节点之间距离的增加而增长的趋势, 测量误差没有随着数据采集装置数量的增加而呈现发散趋势, 而是稳定分布在某些值附近, 试验验证了本文时延测量模型以及数据回传模型的有效性, 本文时延测量方法具有较高的测量稳定性和精度等级。

表1 采用参考时钟计数法所测时延值的期望和均方差 Table 1 Expectation and unbiased variance of time delay based on reference clock counting method

表2 采用延时链循环比较法所测时延值的期望和均方差 Table 2 Expectation and unbiased variance of time delay based on loop comparison method in delay chain

5 结束语

本文以复杂环境下瞬态类信号的数据采集需求为背景, 设计了基于分布式光纤通信技术的分布式测试系统, 重点研究了复杂环境下分布式测试系统的高精度同步触发问题。提出了一种实时在线测量触发脉冲传输时延测量和数据回传模型, 在有限的系统硬件资源上, 提出了一种基于延时链循环比较法的高精度时间间隔测量技术来实现同步触发脉冲传输时延的精确测量。在系统初始化阶段或者正式采集数据前, 利用链路之间的光纤实现主从节点间同步触发脉冲传输时延的精确测量, 进而实现复杂环境下分布式测试系统的高精度同步触发。试验系统验证了本文时延测量模型和数据回传模型以及高精度时延测量方法的正确性及有效性, 在不需要格外增加时间同步芯片的情况下, 基于延时链循环比较法的高精度时间间隔测量技术在低成本FPGA上实现了高精度同步触发, 对工程实际应用具有重要意义。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	游雪峰, 文玉梅, 李平. 以太网分布式数据采集同步和实时传输研究[J]. 仪器仪表学报, 2006, 27(4): 384-388. You Xue-feng, Wen Yu-mei, Li Ping. Study on the synchronization of distributed data acquisition and real-time transmission based on Ethernet[J]. Chinese Journal of Scientific Instrument, 2006, 27(4): 384-388. [本文引用:1]
[2]	闵卫东, 石杰, 韩清, 等. 一种分布式人脸识别方法及性能优化[J]. 光学精密工程, 2017, 25(3): 779-785. Min Wei-dong, Shi Jie, Han Qing, et al. A distributed face recognition method and performance optimization[J]. Optics and Precision Engineering, 2017, 25(3): 779-785. [本文引用:1]
[3]	Song K Z, Cao G P, Yang J F, et al. A high-precision synchronous sampling approach for large-scale distributed wire sensor networks in seismic data acquisition systems[J]. Instrumentation Science & Technology, 2012, 40(6): 567-579. [本文引用:1]
[4]	Jiang J, Duan F, Chen J, et al. Calibration method of the time synchronization error of many data acquisition nodes in the chained system[J]. Journal of Geophysics and Engineering, 2012, 9(4): 413-422. [本文引用:2]
[5]	黄璜, 吴龟灵, 胡亮, 等. 温度对双向时分复用光纤时间传递精度的影响[J]. 光学学报, 2015(5): 97-103. Huang Huang, Wu Gui-ling, Hu Liang, et al. Influence of temperature on the precision of bidirectional TDM based fiber-optic time transfer[J]. Acta Optica Sinica, 2015(5): 97-103. [本文引用:1]
[6]	董杰. 空间差分干涉的光纤分布式水下声波测量[J]. 光学精密工程, 2017, 25(9): 2317-2323. Dong Jie. Measurement of underwater acoustic wave using optical distributed acoustic sensing based on space difference[J]. Optics and Precision Engineering, 2017, 25(9): 2317-2323. [本文引用:1]
[7]	蒋佳佳, 段发阶, 陈劲, 等. 链式系统中信号远距离传输延时的在线测量方法[J]. 吉林大学学报: 工学版, 2013, 43(2): 520-525. Jiang Jia-jia, Duan Fa-jie, Chen Jin, et al. Real-time online measurement of the transmission time delay in long-distance chained systems[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(2): 520-525. [本文引用:1]
[8]	宋建辉, 袁峰, 丁振良. 脉冲激光测距中高精度时间间隔的测量[J]. 光学精密工程, 2009, 17(5): 1047-1050. Song Jian-hui, Yuan Feng, Ding Zhen-liang. High precision time interval measurement in pulsed laser ranging[J]. Optics and Precision Engineering, 2009, 17(5): 1047-1050. [本文引用:1]
[9]	Andersson N U, Vesterbacka M. A Vernier time-to-digital converter with delay latch chain architecture[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2014, 61(10): 773-777. [本文引用:1]
[10]	杜保强, 周渭. 基于延时复用技术的短时间间隔测量方法[J]. 天津大学学报, 2010(1): 77-83. Du Bao-qiang, Zhou Wei. Short time interval measurement method based on delay-time multiplexing technique[J]. Journal of Tianjin University, 2010(1): 77-83. [本文引用:1]
[11]	Wang H, Zhang M, Liu J. High-resolution short time interval measurement system implemented in a single FPGA chip[J]. Chinese Science Bulletin, 2011, 56(12): 1285-1290. [本文引用:1]

2006

0.0

. 2006, 27(4):384-388 DOI:doi:10.3321/j.issn:0254-3087.2006.04.013

Study on the synchronization of distributed data acquisition and real-time transmission based on Ethernet

以太网分布式数据采集同步和实时传输研究

You Xue-feng , Wen Yu-mei , Li Ping

游雪峰, 文玉梅, 李平

研究虚拟仪器通过以太网控制分布式数据采集嵌入式系统进行同步数据采集和实时数据传输.通过分析各采集单元的采集同步误差源,提出减小同步误差的方法;分析通用嵌入式数据采集系统同时实现数据采集和实时传输的难点,提出解决方案.在各采集系统中运用以太网、TCP/IP网络通信协议,通过对标准网络协议进行改进、简化,减小网络延时,提高系统网络速度和实时性.对系统的网络速度、可靠性、同步误差以及实时性的实验测试,验证了系统方案的可行性和对标准网络协议改进、简化的有效性.

... 分布式测试系统中多个数据采集装置的同步触发精度直接关系到数据采集的有效性以及后续数据分析的准确性^[1,2] ...

2017

0.0

. 2017, 25(3):779-785

A distributed face recognition method and performance optimization

一种分布式人脸识别方法及性能优化

Min Wei-dong , Shi Jie , Han Qing

闵卫东, 石杰, 韩清

... 分布式测试系统中多个数据采集装置的同步触发精度直接关系到数据采集的有效性以及后续数据分析的准确性^[1,2] ...

2012

0.0

... 当前,几种常用的同步触发技术,如基于全球定位系统(GPS)的同步触发,基于断线及无线电台的同步触发,这些触发方式的信号传输时延具有随机不确定性,同步触发精度对于一般低采样率的分布式测试系统来说是可以接受的,但是无法满足一些具有高采样率需求的瞬态类信号的分布式测试系统^[3] ...

2012

0.0

... 准确的试验数据分析和信号的时空场传播规律要求所有测试装置必须高精度同步触发,因此对触发脉冲传输时延的精确测量提出了要求^[4] ...

... 以此类推,当网关节点检测到第 n个数据采集装置沿bn→d3→b3→d2→b2→b1回传的触发脉冲时,保存当前计数器的值Countn,时延测量完成^[4] ...

0.0

. , 2015(5):97-103

Influence of temperature on the precision of bidirectional TDM based fiber-optic time transfer

温度对双向时分复用光纤时间传递精度的影响

Huang Huang , Wu Gui-ling , Hu Liang

黄璜, 吴龟灵, 胡亮

... 光纤主要用于网关节点与数据采集装置之间各种控制指令的传输以及采集数据的有效回传,解决复杂环境下分布式数据采集装置的高精度同步触发问题、抗电磁干扰能力问题以及数据传输有效性问题^[5,6] ...

2017

0.0

. 2017, 25(9):2317-2323

Measurement of underwater acoustic wave using optical distributed acoustic sensing based on space difference

空间差分干涉的光纤分布式水下声波测量

Dong Jie

董杰

为了实现大范围的水下微弱声波探测,提出了一种基于后向瑞利散射空间差分干涉的光纤分布式声波检测(DAS)技术。声波振动引起单模传感光纤中后向瑞利散射光的变化,将含有声波信息的后向瑞利散射光注入到非平衡迈克尔逊干涉仪,调节干涉仪的臂长差实现不同长度的相邻空间段的后向瑞利散射光干涉,然后采用3×3耦合器解调技术解调出相位信息,实现声波信号的测量。实验搭建了一套基于DAS技术的水下声波测量系统,该系统不仅能够实时准确定位两个声波位置,还能还原声波的幅值、频率、相位等信息,并且实现了1kHz情况下的-148.8dB(re rad/μPa)水下声压相位灵敏度,100~1 500Hz频率的频响平坦度在1.2dB之内。实验结果证实DAS技术能够实时快速地实现多个声波信息的定量测量。

2013

0.0

. 2013, 43(2):520-525

Real-time online measurement of the transmission time delay in long-distance chained systems

链式系统中信号远距离传输延时的在线测量方法

Jiang Jia-jia , Duan Fa-jie , Chen Jin

蒋佳佳, 段发阶, 陈劲

A lot of acquisition nodes are arranged in a straight line in seismic streamer, so there is large transmission time delay for the signal from one node to another. Meanwhile, different nodes generate different transmission time delays which are unknown; therefore, the delay time can not be accurately corrected, causing bad result of synchronization accuracy. To solve this problem, a model of "the signal return" and a measuring method of the transmission time delay were proposed. Employing the link multiplexing technology, the transmission time delay from the pre-processing module to all nodes can be measured accurately through the same clock signal line only, and the transmission delay time with each node can be transmitted to the corresponding node. This can provide a precise delay time, which allows the error of delay time to be accurately corrected. Experiment results with three nodes demonstrate the effectiveness of the proposed method.

针对地震勘探系统结构成链式、采集节点多,全局主时钟和系统控制命令在其间传输延时大,而且采集节点间产生的延时不同且未知,导致不同采集通道间同步采集误差不易得到精确校正而影响同步精度的问题,提出了一种实时在线测量信号传输延时的回传模型和方法,采用链路复用技术,用同一根下行链路传输线实现从预处理模块到所有采集节点传输延时的精确测量,并能同时实现延时量向各采集节点一对一地传输。在进行链式系统设计时,本文方法能为后续同步采集误差的精确校正提供精确的延时依据。最后,建立了具有3个采集节点的实验系统,实验结果验证了本文方法的有效性。

... 精确测量触发信号到达各个数据采集装置的时延值后,通过一定的时延补偿算法可以实现数据采集装置的高精度同步触发^[7] ...

2009

0.0

. 2009, 17(5):1047-1050 DOI:doi:10.3321/j.issn:1004-924X.2009.05.017

High precision time interval measurement in pulsed laser ranging

脉冲激光测距中高精度时间间隔的测量

Song Jian-hui , Yuan Feng , Ding Zhen-liang

宋建辉, 袁峰, 丁振良

考虑时间间隔测量对脉冲激光测距系统的意义,提出了一种新的高精度时间间隔测量方法。该方法在现场可编程门阵列(FPGA)中实现了脉冲计数法、多相采样法和延迟链法的结合。采用脉冲计数法对被测时间间隔进行"粗值"测量,保证大的动态测量范围。利用FPGA内部锁相环产生N路同频率,相位均匀分布的时钟信号作为计数时钟,基于等精度测频原理,将被测时间间隔的测时分辨率提高到Tclk/N。利用FlipFlop锁存器形成延时链,对被测信号与相邻计数时钟的时间间隔进一步量化。该方法解决了传统多相采样技术中由于倍频次数高导致相移分辨率降低的问题,在不增加计数时钟和有限延迟链数量的前提下,得到较高测时分辨率。测试结果表明,该时间间隔测量模块的动态测量范围为163.8μs,测时过程相对较短,当进行多次重复测量时,测量的标准误差在71 ps以内,基本满足实际应用的精度要求。

... 1 测量原理基于延时链循环比较法进行时间间隔测量的原理如图3所示,参考时钟计数器用于测量整数倍的参考时钟周期内的时间间隔,延时链循环比较法用于测量小数参考时钟周期内的时间间隔,二者测量之和即为两个触发脉冲之间的被测时间间隔^[8] ...

2014

0.0

2010

0.0

... 理论上根据两个延时链间的链路时延差,通过多次循环比较,可以更高程度地提高延时链的测量分辨率,进而提高时间间隔的测量分辨率,但是影响延时链测量精度的因素很多,其中信号抖动、温度变化以及供电电压的变化是影响延时链循环比较法精度的重要因素^[10] ...

2011

0.0

... 参考时钟计数器用于测量整数周期的时间间隔以满足不同测量范围的要求,而基于延时逻辑门内插器原理实现的延时链用于测量小数周期内的时间间隔以满足高精度的要求^[11] ...