作者简介:姚海洋(1991-), 男, 博士研究生.研究方向:混沌信号处理.E-mail:hyang@mail.nwpu.edu.cn
针对Duffing振子信号检测系统存在的输入噪声对系统扰动的影响、目标信号与内策动力的相位同步以及系统输出运动状态判断3个关键性问题,分别提出了相应的解决方法。提出了一种基于临界阈值字典的逆向相变方法,根据临界阈值随噪声强度的单调性建立临界阈值字典,有效避免了低信噪比下输入噪声对系统的扰动。提出了一种双系统联合检测方法,解决了目标信号相位和内策动力相位不同步问题,并推导出了由于相位的不遍历性导致的虚惊概率。提出了一种基于输出相空间图形表征的系统运动状态判断方法,并进行了可行性的数学证明,实现了检测结果的低运算量、高精度的嵌入式表征。最终建立了适用于工程实际的低信噪比下Duffing振子信号检测模型,使得检测概率不变的前提下最低检测信噪比大幅度降低。
Three efficient methods are proposed to solve three key problems in Duffing oscillator detection system, including the system perturbation by input noise, the synchronization of phase position of driving force and target signal, and the judgment of system output state. First, a reverse phase change method based on the critical threshold dictionary is proposed, where the dictionary is built on the monotonic property of the critical threshold with the change of noise intensity, so that the input signal perturbation is reduced efficiently under low Signal to Noise Ratio (SNR). Second, a double system joint detection method is proposed to solve the problem of phase position synchronization of driving force and target signal. Third, a state of system motion judgment method based on output phase space graph representation is proposed and its feasibility is proved mathematically. The embedded representation of the detection results is fulfilled with low computation and high precision. Finally, the Duffing oscillator detection model suitable to engineering practice is built under low SNR, by which the lowest detection SNR is reduced significantly with constant detection probability.
随着信息技术的需求和发展, 强噪声背景下微弱信号的检测成为国内外学者的研究热点。传统基于统计理论的信号检测方法主要靠抑制噪声, 会对原始信号产生损害, 同时也无法满足检测的低信噪比要求[1, 2, 3]。20世纪90年代初, Birx等[4]首先将混沌振子应用到信号检测, 这种基于混沌振子的检测方法可以检测更低信噪比下的微弱信号, 且不会对有用信号产生影响。
Duffing振子系统是产生混沌现象的一类常用非线性系统, 具有对噪声的免疫性和对微弱信号的敏感性, 可实现低信噪比下的微弱信号检测[5, 6, 7]。然而, 将基于Duffing振子的检测方法应用到低信噪比下的信号检测中存在几个关键性问题:①Duffing振子系统处于临界状态下时, 一定强度的输入噪声可能对系统产生扰动, 改变系统运动状态, 造成信号检测结果的误判; ②输入信号中目标信号相位与系统中内策动力的相位需同步才能产生目标信号对系统的有效扰动, 而输入信号相位在实际中是未知的, 因而可能造成漏检; ③如何实现Duffing振子输出运动状态低运算量、高精度的嵌入式判断。
本文分析了输入信号中噪声的强度对临界状态下Duffing振子系统运动状态的影响, 基于临界阈值随噪声强度减小而单调递减这一特性, 提出了依托临界阈值字典的逆向相变方法, 解决了低信噪比下由于噪声对检测系统的扰动而产生误判的问题。通过公式推导, 分析了目标信号相位对检测结果的影响, 提出了一种双振子联合检测方式, 解决了低信噪比下相位同步问题对检测的影响。根据Duffing振子检测过程中相空间图形的变化, 提出了一种基于点集拓扑理论的系统运动状态判断方法, 并证明了其可行性, 实现了系统输出运动状态低运算量、高精度的嵌入式判断。基于以上方法, 最终得到了一种更加适用于工程实际的低信噪比下Duffing振子检测模型, 并得出了最低检测信噪比。
Duffing振子系统是单位质量为1的粒子在势场中受外场作用力、阻尼力和势场作用力共同作用而产生的轨迹运动方程。
检测系统表述为:
式中:
在稳定内策动力下, 取
系统处于混沌到大尺度周期的临界状态时, 输入信号中的噪声成分可能对系统产生扰动, 使系统从临界状态运动到大尺度周期状态, 导致无法准确判断目标信号是否存在。式(1)所示Duffing振子信号检测系统临界状态内策动力幅值为0.720 649 12, 逐一减少小数点后临界阈值的位数, 分别进行100次蒙特卡罗实验, 得到不同输入噪声强度下临界阈值精度
方差值为6时, 仅临界值精度为小数点后一位时, 噪声对系统运动状态无影响; 方差值小于6时, 噪声对系统运动状态的影响具有很强的随机性, 仅当临界阈值精度为0.1时, 噪声的输入对系统运动状态无影响。对于式(1)所示的检测系统, 若采用文献[9]中的方法, 设定临界阈值为0.7, 能检测到幅值大于0.02的目标信号, 最低检测信噪比为-13.01 dB, 而本文试图检测到更低信噪比下的信号。
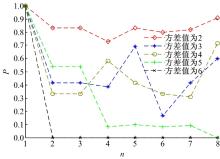
固定临界状态幅值为0.720 649, 改变方差大小, 得到相态不变的概率曲线, 如图2所示。固定临界状态幅值, 不同噪声强度下, 噪声对系统的影响并非确定的。仅噪声方差值为0, 即方差为1时, 蒙特卡罗实验结果得到的相态不变概率为1, 然而实际检测中并不能确保噪声的强度为1。
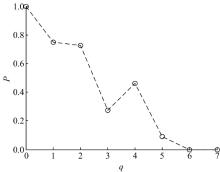 | 图2 临界状态下输入噪声强度对系统输出状态的影响Fig.2 Influence of input signal intensity on system output state under critical state |
基于以上问题, 文献[11]中提出了针对噪声影响的逆向相变方法; 文献[12]中将噪声对系统的扰动归因于过渡带的存在, 设计了一种新的方程形式, 改善了临界相变过渡带的影响, 而两种方法应用于信号检测均要改变临界阈值。文献[12]所述方法需在检测过程中反复确认新方程的两个临界阈值, 使得检测过程复杂度大大提高, 本文基于文献[11]中的逆向相变方法, 制定临界阈值字典, 使上述噪声问题得到解决。
逆向相变方法是基于Duffing振子的相反过程, 系统的初始状态设定为大尺度周期状态, 大尺度周期状态到混沌状态的临界阈值为
从文献[11]中得知:输入信号中的噪声成分达到一定强度后, 会使得临界状态的系统随机地发生相变, 随着噪声强度的增加, 正向、逆向相变对内策动力幅度的分辨能力都有所降低, 正向相变临界阈值有所降低, 而逆向相变临界阈值有所升高。在利用Duffing振子系统进行检测时, 输入噪声后相态不变的临界阈值才是可用于检测的有效值, 而上述临界阈值是随着噪声强度的变化而改变的, 实际中每次检测都要根据噪声强度估算临界阈值是不现实的, 本文根据临界阈值的变化规律提出一种基于临界阈值字典的改进方法, 使得逆向相变方法得以应用到实际检测中。
设输入信号为纯噪声, 分析临界阈值随噪声强度的变化规律。噪声强度依然用方差值表示, 如图3(a)所示。为了能更直观地观察出噪声强度与临界阈值的关系, 对方差值为5~7时的临界阈值图像进行放大, 如图3(b)所示。
随着方差值的增大(即噪声强度减小), 临界阈值单调递减, 且由临界阈值的大小可以看出:随着噪声强度减小, 临界阈值精度提高, 如噪声强度为-30 dB时, 临界阈值为0.723; 噪声强度为-60 dB时, 临界阈值为0.719 922 3。
仿真研究表明, 对于初值、Duffing方程系数确定的检测系统, 仅噪声强度变化对系统临界阈值有影响, 与目标信号
要实现上述字典调用方法, 首先要对输入信号进行噪声强度估计[13, 14]。
其次, 对于本文中的输入信号:
制定临界阈值字典, 步骤如下:
(1)对式(1)表示的检测模型, 输入纯噪声信号
(2)进行n=100次蒙特卡罗实验, 得到强度为Pa的噪声导致系统相变的概率Pc和对应的临界阈值L, 当
(3)以一定的步长间隔分别将不同强度的噪声输入系统, 如步长m=5, 输入强度为5、0、-5、-10 dB, …的噪声, 重复上述步骤, 即可得到不同噪声强度对应的临界阈值字典。
(4)将噪声强度和临界阈值进行对应存储。
如需更加精确的检测, 只需按照需求增大蒙特卡罗实验次数n或减小步长m。基于上述方法通过仿真可知, 在步长为10的字典中, 最低可以检测到目标信号幅值为0.000 699。
以上讨论中假设策动力相位与目标信号相位的差为零, 而实际检测时并不能保证两者具有相同的相位, 目标信号相位对检测结果的影响也是利用Duffing振子进行信号检测时需解决的一个问题。文献[9]中采用不同输入、不同内策动力相位的4个检测系统实现了对任意相位输入信号的检测。引入文献[15]中的相位补偿思想, 本文提出双振子联合检测方法。
对于式(1)表示的Duffing振子检测系统, 设策动力相位为
式中:ϕ , φ ∈ [-π , π ], 文献[9]中变尺度方法可实现策动力频率与目标信号频率的统一, 故而此处令
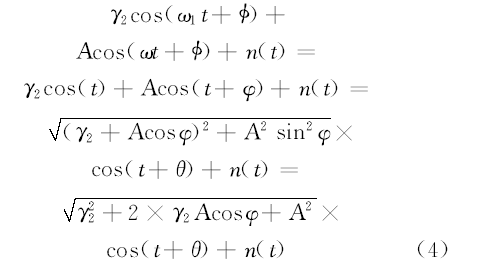
式中:
弱信号输入时
因此
设临界阈值为
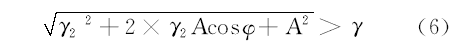
推导可得:
同样地, 对于
由于φ ∈ [-π , π ], 由三角函数的周期性可得:当
在输入信号相位未知的前提下, 仅考虑相位差异, 系统对目标信号的检测概率只有50%。为了消除这一影响, 引入内策动力相位补偿的思想, 令内策动力相位为-π , 则有:
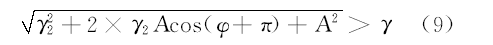
故而此时:
由以上推导可知, 对于弱输入信号, 引入内策动力相位进行补偿可达到对周期内所有相位的目标信号检测的目的。利用如式(11)和(12)所示的双Duffing振子检测系统进行联合检测, 分别命名为系统1和系统2:
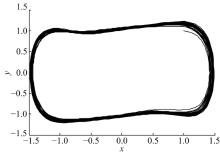
对未知相位的单频信号进行检测, 同时分析系统1和系统2的输出, 如图4图5所示。由于是逆向检测, 图4大尺度周期状态为相不变状态, 图5混沌状态为相变状态, 系统1和系统2的输出中有一个产生相变即判定为存在目标信号。
以上推导过程中式(8)~(10)均基于
对于如式(1)所示的检测系统, 由以上分析可知, 临界阈值稳定在0.72左右, 取临界阈值为0.72, 可检测到输入信号幅值为0.01时的单频信号, 得到:
故当目标信号幅度为0.01时, 检测概率为:
同理可得信号幅度0.001时, 检测概率为99.999%。随着信号幅度的减小, 信号幅度与临界阈值的比值降低, 检测概率提高, 越来越接近1。本方法适用于远距离下能量损耗较大的弱信号的检测。
从以上分析可以看出, Duffing振子检测方法是基于辨识系统输出运动状态改变来实现的, 而最终判断系统运动状态为相空间图像观察方法, 这种方法不适用于工程实际, 要将Duffing振子检测方法应用于工程实践, 需将系统运动状态判断方法转化为机器语言以实现检测结果的嵌入式表征。
文献[16]中采用了Melnikov方法, 求解比较简单但是判别准确性较低。文献[17]中的Lyaponov方法对于含有噪声的Duffing振子输出相空间效果较差。文献[18]中采用了Poincare截面法, 具有较好的相空间抗噪性能, 但是要经过一阶方程转化, Poincare截面转化等步骤, 比较繁琐。为了解决这一问题, 本文结合点集拓扑理论, 针对Duffing振子检测系统输出相空间的拓扑特性的差异, 提出了一种低信噪比下高准确率、低运算量的Duffing振子运动状态判别方法。
式(1)所示的Duffing振子检测系统中, 固定参数k, 改变A或
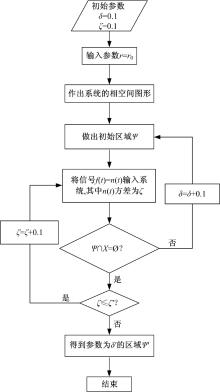
首先要确定上述的判定区域, 具体流程如图6所示, 其中方差
且不必与待测信号中所含噪声方差相等。其中
相空间上的点对应于式(1)所示Duffing振子检测系统时域两个输出x、y的值形成的数对, 即
混沌检测系统的输出相空间
有界性:对于式(1)所示Duffing振子检测系统,
输出相空间中
设方程(17)的解为
解微分方程组(18)可得到
式中:
同理可证,
距离空间
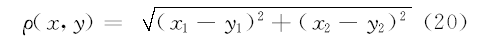
由以上分析可知, 在如式(20)的度量下,  , 为有界子集, 由点集拓扑理论中有界度量空间定义可知,
, 为有界子集, 由点集拓扑理论中有界度量空间定义可知,
列紧性:显然, 相空间X是2维欧式空间
设信号和噪声同时输入系统时形成的拓扑空间为
若
则称
设
在距离
连接上述4点, 形成一个集合
存在
式(23)所示
故而, 线性流形
设
结合以上证明, 有界且列紧的拓扑空间内, 必有:
取
由以上分析可知, 同参数下相同系统输出相空间的拓扑空间边界范围相同, 故而对于一个检测系统, 仅确定一次判定区域即可。
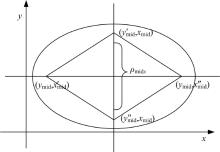
由图7可知, 最终确定的判别区域为四条直线构成的菱形, 表述为:
判别时, 将相空间点代入式(16)左侧, 比较与1的大小关系。此处涉及到2× 4次除法运算记为C, 1× 4次加法运算记为J, 1× 4次大小比较记为B。实际判别过程中, 首先确定大尺度周期状态下输出信号的周期记为T, 从第一个数对开始, 每隔一个周期取下一个数对进行判断, 如上所述, 若第
除法、加法和大小比较在Matlab等软件中均容易实现且运算时间很短, 本判别方法具有较小的复杂度。
为了分析判别方法的性能, 在不同精度的临界r值下, 分别进行100次蒙特卡罗实验, 统计出可以正确判断运动状态的次数, 如表1所示。
| 表1 判别性能 Table 1 Performance of judgment |
由表 1可知, 临界r值达到小数点后六位以后图形方法存在误判。经仿真分析表明, 当r取值较为精确时, 由于硬件精度有限, 系统本应处于混沌临界状态, 所得相空间图形却表现为大尺度周期状态, 从而出现了小概率误差。临界值r的小数点后达到八位或更多时, 由于方程解法精度限制和硬件条件限制, 混沌检测系统对单频信号不再敏感, 无法完成检测。
基于以上对利用Duffing振子进行信号检测时存在的问题分析, 解决了噪声影响、相位影响和运动状态判断3个关键问题, 建立Duffing振子信号检测模型, 如图8所示。
将本文提出的逆向字典方法噪声强度值步长定为1, 采用宽带噪声进行仿真, 带宽为1~10 kHz, 对于2 kHz的单频信号, 利用变尺度方法将目标信号频率变化到1 Hz, 相应的宽带噪声频率变化为0.5~5 Hz。根据以下信噪比计算公式:
式中:A为输入信号幅值;
本文提出的逆向联合检测系统最低检测信噪比(-36.99 dB)远低于文献[9]中所述方法的最低检测信噪比(-13.01 dB)。
本文针对Duffing振子检测系统中临界状态下一定强度的噪声对系统产生扰动、待测信号与系统策动力的相位需同步、Duffing振子运动状态判断3个关键问题, 提出了一种逆向联合Duffing振子信号检测模型。提出了一种基于临界阈值字典的逆向相变方法, 基于临界阈值的单调性, 建立临界阈值字典, 解决了低信噪比下噪声对系统产生扰动的问题; 提出了一种双系统联合检测方法, 利用两个策动力相位互异的Duffing振子检测系统联合检测, 解决了待测信号相位和策动力相位的同步问题, 并计算出了由于相位的不遍历性导致的虚惊概率; 提出了一种基于输出相空间形态的Duffing振子检测系统运动状态表征方法, 并进行了可行性的数学证明, 实现了检测结果的低运算量、高精度嵌入式表征。最终建立了较完整的Duffing振子检测模型, 得出最低检测信噪比为-36.99 dB。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|