基于纵向频响特性的整车质量估计

引用本文

胡满江, 罗禹贡, 陈龙, 李克强. 基于纵向频响特性的整车质量估计[J].吉林大学学报（工学版）, 2018,48(4): 977-983
HU Man-jiang, LUO Yu-gong, CHEN Long, LI Ke-qiang. Vehicle mass estimation based on longitudinal frequency response characteristics[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 977-983 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170313
Permissions

基于纵向频响特性的整车质量估计

胡满江, 罗禹贡, 陈龙, 李克强

清华大学汽车安全与节能国家重点实验室,北京 100084

通讯作者:陈龙(1989-),男,博士研究生.研究方向:智能网联汽车安全应用.E-mail:844270871@qq.com

作者简介:胡满江(1988-),男,助理研究员,博士研究生.研究方向:整车技术集成与安全应用.E-mail:manjiang_h@vip.163.com

基金:国家自然科学基金项目(51505247).

摘要

为了能够实现对不同车辆质量的通用型估计,提出了一种基于纵向频响特性的整车质量估计方法。该方法通过智能网联汽车普遍获取的纵向加速度和车轮转速信息,基于车辆纵向动力学模型,推导出加速度与轮速信号间的幅频函数关系,并求取在不同频率下车辆质心处加速度与轮速之间的幅值比,进而通过最小二乘法拟合得到整车质量。CarSim-Simulink联合仿真结果表明:本文的整车质量估计方法精度在93.9%以上,可满足多车协同避撞系统车辆控制的要求。

关键词: 车辆工程; 整车质量估计; 纵向动力学模型; CarSim-Simulink联合仿真; 智能网联汽车; 多车协同避撞

中图分类号:U461.91 文献标志码:A 文章编号:1671-5497(2018)04-0977-07

Vehicle mass estimation based on longitudinal frequency response characteristics

HU Man-jiang, LUO Yu-gong, CHEN Long, LI Ke-qiang

State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China

Abstract

A vehicle mass estimation method based on longitudinal frequency response characteristics is proposed for wide application for different types of vehicles. First the longitudinal acceleration and wheel speed information obtained from intelligent connected vehicle are used to derive the amplitude-frequency function between acceleration and wheel speed signal based the vehicle longitudinal dynamics model. Then, the amplitude ratio of the acceleration of the center of mass to the wheel speed at different frequencies is obtained. Finally the vehicle mass is calculated by least square fitting. The CarSim-Simulink co-simulation results show that the estimation accuracy of the proposed method is above 93.9%, which can meet the requirement of vehicle control for multi-vehicle coordinated collision avoidance system.

Keyword: vehicle engineering; vehicle mass estimation; longitudinal dynamics model; CarSim-Simulink co-simulation; intelligent connected vehicle; multi-vehicle coordinated collision avoidance

文章图片

0 引言

车辆状态数据是实现多车协同避撞控制逻辑和下层控制方法的基础和前提^[1], 而整车质量作为控制期望输出力与车辆加速度间的惯性连接参数, 其估计精度的准确与否影响着车辆的控制响应^[2]。整车质量和道路坡度对于车辆纵向运动的影响是同时存在的, 相关研究通常是实现两者的联合估计; 或者先估计坡度, 再估计质量。坡度的估计可以借助运动学方法实现, 如利用车辆纵向速度的变化率, 纵向加速度传感器测量值和道路坡度间的运动学关系, 还可以利用GPS测量行驶的距离, 结合大气压力传感器测量出的海拔变化, 得到车辆行驶道路的坡度角^[3]。Eriksson^[4]基于整车纵向动力学方程, 假定坡度已知, 通过测量发动机扭矩, 利用卡尔曼滤波观测器^[5]实现质量估计, 如果道路坡度变化, 则该方法会出现较大误差。Vahidi等^{[6, 7, 8]}利用最小二乘法实现质量和坡度的同时估计。McIntyre等^[9]尝试利用模型预测控制方法估计质量。Winstead等^[10]应用李雅普诺夫方法, 设计了卡尔曼滤波观测器与模型预测控制器联合估计的自适应滤波器, 理论上保证了观测器的稳定性。同济大学冯源等^[11]首先利用轴荷分配规律排除道路坡度的影响, 进而结合轮毂电机驱动转矩精确可知的特点, 以分阶段式的最小二乘法实现质量估计。北京航空航天大学王健等^[12]在线性二自由度单轨车辆模型的基础上, 建立了滑膜观测器估计车辆的质心侧偏角。清华大学Chu等^[13]采用高频信息提取的方法, 实现了质量与坡度间的解耦估计。上述辨识控制对象关键参数的观测方法均需要车辆处于较大激励, 而智能网联汽车通常会在智能底盘集成控制^[14]下处于稳态区域, 仅依靠传统时域信息的观测方法难以在近稳态激励下剥离其他参数对待估计参数的影响。

为此, 本文提出了基于频响特性的车辆关键参数辨识方法来实现整车质量估计。利用智能车辆上广泛装配的加速度传感器和轮速传感器采集纵向加速度信号和车轮转速信号; 基于整车纵向动力学方程, 推导出加速度与轮速信号间的幅频函数, 求取在不同频率下车辆质心处加速度与轮速之间的幅值比, 进而通过最小二乘法拟合得到整车质量最佳估计值表达式; 最后基于CarSim-Simulink联合仿真验证了该方法的准确性。

1 道路纵向坡度与整车质量解耦

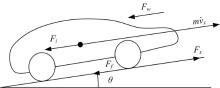
车辆纵向加速度是由驱动力、空气阻力、坡道阻力、滚动阻力等内外力综合作用引起的, 如图1所示, 其中 $F_{i} 为汽车坡度助力, F_{f} 为滚动助力, F_{w}$ 为来自空气的空气阻力。

	Figure Option View Download New Window
	图1 整车纵向动力学示意图Fig.1 Schematic diagram of vehicle longitudinal dynamics

车辆的纵向动力学模型可简化为如式(1)所示。

$\begin{array}{l} F_{x} = m {\overset{\cdot}{v}}_{x} + \frac{1}{2} ρ C_{d} A v_{x}^{2} + \\ mg (\sin θ + f \cos θ) \end{array}$ (1)

式中: $F_{x}$ 为轮胎瞬时纵向驱动力; $m$ 为整车质量; $v_{x}$ 为车辆质心处的纵向速度; ${\overset{\cdot}{v}}_{x}$ 为车辆质心处的纵向加速度; $ρ$ 为空气密度, $C_{d}$ 为空气阻力系数; $A$ 为车辆纵向迎风面积; $g$ 为重力加速度; $θ$ 为路面坡度; $f$ 为路面滚动阻力系数。

将式(1)左、右两端同时对车辆纵向加速度 ${\overset{\cdot}{v}}_{x}$ 采用微分运算, 可得:

$\begin{array}{l} \frac{d F_{x}}{d {\overset{\cdot}{v}}_{x}} = m + ρ C_{d} A v_{x} \frac{d v_{x}}{d {\overset{\cdot}{v}}_{x}} + \\ mg (\cos θ - f \sin θ) \frac{d θ_{x}}{d {\overset{\cdot}{v}}_{x}} \end{array}$ (2)

从较长距离看坡度一般为定值(除特殊情况外), 且与车辆纵向加速度不直接相关, 而坡度的瞬时变化是随机的, 可以看作为噪声项, 故道路坡度对纵向加速度的微分为零:

$\frac{d θ}{d {\overset{\cdot}{v}}_{x}} = 0$ (3)

动力传动系统的驱动力矩一般有较高的变化频率, 相比之下, 纵向加速度的积分值— — 纵向车速的变化率要远小于加速度变化率。与纵向加速度的微分信号相比, 可以认为纵向速度的微分信号是很小的量, 即:

$\frac{d v}{d {\overset{\cdot}{v}}_{x}} = 0$ (4)

综合式(3)(4), 式(3)可以简化为式(5):

$m \approx \frac{d F_{x}}{d {\overset{\cdot}{v}}_{x}}$ (5)

由式(5)可知, 当驱动力的变化率较大时, 空气阻力、坡道阻力和滚动阻力对质量估计的影响可忽略不计, 即完成了道路纵向坡度与整车质量两者估计过程的解耦。

2 整车纵向动力学频响特性

在车辆智能安全系统中普遍运用的车辆状态信号主要包含纵向加速度、轮速等信号。若整车质量可由这两种信号估计得出, 这种方法将获得在不同智能车辆架构下的普遍适用性。为此, 本部分将结合式(5)进一步推导纵向加速度与轮速的频域关系。

式(5)右侧的分母和分子同时对时间进行微分, 可得:

$m = \frac{d F_{x}}{d {\overset{\cdot}{v}}_{x}} = \frac{d F_{x} / d t}{d {\overset{\cdot}{v}}_{x} / d t} = \frac{{\overset{\cdot}{F}}_{x}}{{\overset{\cdot \cdot}{v}}_{x}}$ (6)

进一步整理可得轮胎瞬态纵向力微分式为:

${\overset{\cdot}{F}}_{x} = m {\overset{\cdot \cdot}{v}}_{x}$ (7)

将式(7)左、右两侧同时乘以时间延迟系数 $τ,$ 并与式(1)求和, 可得:

$\begin{array}{l} τ {\overset{\cdot}{F}}_{x} + F_{x} = τm {\overset{\cdot \cdot}{v}}_{x} + m {\overset{\cdot}{v}}_{x} + \\ \frac{1}{2} ρ C_{d} A v_{x}^{2} + mg (\sin θ + f \cos θ) \end{array}$ (8)

式(8)左、右两端同时对车辆纵向加速度 ${\overset{\cdot}{v}}_{x}$ 采用微分运算, 可得:

$\begin{array}{l} \frac{d (τ {\overset{\cdot}{F}}_{x} + F_{x})}{d {\overset{\cdot}{v}}_{x}} = \frac{d (τm {\overset{\cdot \cdot}{v}}_{x} + m {\overset{\cdot}{v}}_{x})}{d {\overset{\cdot}{v}}_{x}} + \\ ρ C_{d} A v_{x} \frac{d v_{x}}{d {\overset{\cdot}{v}}_{x}} + mg (\cos θ - f \sin θ) \frac{d θ}{d {\overset{\cdot}{v}}_{x}} \end{array}$ (9)

结合式(3)(4), 式(9)可以简化为式(10):

$\begin{array}{l} \frac{d (τ {\overset{\cdot}{F}}_{x} + F_{x})}{d {\overset{\cdot}{v}}_{x}} = \frac{d (F_{x}^{S})}{d {\overset{\cdot}{v}}_{x}} = \\ \frac{d (k_{s} s + F_{x 0})}{d {\overset{\cdot}{v}}_{x}} \approx \frac{d (τm {\overset{\cdot \cdot}{v}}_{x} + m {\overset{\cdot}{v}}_{x})}{d {\overset{\cdot}{v}}_{x}} \end{array}$ (10)

式中: $F_{x}^{S} 为车轮稳态纵向力; k_{s} 为车轮纵向刚度; F_{x 0}$ 为滑移率为0时的纵向力。

式(10)左、右两侧的分母和分子同时对时间进行微分, 可得:

$\begin{array}{l} \frac{d (k_{s} s + F_{x 0}) / d t}{d {\overset{\cdot}{v}}_{x} / d t} = \frac{k_{s} \overset{\cdot}{s}}{{\overset{\cdot \cdot}{v}}_{x}} \approx \\ \frac{d (τm {\overset{\cdot \cdot}{v}}_{x} + m {\overset{\cdot}{v}}_{x}) / d t}{d {\overset{\cdot}{v}}_{x} / d t} = \frac{τm {\overset{\dots}{v}}_{x} + m {\overset{\cdot \cdot}{v}}_{x}}{{\overset{\cdot \cdot}{v}}_{x}} \end{array}$ (11)

对式(11)进一步整理可得:

$k_{s} \overset{\cdot}{s} = τm {\overset{\dots}{v}}_{x} + m {\overset{\cdot \cdot}{v}}_{x}$ (12)

结合驱动工况下, 轮胎滑移率的定义:

$\{\begin{array}{l} F_{x}^{S} = k_{s} s + F_{x 0} \\ s = \{\begin{array}{l} \frac{Rω - v_{x}}{v_{x}}, 制动工况 \\ \frac{Rω - v_{x}}{Rω}, 加速工况 \end{array} \end{array}$ (13)

式中: $R$ 为没有地面制动力时的车轮滚动半径。

可将式(12)写成式(14):

$\begin{array}{l} k_{s} \overset{\cdot}{s} = k_{s} (\frac{Rω - v_{x}}{Rω}) \frac{'}{} = \\ k_{s} \frac{R \overset{\cdot}{ω} v_{x} - {\overset{\cdot}{v}}_{x} Rω}{{(Rω)}^{2}} = τm {\overset{\dots}{v}}_{x} + m {\overset{\cdot \cdot}{v}}_{x} \end{array}$ (14)

由于智能群体中单车通过智能驾驶系统将自身控制在稳定区域, 即轮胎侧偏角或者滑移率很小。那么可假设 $Rω \approx v_{x}$ , 由于车辆的惯性远大于车轮的惯性, 因此车辆的加速度相比车轮的角加速度可以忽略。基于此, 进一步整理(14)可得:

$k_{s} \frac{R \overset{\cdot}{ω}}{v_{x}} = τm {\overset{\dots}{v}}_{x} + m {\overset{\cdot \cdot}{v}}_{x} = τm {\overset{\cdot \cdot}{a}}_{x} + m {\overset{\cdot}{a}}_{x}$ (15)

对式(15)两侧进行拉布拉斯变化, 可得:

$\frac{k_{s} R}{v_{x}} λω (λ) = τm λ^{2} a_{x} (λ) + mλ a_{x} (λ)$ (16)

对(16)整理, 可得两个状态量间的传递函数为:

$\frac{ω (λ)}{a_{x} (λ)} = \frac{m v_{x}}{k_{s} R} (τλ + 1)$ (17)

式(17)为车辆质心处加速度与车轮轮速之间的频率关系表达式。

3 本文方法

通过式(17)可知, 车辆质心处加速度与轮速之间的频率关系是与整车质量有关的。假设车速为已知信号, 轮胎半径为已知参数, 式(17)右侧仅整车质量为未知。为此, 首先利用周期图法(Welch's averaged periodogram method)^[15]求取在不同频率下, 车辆质心处加速度与轮速之间的幅值比, 进而通过最小二乘法拟合得到整车质量。

(1)幅值比的求取方法采用下式:

$Z (ω |a_{x}) = \frac{S_{a_{x} ω}}{S_{a_{x} a_{x}}}$ (18)

式中: $Z (ω |a_{x})$ 为不同频率下车辆质心处加速度与轮速之间的幅值比; $S_{a_{x} ω}$ 为加速度与轮速的互功率谱密度; $S_{a_{x} a_{x}}$ 为加速度的自功率谱密度。

通过式(18)可以得到在不同频率下的幅值比, 设 $f_{i}$ 为频率采样点 $i$ 的频率值; $A_{i}$ 为频率采样点 $i$ 的幅值比。

(2)以式(17)为基础, 令 $λ = (- 2 π f) j, f$ 为频率, 推导出幅频函数如下:

$\frac{A_{\omega}(f)}{A_{a_{x}}(f)}$=$\frac{m_{v_{x}}}{K_{s}R}\sqrt{(2\pi \tau f)^{2}}+1$(19)

(3)令 $x_{i}$=$\frac{v_{x}}{K_{s}R}\sqrt{(2\pi \tau f_{i})^{2}+1}$, $y_{i}=A_{i}$。采用最小二乘法估计参数时, 要求观测值 $y_{i}$ 的偏差的加权平方和最小。对于本文的待估计参数质量来说, 可使下式的值最小:

$\overset{N}{\sum_{i}} {(y_{i} - m x_{i})}^{2}$ (20)

式中: $N$ 为选取的频率样本数。

式(20)对 $m$ 求导得:

$\frac{d}{d m} \overset{N}{\sum_{i}} {(y_{i} - m x_{i})}^{2} = - 2 \overset{N}{\sum_{i}} (y_{i} - m x_{i}) x_{i} = 0$ (21)

求解式(21), 即可得到整车质量的最佳估计值如下:

$\hat{m} = \overset{N}{\sum_{i}} y_{i} x_{i} / \overset{N}{\sum_{i}} x_{i}^{2}$ (22)

4 仿真验证

利用CarSim-Simulink联合仿真平台验证基于整车纵向频响特性的整车质量估计方法, 仿真车辆参数设置如表1所示。

表1 仿真车辆主要参数 Table 1 Main vehicle parameters in simulation

4.1 轮速与纵向加速度间传递函数验证

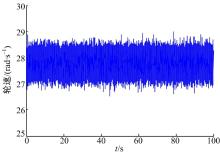
验证轮速与纵向加速度之间的传递函数, 即式(19)。设置质量 $m$ 为2000 kg。在仿真平台中输入从0.1~5 Hz的扫频轮速信号, 如图2所示。

	Figure Option View Download New Window
	图2 仿真中轮速扫频信号Fig.2 Vehicle wheel swept-frequency signal in simulation

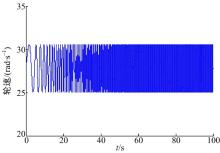
从图2中可以看出, 轮速的稳态值为27.8 rad/s, 扫频幅值为2.78 rad/s。扫频幅值相比稳态值较小且频率较高, 可以推断车辆应近似匀速行驶。受此信号驱动下, 得到的纵向速度信号如图3所示。

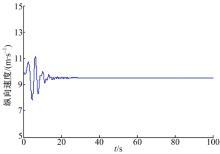
	Figure Option View Download New Window
	图3 仿真中纵向速度信号Fig.3 Vehicle longitudinal speed signal in simulation

从图3可知, 在20 s之前, 由于轮速扫频的频率较低, 车速能够跟随轮速进行微小变化。随着频率的增大, 车速趋于稳定, 收敛于9.5 m/s。这样就符合了质量估计公式推导过程中的假设条件之一(见式(4)), 即车速变化速率远小于轮速的变化率。因此仅关注20 s以后的加速度信号, 如图4所示。

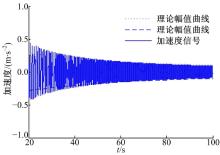
	Figure Option View Download New Window
	图4 仿真的加速度信号Fig.4 Vehicle acceleration signal in simulation

从图4可以看出, 加速度小于0.5 m/s², 符合质量估计公式推导过程中的另一假设条件(见式(14)(15)), 即轮胎处于小滑移率范围。图4中, 虚线和划线是结合扫频信号频率与时间的关系, 由式(19)计算得到的加速度幅值-时间曲线。对比该曲线和仿真加速度信号的峰值点可以发现, 两者较好地重合在一起, 表明式(19)可以精确地描述在不同频率下的轮速与加速度间的幅值关系。

4.2 基于周期图法的整车质量估计

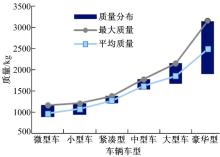
为验证基于纵向频响特性整车质量估计方法的准确性和适应性, 考虑到与商用车及其他车辆相比, 乘用车具有较高的智能化装配率, 为此, 对市场上在售的不同类型乘用车^[16]整车装备质量进行调研, 将每种车辆类型中销量前10名的车型整车装备质量进行统计, 根据调研结果, 质量分布如图5所示, 统计结果见表2。

	Figure Option View Download New Window
	图5 整车装备质量分布Fig.5 Vehicle total mass distribution

表2 整车装备质量统计 Table 2 Vehicle total mass statistic

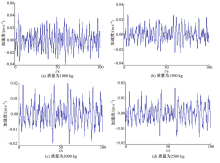
在质量估计方法理论核心, 即式(19)成立的基础上, 基于周期图的方法, 实现质量估计。在正常匀速行驶时, 轮速可以看作以随机信号。在仿真平台中构造随机的轮速信号, 如图6所示。根据上述整车质量分布与统计情况表, 分别设置仿真整车质量为1000、1500、2000和2500 kg。在图6信号作用下, 获得在不同整车质量设置下的加速度信号, 如图7所示。

	Figure Option View Download New Window
	图6 随机轮速信号Fig.6 Random wheel speed signal

	Figure Option View Download New Window
	图7 不同质量下的加速度信号Fig.7 Acceleration signals in different mass

对比图7(a)~(d), 可以看出质量增加导致了加速度在同等随机输入下振荡幅值减小。基于加速度信号和轮速信号数据, 采用周期图法得到不同频率下的轮速与加速度的幅值比,

如图8所示。由图8可知, 不同质量下的轮速与加速度的幅值比原始数据点均与频率间存在近似线性关系, 这与式(19)是相吻合的。基于以上不同频率下的幅值比信息, 采用最小二乘法, 可得到整车质量估计值如表3所示。

	Figure Option View Download New Window
	图8 轮速与加速度的幅值比Fig.8 Amplitude ratio between wheel speed and acceleration

表3 整车质量估计结果 Table 3 Vehicle total mass estimation result

将利用式(22)得到的数值解带入到式(17), 并以此画出轮速与加速度间的幅值比-频率曲线, 与利用功率图法得到的参考值进行趋势对比, 如图8所示。可以看出:原始数据点均匀分布于拟合曲线周围。将质量估计值与对应参考值进行对比可得, 估计精度在93.9%以上。由此可见本文的质量估计方法精度较高且具有广泛的适应性。

5 结论

(1)利用纵向加速度信号和车轮转速信号, 基于整车纵向动力学方程, 推导出加速度与轮速信号间的幅频函数, 该函数与整车质量存在正相关特性。通过求取在不同频率下辆质心处加速度与轮速之间的幅值比, 采用最小二乘法拟合求得整车质量的最佳估计值表达式。

(2)采用CarSim-Simulink联合仿真验证了不同频率下的轮速与加速度间的幅值关系, 在此基础上, 根据实际整车装备质量统计结果, 对比整车质量估计值和理论值, 可得估计精度在93.9%以上, 表明本文的整车质量估计方法具有较高的准确性和适应性。

(3)本文着重从理论上探讨了该方法的可行性, 并利用仿真对方法进行了准确性验证。该方法在工程实践中的应用, 如目标车辆车轮转速信息的获取, 将在车辆智能化和网联化技术的工程应用中, 进行进一步的实践。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	节能与新能源汽车技术路线图战略咨询委员会, 中国汽车工程学会. 节能与新能源汽车技术路线图[M]. 北京: 机械工业出版社, 2016. [本文引用:1]
[2]	谢伯元, 王建强, 秦晓辉, 等. 基于车路协同的车辆状态估计方法[J]. 汽车工程, 2014, 36(8): 968-973. Xie Bo-yuan, Wang Jian-qiang, Qin Xiao-hui, et al. Vehicle state estimation based on V2I system[J]. Automotive Engineering, 2014, 36(8): 968-973. [本文引用:1]
[3]	Bae H S, Ryu J, Gerdes J C. Road grade and vehicle parameter estimation for longitudinal control using GPS[C]∥Proceedings of the IEEE Conference on Intelligent Transportation Systems, 2001: 25-29. [本文引用:1]
[4]	Eriksson A. Implementation and evaluation of a mass estimation algorithm[D]. Sweden: KTH Royal Institute of Technology, 2009. [本文引用:1]
[5]	Lingman P, Schmidtbauer B. Road slope and vehicle mass estimation using Kalman filtering[J]. Vehicle System Dynamics, 2002, 37: 12-23. [本文引用:1]
[6]	Vahidi A, Druzhinina M, Stefanopoulou A, et al. Simultaneous mass and time-varying grade estimation for heavy-duty vehicles[C]∥American Control Conference, Denver, Colorado, 2003: 4951-4956. [本文引用:1]
[7]	Vahidi A, Stefanopoulou A, Peng H. Experiments for online estimation of heavy vehicle's mass and time-varying road grade[C]∥ASME International Mechanical Engineering Congress and Exposition, Washington DC, USA, 2003: 451-458. [本文引用:1]
[8]	Vahidi A, Stefanopoulou A, Peng H. Recursive least squares with forgetting for online estimation of vehicle mass and road grade: theory and experiments[J]. Vehicle System Dynamics, 2005, 43(1): 57-75. [本文引用:1]
[9]	McIntyre M L, Ghotikar T J, Vahidi A, et al. A two-stage Lyapunov-based estimator for estimation of vehicle mass and road grade[J]. Transactions on Vehicular Technology, 2009, 58(7): 3177-3185. [本文引用:1]
[10]	Winstead V, Kolmanovsky I V. Estimation of road grade and vehicle mass via model predictive control[C]∥Proceedings of the IEEE Conference on Control Applications, Toronto, Canada, 2005. [本文引用:1]
[11]	冯源, 余卓平, 熊璐. 基于分段递推最小二乘估计的汽车质量辨识试验[J]. 同济大学学报: 自然科学版, 2012, 40(11): 1691-1697. Feng Yuan, Yu Zhuo-ping, Xiong Lu. Experimental research on partitioned recursive least squares estimation of vehicle mass[J]. Journal of Tongji University(Natural Science), 2012, 40(11): 1691-1697. [本文引用:1]
[12]	王健, 余贵珍, 张为, 等. 基于滑模观测理论的车辆质心侧偏角估算[J]. 北京工业大学学报: 自然科学版, 2011, 37(3): 335-341. Wang Jian, Yu Gui-zhen, Zhang Wei, et al. Vehicle sideslip angle estimation based on principles of sliding mode[J]. Journal of Beijing University of Technology(Natural Science Edition), 2011, 37(3): 335-341. [本文引用:1]
[13]	Chu W B, Cao K, Li S, et al. Vehicle mass estimation based on high-frequency-information extraction[C]∥IFAC Proceedings, 2013, 46(21): 72-76. [本文引用:1]
[14]	李静, 张家旭. 基于鲁棒 L₂ - L_∞/ H_∞的车辆底盘集成控制[J]. 吉林大学学报: 工学版, 2016, 46(6): 1757-1764. Li Jing, Zhang Jia-xu. Integrated control of vehicle chassis system based on robust L₂ - L_∞/ H_∞ method[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(6): 1757-1764. [本文引用:1]
[15]	Duhamel P, Vetterli M. Fast Fourier transforms: a tutorial review and a state of the art[J]. Signal Processing, 1990, 19(4): 259-299. [本文引用:1]
[16]	帅石金. 汽车文化[M]. 北京: 清华大学出版社, 2007. [本文引用:1]

2016

0.0

... 0 引言车辆状态数据是实现多车协同避撞控制逻辑和下层控制方法的基础和前提^[1],而整车质量作为控制期望输出力与车辆加速度间的惯性连接参数,其估计精度的准确与否影响着车辆的控制响应^[2] ...

2014

0.0

. 2014, 36(8):968-973

Vehicle state estimation based on V2I system

基于车路协同的车辆状态估计方法

Xie Bo-yuan , Wang Jian-qiang , Qin Xiao-hui

谢伯元, 王建强, 秦晓辉

2001

0.0

... 坡度的估计可以借助运动学方法实现,如利用车辆纵向速度的变化率,纵向加速度传感器测量值和道路坡度间的运动学关系,还可以利用GPS测量行驶的距离,结合大气压力传感器测量出的海拔变化,得到车辆行驶道路的坡度角^[3] ...

2009

0.0

... Eriksson^[4]基于整车纵向动力学方程,假定坡度已知,通过测量发动机扭矩,利用卡尔曼滤波观测器^[5]实现质量估计,如果道路坡度变化,则该方法会出现较大误差 ...

2002

0.0

2003

0.0

... Vahidi等^[6,7,8]利用最小二乘法实现质量和坡度的同时估计 ...

2003

0.0

... Vahidi等^[6,7,8]利用最小二乘法实现质量和坡度的同时估计 ...

2005

0.0

... Vahidi等^[6,7,8]利用最小二乘法实现质量和坡度的同时估计 ...

2009

0.0

... McIntyre等^[9]尝试利用模型预测控制方法估计质量 ...

2005

0.0

... Winstead等^[10]应用李雅普诺夫方法,设计了卡尔曼滤波观测器与模型预测控制器联合估计的自适应滤波器,理论上保证了观测器的稳定性 ...

2012

0.0

. 2012, 40(11):1691-1697 DOI:doi:10.3969/j.issn.0253-374x.2012.11.018

Experimental research on partitioned recursive least squares estimation of vehicle mass

基于分段递推最小二乘估计的汽车质量辨识试验

Feng Yuan , Yu Zhuo-ping , Xiong Lu

冯源, 余卓平, 熊璐

A new algorithm for vehicle mass estimation was studied based on the on road test of an in wheel motor vehicle. Containing the road gradient information in the longitudinal accelerometer signal, the algorithm removed the road grade from the longitudinal dynamics of the vehicle. Then, two different recursive least squares(RLS) schemes were proposed to estimate the driving resistance and the mass independently based on the acceleration partition. Experiments on the asphalt road, the plastic runway, and the gravel road as well as experiments with road grade were carried out. The estimation errors and the result convergence were analyzed. Then, according to several critical operating conditions, the adaptability of the algorithm was improved. The experimental data show that the estimation error is within 2.5% with various masses and different roads, which indicates that the algorithm can accurately estimate mass and its engineering application is valuable.

基于电动轮驱动电动汽车平台道路试验，对一种新的汽车质量辨识算法进行了研究.该方法根据加速度传感器能够测量沿测量轴的重力分量的特点，排除了坡度对质量辨识的影响；根据加速度分段方法，分别利用两段递推最小二乘算法得到行驶阻力及质量的估计值.在电动轮驱动电动汽车平台上分别进行了沥青、塑胶及碎石路面上以及坡道上的试验，分析了行驶阻力与质量辨识的误差与收敛情况，并针对几种特殊工况对算法进行适应性改进.试验结果显示，不同质量及道路状态下的估计误差均在2.5%以下，表明所设计的辨识算法具有很高的估计精度，具有良好的工程应用价值.

... 同济大学冯源等^[11]首先利用轴荷分配规律排除道路坡度的影响,进而结合轮毂电机驱动转矩精确可知的特点,以分阶段式的最小二乘法实现质量估计 ...

2011

0.0

. 2011, 37(3):335-341

Vehicle sideslip angle estimation based on principles of sliding mode

基于滑模观测理论的车辆质心侧偏角估算

Wang Jian , Yu Gui-zhen , Zhang Wei

王健, 余贵珍, 张为

... 北京航空航天大学王健等^[12]在线性二自由度单轨车辆模型的基础上,建立了滑膜观测器估计车辆的质心侧偏角 ...

2013

0.0

... 清华大学Chu等^[13]采用高频信息提取的方法,实现了质量与坡度间的解耦估计 ...

2016

0.0

... 上述辨识控制对象关键参数的观测方法均需要车辆处于较大激励,而智能网联汽车通常会在智能底盘集成控制^[14]下处于稳态区域,仅依靠传统时域信息的观测方法难以在近稳态激励下剥离其他参数对待估计参数的影响 ...

1990

0.0

... 为此,首先利用周期图法(Welch's averaged periodogram method)^[15]求取在不同频率下,车辆质心处加速度与轮速之间的幅值比,进而通过最小二乘法拟合得到整车质量 ...

2007

0.0

... 2 基于周期图法的整车质量估计为验证基于纵向频响特性整车质量估计方法的准确性和适应性,考虑到与商用车及其他车辆相比,乘用车具有较高的智能化装配率,为此,对市场上在售的不同类型乘用车^[16]整车装备质量进行调研,将每种车辆类型中销量前10名的车型整车装备质量进行统计,根据调研结果,质量分布如图5所示,统计结果见表2 ...