电子机械制动执行器的整体最优匹配设计

引用本文

夏利红, 邓兆祥. 电子机械制动执行器的整体最优匹配设计[J].吉林大学学报（工学版）, 2018,48(4): 998-1007
XIA Li-hong, DENG Zhao-xiang. Optimal design of electromechanical brake actuator through an integrated mechatronic approach[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 998-1007 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170507
Permissions

电子机械制动执行器的整体最优匹配设计

夏利红¹, 邓兆祥^1,²

1.重庆大学汽车工程学院,重庆 400044

2.重庆大学机械传动国家重点实验室,重庆 400044

通讯作者:邓兆祥(1962-),男,教授,博士生导师.研究方向:汽车底盘控制.E-mail:zxdeng@cqu.edu.cn

作者简介:夏利红(1986-),女,博士研究生.研究方向:汽车底盘主动控制设计技术.E-mail:x.lh.1986@163.com

基金:“863”国家高技术研究发展计划项目(2012AA111803); 重庆市科委科技攻关项目(cstc2012gg-yyjs0449); 机械传动国家重点实验室科研业务费专项项目(SKLMT-ZZKT-2012MS03).

摘要

以行星齿轮滚珠丝杆驱动式电子机械制动系统为研究对象,考虑动态阻力载荷、齿轮转动惯量及传动比离散性的影响,提出一种多约束条件下的两级传动机电系统的多目标最优匹配方法。首先,基于执行器的动力学模型和性能目标,针对紧急制动和高附着路面制动防抱死两种典型工况提出相应的负载特征和运动规律。接着,以电机和滚珠丝杆产品数据库为输入,以执行器尺寸限制、电机运行范围及滚珠丝杆性能需求为约束条件,选出能够驱动负载的所有滚珠丝杆和电机。然后,以太阳轮尺寸最小为目标,以齿轮齿面接触强度和齿根弯曲强度为约束条件,获取能够驱动负载的行星齿轮传动比和太阳轮齿数,获得数据库中满足条件的所有匹配方案。最终,获得同时考虑系统质量、启动加速度、制动间隙消除时间及电机等效输出力矩等目标的执行器多目标最优匹配方案。

关键词: 车辆工程; 行星齿轮滚珠丝杆驱动; 两级传动; 动态载荷; 电子机械制动执行器; 多约束多目标优化

中图分类号:U463 文献标志码:A 文章编号:1671-5497(2018)04-0998-10

Optimal design of electromechanical brake actuator through an integrated mechatronic approach

XIA Li-hong¹, DENG Zhao-xiang^1,²

1.School of Automotive Engineering, Chongqing University, Chongqing 400044, China

2.State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China

Abstract

A novel multi-objective optimal design method is proposed for gearhead and ball screw two-stage driven electromechanical Brake actuator (EMB). With consideration of important factors, such as two stage driving, discrete transmission ratio, dynamic resistant torque, transmission inertia and feasibility constraints related to the component characteristics, this method can applied to determine the optimal combination of motor, gearhead and ball screw. First, the loads and motion laws were analyzed based on the dynamic models of EMB for emergency braking and anti-lock braking on dry asphalt road. Then, all feasible motors and ball screws, which can drive the load and satisfy the requirement for actuator size, feasible torque and speed of motor, characteristics of the planetary gears and ball-screw, were selected among the catalogues. Second, the planetary gears were designed according to the combinations of feasible motors and ball-screws to minimize the size of the planetary gear with the constraints of Hertzian pressure and bending fatigue strength, respectively, thus all feasible combinations of motor, gar ratio and ball-screw were achieved. Finally, the multi-objective optimal combination was obtained with respect to actuator weight, starting acceleration, air gap closing time during braking, and motor output torque.

Keyword: vehicle engineering; gearhead and ball screw driven; two-stage driving; dynamic load; electromechanical brake actuator; multi-objective multi-constrained optimization

文章图片

0 引言

与传统液压制动系统相比, 电子机械制动系统(Electro-mechanical brake, EMB)在制动力控制方面的诸多优势吸引了国内外研究人员及企业的重视^{[1, 2, 3, 4, 5, 6]}。Bosch^[7]、Continental Teves^[8]、Delphi^[9]和PBR^[10]等公司分别提出了EMB执行器的不同结构, 其中驱动电机、齿轮减速器、将旋转运动转化为直线运动的运动转换机构是影响其性能的关键部件。目前关于执行器的匹配设计已有相关报道。杨坤^[11]和赵一博^[12]采用传统方法对EMB执行器进行了匹配设计, 但由于执行器的尺寸限制、电机运行范围及行星齿轮和滚珠丝杆的性能需求等未能综合考虑, 需要通过反复计算获得一种可行方案, 且并非最优方案。

由于传统方法存在局限性, 有研究人员针对电机和齿轮的最优匹配进行了研究。Pasch等^[13]以系统加速度最大和特定运动规律下运动时间最短为目标, 提出纯惯性载荷下的电机和减速器的最优匹配方法。Cusimano^[14]研究了负载运动规律对以电机等效连续输出力矩最小为目标的最优匹配的影响。上述研究均忽略了减速器的机械特性和阻力载荷的影响。之后, Cusimano^[15]考虑了动态阻力载荷及减速器转动惯量的影响, 以电机等效连续输出力矩最小为目标, 应用迭代方法得到特定运动规律下的电机和减速器的最优匹配。Giberti等^[16]考虑了齿轮的转动惯量和传动效率的影响, 以电机的运行范围和齿轮机械特性为约束条件, 以电机等效连续输出力矩最小为目标进行最优匹配, 发现齿轮的转动惯量和传动效率对最优匹配结果有显著影响。上述研究中齿轮的最优传动比是在连续域内求得的, 而现有齿轮的传动比往往是离散的。Roos等^[17]利用电机和齿轮的产品数据库, 以电机运行范围和齿轮的性能要求为约束条件在数据库中选出能够驱动负载的电机和齿轮组合, 并分别给出电机等效连续输出力矩、系统重量、峰值功率及系统能耗等最小化的匹配方案, 但在匹配时未考虑齿轮转动惯量和传动效率的影响。

关于电机与滚珠丝杆的最优匹配也有报道, Kim等^{[18, 19]}以滚珠丝杆导程、公称直径、控制增益等为选择变量, 以电机运行范围和滚珠丝杆弯曲载荷为约束条件, 以电机需求功率和系统惯量最小为目标, 实现了对滚珠丝杆驱动机电系统的多目标多约束下的整体最优匹配。Caracciolo^[20]不仅考虑了滚珠丝杆的性能需求和电机运行范围等约束条件, 同时将惯量比和控制带宽等影响系统闭环控制特性的参数也转化为约束条件, 实现了将多目标优化转化为以电机等效连续输出力矩最小为目标的单目标优化。

但是, 目前广泛应用的行星齿轮滚珠丝杆驱动式EMB执行器具有如下特点:①执行器为两级传动机电系统; ②执行器的工作负载复杂多变, 受到制动夹紧力控制和整车制动力控制的影响; ③执行器需要在满足负载响应速度的同时, 实现对系统质量和电机等效输出力矩的最小化。可见, EMB执行器的最优匹配是一个涉及两级传动、负载和运动规律复杂多变的多目标优化问题。但是, 之前的研究工作均是关于电机与齿轮或电机与滚珠丝杆之间的单级传动的匹配, 且未实现同时考虑动态负载和多约束条件下的多目标匹配优化。本文拟以行星齿轮滚珠丝杆驱动式EMB执行器为研究对象, 考虑动态阻力载荷、齿轮转动惯量及滚珠丝杆导程和行星齿轮传动比离散性的影响, 提出一种多约束条件下的两级传动机电系统的多目标最优匹配方法。

1 执行器的结构特征和动力学模型

1.1 执行器的结构特征分析

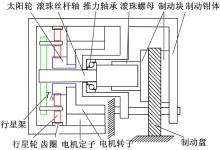
参照Wang设计的专利结构^[10]提出图1所示的行星齿轮滚珠丝杆驱动式EMB执行器的结构简图:分装式力矩电机的空心轴式转子和太阳轮固定链接, 转子内安装滚珠丝杆及推力轴承, 滚珠丝杆轴穿过太阳轮与行星架输出端链接。电机输出力矩经行星齿轮组放大后传递到滚珠丝杆轴, 将旋转运动转换为螺母的移动, 推动制动块压紧制动盘产生制动力。

	Figure Option View Download New Window
	图1 电子机械制动执行器结构方案简图Fig.1 Layout of proposed EMB actuator

1.2 单自由度动力学模型

基于刚性传动、集中参数的假设, EMB执行器的单自由度动力学方程为:

$T_{m} = J_{me} r \overset{\cdot \cdot}{x} + \frac{1}{r η_{g} η_{s}} F_{n}$ (1)

$J_{me} = J_{m} + J_{g} + \frac{J_{s}}{{i_{g}}^{2}} + \frac{1}{r^{2}} m_{n}$ (2)

$r = \frac{2 π i_{g}}{l}$ (3)

式中:T_m为电机输出力矩; J_me为系统等效转动惯量; r为系统总传递比, 即电机输入端转速与滚珠丝杆螺母移动速度的比值; $\overset{\cdot \cdot}{x}$ 为滚珠丝杆螺母的移动加速度; η _g为行星齿轮传动效率; η _s为滚珠丝杆传动效率; F_n为制动夹紧力; J_m为电机转动惯量; J_g为行星齿轮减速器等效到输入端的转动惯量; J_s为滚珠丝杆轴的转动惯量; i_g为行星齿轮传动比; m_n为滚珠丝杆螺母的质量; l为滚珠丝杆导程。

忽略温度和磨损的影响, 认为制动夹紧力F_n与制动块位移存在如下数学关系^{[3, 4]}:

$F_{n} = \{\begin{array}{l} 0, x \leq x_{ag} \\ K_{b} (x - x_{ag}), x > x_{ag} \end{array}$ (4)

式中:K_b为系统等效刚度, 根据文献[4]取值为3.30e7 N· m^-1; x为丝杆螺母的移动位移; x_ag为制动间隙。

2 匹配设计流程

执行器的性能目标、尺寸限制、负载特征、电机运行范围, 以及齿轮和滚珠丝杆的机械特性等影响整个执行器的匹配过程。图2(a)为传统设计方法的流程图, 可见传统设计过程为通过反复计算试错的方法获得一种可行方案而非最优方案匹配。图2(b)为一种整体最优匹配的设计方法。

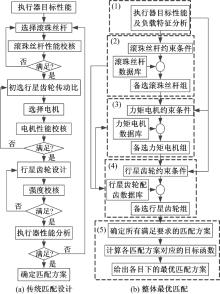	Figure Option View Download New Window
	图2 传统匹配设计方法和整体最优匹配方法Fig.2 Flow charts of conventional and currently proposed actuator selection procedure

整体最优匹配方法具体步骤如下:

(1)基于执行器的性能目标和动力学模型的分析, 提出紧急制动和高附着路面的制动防抱死(Anti-lock brake system, ABS)两种典型工况的负载和运动规律。

(2)以负载特征、尺寸限制及滚珠丝杆的性能需求为约束, 在产品数据中选出备选滚珠丝杆。

(3)根据尺寸限制初步确定行星齿轮的传动比范围, 结合备选滚珠丝杆的导程确定电机的运行范围, 在电机数据库中确定备选电机。

(4)以负载、备选电机和滚珠丝杆为输入, 以齿面接触疲劳强度和齿根弯曲疲劳强度需求为约束, 以太阳轮尺寸最小为目标, 完成与电机和滚珠丝杆相匹配的行星齿轮组的设计。

(5)分析所有满足条件的电机、滚珠丝杆及行星齿轮组合下的系统质量、启动加速度、制动间隙消除时间及电机等效连续输出力矩等目标参数, 得到各目标下的最优匹配方案。

该方法在匹配设计过程中综合考虑了执行器的尺寸限制、目标性能、负载和运动规律、电机运行范围以及齿轮和滚珠丝杆机械特性等约束, 可避免传统设计时的反复计算问题; 给出数据库中所有满足条件的匹配方案, 设计者可以根据特定目标选择相应的最优匹配方案。

3 约束条件

3.1 执行器的尺寸及性能目标约束

3.1.1 整体尺寸的约束

EMB执行器应满足轮毂内安装尺寸的限制, 同时应和悬架不产生干涉。配合项目需求, 为装有“ 雨燕” 车悬架和R15车轮的四轮独立制动的改装车(参数见表1)设计EMB执行器。根据轮毂内有效安装尺寸和悬架结构, 确定执行器的尺寸约束为:

$L \leq 205, H \leq 140, B \leq 200$ (5)

式中:L、H、B分为执行器的总长、宽、高, 单位为mm。

表1 整车参数 Table 1 Vehicle parameters

3.1.2 整体目标性能的约束

由于惯性力的作用, 后轮制动力小于前轮, 因此以前轮为例计算执行器的最大目标制动夹紧力。

单个执行器产生的最大制动器制动力应不小于单个车轮产生的最大地面制动力, 即:

$F_{μ \max} \geq α_{n} F_{bmax}$ (6)

$F_{μ \max} = \frac{2 F_{nmax} μ_{p} R_{b}}{R_{t}}$ (7)

$F_{bmax} = \frac{Mg φ_{\max}}{2} \frac{b + φ_{\max} H_{g}}{L_{0}}$ (8)

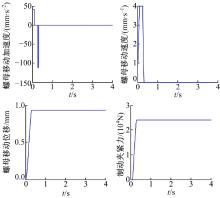
式中:F_{μ max}为单个制动器产生的最大制动力; $α_{n}$ 为安全系数; F_bmax为单个前轮产生的最大地面制动力; F_nmax为执行器能产生的最大制动夹紧力; μ _p为制动块摩擦系数; R_b为制动盘有效半径; R_t为车轮滚动半径; M为整车满载质量; g为重力加速度, 9.8 m/s²; $φ_{\max}$ 为地面峰值附着系数; b为满载时质心到后轴距离; H_g为满载时质心高度; L₀为轴距。

将式(6)(7)(8)联立得到F_nmax≥ 23515 N, 本文取F_nmax=24 000 N。为了满足制动力控制响应需求, 执行器应在0.3 s内产生最大制动夹紧力F_nmax, 同时需要在0.1 s内消除0.2 mm的制动间隙。

3.2 负载和运动规律需求约束

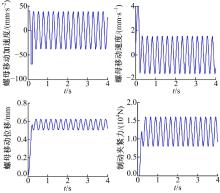
EMB执行器的负载及运动规律同时与制动夹紧力控制和整车制动力控制有关。本文针对紧急制动和高附着路面ABS两种工况, 分析执行器的负载和运动规律。参照Lee提出的以最大加速度工作到最大转速后匀速运动到制动间隙消除, 然后再减速到目标位置的时间最优控制算法^[5], 将滚珠丝杆螺母的移动速度线性简化, 结合系统等效刚度及执行器的目标性能得到图3所示的紧急制动工况下的负载和运动规律, 并由此获得执行器匹配的输入参数。根据文献[2]得到图4所示的高附着路面ABS工况下的负载规律和运动规律。

	Figure Option View Download New Window
	图3 紧急制动工况下负载和运动规律分析Fig.3 Load and motion law analysis for emergency braking

	Figure Option View Download New Window
	图4 ABS工况下负载和运动规律分析Fig.4 Load and motion law analysis for ABS braking

3.3 滚珠丝杆的约束

3.3.1 额定静载荷的约束

滚珠丝杆的额定静载荷C_a0应不小于轴向最大负载力, 即:

$C_{a 0} \geq α_{ca} F_{nmax}$ (9)

式中: $α_{ca}$ 为安全系数, 一般取为1~3, 本文取1。

3.3.2 额定动载荷的约束

备选滚珠丝杆应满足预期使用寿命的要求, 即:

$L_{h} = \frac{1 \times 10^{6}}{60 n_{sm}} {(\frac{C_{a}}{f_{load} F_{am}})}^{3} \geq L_{h}^{des}$ (10)

$n_{sm} = \frac{60}{2 π t_{d}} \int_{0}^{t_{d}} \frac{2 π}{l} \overset{\cdot}{x} (t) d t = 60 \frac{{\overset{\cdot}{x}}_{m}}{l}$ (11)

式中: $L_{h}$ 为在平均转速下的运行寿命, 单位为h; $n_{sm}$ 为平均转速, 单位为r· min^-1; $C_{a}$ 为滚珠丝杆的额定动载荷; $f_{load}$ 为与运行工况相关的负荷系数, 本文取值为1; $F_{am}$ 为平均负载; ${\overset{\cdot}{x}}_{m}$ 为平均移动速度; $L_{h}^{des}$ 为预期寿命, 本文取值为1000 h。

整理式(10)(11), 得到滚珠丝杆的额定动载荷应满足如下条件:

$C_{a} \geq f_{load} F_{am} \sqrt[3]{\frac{3600 L_{h}^{des} {\overset{\cdot}{x}}_{m}}{1 \times 10^{6} l}}$ (12)

3.3.3 临界转速的约束

当滚珠丝杆的转速大于滚珠丝杆轴的一阶弯曲固有频率 $ω_{c}$ 时将产生共振失稳的现象。因此, 滚珠丝杆的最大转速应满足如下条件:

$\frac{2 π}{l} {\overset{\cdot}{x}}_{\max} \leq α_{cs} ω_{c}$ (13)

式中: ${\overset{\cdot}{x}}_{\max}$ 为滚珠丝杆螺母的最大移动速度; $α_{cs}$ 为安全系数, 一般取值0.7~0.8, 本文取0.8。基于梁模型的假设, 滚珠丝杆轴的一阶弯曲固有频率为^[21]:

$\omega_{c}$=$\frac{\lambda}{L^{2}_{s}} \sqrt{\frac{E_{s}I_{s}}{A_{s}\rho}}$ (14)

式中: $λ$ 为与支撑方式相关的系数, 本文一端固定一端支撑的方式取值为15.4; $E_{s}$ 为滚珠丝杆轴的杨氏模量; $I_{s} = \frac{π}{64} d_{s 2}^{4}$ 为最小断面惯性矩, $d_{s 2}$ 为滚珠丝杆螺纹底径, $d_{s 2} = d_{s} - D_{ω}, d_{s}$ 为滚珠丝杆的公称直径, $D_{ω}$ 为滚珠直径, 本文取 $D_{ω} = 0.6 l; A_{s}$ 为滚珠丝杆轴的最小截面积, $A_{s} = \frac{π}{4} d_{s 2}^{2}; ρ_{s}$ 为滚珠丝杆轴的密度; $L_{s}$ 为滚珠丝杆长度。

整理式(13)(14), 得滚珠丝杆应满足:

$d_{s}\ge$$\frac{ 8\pi L^{2}_{s}\dot{x}_{max}\sqrt{\rho_{s}}}{\alpha_{c, s}\lambda l \sqrt{E_{s}}} +0.6L$ (15)

同时滚珠丝杆的转速应小于厂家提供的极限转速^[20], 即:

$\frac{2 π}{l} {\overset{\cdot}{x}}_{\max} \leq α_{D} \frac{2 π D_{N}}{60 d_{s}}$ (16)

$\begin{array}{l} 则 : d_{s} \leq \frac{α_{D} D_{N} l}{60 {\overset{\cdot}{x}}_{\max}} \end{array}$ (17)

式中: $α_{D}$ 为安全系数, 本文取0.8; $D_{N}$ 为循环单元的最大速率, 一般取值为0.6× 10⁵~2.2× 10⁵(mm· r)/min, 本文取值1.4× 10⁵ (mm· r)/min。

3.3.4 临界弯曲力约束

基于细长梁假设, 滚珠丝杆的轴向载荷应小于临界弯曲载荷, 否则将产生弯曲现象。因此, 滚珠丝杆应满足如下条件:

$F_{nmax} \leq α_{Euler} f_{Euler} \frac{E_{s} I_{s} π^{2}}{L_{s}^{2}}$ (18)

式中: $α_{Euler}$ 为安全系数, 本文取值为0.7; $f_{Euler}$ 为与支撑方式有关的系数, 本文取值为2。

由式(18)可知, 滚珠丝杆公称直径应满足:

$d_{s} \geq \sqrt[4]{\frac{64 F_{nmax} L_{s}^{2}}{f_{Euler} α_{Euler} E_{s} π^{3}}} + 0.6 l$ (19)

3.3.5 最大导程

增大滚珠丝杆的导程通常会降低位置精度, 为了满足位置精度要求, 滚珠丝杆的导程应满足:

$l \leq \frac{2 π δ x_{des}}{δ θ_{s}}$ (20)

式中: $δ x_{des}$ 为需求位置精度, 本文取值为0.001 mm; $δ θ_{s}$ 为传感器的精度, 本文取值为10'。

3.3.6 推力轴承的约束

由图1可知, 滚珠丝杆轴的公称直径应不小于推力轴承的最小安装尺寸, 即:

$d_{s} \geq d_{bamin}$ (21)

式中: $d_{bamin}$ 为最小推力轴承的内圈安装直径, 根据轴向载荷和推力轴承产品数据, 取值为21 mm。

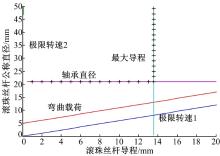
结合式(15)~(21), 得到导程和公称直径的可行域(如图5所示的“ +” 链接包围的区域, 即21≤ d_s≤ d_maxmm且l≤ 13.57 mm)。由式(17)确定的临界转速2约束下的最大公称直径 $d_{\max}$ 均为1e3量级。在数据库中选出导程和公称直径在此可行域内的滚珠丝杆。然后, 选择额定静载荷和额定动载荷满足式(9)(12)的滚珠丝杆。同时, 为降低系统转动惯量和结构尺寸, 在满足约束条件的前提下, 对于导程相同的滚珠丝杆应选择公称直径最小的。

	Figure Option View Download New Window
	图5 滚珠丝杆导程和公称直径的可行域Fig.5 Feasible domains of lead and diameter of ball screw

3.4 力矩电机运行范围的约束

3.4.1 电机等效连续输出力矩的约束

为了预防电机过热, 电机等效连续输出力矩 T_meq应小于电机的连续堵转力矩T_c, 即:

$T_{meq} \leq α_{mc} T_{c}$ (22)

式中: $α_{mc}$ 为安全系数, 本文取值为0.8。

如图3所示, 电机主要工作在堵转工况, 电机等效连续输出力矩为电机堵转时最大负载力矩, 即:

$T_{meq} = \frac{1}{r η_{g} η_{s}} F_{nmax}$ (23)

如图4所示, 动态负载作用下的电机等效连续输出力矩为电机负载力矩的均方根值T_mRMS, 即:

$T_{meq}=T_{mRMS}=\sqrt{\frac{1}{\tau}}\int_{0}^{\tau}(t)^{2}dt$ (24)

$\begin{array}{l} T_{mRMS}^{2} = {(J_{me} r {\overset{\cdot \cdot}{x}}_{RMS})}^{2} + {(\frac{1}{r η_{g} η_{s}} F_{nRMS})}^{2} + \\ \frac{2 J_{me}}{η_{g} η_{s}} {(\overset{\cdot \cdot}{x} F_{n})}_{mean} \end{array}$ (25)

式中: ${\overset{\cdot \cdot}{x}}_{RMS}$ 为螺母移动加速度的均方根值; F_nRMS为负载的均方根值; ${(\overset{\cdot \cdot}{x} F_{n})}_{mean}$ 为 $\overset{\cdot \cdot}{x} F_{n}$ 的等效值。

3.4.2 电机峰值输出力矩的约束

电机的峰值负载力矩T_mmax应不大于电机的峰值堵转力矩T_p, 即:

$T_{mmax} = \max |T_{m} (t)| \leq α_{mp} T_{p}$ (26)

式中:α _mp为安全系数, 本文取值为0.8。

3.4.3 电机峰值输出转速的约束

电机的负载峰值转速ω _mmax应不大于电机峰值转速ω _p, 即:

$ω_{mmax} = \frac{30 r}{π} {\overset{\cdot}{x}}_{\max} \leq α_{mω} ω_{p}$ (27)

式中:α _mω为安全系数, 本文取值为0.9。

3.4.4 电机性能约束下的系统传动比范围

结合式(23)和(27)所示的连续堵转力矩和峰值转速约束得到系统总传递比应满足式(28)和(29), 对于不满足式(29)的电机可直接排除。

$r \geq \frac{F_{nmax}}{η_{g} η_{s} α_{mc} T_{c}} 且 r \leq \frac{π α_{mω} ω_{p}}{30 {\overset{\cdot}{x}}_{\max}}$ (28)

$\begin{array}{l} \frac{F_{nmax}}{η_{g} η_{s} α_{mc} T_{c}} \leq \frac{π α_{mω} ω_{p}}{30 {\overset{\cdot}{x}}_{\max}} \end{array}$ (29)

3.4.5 力矩电机安装尺寸的约束

力矩电机的外径应满足:

$d_{mo} < \min (H, B)$ (30)

式中: $d_{mo}$ 为力矩电机的外径。

3.5 行星齿轮性能的约束

3.5.1 尺寸约束及约束下的最大传动比

由图1可知齿圈外径和太阳轮内径应满足:

$d_{rim} = 2 r_{r} + 3.5 \times 2.25 m < \min (H, B)$ (31)

$\begin{array}{l} d_{sb} = 2 r_{r} - 3.5 \times 2.25 m > d_{bmin} \end{array}$ (32)

式中: $d_{rim}$ 为齿圈外径; $r_{r}$ 为齿圈半径; m为齿轮模数; $d_{sb}$ 为太阳轮内径; $d_{bmin}$ 为最小推力轴承的公称直径。

如图1所示, 执行器中选择2Z-X(A)型行星齿轮传动, 此时行星齿轮的齿圈固定, 太阳轮为输入端, 行星架为输出端, 此时行星齿轮的传动比i_g为:

$i_{g} = 1 + \frac{r_{r}}{r_{sun}}$ (33)

式中: $r_{sun}$ 为太阳轮半径。

联立式(31)~(33)得到行星齿轮的最大传动比应满足如下条件:

$i_{g} < \frac{\min (H, B) - 3.5 \times 2.25 m}{d_{bmin} + 3.5 \times 2.25 m} + 1$ (34)

3.5.2 电机运行范围约束下的传动比范围

根据电机连续堵转力矩、电机峰值转速以及峰值转矩的限制, 得到不同电机和滚珠丝杆导程组合下的行星齿轮传动比应满足式(35)。

$i_{g} \geq \frac{l F_{nmax}}{2 π η_{g} η_{s} α_{mc} T_{c}} 且 i_{g} \leq \frac{l α_{mω} ω_{p}}{60 {\overset{\cdot}{x}}_{\max}}$ (35)

3.5.3 太阳轮最小齿数的约束

齿面接触强度应满足^[23]:

(36)

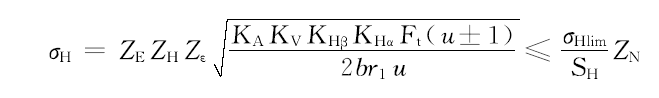
式中: $Z_{E}$ 为弹性系数; $Z_{H}$ 为节点区域系数; $Z_{ε}$ 为重合度系数, 由重合度确定; $K_{A}$ 为使用系数; $K_{V}$ 为动载系数; $K_{Hβ}$ 为齿向载荷分布系数; $K_{H} α$ 为齿间载荷分配系数; $F_{t}$ 为齿轮圆周力; $u$ 为齿数比, 本文太阳轮和行星齿轮间的齿数比 $u = (i_{g} - 2) / 2; b$ 为小齿轮齿宽; $r_{1}$ 为小齿轮半径; $σ_{Hlim}$ 为接触疲劳极限应力; $S_{H}$ 为接触强度最小安全系数; $Z_{N}$ 为接触强度寿命系数。

齿根弯曲疲劳强度应满足如下条件^[23]:

$σ_{F} = \frac{Y_{Fa} Y_{Sa} Y_{ε} K_{A} K_{V} K_{Fβ} K_{Fα} F_{t}}{bm} \leq \frac{σ_{Flim}}{S_{F}} Y_{N} Y_{X}$ (37)

式中:Y_Fa齿形系数; Y_sa为应力修正系数; $Y_{ε}$ 为重合度系数; K_Fβ齿向载荷分布系数; $K_{Fα}$ 为齿间载荷分配系数; m为齿轮模数; $σ_{Flim}$ 为弯曲疲劳极限应力; S_F为齿根弯曲强度最小安全系数; Y_N为弯曲强度寿命系数; Y_X为尺寸系数。

忽略摩擦损失, 太阳轮和行星齿轮间的圆周力为:

$F_{t} = \frac{l F_{nmax}}{6 π η_{s} η_{g} r_{sun} i_{g}}$ (38)

将式(36)~(38)联立, 可推导太阳轮的半径应满足如下条件:

(39)

4 目标函数

4.1 系统总质量

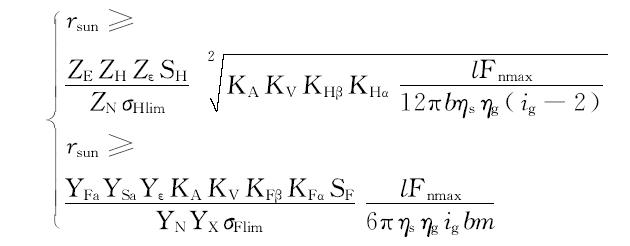
EMB执行器的质量为汽车簧下质量, 直接影响着汽车的行驶舒适性, 因此在匹配设计时应使其最小化。电机、行星齿轮组和滚珠丝杆的质量之和为:

$m = m_{m} + m_{g} + m_{s} + m_{n}$ (40)

式中:m为系统总质量; m_m为电机质量; m_g为行星齿轮组的质量; m_s为滚珠丝杆轴的质量。

4.2 系统启动加速度

执行器的系统启动加速度间接反映执行器的速度和位置响应速度, 影响制动夹紧力控制的响应时间, 因此在应使其最大化。系统启动加速度为:

$a = \frac{T_{p}}{r J_{me}} = \frac{T_{p}}{r (J_{m} + J_{g} + \frac{J_{s}}{{i_{g}}^{2}}) + \frac{1}{r} m_{n}}$ (41)

忽略J_g和J_s的影响, 无约束条件下的最大启动加速度为$a_{max}=\frac{T_{p}}{2\sqrt{m_{n}J_{m}}}$此时$r_{opta}=\sqrt{\frac{m_{n}}{J_{m}}}$, 满足文献[13]中的惯量匹配结果。

4.3 制动间隙消除时间

制动间隙消除时间为执行器制动夹紧力控制响应时间的一部分, 因此在匹配设计时应使其最小化。按照时间最优控制算, 以最大加速度工作到最大转速后匀速运动到制动间隙消除然后再减速到目标位置。制动间隙消除的时间为:

$t_{ag} = \frac{120 π x_{ag} r}{ω_{p}} + \frac{π ω_{p} (J_{m} + J_{g} + \frac{J_{s}}{{i_{g}}^{2}} + \frac{1}{r^{2}} m_{n})}{60 T_{p}}$ (42)

忽略 $J_{g}$ 和 $J_{s}$ 的影响, 当 $r_{optt} = \frac{1}{60} \sqrt[3]{\frac{m_{n} {ω_{p}}^{2}}{π T_{p} x_{ag}}}$ 制动间隙消除时间最短, 与文献[13]中的结果相符。

4.4 ABS工况电机等效连续输出力矩

电机等效连续输出力矩直接反应执行器制动过程中电机产生的能量消耗。如图4所示, ABS工况下的电机等效连续输出力矩应满足式(24)(25)。若忽略 $J_{g}$ 和 $J_{s}$ 的影响, $T_{m, RMS}^{2}$ 为 $r$ 的凸函数, 且使 $T_{m, RMS}$ 最小的无约束最优整体传动比 $r_{optT}$ 应满足: $\frac{\partial T_{me, RMS}^{2} (r)}{\partial r} = 0,$ 即, $r_{optT}=\sqrt{\lgroup \frac{1}{\eta_{g}\eta_{s}}F_{cl, RMS}+m_{n}\ddot{x}_{RMS} \rgroup/J_{m}\ddot{x}_{RMS}}$。在 $F_{cl} (t) = 0$ 的纯惯性载荷下, 使电机等效连续输出力矩最小的系统传递比和使启动加速度最大的系统传递比相同。

4.5 多目标函数

在对EMB执行器进行最优匹配时需要:使执行器的质量最小, 以减小汽车簧下质量; 使启动加速度最大, 使制动间隙消除时间最小, 以提高执行器对制动夹紧力控制的响应速度; 同时, 使电机等效连续输出力矩最小, 以降低制动过程中电机输出能耗。但是, 通常上述目标之间相互制约, 需要建立合适的多目标函数, 以实现执行器综合性能的最优化。本文拟以系统质量最小为首要优化目标、制动间隙消除时间次之、兼顾启动加速度和电机输出力矩, 建立多目标函数, 如式(43)所示:

$O = w_{1} \frac{m}{m_{\min}} + w_{2} \frac{a_{\max}}{a} + w_{3} \frac{t_{ag}}{t_{agmin}} + w_{4} \frac{T_{mRMS}}{T_{mRMSmin}}$ (43)

式中: $w_{1 ~ 4}$ 为多目标函数的权重因子, $w_{i} = w_{1 i} w_{2 i}; w_{1 i}$ 为设计者根据执行器的各目标的重要性来定义的权重因子(本文 $w_{11} = 0.7, w_{12} = 0.05, w_{13} = 0.15, w_{14} = 0.1); w_{2 i}$ 为用于调整各分目标在量级差方面影响的校正权重因子, 本文取各分目标函数值的梯度均方值的倒数; $m_{\min}$ 为最小系统质量; $a_{\max}$ 为最大启动加速度; $t_{agmin}$ 为最短制动间隙消除时间; $T_{mRMSmin}$ 为最小电机等效连续输出力矩。

5 匹配设计结果

5.1 备选滚珠丝杆的确定

在产品数据库^[24]中选出导程和公称直径在图5所示的可行域内的滚珠丝杆, 根据额定静载荷和额定动载荷进一步筛选备选滚珠丝杆。最后在满足所有约束条件的前提下, 对于导程相同的滚珠丝杆选择公称直径最小的, 得到表2所示的备选滚珠丝杆。

表2 备选滚珠丝杆的参数 Table 2 Parameters of candidate ball screw

序列	$l$ /mm	d_s /mm	C_a0 /kN	C_a /kN	m_n /kg	J_s /(10^-5 mm)
1	2.5	25	9	29.5	0.69	2.41
2	4	32	15	46.5	0.85	6.48
3	5	32	18.1	52.4	0.85	6.48
4	6	32	20.2	53.5	0.85	6.48
5	8	32	26.4	64.8	0.85	6.48
6	10	32	32	73	0.94	6.48

表2 备选滚珠丝杆的参数 Table 2 Parameters of candidate ball screw

5.2 备选电机的确定

首先在产品数据库^[24]中筛选出电机外径满足式(30)的所有电机; 将最大制动夹紧力、最大移动速度以及最大加速度等负载特征参数代入式(29)筛选备选电机; 然后根据式(34)确定在执行器尺寸限制下的最大行星齿轮传动比, 结合行星齿轮配齿数据库^[21], 确定备选行星齿轮的名义传动比i_g=[2.8, 3.15, 3.55, 4, 4.5, 5, 5.6, 7.1, 8](计算时齿轮模数m=1.25); 最后, 以行星齿轮的名义传动比、备选滚珠丝杆的导程及负载特征参数为输入结合式(22)~(27)确定电机的工作范围, 从而进一步确定满足条件的所有备选电机(见表3)。

表3 备选力矩电机的参数 Table 3 Parameters of candidate motor

型号	$T_{p}$ /(N· m)	$T_{c}$ /(N· m)	$ω_{p}$ /(r· min^-1)	$m_{m}$ /kg	$J_{m}$ /(kg· m²)
J110LYX023	6.2	3	1550	3.83	1.1× 10^-3
J130LYX04D	13	4.5	295	2.55	3.5× 10^-3
J92LYX11	14	5	300	5.29	2.2× 10^-4
J130LYX06A	24	6	330	4.15	1.5× 10^-2
J110LYX06	18	9	250	3.6	2.1× 10^-2

表3 备选力矩电机的参数 Table 3 Parameters of candidate motor

5.3 备选行星齿轮的设计

首先以最大制动夹紧力、备选滚珠丝杆导程及行星齿轮名义传动比为输入, 得到满足式(36)(39)的太阳轮最少齿数(本文齿轮材料为40 Cr, 齿宽 $b = 0.4 r_{sun}$ ); 然后以太阳轮最小齿数和名义传动比为输入, 在行星齿轮数据库^[22]中选出与备选滚珠丝杆导程相匹配的传动比和太阳轮齿数; 最后根据式(34)描述的传动比范围及式(39)所示的齿轮强度需求, 进一步确定与电机和滚珠丝杆导程相匹配的行星齿轮实际传动比和太阳轮齿数, 即得到满足条件的所有匹配方案(见表4)。

表4 EMB执行器的可行匹配方案 Table 4 Feasible selection results of EMB actuator

电机型号	$l$ /mm	i_g	齿数 Z_s	m_tot /kg	$a$ /(mm· s^-2)	t_xag /s	T_{m, RMS} /(N· m)
J110LYX023	2.5	5.1	20	5.13	434.58	0.030	0.99
J110LYX023	2.5	5.7	20	5.22	387.48	0.032	0.86
J92LYX11	2.5	2.8125	32	6.58	7841.19	0.045	1.94
J92LYX11	2.5	3.12	25	6.46	7657.76	0.050	1.75
J92LYX11	4	4.4348	23	6.96	8366.81	0.045	1.97
J92LYX11	5	5.7	20	7.03	8205.25	0.046	1.92
J130LYX06A	2.5	2.8125	32	5.44	225.86	0.052	1.17
J130LYX06A	2.5	3.12	25	5.32	203.87	0.056	0.80
J130LYX06A	4	3.9	20	5.65	261.00	0.046	1.62
J130LYX06A	4	4.4348	23	5.82	229.37	0.051	1.21
J130LYX06A	4	5.1	20	5.80	199.53	0.057	0.72
J130LYX06A	5	5.1	20	5.80	249.41	0.048	1.48
J130LYX06A	5	5.7	20	5.89	223.10	0.052	1.12
J130LYX06A	6	5.7	20	5.89	267.73	0.045	1.70
J110LYX06	4	2.8125	32	5.24	193.67	0.049	2.52
J110LYX06	4	3.12	25	5.12	174.75	0.053	2.12
J110LYX06	5	3.1034	29	5.22	219.49	0.045	3.02
J110LYX06	4	3.5455	22	5.11	153.81	0.058	1.65
J110LYX06	5	3.52	25	5.18	193.60	0.049	2.51
J110LYX06	4	3.9	20	5.10	139.85	0.062	1.28
J110LYX06	5	4.0909	22	5.18	166.62	0.055	1.95
J110LYX06	6	3.913	23	5.19	209.01	0.047	2.82
J110LYX06	5	4.4348	23	5.27	153.66	0.058	1.64
J110LYX06	6	4.4348	23	5.27	184.39	0.051	2.33
J110LYX06	5	5.1	20	5.25	133.65	0.064	1.10
J110LYX06	6	5.1	20	5.25	160.38	0.056	1.80
J110LYX06	8	4.9565	23	5.37	219.92	0.045	3.03
J110LYX06	6	5.7	20	5.34	143.47	0.061	1.38
J110LYX06	8	5.7272	22	5.48	190.30	0.050	2.45

表4 EMB执行器的可行匹配方案 Table 4 Feasible selection results of EMB actuator

5.4 各目标下的最优选择

分析表4中的所有匹配方案可知:①以系统质量最小为目标的最优匹配方案为:J110LYX06电机+导程为4的滚珠杆+传动比为3.9(太阳轮齿数为20)的行星齿轮, 其质量为5.1 kg; ②以系统启动加速度最大为目标的最优匹配方案为:J92LYX11电机+导程为4的滚珠丝杆+传动比为4.4348(太阳轮齿数为23)的行星齿轮; ③以制动间隙消除时间最短为目标的最优匹配方案为:J110LYX023电机+导程为2.5的滚珠丝杆+传动比为5.1(太阳轮齿数为20)的行星齿轮; ④以ABS工况下的电机等效连续输出力矩最小为目标的最优匹配方案为:J130LYX06A电机+导程为4的滚珠丝杆+传动比为5.1(太阳轮齿数为20)的行星齿轮。将上述不同目标下的最优匹配结果代入式(43), 可获得多目标优化的匹配方案, 其匹配方案与制动间隙消除时间最短的匹配方案相同。分析该匹配方案可知:系统质量为5.13 kg, 与最小系统质量相比仅增加了0.6%; 启动加速度为434.58 mm· s^-2, 仅小于包含J92LYX11电机的匹配方案; 制动间隙消除时间为0.03 s, 为最短制动间隙消除时间; 电机等效连续输出力矩为0.99 N· m, 与最小电机等效连续输出力矩相比仅增加了0.27 N· m; 该方案实现了执行器综合性能的最优化(见表5)。

表5 不同目标下的最优匹配结果 Table 5 Results of different optimization criteria

最优目标	电机型号	丝杆导程 $l$	传动比 i_g
质量最小	J110LYX06	4	3.9
启动加速度最大	J92LYX11	4	4.4348
制动间隙消除时间最短	J110LYX023	2.5	5.1
力矩电机等效输出力矩最小	J130LYX06A	4	5.1
多目标函数最小	J110LYX023	2.5	5.1

表5 不同目标下的最优匹配结果 Table 5 Results of different optimization criteria

6 结论

(1)基于执行器的动力学模型和性能目标提出合理的负载特征和运动规律是匹配设计的前提。

(2)将弯曲载荷、极限转速、使用寿命、位置精度等滚珠丝杆的性能需求及尺寸限制等约束条件通过图形描述为滚珠丝杆导程和公称直径的可行域, 直观地表达了各约束条件间的矛盾。

(3)以电机产品数据库和备选滚珠丝杆导程为输入, 结合由尺寸限制确定的行星齿轮传动比范围决定了电机的运行范围, 进而确定了备选电机。

(4)以备选滚珠丝杆和电机为输入, 以太阳轮尺寸最小为目标, 以齿面接触强度和齿根弯曲强度为约束条件, 获得了能够驱动负载的行星齿轮的传动比和太阳轮齿数, 进而找到了所有满足条件的匹配方案。

(5)分析了各匹配方案的系统质量、启动加速度、制动间隙消除时间及电机输出力矩, 获得了不同目标下的最优匹配结果, 并实现了多目标优化。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Ahn J K, Jung K H, Kim D H, et al. Analysis of a regenerative braking system for hybrid electric vehicle using an electro-mechanical brake[J]. International Journal of Automotive Technology, 2009, 10(2): 229-234. [本文引用:1]
[2]	Line C. Modelling and control of an automotive electromechanical brake[D]. Melbourne: The University of Melbourne, 2007. [本文引用:2]
[3]	Schwarz R, Isermann R, Böhm J, et al. Clamping force estimation for a brake-by-wire actuator[C]∥SAE Paper, 1999-01-0482. [本文引用:2]
[4]	Kwak J, Yao B, Bajaj A. Analytical model development and model reduction for electromechanical brake system[C]∥ASME Internetional Mechanical Engineering Congress and Exposition, Anaheim, United States, 2004. [本文引用:3]
[5]	Lee C F, Manzie C. High-band width clamp force control for an electromechanical brake[C]∥SAE Paper, 2012-01-1799. [本文引用:2]
[6]	李静, 张建, 王梦春, 等. 电子机械制动执行器数学建模与精细控制[J]. 吉林大学学报: 工学版, 2012, 42(1): 1-6. Li Jing, Zhang Jian, Wang Meng-chun, et al. Electromechanical brake actuator modeling and actuator control algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(1): 1-6. [本文引用:1]
[7]	Hilzinger J, Schumann F, Blosch G, et al. Electromechanical wheel brake device[P]. United States Patent: US 6806602 B2, 2014-10-19. [本文引用:1]
[8]	Schwarz R. Electromechanically actuated disc brake[P]. United States Patent: US 6315092 B1, 2001. [本文引用:1]
[9]	Osterday C A, Fiste M M, Hill G J. Electrically actuated disc brake assembly[P]. United States Patent: US 6315092 B1, 2001-11-13. [本文引用:1]
[10]	Wang N, Kaganov A, Code S, et al. Actuating mechanism and brake assembly[P]. PBR Australia Pty: WO2005/124180 A1, 2005-12-29. [本文引用:2]
[11]	杨坤. 轻型汽车电子机械制动及稳定性控制系统研究[D]. 长春: 吉林大学汽车工程学院, 2009. Yang Kun. Research of electromechanical brake and vehicle stability control system for light vehicle[D]. Changchun: College of Automotive Engineering, Jilin University, 2009. [本文引用:1]
[12]	赵一博. 电子机械制动系统执行机构的研究与开发[D]. 北京: 清华大学机械工程学院, 2010. Zhao Yi-bo. Research and development of electromechanical brake system actuator[D]. Beijing: College of Mechanical Engineering, Tsinghua University, 2010. [本文引用:1]
[13]	Pasch K A, Seering W P. On the drive systems for high-performance machines[J]. Trans ASME, 1984, 106: 102-108. [本文引用:3]
[14]	Cusimano G. A procedure for a suitable selection of laws of motion and electric drive systems under inertial loads[J]. Mech Mach Theory, 2003, 38: 519-533. [本文引用:1]
[15]	Cusimano G. Generalization of a method for the selection of drive systems and transmissions under dynamic loads[J]. Mechanism and Machine Theory, 2005, 40(5): 530-558. [本文引用:1]
[16]	Giberti H, Cinquemani S, Legnani G. Effects of transmission mechanical characteristics on the choice of a motor-reducer[J]. Mechatronics, 2010, 20: 604-610. [本文引用:1]
[17]	Roos F, Johansson H, Wikand er J. Optimal selection of motor and gearhead in mechatronic application[J]. Mechatronics, 2006, 16: 63-72. [本文引用:1]
[18]	Kim M S, Chung S C. Integrated design methodology of a ball-screw driven servomechanisms with discrete controllers. Part I: modelling and performance analysis[J]. Mechatronics, 2006, 16: 491-502. [本文引用:1]
[19]	Kim M S, Chung S C. Integrated design methodology of a ball-screw driven servomechanisms with discrete controllers. Part II: formulation and synthesis of the integrated design[J]. Mechatronics, 2006, 16: 503-512. [本文引用:1]
[20]	Caracciolo R, Richiedei. D. Optimal design of ball-screw driven servomechanisms through an integrated mechatronic approach[J]. Mechatronics, 2014, 24: 819-832. [本文引用:2]
[21]	Dumitru D, Strajescu E, Tache C. Theoretical considerations concerning the determination of value for the critical speed of the ball-screws from numerical axes structure[J]. RECENT, 2009, 10(27): 255-258. [本文引用:2]
[22]	饶振纲. 行星齿轮传动设计[M]. 北京: 化学工业出版社, 2003. [本文引用:1]
[23]	龙振宇. 机械设计[M]. 北京: 机械工业出版社, 2002. [本文引用:2]
[24]	南京工艺装备制造有限公司. 产品数据库[DB/OL]. [2017-07-26]. http:∥www.njyigong.cn/products.asp?parentid=1 [本文引用:2]

2009

0.0

... 0 引言与传统液压制动系统相比,电子机械制动系统(Electro-mechanical brake, EMB)在制动力控制方面的诸多优势吸引了国内外研究人员及企业的重视^{[1,2,3,4,5,6]} ...

2007

0.0

... 根据文献[2]得到图4所示的高附着路面ABS工况下的负载规律和运动规律 ...

1999

0.0

... 忽略温度和磨损的影响,认为制动夹紧力F_n与制动块位移存在如下数学关系^[3,4]: ...

2004

0.0

... 忽略温度和磨损的影响,认为制动夹紧力F_n与制动块位移存在如下数学关系^[3,4]: ...

... 式中:K_b为系统等效刚度,根据文献[4]取值为3 ...

2012

0.0

... 参照Lee提出的以最大加速度工作到最大转速后匀速运动到制动间隙消除,然后再减速到目标位置的时间最优控制算法^[5],将滚珠丝杆螺母的移动速度线性简化,结合系统等效刚度及执行器的目标性能得到图3所示的紧急制动工况下的负载和运动规律,并由此获得执行器匹配的输入参数 ...

2012

0.0

. 2012, 42(1):1-6

Electromechanical brake actuator modeling and actuator control algorithm

电子机械制动执行器数学建模与精细控制

Li Jing , Zhang Jian , Wang Meng-chun

李静, 张建, 王梦春

2014

0.0

... Bosch^[7]、Continental Teves^[8]、Delphi^[9]和PBR^[10]等公司分别提出了EMB执行器的不同结构,其中驱动电机、齿轮减速器、将旋转运动转化为直线运动的运动转换机构是影响其性能的关键部件 ...

0.0

2001

0.0

2005

0.0

... 1 执行器的结构特征分析参照Wang设计的专利结构^[10]提出图1所示的行星齿轮滚珠丝杆驱动式EMB执行器的结构简图:分装式力矩电机的空心轴式转子和太阳轮固定链接,转子内安装滚珠丝杆及推力轴承,滚珠丝杆轴穿过太阳轮与行星架输出端链接 ...

2009

0.0

. 2009, :-

Research of electromechanical brake and vehicle stability control system for light vehicle

轻型汽车电子机械制动及稳定性控制系统研究

Yang Kun

杨坤

以某轻型汽车为研究对象,对基于汽车电子机械制动(Electromechanical Brake,EMB)的汽车稳定性控制系统(Vehicle Stability Control,VSC)进行研究。针对目标车型研制了四台EMB执行器及一套实用的电子制动踏板;提出了车轮EMB控制系统的结构及总体方案,并进行了软硬件设计。通过EMB执行器特性试验,得到了EMB执行器特性曲线并测得了EMB执行器建模所需参数,通过离线仿真和台架试验对EMB控制参数进行调节,并对其性能进行了验证。确定了基于EMB的VSC控制算法,自主研发了VSC控制器硬件,搭建了基于EMB的VSC离线仿真平台和硬件在环试验平台,对在EMB基础上集成VSC的可行性进行了验证。本文的研究为EMB系统设计及基于EMB的VSC的应用开发提供了重要参考。

... 杨坤^[11]和赵一博^[12]采用传统方法对EMB执行器进行了匹配设计,但由于执行器的尺寸限制、电机运行范围及行星齿轮和滚珠丝杆的性能需求等未能综合考虑,需要通过反复计算获得一种可行方案,且并非最优方案 ...

2010

0.0

. 2010, :-

Research and development of electromechanical brake system actuator

电子机械制动系统执行机构的研究与开发

Zhao Yi-bo

赵一博

电子机械制动(Electromechanical Brake,EMB)技术,作为汽车线控制动技术的一个分支,无论是在原理还是结构上都与传统汽车制动系统有很大的区别,是一种全新的汽车制动理念。EMB系统结构简单、性能优异、节能环保,拥有巨大的应用前景和市场价值。在国外,Bosch、Siemens、Continental Teves等公司针对EMB已经开展研究并已经取得了部分研究成果,而国内的研究仍处于起步阶段。执行机构作为EMB系统最重要的组成部分之一,是产生制动力的关键部件。本文围绕电子机械制动系统执行机构开展研究工作。在充分调研分析国内外EMB执行机构开发及研究成果的基础上,提出了一种独特的EMB执行机构结构方案。该方案由永磁直流力矩电机、行星齿轮减速器及滚珠丝杠机构组成,通过将行星齿轮减速器布置于分装式力矩电机的中空部分,使EMB执行机构整体轴向尺寸缩短,以适应轮边狭小空间的布置需要。以某轿车前轮盘式制动器为例,进行了EMB执行机构样机的设计开发。经校核计算,该样机产生的制动夹紧力可满足国内相关制动法规要求,机械强度满足要求。对EMB执行机构各部分的原理及工作特性进行理论推导,建立了包括电机、摩擦特性、传动机构、负载及制动器的数学模型,设计了EMB执行机构三闭环PID控制系统结构,并在Matlab/Simulink环境下建立了各部分对应的仿真模型。针对驱动电机特性及EMB执行机构控制开展仿真研究,验证了理论推导和仿真模型的正确性以及提出的EMB执行机构控制系统的合理性,分析了对EMB执行机构控制系统响应特性的要求,并在仿真过程中整定出了各环节控制参数。仿真结果表明:通过选取合适的控制参数,EMB控制系统性能满足设计要求。本文提出了EMB执行机构试验台方案,完成了机械、控制和测试部分的开发选型及试验台的安装、调试工作。利用该试验台,进行了EMB执行机构驱动电机性能试验研究以及负载特性试验。通过试验,得到了驱动电机相关工作特性曲线及参数。通过数据处理与分析验证了制动夹紧力与丝杠轴向位移的关系。通过本课题的研究,为EMB执行机构的设计及今后EMB控制器的开发积累了经验。

1984

0.0

... Pasch等^[13]以系统加速度最大和特定运动规律下运动时间最短为目标,提出纯惯性载荷下的电机和减速器的最优匹配方法 ...

... 忽略J_g和J_s的影响,无约束条件下的最大启动加速度为$a_{max}=\frac{T_{p}}{2\sqrt{m_{n}J_{m}}}$此时$r_{opta}=\sqrt{\frac{m_{n}}{J_{m}}}$,满足文献[13]中的惯量匹配结果 ...

... 忽略 Jg和 Js的影响,当 roptt=160mnωp2πTpxag3制动间隙消除时间最短,与文献[13]中的结果相符 ...

2003

0.0

... Cusimano^[14]研究了负载运动规律对以电机等效连续输出力矩最小为目标的最优匹配的影响 ...

2005

0.0

... 之后,Cusimano^[15]考虑了动态阻力载荷及减速器转动惯量的影响,以电机等效连续输出力矩最小为目标,应用迭代方法得到特定运动规律下的电机和减速器的最优匹配 ...

2010

0.0

... Giberti等^[16]考虑了齿轮的转动惯量和传动效率的影响,以电机的运行范围和齿轮机械特性为约束条件,以电机等效连续输出力矩最小为目标进行最优匹配,发现齿轮的转动惯量和传动效率对最优匹配结果有显著影响 ...

2006

0.0

... Roos等^[17]利用电机和齿轮的产品数据库,以电机运行范围和齿轮的性能要求为约束条件在数据库中选出能够驱动负载的电机和齿轮组合,并分别给出电机等效连续输出力矩、系统重量、峰值功率及系统能耗等最小化的匹配方案,但在匹配时未考虑齿轮转动惯量和传动效率的影响 ...

2006

0.0

... 关于电机与滚珠丝杆的最优匹配也有报道,Kim等^[18,19]以滚珠丝杆导程、公称直径、控制增益等为选择变量,以电机运行范围和滚珠丝杆弯曲载荷为约束条件,以电机需求功率和系统惯量最小为目标,实现了对滚珠丝杆驱动机电系统的多目标多约束下的整体最优匹配 ...

2006

0.0

2014

0.0

... Caracciolo^[20]不仅考虑了滚珠丝杆的性能需求和电机运行范围等约束条件,同时将惯量比和控制带宽等影响系统闭环控制特性的参数也转化为约束条件,实现了将多目标优化转化为以电机等效连续输出力矩最小为目标的单目标优化 ...

... 同时滚珠丝杆的转速应小于厂家提供的极限转速^[20],即: ...

2009

0.0

... 基于梁模型的假设,滚珠丝杆轴的一阶弯曲固有频率为^[21]: ...

... 然后根据式(34)确定在执行器尺寸限制下的最大行星齿轮传动比,结合行星齿轮配齿数据库^[21],确定备选行星齿轮的名义传动比i_g=[2 ...

2003

0.0

... 然后以太阳轮最小齿数和名义传动比为输入,在行星齿轮数据库^[22]中选出与备选滚珠丝杆导程相匹配的传动比和太阳轮齿数 ...

2002

0.0

... 齿面接触强度应满足^[23]: ...

... 齿根弯曲疲劳强度应满足如下条件^[23]: ...

0.0

. , :-

南京工艺装备制造有限公司

... 1 备选滚珠丝杆的确定在产品数据库^[24]中选出导程和公称直径在图5所示的可行域内的滚珠丝杆,根据额定静载荷和额定动载荷进一步筛选备选滚珠丝杆 ...