作者简介:刘翔宇(1991-),男,博士研究生.研究方向:智能交通运输系统.E-mail:liubeixiangyu@163.com
为提高可变信息板选址的精确度以及交通诱导的效益,从交通诱导的角度应用随机游走算法对交通诱导小区划分进行了研究。将城市路网以路段为节点映射为复杂网络图,在对网络进行分析的基础上,构建了网络图的拉普拉斯矩阵,并利用组合狄利克雷问题的求解方法对模型进行求解。以沈阳市某路网为实例,验证了模型的可行性。
In order to improve the accuracy of location selection of the variable information board and improve the benefit of traffic guidance, the urban road network is divided from the point of view of traffic induction using random walk algorithm. Based on the analysis of the network built by taking road section as node, the Laplacian matrix of the network graph is constructed. Then, the model is solved by the method of solving the combining Dirichlet problem. Taking Shenyang Road Network as an example, the feasibility of the proposed model is verified.
交通诱导是解决交通拥堵问题的有效手段, 是智能运输系统的重要组成部分。国内外学者在研究交通诱导时, 动、静态诱导的路径规划和可变信息板的选址方法等是主要研究问题。文献[1, 2]分别研究了云环境下的最短路径求解算法, 提出了城市整体路网下的最短路径求解模型。马旭辉[3]研究了网络控制子区动态划分方法, 以路口为节点, 相邻路口连接路段为边, 路段阻抗为边权值建立有向加权网络图和邻接矩阵, 利用网络顶点K步可达结构分解方法对网络进行了划分。Zhou等[4]利用宏观基本图对子区划分进行了研究, 通过分析宏观基本图, 以各区域的相似性为特性对小区进行划分, 将具有同质交通流的区域归为同一小区。Ji等[5]则将图像分割技术引入宏观基本图, 以路段密度值为特性对路网进行分区。郭佳宁[6]从交通诱导角度出发, 对城市路网的分区优化进行了研究。利用图论中的归一化分割准则对城市路网进行了分区, 分析城市路网的整体拓扑结构与城市结构的关系, 提出城市路网优化方法。由以上研究现状可知, 目前国内外学者对路网分区的研究大都集中在交通控制小区领域, 在交通诱导领域的研究多是动态路径规划和可变信息板的选址问题, 缺乏针对交通诱导小区划分的研究。
本文针对大范围路网下进行诱导路径规划和可变信息板选址时计算量过大的特点, 从交通诱导的角度出发, 利用随机游走算法对城市路网进行诱导小区划分。最后, 利用沈阳市部分路网数据, 验证了模型的可行性。
随机游走算法是一种常见于图像分割和图像识别等图像处理领域的交互式算法。该算法可用来处理离散目标, 也就是要求图论中图的节点和边必须是有限的[7]。随机游走算法在解决图论问题时, 涉及到边、节点、边权值以及度。
假定将所有节点划分为K个区域, 需选择K个节点作为种子点, 每个区域均有一个种子点, 计算随机游走者从每个非种子点的节点出发, 首次抵达所有种子点的概率, 得到每个非种子点的K个概率。再由概率最大准则, 认为每个非种子点与其对应概率最大的种子点处于同一区域。
随机游走者首次抵达一个种子点的概率与该种子点边值条件的Dirichlet问题具有相同的解[8, 9]。该种子点到达本身的概率为1, 其到达其他种子点的概率为0。而在图论中, 可通过电路图中节点的电势给出离散Dirichlet问题的解, 本文用边权值的倒数表示电阻, 取节点的电势为边值条件。
如图1(d)所示, L1、L2、L3为3个种子点, 随机游走者由非种子点首次游走到3个种子点的概率如图1(a)、(b)、(c)表示。如图1所示, 虚线圈内的非种子点首次到达3个种子点L1、L2、L3的概率分别为0.33、0.53、0.14, 概率之和为1。由概率最大原则, 将该非种子点与种子点L2划分入同一区域, 依此方法对其他非种子点逐一进行划分。
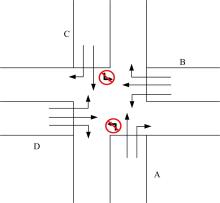
城市道路网络是一种特殊的有向网络, 将路网映射为网络图时有以下两种方法:①将交叉口作为节点进行映射; ②将路段作为节点进行映射。将交叉口作为节点进行映射时, 节点间的边权值表示两交叉口间的连接性, 常见于交通控制小区的划分。将路段作为节点时, 节点间的相邻性表示路段的连通性。在进行交通诱导小区划分时, 小区划分的目的是方便进行交通诱导的路径选择和可变信息板的选址, 考虑到路径因素需要将路段映射为节点。该方法可以很好地区分路段相连但路径不通的情况。如图2所示, 在禁左路口, 将路段A与路段D对应节点间的边权值定义为0, 则路段A与路段D在网络图中也不连通。
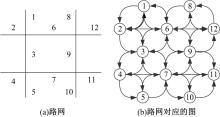
路网到网络图的映射形式如图3所示, 图3(a)中路段编号与图3(b)中节点的编号相同, 将路网转化为有向网络图。
在对诱导小区进行划分时诱导小区的大小以及划分后在诱导小区内发布诱导信息, 均需考虑路段之间的时空相关性。因此, 选取基本路段时空相关系数作为网络图中的边权值, 并对其进行分析。
(1)时间相关性
路段之间的时间相关性主要通过车流随时间在路段上流动体现, 车流的变动导致路网内各路段流量的变化。因此, 本文采用两路段之间交通量的相关性来表述路段之间的时间相关性。
两个变量之间的相关性通常采用皮尔逊相关系数来度量。路段i与路段j之间的相关系数如下所示:
式中:E(* )为参数的期望; D(* )为表示参数的方差ρ ij为路段i与路段j之间的相关系数; fi、fj分别为路段i与路段j间的流量。
(2)空间相关性
路段之间的空间相关性主要通过两路段之间的最短距离体现, 路段之间最短距离越短, 则相关性越高。本文利用高斯模糊集合定义了路段之间的空间相关系数:
式中:tij为路段i与路段j之间最短路径的长度。
本文将路段之间的时空相关系数用时间相关系数与空间相关系数的乘积表示[10]:
诱导小区划分区别于常见的控制小区划分, 在进行控制小区划分时需要根据交通量的变化适时调整, 目前主要考虑时效性对控制小区的划分进行研究, 主要研究交通控制子区动态划分方法。而诱导小区划分主要是为方便对诱导装置进行选址布设, 诱导装置布设后较长的一段时间内不会变更, 所以诱导小区划分后无需进行实时调整。在对诱导小区进行划分时, 需要根据历史拥堵情况, 选择拥堵严重的路段作为关键路段, 根据路段间的相关性进行聚类, 得到小区划分结果。该方法属于交互式方法, 可以很好地与随机游走算法相结合, 所以本文利用随机游走算法对行诱导小区进划分, 流程图如图4所示。
基于随机游走算法的诱导子区划分方法流程如下:
Step1 根据研究区域的大小确定诱导子区数量K, 根据路网内路段的拥挤程度选择K个关键路段作为种子点, 如图5(a)所示。用Vm表示K个种子点的集合。
Step2 随机游走算法模型
以路段为节点、路段间的时空相关系数为边权值将路网映射为复杂网络图, 如图5(b)所示。求解网络图的拉普拉斯矩阵, 矩阵中每个元素的值如下式所示:
式中:wij为节点i和j间的边权值; di为节点i的度, 在复杂网络中节点的度又分入度和出度, 节点的度可用来反映该节点在网络中的重要程度, 节点的度越大其在网络中的重要程度越高。本文在进行诱导子区划分时主要考虑路段间的相互联系, 参考基于复杂网络的城市交通演化理论[11], 将节点的度定义为出度与入度之和。
为便于计算, 将整个路网V分成两部分, K个关键路段组成一部分, 为K个种子点的集合Vm, 剩余的其他路段组成另一部分, 为非种子点的集合Vu, Vm∪ Vm=V, Vm∩ Vu=⌀, 则该网络图的拉普拉斯矩阵如下式所示:
式中:
设$x^{s}_{i}$表示非种子点vi首次抵达种子点s的概率, 定义种子点的归属函数Q(vj)=S, ∀vj∈Vm, 0< S≤K, 令
则对每个种子点 , 组合Dirichlet问题可由下式求解:
式(7)中需要满足
Step3 将网络图的划分结果还原至路网, 得到路网的划分初次结果, 如图5(d)所示。
Step4 利用道路、铁路、河流等人工或天然屏障对子区边界进行调整。
Step5 利用诱导子区的特性阈值对划分结果进行判断, 若满足阈值, 则算法结束; 若不满足阈值, 则返回Step1。
交通诱导小区划分的主要目的是便于交通诱导, 交通诱导可以缓解城市交通拥挤、提高居民出行效率。本文选取小区饱和度(表示诱导小区内流量分布)、道路拥挤率(表示诱导小区内道路的拥挤程度)和用来限制诱导小区范围的路网规模作为诱导小区划分时的特性参数。
(1)小区饱和度
在进行小区划分时, 为表示整个小区内的交通流特性, 无法用传统的道路饱和度表示, 本文用小区饱和度对小区内路网的交通流状态进行表示。小区饱和度为小区内交通需求总量与路网总通行能力的比值, 如下所示:
式中:V为道路网的交通需求量; C为道路网的通行能力; L有效为路网内道路的有效长度; D为诱导小区内的交通需求; T为有效服务时间, 本文选取高峰小时的3600 s; lp为机动车平均出行距离; Cap为路网容量; α 为路网折减系数。小区饱和度反映了诱导小区内交通流的空间优化程度。当饱和度低于0.5时, 诱导小区内交通需求量较少, 此时诱导小区内的交通效益较低。当诱导小区饱和度高于0.8时, 路网即将达到饱和状态, 行驶中的车辆会对整个车流产生随机干扰, 交通流的随机扰动会导致小区饱和度的浮动。当浮动导致饱和度大于0.9时, 车辆将对路段的平稳行驶产生更大干扰, 随之导致小区内道路网络的可靠性下降。因此, 本文在进行诱导小区划分时选取小区饱和度的范围为0.5~0.8[6]。
(2)道路拥挤率
小区饱和度虽然反映了诱导小区内交通流的总体状态, 但是由于居民出行热点区域的分布不均衡, 使路网内流量分布并不均衡, 每条路段的饱和度不同。同一饱和度的诱导小区, 其交通流可能处于均衡状态或部分拥挤部分自由流状态。为反映诱导小区内路段的交通拥挤情况, 定义道路拥挤率如下式所示:
式中:lcr为诱导小区内所有拥挤路段长度; L为诱导小区内路网总长度。
当道路拥挤率较小时, 多数路段处于自由流状态, 驾驶员可以忽略诱导信息随机选择出行路径, 出行时间基本不受影响, 此时诱导装置几乎不起作用, 诱导效率较低。当道路拥挤率过高时, 无有效诱导路径供驾驶员选择, 诱导装置无法对拥挤区域进行分流。根据以往的研究, 本文在进行诱导小区划分时选取道路拥挤率的范围为0.1~0.5[6]。
(3)路网规模的限制
诱导装置所发布诱导信息的影响范围是有限的, 当路段距离诱导装置所在路段较远时, 诱导装置所发布的诱导信息将失去时效性。为保证诱导装置发布信息的效益性, 需确保诱导小区的路网范围不超过某一限定值。本文根据路段之间的空间相关性确定诱导小区内路网范围的最大值。
由路段间的空间相关系数
在选取验证区域时, 需结合驾驶员的识认性和诱导效果选取路网大小。路网过大将导致诱导信息加速衰减从而使诱导效果降低; 路网过小导致诱导小区内可替代路径少, 无法进行诱导分流, 同时由于路段间相关性偏大, 无法进行诱导小区的划分。再者验证区域较小时, 区域内的路段也相对较少, 会增加验证实验的偶然性, 导致模型的可信度下降; 若验证区域过大会增加模型的运行时间, 降低模型验证的效率。因10~20个交叉口已初具小型路网的功能, 既可进行交通诱导, 又可保证模型的效率, 所以在进行验证时每个诱导小区内的交叉口个数选为10~20个。在对路网进行诱导小区划分时, 划分出3~4个小区即可对模型实现验证, 故选取包含40~80个交叉口的路网作为验证区域。
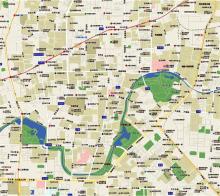
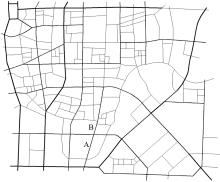
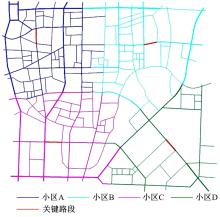
本文在沈阳市选取部分区域进行模型验证, 验证区域南起文化路北至市府大路, 东起万柳塘路西至青年大街。图6为所选的验证区域, 图7为将验证区域简化后的路网图。将验证区域内的路网映射为有向网络图, 图8为路网左上角部分的映射对应关系图。
根据验证区域的大小和城市基本功能分区, 将验证区域划分为4个诱导小区。根据历史拥堵数据, 选取奉天街在望云寺路与中山路之间的路段、大东路在银元街与小么什街之间的路段、文艺路在小南街与风雨坛街之间的路段、长青街在泉园二路与泉园一路之间的路段为关键路段, 并将其作为随机游走算法模型中的种子点。
将验证区域内路段的流量与长度代入式(3), 求得路段之间的时空相关系数。以图7中两相邻的路段A、B为例, 简述时空相关系数的计算过程, 路段A、B间的距离tAB=0.8 km, 路段A、B在高峰小时内每10 min的流量VA、VB见表1。
| 表1 A、B路段十分钟流量 Table 1 A、B road traffic flow for 10 min |
将表1数据代入式(1)求得路段A、B间的时间相关系数为ρ AB=0.418, 代入式(2)求得段A、B间的空间相关系数dAB=0.987, 再由式(3)求得时空相关系数rAB=0.524。
将验证区域的路网转为有向网络图, 求得有向网络图的邻接矩阵。计算节点的度, 并将所有节点分为种子点Vm={26, 120, 256, 398}和非种子点Vu, 由式(5)求得网络图的拉普拉斯矩阵, 表2为部分拉普拉斯矩阵。
| 表2 部分拉普拉斯矩阵 Table 2 Part of Laplacian matrix |
利用式(6)(7)进行求解, 得到节点j的
由图9可知, 浑河的一个分支穿过研究区域, 同时热闹路和朝阳街等主干路处于诱导小区边界区域, 因此需要对诱导小区边界进行调整。将朝阳街作为诱导子区A、B的边界, 并将其归入子区B。将热闹路作为诱导子区A、C的边界, 并将其归入子区C。将浑河的分支作为诱导子区D与子区B、C的边界, 将两侧的路网分别归入对应子区。经过对诱导子区边界进行调整得到调整后的诱导小区划分结果如图10所示。
利用小区饱和度、道路拥挤率和路网规模的限制3个特性参数对划分结果进行验证, 表3为4个小区的特性参数值。
| 表3 诱导小区特性参数值 Table 3 Guidance cell eigenvalues |
由表3中数据可知, 4个小区的3个特性参数值均在文中所提阈值之内, 所以本次诱导小区划分的结果合理。
通过建立基于随机游走算法的交通诱导小区划分模型, 考虑到交通诱导的目的以路段为节点将路网转化为网络图, 利用组合Dirichlet问题的求解方法对模型进行了求解。实验结果表明, 本文所建模型的划分结果满足交通诱导小区的特性参数阈值要求。本文所提方法可为城市交通诱导的分区研究提供一种有效的方法。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|