不完全网络的城乡公交一体化枢纽层级选址模型

引用本文

钟伟, 隽志才, 孙宝凤. 不完全网络的城乡公交一体化枢纽层级选址模型[J].吉林大学学报（工学版）, 2018,48(5): 1387-1397
ZHONG Wei, JUAN Zhi-cai, SUN Bao-feng. Hierarchical hub location model for integration of urban and rural public transport in an incomplete network[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1387-1397 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20180035
Permissions

不完全网络的城乡公交一体化枢纽层级选址模型

钟伟^1,², 隽志才^1,³, 孙宝凤¹

1.吉林大学交通学院,长春 130022

2.吉林财经大学亚泰工商管理学院,长春 130117

3.上海交通大学安泰经济与管理学院,上海 200240

通信作者:孙宝凤(1970-),女,教授,博士生导师.研究方向:服务网络规划.E-mail:sunbf@jlu.edu.cn

作者简介:钟伟(1981-),女,讲师,博士研究生.研究方向:物流系统规划,运输规划与管理.E-mail:zw.0211@163.com

基金:国家自然科学基金项目(50908099);教育部“春晖”计划合作科研项目(S2016012);吉林省科技发展计划项目(20150204021SF);吉林省科技发展计划软科学项目(20180418101FG)

摘要

以城乡公交一体化为背景,将城市公交枢纽和重点中心镇枢纽看作一个整体,构建了树形-星形-星形的多层级不完全网络。同时,考虑上述两层级枢纽的容量约束,以网络总成本最小为目标,建立了公交一体化层级枢纽选址的整数规划模型。借助于山东省某县城乡客运数据进行模型验证和参数敏感性分析,结果表明:该模型从城市中心区、城乡结合部和乡镇村一体化角度确定了城市公交枢纽和重点中心镇枢纽及其位置;与完全网络比较,不完全网络在成本增加不大的情况下枢纽各线路的流量更大,更利于发挥枢纽规模优势,提高线路的利用率。

关键词: 交通运输系统工程; 轴辐式网络; 不完全网络; 城乡公交一体化; 枢纽层级选址; 容量约束

中图分类号:U126 文献标志码:A 文章编号:1671-5497(2018)05-1387-11

Hierarchical hub location model for integration of urban and rural public transport in an incomplete network

ZHONG Wei^1,², JUAN Zhi-cai^1,³, SUN Bao-feng¹

1.College of Transportation,Jilin University,Changchun 130022,China

2.Yatai School of Business Administration,Jilin University of Finance and Economics,Changchun 130117,China

3.Antai College of Economics and Management, Shanghai Jiaotong University, Shanghai 200240, China

Abstract

Considering the integration of urban and rural public transport, taking the urban hubs and hubs in central towns as a whole, a tree-star-star network is constructed. Meanwhile, considering the capacity constraints of the hubs, a hierarchical hub location model for integration of urban and rural public transport is established that aims at the minimum total cost. Then, the model is validated and parameter sensitivity is analyzed using the actual urban and rural passenger transportation data. The results show that the hierarchical hub location model can determine hub locations in the cities and central towns from the perspective of the integration of urban, urban-rural junctions, and townships. Compared to complete network, hub links in the incomplete network carry larger volume of traffic with a modest cost increase, which can take advantages of hub scale and improve the utilization of the links.

Keyword: transportation systems engineering; hub-and-spoke network; incomplete network; integration of urban and rural public transport; hierarchical hub location; capacity constraints、

文章图片

0 引言

公交枢纽场站是城乡公交一体化实现的重要基础设施, 其选址和布局的合理与否关系到城乡居民出行的便利程度和城乡经济活动劳动力要素之间的流动效率。在城乡公交一体化环境下, 公交枢纽场站可分为城市公交枢纽和重点中心镇枢纽两类, 前者服务于城市内的客流和重点中心镇枢纽的客流; 后者服务于一般乡镇村的客流。

城乡公交枢纽选址问题是立足于城市公交枢纽体系的城市外拓进行扩充选址, 还是基于中心镇专项规划的枢纽单独选址, 目前的研究各持己见。例如, 尹继洁^[1]、王茂奎^[2]、高洁^[3]仅针对城市域的公交枢纽, 构建选址模型并求解; 而王超^[4]、姚霏^[5]则主要围绕重点中心镇枢纽, 采用覆盖模型进行选址。这些研究未能针对城乡结合区域的客流特征将城乡公交一体化两级枢纽进行一体化选址, 由此带来城市和乡镇区域两级枢纽之间互联互通成效低、公共资源利用率低和全网络运营成本高等问题。

鉴于轴辐网络具有可避免不必要的连接、有效降低成本等优越性^[6], 依托轴辐网络的枢纽多层级选址模型颇具代表性。最初轴辐网络研究基于枢纽间相互连接的基本假设, 即枢纽网络是一个完全网络^[7], 并围绕完全网络特征考虑需求不确定性、枢纽容量限制等因素进行拓展研究。代表性研究如Elmastas^[8]研究了土耳其货物公司的两枢纽三层级完全网络, 建立了考虑时间约束、无容量限制的层级枢纽选址模型, 确定了满足总运输成本最小的最优枢纽数量。继Elmastas研究之后, Yaman^[9]、Davari等^[10]和Karimi等^[11]构建了完全-星形-星形三层轴辐网络。不同的是, Yaman主要围绕货物运送时间如何影响总成本和中心枢纽位置展开讨论; Davari等和Karimi等则在Yaman构建的模型基础上, 分析了需求不确定性和枢纽容量两个因素对总成本和枢纽位置的影响。李婷婷等^[12]主要针对全国范围的城市综合客运枢纽构建了完全-完全-星形的三层轴辐网络, 分析了枢纽覆盖范围和城市分群对枢纽选址和总成本的影响。

研究发现, 完全网络结构易导致基础设施利用率低, 网络运营成本高、资源浪费严重等弊端, 因而不完全网络研究更具前景。国内外学者将不完全网络的类型细分为:树形网络^{[13, 14]}、星形网络^{[15, 16]}、环形网络^{[17, 18]}和多种结构结合的网络^[19]。其中, 树形和星形结构是典型的不完全网络, 主要应用于通讯和交通领域^[13], 如高铁运输网络、小件快递网络等。关于树形和星形结构的模型、方法、应用等研究大多集中于单层结构或者诸如星形-星形等两层网络结构^[20]。多层级货物运输的不完全轴辐网络研究如Alumur等^[21]、Dü kkanci等^[22]对研究树形和星形结构的城乡公交一体化不完全网络提供了借鉴和参考。

中国城乡公交一体化网络覆盖中心城区、重点中心镇、一般乡镇村三级城镇体系, 可以划分为3个层次^{[23, 24]}。其中, 第一层次连接城市中心区内公交枢纽的主干线; 第二层次连接城市中心区至各重点中心镇枢纽的次干线, 由此形成高频、快速的公交客运服务; 第三层次连接重点中心镇与一般乡镇村之间的支线。该网络的城市公交枢纽之间、重点中心镇之间、一般乡镇村之间互联互通较少, 属于不完全网络; 鉴于城市中心区和重点中心镇间具有高强度公共交通联系, 强度由城市中心区、重点中心镇向一般乡镇传递, 如水流由主干流向枝杈, 因而具有树状网络结构特点^{[25, 26]}。

本文针对城乡公交一体化网络, 构建树形-星形-星形轴辐网络, 建立层级枢纽选址模型, 该模型也是0-1混合整数规划模型, 其改进之处为:①将城市公交枢纽和重点中心镇枢纽一体化选址, 构建不完全网络的城乡公交一体化0-1混合整数规划模型; 同时确定两类枢纽位置, 并按照就近分配流量原则实现能力平衡。②构建了由城市公交枢纽、重点中心镇枢纽和需求点构成的“ 树形-星形-星形” 三层级网络。表征了中小城市城乡公交一体化网络的典型特征, 以及该网络拓扑结构下城乡客流特征。③考虑城市公交枢纽和重点中心镇枢纽的规模、容量、建设成本等对选址的直接影响, 建立了有容量约束的层级选址模型。

1 问题描述

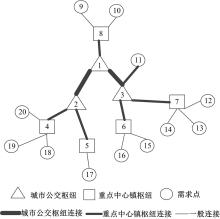
覆盖城市中心区、城乡结合部和一般乡镇村区域范围内的城乡公交系统, 由枢纽站点及其公交班线构成了城乡公交一体化网络, 既能满足城市公交功能的外延拓展, 又能实现乡镇农村客运的有效衔接。考虑研究区域的行政区划、路网、人口、经济、土地性质等因素, 将城市中心区、城乡结合部和一般乡镇村划分为若干交通小区, 每一个交通小区可看作一个网络节点, 它们构成了城乡公交一体化网络节点集合。其中, 城市中心区域中节点为城市公交枢纽备选点; 城乡结合部中节点为重点中心镇枢纽备选点。这些备选点分别构成了各自的备选点集合。本文研究的是具有代表性的“ 树形-星形-星形” 城乡公交一体化网络, 如图1所示。

	Figure Option View Download New Window
	图1 树形-星形-星形枢纽网络图Fig.1 Tree-star-star hub network

要解决的问题是, 在城市公交枢纽和重点中心镇枢纽的备选集合已知的基础上确定它们的位置, 城市公交枢纽之间的连接, 确定重点中心镇枢纽与城市公交枢纽的分配关系, 需求点到重点中心镇枢纽的分配关系, 达到使总成本最小的目标。

为了构建模型, 做了如下假设:

(1)每个节点只分配给一个枢纽点。

(2)城市公交枢纽之间、城市公交枢纽和重点中心镇枢纽之间的单位运输成本低于其他节点之间的单位运输成本, 分别用折减系数 $α_{1} 、 α_{2}$ 表示, $0 < α_{1}, α_{2} < 1,$ 文献[27, 28]已经证明。

(3)一个节点只能安放一个枢纽点。

2 模型构建

2.1 模型参数和变量

为了能计算分配路径上的流量, 本文参考文献[28, 29]提出的多商品流思想, 使用3个指数的变量表示枢纽间的客流量。同时, 为便于说明问题, 将模型参数和变量符号定义如下。

(1)参数

$I$ 为节点集合; $P_{b}$ 为城市公交枢纽备选点集合, $P_{b} \subseteq I; Q_{b}$ 为重点中心镇枢纽备选点集合, $Q_{b} \subseteq I, Q_{b} ⋂ P_{b} = \emptyset; H$ 为城市公交枢纽和重点中心镇枢纽备选点集合, $Q_{b} ⋃ P_{b} = H; w_{ij}$ 为从节点 $i$ 到节点 $j$ 的运输量, $i, j \in I, i \neq j; c_{ij}$ 为从节点 $i$ 到节点 $j$ 的单位运输成本, $c_{ij} = c_{ji}, i 、 j \in I, i \neq j; F_{1} 、 F_{2}$ 分别为城市公交枢纽和重点中心镇枢纽的建设成本; $M_{1} 、 M_{2}$ 分别为城市公交枢纽和重点中心镇枢纽的最大容量。

(2)变量

$x_{im} :$ 如果节点 $i$ 分配给枢纽 $m$ 时, $x_{im} = 1;$ 否则 $x_{im} = 0, i \in I, m \in H$ ; 如果在 $m$ 点建立枢纽, $x_{mm} = 1, m \in H 。$

$y_{mk} :$ 如果重点中心镇枢纽 $m$ 分配给城市公交枢纽 $k$ 时, $y_{mk} = 1;$ 否则 $y_{mk} = 0, m \in H, k \in P_{b};$ 如果在 $k$ 点建立城市公交枢纽, y_kk=1, k∈ P_b。

$z_{kl} :$ 如果城市公交枢纽 $k$ 和 $l$ 间有连接, z_kl=1, 否则 $z_{kl} = 0, k \in P_{b}, l \in P_{b} \ {k} 。$

$u_{mk} :$ 如果城市公交枢纽和重点中心镇枢纽之间有连接, $u_{mk} = 1;$ 否则u_mk=0, m∈ H, k∈ H。

$g_{kl}^{i} :$ 起点为 $i$ 的城市公交枢纽 $k$ 和 $l$ 间的运输量 $i \in I, k \in P_{b}, l \in P_{b} \ {k} 。$

$h_{mk}^{i} :$ 起点为 $i$ 的重点中心镇枢纽 $m$ 和城市公交枢纽 $k$ 之间的运输量, $i \in I, m \in H, k \in H 。$

2.2 模型的建立

比较分析文献[9, 12]完全网络下的枢纽层级选址模型, 对它的网络结构、流量平衡等进行解析, 重新界定不完全网络, 树形网络下枢纽连接关系、流量平衡和容量约束如下:

$\begin{array}{l} \min \sum_{i \in I} \sum_{s \in I} (w_{is} + w_{si}) \sum_{m \in H} c_{im} x_{im} + \\ \sum_{i \in I} \sum_{k \in P_{b}} \sum_{l \in P_{b} \ {k}} α_{1} c_{kl} g_{kl}^{i} + \sum_{i \in I} \sum_{m \in H} \sum_{k \in P_{b}} α_{2} c_{mk} h_{mk}^{i} + \\ \sum_{k \in P_{b}} F_{1} y_{kk} + \sum_{m \in Q_{b}} F_{2} x_{mm} (1) \\ s.t. \sum_{m \in H} x_{im} = 1, \forall i \in I (2) \\ x_{kk} = y_{kk}, \forall k \in P_{b} (3) \\ x_{im} \leq x_{mm}, \forall i \in I, m \in H (4) \\ \sum_{k \in P_{b}} y_{mk} = x_{mm}, \forall m \in H (5) \\ y_{mk} \leq y_{kk}, \forall m \in H, k \in P_{b} (6) \\ 2 z_{kl} \leq y_{kk} + y_{ll}, \forall k \in P_{b}, l \in P_{b} \ \{k\} (7) \\ z_{kl} = z_{lk}, \forall k \in P_{b}, l \in P_{b} \ \{k\} (8) \\ \sum_{l \in P_{b}} \sum_{k \in P_{b}} z_{kl} = 2 (\sum_{k \in P_{b}} y_{kk} - 1), \forall k \neq l (9) \\ u_{mk} = y_{mk}, \forall m \in H, k \in P_{b} \ \{m\} (10) \\ u_{mk} = u_{km}, \forall m \in H, k \in H (11) \\ u_{mk} = 0, \forall m \in Q_{b}, k \in Q_{b} (12) \\ \sum_{n \in H \ \{m\}} h_{mn}^{i} - \sum_{n \in H \ \{m\}} h_{nm}^{i} = \sum_{s \in I} w_{is} (x_{im} - x_{sm}) \\ \forall i \in I, m \in H, m \notin P_{b} (13) \\ \sum_{l \in H \ \{j\}} h_{jl}^{i} + \sum_{k \in P_{b} \ \{j\}} g_{jk}^{i} - \sum_{k \in P_{b} \ \{j\}} g_{kj}^{i} - \sum_{l \in H \ \{j\}} h_{lj}^{i} = \\ \sum_{s \in I} w_{is} (x_{ij} - x_{sj}), \forall i \in I, j \in P_{b} (14) \\ g_{kl}^{i} \leq z_{kl} \sum_{s \in I} w_{is} (15) \\ \forall k \in P_{b}, l \in P_{b} \ \{k\}, i \in N \\ h_{mk}^{i} \leq u_{mk} \sum_{s \in I} w_{is} (16) \\ \forall i \in I, m \in H, k \in H \ \{m\} \\ \sum_{i \in I} \sum_{j \in I} w_{ij} x_{im} \leq M_{2} x_{mm}, \forall m \in Q_{b} (17) \\ \sum_{i \in I} \sum_{m \in Q_{b}} h_{mk}^{i} + \sum_{i \in I} \sum_{j \in I} w_{ij} x_{ik} \leq M_{1} y_{kk} (18) \\ \forall k \in P_{b} \\ g_{kl}^{i} \geq 0, \forall i, k, l, k \neq l (19) \\ h_{mk}^{i} \geq 0, \forall i, m, k, m \neq k (20) \\ x_{im} \in \{0, 1\}, \forall i \in I, m \in H (21) \\ y_{mk} \in \{0, 1\}, \forall m \in Q_{b}, k \in P_{b} (22) \\ z_{kl} \in \{0, 1\}, \forall k \in P_{b}, l \in P_{b} \ \{k\} (23) \end{array}$

目标函数(1)表示网络总成本最小, 即运输成本和枢纽建设成本之和最小, 第一项表示分配成本, 第二项为城市公交枢纽间的运输成本, 第三项为重点中心镇枢纽和城市公交枢纽间的运输成本, 第四项和第五项分别为城市公交枢纽和重点中心镇枢纽的建设成本。

约束(2)保证节点 $i$ 只分配给一个枢纽点; 约束(3)保证重点中心镇枢纽点不能在城市公交枢纽备选集合中选择; 约束(4)保证节点 $i$ 分配给的点一定是枢纽点; 约束(5)和(6)保证重点中心镇枢纽 $m$ 只分配给一个城市公交枢纽 $k,$ 而且分配给的点一定是枢纽点; 约束(7)和(8)表示只有当连接的两个点都是枢纽时, 城市公交枢纽间才有连接; 约束(9)表示城市公交枢纽间是树形网络结构; 约束(10)和(11)表示重点中心镇枢纽和城市公交枢纽之间有连接, 而且连接是无方向的; 约束(12)表示两个重点中心镇枢纽之间没有连接; 约束(13)和(14)分别表示重点中心镇枢纽和城市公交枢纽的流量平衡。约束(15)表示如果城市公交枢纽点 $k$ 和 $l$ 间没有连接, 则 $k$ 和 $l$ 间的运输量为0; 约束(16)表示如果乡镇重点中心镇枢纽 $m$ 和城市公交枢纽 $k$ 之间没有连接, 则它们之间的运输量为0; 约束(17)和(18)分别是重点中心镇枢纽和城市公交枢纽的容量约束; 约束(19)和(20)是运输量的非负约束。约束(21)(22)(23)是0-1整数约束。

3 模型求解与实例分析

3.1 模型求解

树形网络下的枢纽层级选址问题属于NP难问题, 文献[20]已证明。该模型是0-1混合整数规划模型, 可以采用分支切割法求解。分支切割法是分支定界法与割平面法的结合, 该方法是通过对分支切割树的不断扩展和切割来寻优的^[30]。优化软件Cplex在求解混合整数规划模型时采用的就是分支切割法, 因此, 本文在Intel Core i7-4790CPU@3.60 GHz, 内存16 GB, 操作系统Windows7环境下采用Cplex12.5.1进行模型求解。

3.2 实例分析

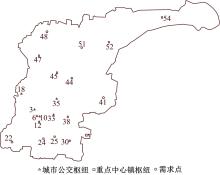
以山东省某县的城乡规划区域为研究对象, 该区域包含20个交通小区, 如图2所示, 各交通小区间的距离和客流量如表1和表2所示。依据城乡公交一体化网络层级划分, 在城市中心区选择7个交通小区作为城市公交枢纽备选点集合, 在城乡结合部选择10个交通小区作为重点中心镇枢纽备选点集合。由实例可知, 该区域单位运输成本为0.2元/(人· 公里); 两级枢纽之间折减系数分别为 $α_{1} = 0.8, α_{2} = 0.9;$ 两级枢纽建设成本分别为 $F_{1} = 3000000$ 元, $F_{2} = 1500000$ 元; 城市公交枢纽的容量范围为5000~10 000人次/日, 重点中心镇枢纽的容量范围为2000~5000人次/日。

	Figure Option View Download New Window
	图2 20个节点及枢纽备选点的分布图Fig.2 Distribution for 20 nodes and alternative hubs

表1 节点之间的客流量 Table 1 Passenger volumes between nodes 人次

表2 节点之间的距离 Table 2 Distances between nodes km

小区	3	6	10	12	18	22	24	25	30	33	35	38	41	44	45	47	48	51	52	54
3	0.00	1.83	2.39	3.59	5.90	10.97	8.34	9.49	13.31	5.59	7.10	9.55	20.10	13.16	12.06	15.83	21.78	22.05	27.53	46.56
6	1.83	0.00	0.83	1.75	7.67	10.20	6.51	7.74	11.71	4.81	7.39	8.56	19.75	13.86	13.26	17.49	23.40	23.04	28.21	46.94
10	2.39	0.83	0.00	1.50	8.29	10.73	6.19	7.10	10.97	4.03	6.87	7.74	19.01	13.45	13.10	17.64	17.64	22.74	27.76	46.37
12	3.59	1.75	1.50	0.00	9.37	9.70	4.77	6.13	10.28	4.71	8.09	7.96	19.63	14.76	14.57	19.13	24.99	24.13	29.00	47.42
18	5.90	7.67	8.29	9.37	0.00	13.46	13.98	15.39	19.15	10.84	10.39	14.76	23.66	14.28	11.44	12.28	18.26	21.45	27.88	47.57
22	10.97	10.20	10.73	9.70	13.46	0.00	9.39	12.73	16.97	14.40	17.58	17.20	29.16	24.03	22.96	25.63	31.65	33.01	38.40	57.09
24	8.34	6.51	6.19	4.77	13.98	9.39	0.00	3.37	7.64	7.45	11.55	8.68	20.59	18.19	18.74	23.78	29.57	27.75	31.95	49.49
25	9.49	7.74	7.10	6.13	15.39	12.73	3.37	0.00	4.45	6.39	10.41	6.08	17.60	16.67	17.94	23.75	29.27	26.21	29.83	46.78
30	13.31	11.71	10.97	10.28	19.15	16.97	7.64	4.45	0.00	8.85	12.10	6.26	15.29	17.32	19.53	26.03	31.16	26.49	29.07	44.73
33	5.59	4.81	4.03	4.71	10.84	14.40	7.45	6.39	8.85	0.00	4.13	3.98	14.99	10.74	11.58	17.45	22.90	20.30	24.66	42.78
35	7.10	7.39	6.87	8.09	10.39	17.58	11.55	10.41	12.10	4.13	0.00	6.01	13.36	6.71	7.57	13.95	19.10	16.22	20.91	39.57
38	9.55	8.56	7.74	7.96	14.76	17.20	8.68	6.08	6.26	3.98	6.01	0.00	12.01	11.14	13.30	19.95	24.94	20.50	23.78	40.83
41	20.10	19.75	19.01	19.63	23.66	29.16	20.59	17.60	15.29	14.99	13.36	12.01	0.00	11.38	15.64	22.56	25.20	15.96	15.44	29.44
44	13.16	13.86	13.45	14.76	14.28	24.03	18.19	16.67	17.32	10.74	6.71	11.14	11.38	0.00	4.27	11.28	14.81	9.58	14.38	33.57
45	12.06	13.26	13.10	14.57	11.44	22.96	18.74	17.94	19.53	11.58	7.57	13.30	15.64	4.27	0.00	7.22	11.64	10.18	16.44	36.19
47	15.83	17.49	17.64	19.13	12.28	25.63	23.78	23.75	26.03	17.45	13.95	19.95	22.56	11.28	7.22	0.00	6.02	12.19	19.36	38.98
48	21.78	23.40	17.64	24.99	18.26	31.65	29.57	29.27	31.16	22.90	19.10	24.94	25.20	14.81	11.64	6.02	0.00	11.22	17.87	36.40
51	22.05	23.04	22.74	24.13	21.45	33.01	27.75	26.21	26.49	20.30	16.22	20.50	15.96	9.58	10.18	12.19	11.22	0.00	7.17	26.88
52	27.53	28.21	27.76	29.00	27.88	38.40	31.95	29.83	29.07	24.66	20.91	23.78	15.44	14.38	16.44	19.36	17.87	7.17	0.00	19.85
54	46.56	46.94	46.37	47.42	47.57	57.09	49.49	46.78	44.73	42.78	39.57	40.83	29.44	33.57	36.19	38.98	36.40	26.88	19.85	0.00

表2 节点之间的距离 Table 2 Distances between nodes km

实例分析旨在Cplex精确求解的基础上应用该区域的城乡公交数据验证提出的模型有效性和参数敏感性。其中, 组合情景依据两级枢纽容量的上、下限 $M_{1}$ 和 $M_{2}$ 的取值而构建。结合实例, 以完全网络作为对比基础(称为网络2, 见图3), 一方面, 分析城乡公交一体化不完全网络结构(称为网络1, 见图1)对枢纽层级选址方案和网络总成本的影响; 另一方面, 分析主要参数(容量和折减系数)对枢纽层级选址方案和网络总成本的影响。

	Figure Option View Download New Window
	图3 完全网络结构图Fig.3 Complete network structure

经Cplex求解, 获得不同容量约束下两种网络结构的最优解如表3所示。

表3 不同容量约束下两种网络结构的最优解 Table 3 Optimizations for two kinds of network structures by different capacity constraints

	容量约束	情景1	情景2	情景3	情景4	情景5	情景6
	容量约束	$\begin{array}{l} (M_{1} = 5000, \\ M_{2} = 2000) \end{array}$	$\begin{array}{l} (M_{1} = 8000, \\ M_{2} = 2000) \end{array}$	$\begin{array}{l} (M_{1} = 10000, \\ M_{2} = 2000) \end{array}$	$\begin{array}{l} (M_{1} = 5000, \\ M_{2} = 5000) \end{array}$	$\begin{array}{l} (M_{1} = 8000, \\ M_{2} = 5000) \end{array}$	$\begin{array}{l} (M_{1} = 10000, \\ M_{2} = 5000) \end{array}$
网络结构1	网络总成本/元	22 678 375.8	15 136 356.4	12 128 898.9	21 130 467.1	15 108 030.1	12 110 784.7
	运输成本/元	178 381.0	136 356.4	128 898.9	130 468.0	108 030.1	110 784.7
	城市公交枢纽编号	3, 6, 10, 12, 18, 33, 35	3, 10, 12, 33, 35	6, 10, 33, 35	3, 6, 10, 12, 33, 35	6, 10, 33, 35	10, 33, 35
	重点中心镇枢纽编号	54	-	-	38, 52	45, 52	38, 52
	计算时间/s	13.24	37.88	5.79	7387.03	24135.01	482.67
网络结构2	网络总成本/元	22674063.2	15 134 101.2	12 126 819.0	13 631 032.3	13 617 059.0	12 102 075.8
	运输成本/元	174 068.0	134 106.0	126 819.0	131 032.3	117 059.0	102 075.8
	城市公交枢纽编号	3, 6, 10, 12, 18, 33, 35	3, 6, 10, 33, 35	10, 12, 33, 35	10	6	10, 33, 35
	重点中心镇枢纽编号	54	-	-	24, 25, 38, 44, 45, 51, 52	24, 25, 38, 44, 45, 51, 52	51, 52
	计算时间/s	11.37	15.12	13.32	318.85	2679.91	1328.88
网络总成本增加百分比/%		0.019	0.015	0.017	55.017	10.949	0.072
运输成本增加百分比/%		2.478	1.678	1.640	-0.431	-7.713	8.532

表3 不同容量约束下两种网络结构的最优解 Table 3 Optimizations for two kinds of network structures by different capacity constraints

3.2.1 枢纽选址方案比较

同一网络结构下, 情景1~情景6为不同枢纽容量组合, 其选址方案如表3所示。不同情景下, 选址方案差异较大, 其对应的网络总成本和运输成本亦变化较大。例如, 网络1中情景1的选址方案为7个城市公交枢纽(3, 6, 10, 12, 18, 33, 35), 1个重点中心镇枢纽(54); 而情景3的选址方案为4个城市公交枢纽(6, 10, 33, 35), 重点中心镇枢纽没有选择, 变化较明显。情景1中网络总成本为22 678 375.8元, 情景3中网络总成本为12 128 898.9元, 减少了将近47%; 运输成本也减少了将近30%, 差异较明显。类似的, 在网络2中也会发现此变化。

同一情景内, 两种网络的选址方案差异较小, 其对应的网络总成本和运输成本变化也较小。以情景6为例, 网络1的选址方案为3个城市公交枢纽(10, 33, 35), 2个重点中心镇枢纽(38, 52); 网络2的选址方案为3个城市公交枢纽(10, 33, 35), 2个重点中心镇枢纽(51, 52)。除了以重点中心镇枢纽51替代了枢纽38, 其他没有变化。网络1比网络2的总成本增加了0.072%, 运输成本增加了8.532%, 成本变化不是很大。可见, 城乡公交一体化网络结构对枢纽选址和成本都会产生影响, 但影响不是很大。

就两级枢纽的数量和位置来看, 网络1中两级枢纽容量差较大时, 如情境3所示, 即重点中心镇枢纽容量M₂取下限2000, 城市公交枢纽容量M₁取上限10 000, 此时容量的限制使得需求点无法分配给各重点中心镇枢纽, 而直接将其分配给城市公交枢纽。两级枢纽容量差较小时, 如情景4所示, 容量差为0, 亦出现了城市公交枢纽数量多, 重点中心镇枢纽数量少的情况。可见, 不管容量如何变化, 不完全网络中城市公交枢纽选择的数量较多, 重点中心镇枢纽选择的数量却很少。同时, 在不完全网络中, 节点10, 33和35始终被选为城市公交枢纽, 主要因为这3个点不仅流量较大, 从距离角度考虑路径成本还较小。

网络2中, 重点中心镇枢纽的容量M₂较小, 如M₂=2000时, 几种情景下城市公交枢纽的数量均较多, 重点中心镇枢纽的数量均较少。当两级枢纽容量差较大时(见情景3), 城市公交枢纽的数量要少于容量差较小(见情景1)的情况。相反, 当重点中心镇枢纽的容量M₂较大, 如M₂=5000时, 城市公交枢纽的数量较少, 而重点中心镇枢纽的数量却较多。当两级枢纽容量差较大时(见情景6), 重点中心镇枢纽的数量要少于容量差较小(见情景4)的情况。同时, 在完全网络中, 除情景5外, 节点10始终是城市公交枢纽。

由此, 在不完全和完全两种网络结构中, 两级枢纽的容量对枢纽的位置和数量均会产生显著的影响。

3.2.2 网络流量的比较

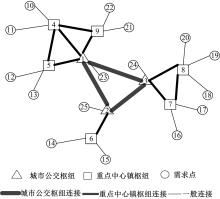
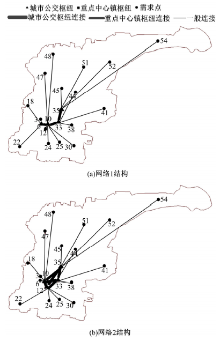
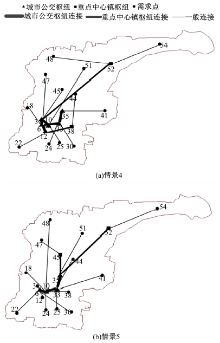
图4为情景3的网络1和网络2结构图。两种网络结构选择的城市公交枢纽均为4个, 网络1的枢纽间的连接有3个, 网络2的枢纽间的连接有6个。由于网络1中枢纽间的不完全连接, 客流可能要经过多于一个的枢纽连接, 所以成本增加, 这实际上从决策角度来说是不合算的。但在网络2中, 不是所有的枢纽连接都有大量客流经过的。把图4(a)和(b)的9个枢纽连接按照流经客流的大小进行排序, 如表4所示。可以看出, 网络1的3个连接位居前三位, 其中点10和33的流量最大, 而网络2的6个连接都排在后面, 有的枢纽连接只有很少客流经过, 网络线路的利用率明显不高。因此, 与完全网络相比, 不完全网络的枢纽间客流量较大, 更利于规模经济的应用, 更利于发挥轴辐网络的优势。

	Figure Option View Download New Window
	图4 情景3的两种网络结构Fig.4 Two kinds of network in case 3

表4 两种网络枢纽连接上的客流量 Table 4 Passenger volumes of hub links for two kinds of network

3.2.3 运输成本的比较

由表3可知, 除了情景4和情景5, 其他情景下网络1的总成本和运输成本普遍要高于网络2, 最大高出55.017%, 最小高出0.015%。这是因为不完全网络的连通性没有完全网络的连通性好。

在两种网络结构中, 一级枢纽容量不变, 随着另一级枢纽容量增加, 网络总成本和运输成本均减小。如网络1的情景4和情景5, 重点中心镇枢纽容量 $M_{2} = 5000,$ 城市公交枢纽容量 $M_{1}$ 由5000增加到8000, 网络总成本和运输成本分别降低28.50%和17.20%。类似的, 在网络2中也有相同规律可循。这是因为, 枢纽容量增加, 需求点可以分配给路径成本最小的枢纽点, 并且分配更集中, 节点间路径也短, 所以枢纽间的规模优势更明显, 成本减少。如图5所示, 图5(a)枢纽数量多, 分配分散, 节点间路径长; 图5(b)枢纽数量少, 分配更集中, 节点间路径短。假设要从节点22到节点30, 在图5(a)中需经过路线22-12-6-33-30, 而在图5(b)中仅经过路线22-6-30, 成本更少。

	Figure Option View Download New Window
	图5 两种情景的网络1结构Fig.5 Network 1 in two cases

3.2.4 计算速度的比较

在两种网络中, 除情景3和情景6, 其他情景下, 网络1的计算时间都长于网络2的计算时间。如情景4, 网络1计算时间为7387.03 s; 网络2的计算时间为318.85 s, 增加了近23倍。可见, 不完全网络的平均求解时间明显高于完全网络, 说明不完全网络的求解速度慢于完全网络。

3.2.5 折减系数的影响

根据文献[27, 28], 折减系数在0~1区间变化, 借鉴货物运输中折减系数的确定规律, 考虑到城乡公交客运流量特点, 本文确定折减系数的取值范围为[0.6, 1]。以情景6为例, 计算结果如表5和表6所示。

表5 不同折减系数下网络1的成本与枢纽变化情况 Table 5 Cost and hub location for network 1 with different discount factor

折减系数		总成本/元	运输成本/元	城市公交枢纽编号	重点中心镇枢纽编号
$α_{1}$	$α_{2}$	总成本/元	运输成本/元	城市公交枢纽编号	重点中心镇枢纽编号
0.6	0.6	12 102 616.6	102 617.0	10, 33, 35	38, 52
0.6	0.7	12 104 388.4	104 389.0	10, 33, 35	38, 52
0.6	0.8	12 106 160.2	106 160.0	10, 33, 35	38, 52
0.6	0.9	12 107 932.0	107 932.0	10, 33, 35	38, 52
0.6	1.0	12 109 703.8	109 704.0	10, 33, 35	38, 52
0.7	0.7	12 105 814.7	105 815.4	10, 33, 35	38, 52
0.7	0.8	12 107 586.5	107 586.5	10, 33, 35	38, 52
0.7	0.9	12 109 358.3	109 358.4	10, 33, 35	38, 52
0.7	1.0	12 111 130.1	111 130.4	10, 33, 35	38, 52
0.8	0.8	12 109 012.9	109 013.0	10, 33, 35	38, 52
0.8	0.9	12 110 784.7	110 785.0	10, 33, 35	38, 52
0.8	1.0	12 112 556.5	112 557.0	10, 33, 35	38, 52
0.9	0.9	12 112 211.0	112 211.0	10, 33, 35	38, 52
0.9	1.0	12 113 982.8	113 983.0	10, 33, 35	38, 52

表5 不同折减系数下网络1的成本与枢纽变化情况 Table 5 Cost and hub location for network 1 with different discount factor

表6 不同折减系数下网络2的成本与枢纽变化情况 Table 6 Cost and hub location for network 2 with different discount factor

折减系数		总成本/元	运输成本/元	城市公交枢纽编号	重点中心镇枢纽编号
$α_{1}$	$α_{2}$	总成本/元	运输成本/元	城市公交枢纽编号	重点中心镇枢纽编号
0.6	0.6	12 092 396.6	92 396.5	10, 33, 35	51, 52
0.6	0.7	12 094 517.4	94 517.2	10, 33, 35	51, 52
0.6	0.8	12 096 638.3	96 638.2	10, 33, 35	51, 52
0.6	0.9	12 098 759.1	98 758.2	10, 33, 35	51, 52
0.6	1.0	12 100 879.9	100 879.2	10, 33, 35	51, 52
0.7	0.7	12 096 175.8	96 175.0	10, 33, 35	51, 52
0.7	0.8	12 098 296.6	98 297.0	10, 33, 35	51, 52
0.7	0.9	12 100 417.5	100 417.0	10, 33, 35	51, 52
0.7	1.0	12 102 538.3	102 538.0	10, 33, 35	51, 52
0.8	0.8	12 099 955.0	99 955.0	10, 33, 35	51, 52
0.8	0.9	12 102 075.8	102 075.0	10, 33, 35	51, 52
0.8	1.0	12 104 196.7	104 196.0	10, 33, 35	51, 52
0.9	0.9	12 103 734.2	103 734.0	10, 33, 35	51, 52
0.9	1.0	12 105 855.0	105 854.0	10, 33, 35	51, 52

表6 不同折减系数下网络2的成本与枢纽变化情况 Table 6 Cost and hub location for network 2 with different discount factor

对于网络1, 由表5可知, 当 $α_{1}$ 不变、 $α_{2}$ 减小时, 两层级枢纽布局都没有发生变化, 但总成本和运输成本都减小; 当 $α_{2}$ 不变、 $α_{1}$ 减小时, 两层级枢纽的布局也没有变化, 但总成本和运输成本却在减小。这说明折减系数对不完全网络的总成本和运输成本有影响; 而对其枢纽的数量和位置的影响并不显著。

对于网络2, 由表6可知, $α_{1}$ 和 $α_{2}$ 对总成本和运输成本有影响, 对两层级枢纽数量和位置没有显著影响。

可见, 折减系数对城乡公交一体化网络的总成本和运输成本会产生一定的影响, 但对枢纽布局影响并不显著。

4 结论

(1)对城市公交枢纽和重点中心镇枢纽一体化选址, 构建多层级选址模型。所建模型能同时确定两级枢纽的数量和位置, 保证网络总成本最小。同时考虑两级枢纽选址更有助于发挥枢纽规模优势, 各级枢纽间流量的分配、线路资源的整合以及枢纽利用率得到提高, 从而保证城乡居民便捷、高效的出行。

(2)从流量与成本角度出发, 构建了树形-星形-星形的不完全网络, 并与完全网络的结果进行了对比。结果表明, 大多数情况下, 不完全网络在求解时间和运输成本上虽然优势不是很明显, 但由于不是所有枢纽间都有连接, 也就使得流量能够大规模聚集在枢纽点上, 更有利于发挥规模优势, 提高网络线路的利用率; 而且不完全网络能够达到完全网络所提供的服务水平。

(3)实例研究表明, 两层级枢纽容量的变化不仅影响枢纽的数量和位置, 对运输成本也有较大影响。更重要的是, 立足于两层级枢纽的容量组合进行双层枢纽选址, 对城乡公交一体化网络更具研究价值, 这是因为每一种枢纽容量组合情景体现了适合一定客流需求特征的上下两级枢纽的能力平衡关系, 而城乡公交一体化网络拟解决的关键问题正是城乡结合部公交设施能力接驳不协调的问题。

(4)未来的研究将考虑公交服务水平、地区经济发展差异、网络线路成本等因素, 构建更符合实际特征的模型。同时, 对于中大规模的多层级枢纽选址问题算法的设计也是要进一步研究的主要内容。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	尹继洁. 基于城乡客运一体化的客运站布局规划研究[D]. 青岛: 山东科技大学交通学院, 2011. Yin Ji-jie. Study on macro-layout of passenger station under urban-rural passenger transport integration[D]. Qingdao: College of Transportation, Shand ong University of Science and Technology, 2011. [本文引用:1]
[2]	王茂奎. 基于城乡统筹发展的客运一体化研究[D]. 成都: 西南交通大学交通运输与物流学院, 2010. Wang Mao-kui. Research on integrated passenger transport system based on urban and rural coordination and development[D]. Chengdu: School of Transportation and Logistics, Southwest Jiaotong University, 2010. [本文引用:1]
[3]	高洁. 城乡客运一体化下客运站的布局研究[D]. 西安: 长安大学汽车学院, 2008. Gao Jie. Study on layout of passenger station under urban-rural passenger transport integration[D]. Xi'an: School of Automobile, Chang'an University, 2008. [本文引用:1]
[4]	王超. 城乡客运一体化发展模式研究[D]. 西安: 长安大学公路学院, 2010. Wang Chao. Study on of integrated development of urban and rural passenger transport[D]. Xi'an: School of Highway, Chang'an University, 2010. [本文引用:1]
[5]	姚霏. 西部县域城乡客运交通一体化体系研究[D]. 武汉: 武汉理工大学交通学院, 2013. Yao Fei. Research on urban and rural passenger transport integration system in western county of China[D]. Wuhan: School of Transportation, Wuhan University of Technology, 2013. [本文引用:1]
[6]	Alumur S, Kara B Y. Network hub location problems: the state of the art[J]. European Journal of Operational Research, 2008, 190(1): 1-21. [本文引用:1]
[7]	Alumur S, Kara B Y, Karasan O E. The design of single allocation incomplete hub networks[J]. Transportation Research Part B, 2009, 43(10): 936-951. [本文引用:1]
[8]	Elmastas S. Hub location problem for air-ground transportation systems with time restrictions[D]. Ankara: Department of Industrial Engineering, Bilkent University, 2006. [本文引用:1]
[9]	Yaman H. The hierarchical hub median problem with single assignment[J]. Transportation Research Part B, 2009, 43(6): 643-658. [本文引用:1]
[10]	Davari S, Zarand i M H F. The single-allocation hierarchical hub median location problem with fuzzy demand s[J]. African Journal of Business Management, 2012, 6(1): 347-360. [本文引用:1]
[11]	Karimi M, Eydi A R, Korani E. Modeling of the capacitated single allocation hub location problem with a hierarchical approach[J]. International Journal of Engineering, 2014, 27(4): 573-586. [本文引用:1]
[12]	李婷婷, 宋瑞, 何世伟, 等. 基于分层布局的城市群综合客运枢纽优化模型[J]. 中国公路学报, 2016, 29(2): 116-122. Li Ting-ting, Song Rui, He Shi-wei, et al. Optimization model of comprehensive passenger hub in urban agglomeration based on hierarchical layout[J]. China Journal of Highway and Transport, 2016, 29(2): 116-122. [本文引用:1]
[13]	Contreras I, Fernández E, Marín A. Tight bounds from a path based formulation for the tree of hub location problem[J]. Computers & Operations Research, 2009, 36(12): 3117-3127. [本文引用:2]
[14]	Sedehzadeh S, Tavakkoli-Moghaddam R, Baboli A, et al. Optimization of a multi-modal tree hub location network with transportation energy consumption: a fuzzy approach[J]. Journal of Intellingent & Fuzzy Systems, 2016, 30(1): 43-60. [本文引用:1]
[15]	Yaman H. Star p-hub median problem with modular arc capacities[J]. Computers & Operations Research, 2008, 35(9): 3009-3019. [本文引用:1]
[16]	Yaman H, Elloumi S. Star p-hub center problem and star p-hub median problem with bounded path lengths[J]. Computers & Operations Research, 2012, 39(11): 2725-2732. [本文引用:1]
[17]	Lee C H, Ro H B, Tcha D W. Topological design of a two-level network with ring-star configuration[J]. Computers & Operations Research, 1993, 20(6): 625-637. [本文引用:1]
[18]	Wang Z, Lin C, Chan C K. Demonstration of a single-fiber self-healing CWDM metro access ring network with unidirectional OADM[J]. IEEE Photonics Technology Letters, 2006, 18(1): 163-165. [本文引用:1]
[19]	Klincewicz J G. Hub location in backbone tributary network design[J]. Location Science, 1998, 6(1-4): 307-335. [本文引用:1]
[20]	Contreras I, Fernández E, Marín A. The tree of hubs location problem[J]. European Journal of Operational Research, 2010, 202(2): 390-400. [本文引用:2]
[21]	Alumur S A, Yaman H, Kara B Y. Hierarchical multimodal hub location problem with time-definite deliveries[J]. Transportation Research Part E, 2012, 48(6): 1107-1120. [本文引用:1]
[22]	Dükkanci O, Kara B Y. Routing and scheduling decisions in the hierarchical hub location problem[J]. Computers & Operations Research, 2017, 85: 45-57. [本文引用:1]
[23]	吴公勇. 城乡公交一体化实施研究[D]. 武汉: 华中科技大学土木工程与力学学院, 2007. Wu Gong-yong. Research on implementing of integration of public transit in urban and suburbs[D]. Wuhan: School of Engineering & Mechanics, Huazhong University of Science and Technology, 2007. [本文引用:1]
[24]	赵永胜. 中小城市城乡公交一体化线网布局及运行组织研究[D]. 南京: 南京林业大学汽车与交通工程学院, 2011. Zhao Yong-sheng. Study on the network layout and organization for the integration of urban and rural public transportation in small and medium-sized city[D]. Nanjing: School of Automotive and Transportation Engineering, Nanjing Forestry University, 2011. [本文引用:1]
[25]	唐清. 城市群城乡道路公交一体化线网布局规划研究[D]. 武汉: 武汉理工大学交通学院, 2013. Tang Qing. Layout planning study of urban-rural bus public transport network in urban agglomeration[D]. Wuhan: School of Transportation, Wuhan University of Technology, 2013. [本文引用:1]
[26]	过秀成, 姜晓红. 城乡公共客运规划与组织[M]. 北京: 清华大学出版社, 2011. [本文引用:1]
[27]	O'Kelly M E. Hub location with flow economies of scale[J]. Transportation Research Part B, 1998, 32(8): 605-616. [本文引用:1]
[28]	Ernst A T, Krishnamoorthy M. Efficient algorithms for the uncapacitated single allocation p-hub median problem[J]. Location Science, 1996, 4(3): 139-154. [本文引用:1]
[29]	Ebery J. Solving large single allocation p-hub problems with two or three hubs[J]. European Journal of Operational Research, 2001, 128(2): 447-458. [本文引用:1]
[30]	崔建国, 周鹏甲, 于明月, 等. 基于资源约束的飞机保障任务调配方法研究[J]. 控制工程, 2017, 24(9): 1897-1902. Cui Jian-guo, Zhou Peng-jia, Yu Ming-yue, et al. Research on the method of aircraft support operation scheduling with limited resources[J]. Control Engineering of China, 2017, 24(9): 1897-1902. [本文引用:1]

2011

0.0

... 例如,尹继洁^[1]、王茂奎^[2]、高洁^[3]仅针对城市域的公交枢纽,构建选址模型并求解 ...

2010

0.0

... 例如,尹继洁^[1]、王茂奎^[2]、高洁^[3]仅针对城市域的公交枢纽,构建选址模型并求解 ...

2008

0.0

... 例如,尹继洁^[1]、王茂奎^[2]、高洁^[3]仅针对城市域的公交枢纽,构建选址模型并求解 ...

2010

0.0

... 而王超^[4]、姚霏^[5]则主要围绕重点中心镇枢纽,采用覆盖模型进行选址 ...

2013

0.0

... 而王超^[4]、姚霏^[5]则主要围绕重点中心镇枢纽,采用覆盖模型进行选址 ...

2008

0.0

... 鉴于轴辐网络具有可避免不必要的连接、有效降低成本等优越性^[6],依托轴辐网络的枢纽多层级选址模型颇具代表性 ...

2009

0.0

... 最初轴辐网络研究基于枢纽间相互连接的基本假设,即枢纽网络是一个完全网络^[7],并围绕完全网络特征考虑需求不确定性、枢纽容量限制等因素进行拓展研究 ...

2006

0.0

... 代表性研究如Elmastas^[8]研究了土耳其货物公司的两枢纽三层级完全网络,建立了考虑时间约束、无容量限制的层级枢纽选址模型,确定了满足总运输成本最小的最优枢纽数量 ...

2009

0.0

... 继Elmastas研究之后,Yaman^[9]、Davari等^[10]和Karimi等^[11]构建了完全-星形-星形三层轴辐网络 ...

2012

0.0

... 继Elmastas研究之后,Yaman^[9]、Davari等^[10]和Karimi等^[11]构建了完全-星形-星形三层轴辐网络 ...

2014

0.0

... 继Elmastas研究之后,Yaman^[9]、Davari等^[10]和Karimi等^[11]构建了完全-星形-星形三层轴辐网络 ...

2016

0.0

... 李婷婷等^[12]主要针对全国范围的城市综合客运枢纽构建了完全-完全-星形的三层轴辐网络,分析了枢纽覆盖范围和城市分群对枢纽选址和总成本的影响 ...

2009

0.0