基于多种群遗传算法的自动化立体库货位优化

引用本文

焦玉玲, 张鹏, 田广东, 邢小翠, 邹连慧. 基于多种群遗传算法的自动化立体库货位优化[J].吉林大学学报（工学版）, 2018,48(5): 1398-1404
JIAO Yu-ling, ZHANG Peng, TIAN Guang-dong, XING Xiao-cui, ZOU Lian-hui. Slotting optimization of automated warehouse based on multi-population GA[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1398-1404 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170691
Permissions

基于多种群遗传算法的自动化立体库货位优化

焦玉玲, 张鹏, 田广东, 邢小翠, 邹连慧

吉林大学交通学院,长春 130022

通信作者:田广东(1980-),男,副教授,博士.研究方向:物流系统工程.E-mail:tiangd2013@163.com

作者简介:焦玉玲(1968-),女,副教授,博士.研究方向:物流系统优化与设备自动化技术.E-mail:jyling777@163.com

基金:国家自然科学基金项目(51405075)

摘要

针对自动化立体仓库作业效率和安全性的要求,以货物出入库作业时间、货架整体等效重心和关联产品间相对聚集程度为目标函数,构建了多目标货位分配优化数学模型。将多目标模型加权归一化处理后,用简单加权遗传算法求解,为避免出现未成熟收敛问题,提出了多种群遗传算法求解货位分配优化数学模型,并结合玩具车组装和自动化立体库实验,求得自动化立体库货位分配结果并对比分析,验证了多种群遗传算法的有效性,为自动化立体库货位分配和优化提供了一种有效的解法。

关键词: 工业设计; 立体库货位分配; 多种群遗传算法; 多目标规划

中图分类号:TB491 文献标志码:A 文章编号:1671-5497(2018)05-1398-07

Slotting optimization of automated warehouse based on multi-population GA

JIAO Yu-ling, ZHANG Peng, TIAN Guang-dong, XING Xiao-cui, ZOU Lian-hui

College of Transportation, Jilin University, Changchun 130022,China

Abstract

To meet the requirement of the working performance and security of automated warehouse, the mathematical model of multi-objective slotting allocation optimization is constructed. The outbound-inbound operation time, the equivalent center of gravity of overall shelf and the degree of relative accumulation of related products are taken as the multi-objective functions. A Simple Weighted Genetic Algorithm (SWGA) is used to solve the model obtained by weighted and normalized multi-objective models. To avoid the problem of premature convergence, a Multi-population Genetic Algorithm (MPGA) is proposed to solve the optimization model of slotting allocation. Combined with experiment of toy car assembly and experiment of automated warehouse, the results of slotting allocation are obtained. The effectiveness of the MPGA is verified by comparison and analysis of the two results. This study provides an effective solution for automated warehouse slotting allocation and optimization.

Keyword: industriol design; warehouse slotting allocation; multi-population genetic algorithm; multi-objective planning

文章图片

0 引言

自动化立体库作为现代物流系统中的重要组成部分, 用立体库设备实现仓库高层货位合理化, 存取货物自动化, 操作控制简便化。货位分配的结果直接影响存取货物的自动化效率, 因此货位分配规划是自动化立体库管理的重要决策问题。张欢欢^[1]以货架的稳定性和出入库效率为目标, 建立货位分配数学模型, 采用简单加权遗传算法求解, 得到货位分配优化方案; Muppani等^[2]分析了货架上货物之间可能存在的相互联系, 结合存储空间成本和拣选作业成本, 构建了动态货位规划模型; 陈月婷等^[3]以货架稳定性和出入库效率为目标建立多目标货位分配优化数学模型, 运用改进粒子群算法求解模型; 陈厚松^[4]考虑货架的稳定性和货物存取效率作为目标建立数学模型, 运用简单加权遗传算法求解, 得到一组收敛的可行解; 郑雪梅^[5]构建数学模型考虑了货物出入库效率、货架稳定性和关联货物3个目标, 采用层次分析法确定目标权重, 并用遗传算法求解; 邓爱民等^[6]以货架稳定性、分巷道和出入库效率为目标建立多目标货位规划模型, 采用遗传算法求解; 张子才等^[7]以出入库效率和货物关联性原则建立多目标决策模型, 并运用仿真求解; 祖巧红等^[8]以作业效率和货架稳定性为目标建立货位分配模型, 采用简单加权遗传算法求解; 杨玮等^[9]以货架的稳定性和出入库效率为目标, 建立划分仓储区域和货位分配两阶段多目标优化模型。

研究货位规划问题时, 学者们多以货架的稳定性和货物出入库效率为目标构建货位分配模型, 多采用简单遗传算法求解, 易陷入局部最优, 出现未成熟收敛^[10]。本文以货架稳定性、作业效率和货物关联性为目标, 建立多目标货位规划模型, 用多种群遗传算法对规划模型求解, 验证了模型和算法的合理性。

1 模型建立

1.1 模型条件假设

建立货位分配模型时, 假设如下条件:

(1)货架上的货位大小尺寸相同。

(2)货物都是储存在托盘或货箱中, 货位能够放进托盘或货箱。

(3)堆垛机的水平和竖直方向以最大标定速度匀速运行, 不考虑加减速过程。

(4)堆垛机工作时间只考虑堆垛机运行到指定货位的时间, 堆垛机转向和拣选货物时间忽略不计。

(5)仓库内巷道载货出入口在同一侧。

(6)一个货位存储同一种类的货物, 且这个货位足够存储全部同种类货物。

(7)货架中的货位用二维坐标表示, 存储货物后, 货物的重心位于该货位的几何中心。

(8)只考虑货物重量, 不计货架重量。

1.2 货位分配数据

在流水线装配玩具车实验中, 生产节拍确定并分配作业元素到 6个工作站, 进行生产线平衡。假定产能1250台/天和每天工作时间8 h, 确定零配件的出库数量, 并将零配件分成了6大类。

1.3 建立多目标货位分配模型

根据玩具车模零配件属性、货架和堆垛机参数, 考虑自动化立体仓库货物出入库效率、货架的稳定性和关联货物空间就近存储的原则, 建立自动化立体库多目标货位分配模型。

(1)提高货物出入库效率

出入库效率以堆垛机单指令周期运行时间, 即所有零配件出入库所需时间最小作为目标:

$F_{1} (x, y) = \min [2 \times \overset{m}{\sum_{x = 1}} \overset{n}{\sum_{y = 1}} (D_{xy} \times t_{xy})] (1)$

$\begin{array}{l} t_{xy} = \max [(x - 0.5) \times \frac{L}{v_{x}}, (y - 0.5) \times \frac{H}{v_{y}}] (2) \\ D_{xy} = D'_{xy} \times p_{xy} (3) \end{array}$

式中: $x (x = 1, 2, \dots, m)$ 为货位沿货架长度方向的坐标单位; $y (y = 1, 2, \dots, n)$ 为货位沿货架高度方向的坐标单位; $m$ 为货架列数; $n$ 为货架层数; $L$ 为沿货架长度方向的一个货位长度; $H$ 为沿货架高度方向的一个货位高度; $v_{x}$ 为堆垛机水平速度; v_y为垂直运行速度; $t_{xy}$ 为堆垛机从货位运行到货架出入口的时间; $D_{xy}$ 为一个周期生产所需的货物总量; $D'_{xy}$ 为仓库中货位已存货物的总量; $p_{xy}$ 为一个周期出库的货物量占整个仓库存储量的比例。

(2)提高货架的稳定性

使整体货架等效重心的水平坐标尽可能接近货架水平方向的几何中心, 竖直方向坐标尽可能靠近最底层, 建立目标函数。

$\begin{array}{l} F_{2} (x, y) = \min |X_{g} - m \times \frac{L}{2}| (4) \\ F_{3} (x, y) = \min |Y_{g} - \frac{H}{2}| (5) \\ X_{g} = \frac{\overset{m}{\sum_{x = 1}} \overset{n}{\sum_{y = 1}} D_{xy} \times (x - 0.5) L}{\overset{m}{\sum_{x = 1}} \overset{n}{\sum_{y = 1}} D_{xy}} (6) \\ Y_{g} = \frac{\overset{m}{\sum_{x = 1}} \overset{n}{\sum_{y = 1}} D_{xy} \times (y - 0.5) H}{\overset{m}{\sum_{x = 1}} \overset{n}{\sum_{y = 1}} D_{xy}} (7) \\ s.t. \{\begin{array}{l} 0 \leq x \leq m \times L \\ 0 \leq y \leq n \times H \\ \overset{m}{\sum_{x = 1}} \overset{n}{\sum_{y = 1}} D'_{xy} \leq G_{\max} \end{array} (8) \end{array}$

式中:X_g为货架水平方向等效中心坐标; Y_g为竖直方向的等效中心坐标; $G_{\max}$ 为货架最大承载能力。

(3)关联性货物就近存储

用货物空间位置上的聚集程度表示货物之间的关联程度, 并以相对聚集程度最大为目标函数:

$\begin{array}{l} F_{4} (x, y) = \max (Dis / \overset{M}{\sum_{j = 1}} di s_{j}) (9) \\ di s_{j} = \\ \overset{M_{j}}{\sum_{i = 1}} \sqrt[]{(x_{ij} - {\bar{x}}_{j} {- 0.5)}^{2} + (y_{ij} - {\bar{y}}_{j} {- 0.5)}^{2}} (10) \\ Dis = \\ \overset{M}{\sum_{j = 1}} \overset{M_{j}}{\sum_{i = 1}} \sqrt[]{(x_{ij} {- \bar{x} - 0.5)}^{2} + (y_{ij} {- \bar{y} - 0.5)}^{2}} (11) \\ {\bar{x}}_{j} = \frac{1}{M_{j}} \overset{M_{j}}{\sum_{i = 1}} (x_{ij} - 0.5), {\bar{y}}_{j} = \frac{1}{M_{j}} \overset{M_{j}}{\sum_{i = 1}} (y_{ij} - 0.5) \\ \bar{x} = \frac{1}{M} \overset{M}{\sum_{j = 1}} {\bar{x}}_{j}, \bar{y} = \frac{1}{M} \overset{M}{\sum_{j = 1}} {\bar{y}}_{j} \end{array}$

式中: $M$ 为货物的大类数, 每大类包含 $M_{j}$ 种货物, $M_{j}$ 为同一种类货物数量; $di s_{j}$ 为同一种类货物之间的聚集程度; Dis为所有货物之间的聚集程度; $(x, y)$ 为货位坐标, $(x_{ij}, y_{ij})$ 为具有相互联系的货物的坐标, $({\bar{x}}_{j}, {\bar{y}}_{j})$ 为同一种类货物在货架上的等效坐标, $(\bar{x}, \bar{y})$ 为货物等效坐标。

1.4 目标函数归一化

多目标货位分配数学模型中, $F_{1} (x, y)$ 是最小出入库时间, 单位是s; $F_{2} (x, y)$ 和 $F_{3} (x, y)$ 货位的坐标取最小, 无量纲; $F_{4} (x, y)$ 是聚集程度最大, 无量纲。4个目标函数单位不一致, 需对多目标归一化处理。只需对 $F_{1} (x, y)$ 归一化, 取最大和最小两个确定的数值和参数λ , 归一化目标函数为:

$F'_{1} (x, y) = \frac{F_{1} (x, y) - \min F_{1} (x, y) + λ}{\max F_{1} (x, y) - \min F_{1} (x, y) + λ}$

目标函数量纲统一后, 对4个目标函数赋予不同权重 $ω_{i} (i = 1, 2, 3, 4),$ 并将多目标函数化为单目标函数:

$F (x, y) = \min [ω_{1} F'_{1} (x, y) + \overset{4}{\sum_{i = 2}} ω_{i} F_{i} (x, y)] (12)$

2 多种群遗传算法初始准备

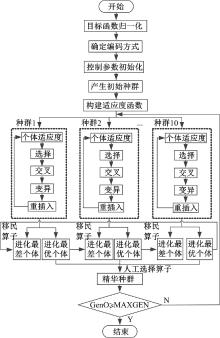
运用多种群遗传算法(Multi-population genetic algorithm, MPGA)求解货位分配模型时, 需做初始准备, 具体步骤如下。

(1)确定编码方式

根据货位分配目标函数和货架特点, 确定算法的编码方式为整数编码。一个染色体个体的编码代表一种可行的货位分配方案; 货架上的货位是由行数和列数两个维度确定的, 行数和列数分别用两位数表示, 种群中每个染色体个体的基因个数为4N个(N表示货物种类的数量); 每4个基因组成的编码代表当前货物在货架上的货位的坐标位置。

(2)控制参数初始化

控制参数有种群数量、代沟、交叉概率和变异概率及最优个体最少保持代数等。控制参数初始化是根据参数设计原则, 对控制参数赋初值。控制参数符号及初值见表1。

表1 多种群遗传算法控制参数赋值及其含义 Table 1 MPGA control parameter assignment and its meaning

参数	含义	初值
W_i	目标函数的权重(i=1, 2, 3, 4)	0.3, 0.3, 0.2, 0.2
$λ$	归一化参数	0.001
NIND	每个种群数量规模	100
M_P	种群数量	10
PRECI	货位对应的基因组数目	2
GGAP	遗传算法代沟	0.9
gen	各种群初始进化迭代计数器	0
genO	最优个体保持代数计数器	0
MAXGEN	最优个体最少保持代数	10
p_c	染色体个体间的交叉概率	0.7+(0.9-0.7)* rand(MP, 1)
p_m	染色体个体的变异概率	0.001+(0.003-0.001)* rand(MP, 1)

表1 多种群遗传算法控制参数赋值及其含义 Table 1 MPGA control parameter assignment and its meaning

(3)创造初始种群

在模型求解时, 遗传算法是从可行解集中搜索和进化获得最优解, 最初选取的一系列可行解就是算法中的初始种群。多种群遗传算法生成多个初始种群, 在多个子种群之间协同进化。根据表1确定的种群数量和群体规模参数, 结合染色体编码方式, 调用MATLAB遗传工具箱中的crtbp函数, 创建10个100行4N列的二维矩阵, 矩阵每一行代表一个染色体个体。

(4)构造适应度函数

算法中构造的适应度函数将影响可行解的收敛速度以及能否得到最优解^[11]。多种群遗传算法中各子种群在进化搜索过程中, 以种群中每个染色体个体对应的适应度函数为依据, 故适应度函数的复杂度决定了多种群遗传算法的复杂度。本文通过目标函数变换得到适应度函数:

$F (x, y) = \min [ω_{1} F'_{1} (x, y) + \overset{4}{\sum_{i = 2}} ω_{i} F_{i} (x, y)] (13)$

3 遗传操作设计

多种群遗传算法中最为关键的部分就是设计遗传操作, 包括选择操作、交叉操作、变异操作和重插入操作设计等。遗传操作设计如下:

(1)选择操作设计

根据每个染色体个体的适应度函数值进行选择, 适应度函数值较大的染色体个体被选中的可能性大, 即被选择的概率也较大, 选择操作避免进化过程中有用信息丢失, 提高全局收敛性和计算效率。常用轮盘赌选择^[11], 也叫比例选择。本文运用轮盘赌选择:选择染色体个体的适应度值较大的个体作为优选, 将该个体适应度值与种群中所有染色体个体的适应度值之和的比值作为种群中每个染色体个体被选中遗传给下一代的可能性概率。使种群中染色体个体的适应度函数值增加, 逐渐接近最优值。

(2)交叉操作设计

交叉操作是将两个相互配对的染色体按某种方式交换染色体上的部分基因, 产生新的染色体个体。多种群遗传算法中交叉操作设计就是确定交叉概率, 随机选取两个染色体个体交叉操作。不同的种群之间选取不同的交叉概率, 在确定了需要交叉操作的染色体个体后, 选择染色体个体基因交换的方式。常用的有单点交叉、两点交叉、均匀交叉和多点交叉等。本文采用改进的单点交叉操作。

(3)变异操作设计

变异操作设计选择较小的变异概率, 改变染色体个体某些位置上的基因值, 在种群中产生相类似的染色体个体, 提高算法的局部搜索能力。变异操作具有随机性, 但与选择和交叉操作结合, 能够避免丢失有用的信息, 保证算法的有效性。在多种群遗传算法中, 不同种群之间选择不同的变异概率进行操作。考虑问题的特殊性和货位坐标值的特点, 本文采取对调基因位的变异操作。

(4)重插入操作设计

重插入操作将新种群中适应度值大的染色体个体再次插入到原种群中, 代替原种群中适应度值小的染色体个体。多种群遗传算法为了保持种群规模在进化过程中不变以及种群染色体个体朝着特定的方向进化, 替换原种群中表现较差的染色体个体。

(5)移民操作设计

多种群遗传算法中的各子种群是相互独立进化的, 移民操作是通过移民算子在子种群之间的一种操作。移民算子操作将某个子种群中的适应度最小染色体个体用其他种群的适应度最大的染色体个体进行替代。移民操作增进了种群之间的信息交流, 实现了种群间的协同进化。

(6)进化终止判断

精华种群是保存着每次进化过程中最优的染色体个体的种群。通常采用精华种群中最优个体最少保持代数作为终止判断依据, 充分体现了遗传算法在进化过程中的知识积累。多种群遗传算法流程图见图1。

	Figure Option View Download New Window
	图1 多种群遗传算法流程图Fig.1 Flow chart of multi-population genetic algorithm

4 自动化立体仓库货位分配算例

4.1 自动化立体仓库实例

自动化立体库实验室配备高层立体货架、巷道式堆垛起重机、辊子输送机、入(出)库工作台和自动进(出)操作控制系统^[12]。货架存储区占地面积为4830 mm× 2800 mm, 货架高度为2420 mm, 两排牛腿式组合货架, 每排货架4层5列, 共40个货位, 货格尺寸为400 mm× 600 mm× 600 mm, 一个货格存储一个箱式托盘, 最大承重量为800 kg。配备一台巷道式堆垛起重机, 完成零配件的出入库作业, 堆垛机水平方向运行速度为v_x=1.2 m/s, 竖直方向运行速度v_y=1.0 m/s。

在自动化立体仓库中, 依据组装零配件的相关属性模拟入库操作。采用零配件出入库数量占比模拟零配件出入库频率, 零配件出入库数量占比是指出入库的零配件数量占整个仓库相应种类零配件存储数量的比值。仓库内根据所设定的安全库存确定所存储各种类的零配件数量。

4.2 自动化立体库求解条件

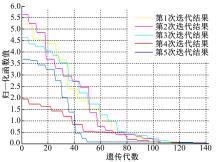
计算零配件的货位分配方案时, 假设堆垛机始终以恒定的速度在水平和竖直两个方向上运行, 即堆垛机运行时的启动时间、加速时间、减速时间、制动时间和拣选货物时间假定为零。零配件的出入库站台在同一端, 以出入库站台最近的货位作为坐标原点建立坐标系, 沿着货架长度方向设为 $x$ 轴, 沿着货架高度方向设为 $y$ 轴, $z$ 轴表示左、右两排货架(z=1时表示左边货架, z=2时表示右边货架)。

4.3 多种群遗传算法求解结果

结合自动化立体库实例模型, 运行MATLAB多种群遗传算法程序进化迭代, 结果见图2。表2为玩具车零配件的相关属性参数。

	Figure Option View Download New Window
	图2 归一化目标函数的MPGA迭代过程Fig.2 MPGA iterative process of normalized target function

表2 玩具车零配件的相关属性参数 Table 2 Relative property parameters of toy car parts

从图2可见, 货位分配数学模型的多目标归一化函数值随着进化总体趋势逐渐减小。在0~140范围内, 保持的进化代数(精华个体保持的代数)都小于事先设定的参数 MAXGEN; 进化代数大于140时, 随着进化代数的增加, 归一化目标函数曲线趋于水平, 直至最后精华个体保持代数等于MAXGEN时, 进化迭代终止, 输出精华个体作为最终结果。得到玩具车入库零配件的货位分配方案, 详见表2。如货物编号为1的零件名称车壳, 需求量为62.50 kg, 数量为1250个, 货位坐标为(3, 1, 1), 表示在货架上的第3行第1列, 并在巷道左侧(1表示在左侧货架上, 2表示在右侧货架上)。

5 结果对比与评价

5.1 目标函数值对比

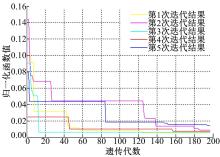
MPGA是对简单加权遗传算法(Simple weighted genetic algorithm, SWGA)的改进, 将单种群迭代进化全局搜索改进为多个种群协同进化全局搜索。现运用简单加权遗传算法和多种群遗传算法分别对零配件货位分配模型求解, 并比较目标函数值的结果, 见表3。

表3 MPGA和SWGA求解结果对比表 Table 3 Comparative function results of MPGA and SWGA

从3个目标函数值的两种算法结果可见:多种群遗传算法的结果优于简单加权遗传算法的结果; 出入库效率以单位秒表示, 数值越低效率越高; 货架整体稳定性以等效重心坐标(即横坐标)更加靠近货架几何中心(即横坐标2.5, 纵坐标接近第一层货架纵坐标0.5)稳定性好; 关联零配件之间聚集程度参数越大越好。

5.2 算法稳定性对比

运用简单加权遗传算法求解货位分配问题时, 采取了固定的遗传操作参数。在多种群遗传算法中, 每个子种群分别采用不同的遗传操作参数, 组合协同控制种群进化。两种算法分别重复运行5次, 得到两种算法的函数值变化趋势曲线, 分别见图2和图3。从两图对比可见:多种群遗传算法的收敛效率优于简单加权遗传算法。

	Figure Option View Download New Window
	图3 归一化目标函数的SWGA迭代过程Fig.3 SWGA iterative process of normalized target function

5.3 算法稳定性评价

运用稳定性系数sta评价两种算法稳定性, 稳定性系数sta是重复运行算法多次时, 最终结果相同的次数n与算法重复运行次数 $N$ 的比值。分别重复运行两种算法多次, 并汇总统计运算的结果中相同结果的个数, 并计算不同运算次数下两个算法的稳定性系数, 见表4。

表4 两种遗传算法运算结果统计 Table 4 Result statistics of operation for two GA

从表4的对比结果可见, 在重复运算相同次数的情况下, 多种群遗传算法的稳定性系数明显高于简单加权遗传算法, 从收敛效率和效果两个方面验证了多种群遗传算法的有效性。

6 结论

(1)对于自动化立体库的出入库效率、稳定性和关联零配件之间聚集程度3个目标函数值, 多种群遗传算法的结果都优于简单加权遗传算法。

(2)多种群遗传算法的稳定性和收敛速度都优于简单加权遗传算法。

(3)验证了多种群遗传算法求解货位分配多目标模型有效, 为自动化立体库货位分配和优化提供了一种有效的解法。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	张欢欢. 自动化立体库的若干关键技术与仿真[D]. 杭州: 浙江大学机械工程学院, 2008. Zhang Huan-huan. The key techniques and simulation of automated warehouse [D]. Hangzhou: College of Mechanical Engineering, College of Mechanical Engineering, , 2008. [本文引用:1]
[2]	Muppani V R, Adil G K. Efficient formation of storage classes for warehouse storage location assignment: a simulated annealing approach[J]. Omega, 2008, 36(4): 609-618. [本文引用:1]
[3]	陈月婷, 何芳. 基于改进粒子群算法的立体仓库货位分配优化[J]. 计算机工程与应用, 2008, 44(11): 229-231, 236. Chen Yue-ting, He Fang. The slotting allocation optimization of warehouse based on improved particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2008, 44(11): 229-231, 236. [本文引用:1]
[4]	陈厚松. 自动化立体库出入库货位分配优化研究[D]. 武汉: 武汉理工大学物流工程学院, 2011. Chen Hou-song. Research on outbound-inbound slotting allocation optimization of automated warehouse [D]. Wuhan: College of Logistics Engineering, College of Logistics Engineering, , 2011. [本文引用:1]
[5]	郑雪梅. S卷烟配送中心的货位优化研究[D]. 昆明: 昆明理工大学机电工程学院, 2013. Zheng Xue-mei. Study on location optimization of S cigarette distribution center [D]. Kunming: College of Mechanical and Electrical Engineering, College of Mechanical and Electrical Engineering, , 2013. [本文引用:1]
[6]	邓爱民, 蔡佳, 毛浪. 基于时间的自动化立体库货位优化模型研究[J]. 中国管理科学, 2013, 21(6): 107-112. Deng Ai-min, Cai Jia, Mao Lang. The optimization model of automated warehouse slotting allocation based on time[J]. China Scientific Management, 2013, 21(6): 107-112. [本文引用:1]
[7]	张子才, 李奎. 基于lingo算法的货位优化研究[J]. 宝钢技术, 2015(1): 1-4. Zhang Zi-cai, Li Kui. Study on slotting allocation optimization based on lingo algorithm[J]. Bao-steel Technology, 2015(1): 1-4. [本文引用:1]
[8]	祖巧红, 徐晓霞, 毛一超. 汽车零部件立体仓库货位优化问题研究[J]. 图学学报, 2015, 36(2): 312-317. Zu Qiao-hong, Xu Xiao-xia, Mao Yi-chao. Research on the optimization of automated warehouse slotting location for auto parts[J]. Journal of Graphics, 2015, 36(2): 312-317. [本文引用:1]
[9]	杨玮, 张文燕, 常晏彬, 等. 自动化立体库的货位分配优化[J]. 现代制造工程, 2014(12): 134-140. Yang Wei, Zhang Wen-yan, Chang Yan-bin, et al. The optimization of slotting allocation for automated warehouse[J]. Modern Manufacturing Engineering, 2014(12): 134-140. [本文引用:1]
[10]	吕卉, 周聪, 邹娟, 等. 基于多种群进化的遗传算法[J]. 计算机工程与应用, 2010, 28: 57-60. Lv Hui, Zhou Cong, Zou Juan, et al. The genetic algorithm based on multi-group evolution[J]. Computer Engineering and Applications, 2010, 28: 57-60. [本文引用:1]
[11]	雷英杰, 张善文, 李续武, 等. MATLAB遗传算法工具箱及其应用[M]. 西安: 西安电子科技大学出版社, 2005. [本文引用:2]
[12]	张鹏. 自动化立体库货位分配与Flexsim仿真研究[D]. 长春: 吉林大学交通学院, 2017. Zhang Peng. Research on the slotting allocation and Flexsim simulation of automated warehouse [D]. Changchun: College of Transportation, College of Transportation, 2017. [本文引用:1]

2008

0.0

... 张欢欢^[1]以货架的稳定性和出入库效率为目标,建立货位分配数学模型,采用简单加权遗传算法求解,得到货位分配优化方案 ...

2008

0.0

... Muppani等^[2]分析了货架上货物之间可能存在的相互联系,结合存储空间成本和拣选作业成本,构建了动态货位规划模型 ...

2008

0.0

... 陈月婷等^[3]以货架稳定性和出入库效率为目标建立多目标货位分配优化数学模型, 运用改进粒子群算法求解模型 ...

2011

0.0

... 陈厚松^[4]考虑货架的稳定性和货物存取效率作为目标建立数学模型,运用简单加权遗传算法求解,得到一组收敛的可行解 ...

2013

0.0

... 郑雪梅^[5]构建数学模型考虑了货物出入库效率、货架稳定性和关联货物3个目标,采用层次分析法确定目标权重,并用遗传算法求解 ...

2013

0.0

... 邓爱民等^[6]以货架稳定性、分巷道和出入库效率为目标建立多目标货位规划模型,采用遗传算法求解 ...

2015

0.0

... 张子才等^[7]以出入库效率和货物关联性原则建立多目标决策模型,并运用仿真求解 ...

2015

0.0

... 祖巧红等^[8]以作业效率和货架稳定性为目标建立货位分配模型,采用简单加权遗传算法求解 ...

2014

0.0

... 杨玮等^[9]以货架的稳定性和出入库效率为目标,建立划分仓储区域和货位分配两阶段多目标优化模型 ...

2010

0.0

... 研究货位规划问题时,学者们多以货架的稳定性和货物出入库效率为目标构建货位分配模型,多采用简单遗传算法求解,易陷入局部最优,出现未成熟收敛^[10] ...

2005

0.0

... 算法中构造的适应度函数将影响可行解的收敛速度以及能否得到最优解^[11] ...

... 常用轮盘赌选择^[11],也叫比例选择 ...

2017

0.0

... 1 自动化立体仓库实例自动化立体库实验室配备高层立体货架、巷道式堆垛起重机、辊子输送机、入(出)库工作台和自动进(出)操作控制系统^[12] ...