基于非线性动力学分析的车辆运行状态参数数据特征辨识

引用本文

刘兆惠, 王超, 吕文红, 管欣. 基于非线性动力学分析的车辆运行状态参数数据特征辨识[J].吉林大学学报（工学版）, 2018,48(5): 1405-1410
LIU Zhao-hui, WANG Chao, LYU Wen-hong, GUAN Xin. Identification of data characteristics of vehicle running status parameters by nonlinear dynamic analysis[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1405-1410 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20180330
Permissions

基于非线性动力学分析的车辆运行状态参数数据特征辨识

刘兆惠¹, 王超¹, 吕文红¹, 管欣²

1.山东科技大学交通学院,山东青岛 266590

2.吉林大学汽车仿真与控制国家重点实验室,长春 130022

作者简介:刘兆惠(1972-),女,副教授,博士.研究方向:交通安全技术.E-mail:liuzhaohuijlu@126.com

基金:国家自然科学基金重大项目(91120306/F03)

摘要

考虑到车辆运行状态参数时间序列不仅呈现随机性,有些还呈现混沌特性,因此,有必要对其参数数据特征进行正确辨识,以区分其参数时间序列是随机的还是混沌的。应用延迟坐标状态空间重构和最大李雅普诺夫(Lyapunov)指数法进行了非线性动力学分析,对车辆运行状态参数数据的有效信息进行深层提取。研究结果表明,由G-P算法求解得到的饱和关联维数是非整数,且最大Lyapunov指数大于零,两者综合表征此序列是混沌时间序列。因此,依据辨识结果选择适宜方法进行后继研究更具科学性。

关键词: 交通运输系统工程; 数据特征辨识; 非线性动力学; 车辆运行状态参数; 延迟坐标状态空间重构; 关联维数; 最大李雅普诺夫(Lyapunov)指数

中图分类号:U492.8 文献标志码:A 文章编号:1671-5497(2018)05-1405-06

Identification of data characteristics of vehicle running status parameters by nonlinear dynamic analysis

LIU Zhao-hui¹, WANG Chao¹, LYU Wen-hong¹, GUAN Xin²

1.College of Transportation, Shandong University of Science and Technology, Qingdao 266590, China

2.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

Abstract

Time series of vehicle running status parameters not only present randomness, but also present chaotic characteristics. Therefore it is necessary to accurately identify the data characteristics of vehicle running status parameters, in order to identify if its parameter time series is random or chaotic. To obtain the maximum availed data information of the vehicle running status parameters. Delay-coordinate space reconstruction and the largest Lyapunov exponent method were used to carry out nonlinear dynamic analysis. Speed time series is used as an example, the results show that based on the Delay-coordinate phase space reconstruction, the saturate correlation dimension obtained by G-P algorithm is not an integer, and the Max-Lyapunov exponent is grater than zero, which demonstrate speed time series is chaotic time series from two aspects. Thus, data characteristics of the vehicle running status parameters can be identified by nonlinear dynamic analysis, and then appropriate methods can be used in follow-up research based on the identification, which is more scientific.

Keyword: engineering of communications and transportation system; data characteristics identification; non-linear dynamics; vehicle running status parameter; delay-coordinate phase space reconstruction; correlation dimension; max-Lyapunov exponent

文章图片

0 引言

国内外研究人员对于车辆安全预警系统已开展了一系列相关研究, 该领域已有的研究成果主要包括:驾驶员状态监控系统(DCWS)^[1]、车道偏离预警系统(LDWS)^[2]、碰撞预警/避免系统(CW/CA)^{[3, 4]}、车辆侧翻预警系统(ARCS)^[5]、自适应巡航控制系统(ACC)^[6]及视觉增强系统(VE)^[7]等。其中, 通过车辆运行状态参数分析进行预警研究的成果主要包括:Lund等^[8]对临界侧滑速度(CSV)指标进行了研究, 将能够引起车辆侧翻的最小侧滑速度作为侧翻阈值; Yoon等^[9]采用基于传感器信号静态阈值的控制方法, 当车辆的侧向加速度、侧倾角等稳定性参数超过预定的阈值时, 系统自动控制执行器发出警示信息来警告驾驶员; 毕胜强等^[10]借助驾驶模拟器采集数据, 建立了面向驾驶行为预警的基于支持向量机(SVM)的换道意图辨识模型; 高振海等^[11]研究了人-车-路环境下无意识车道偏离识别方法, 通过实车实验分析相关参数, 采用高斯混合隐马尔科夫(GM-HMM)构建识别模型, 较好地提高了车道偏离预警的工作效能。

与现有研究的切入点不同, 本文考虑通过车辆运行状态参数进行道路交通事故预警研究的前提是数据有效信息的深层提取。由于分析观测时间序列的演化规律是分析系统动力学行为的重要手段之一, 且准确分析试验数据也是获得正确预测结果的关键所在, 基于上述原因, 选择车辆运行状态参数时间序列作为研究对象, 考虑到车辆运行状态任一参数时间序列中不仅包含了系统变量的所有信息, 而且也包含了参与系统演化的其他变量的信息, 从而使时间序列不仅仅呈现随机性, 有些还呈现混沌特性, 因此, 预测车辆运行状态就不能仅仅因循传统的程序与方法, 而应先辨识其参数时间序列是随机的还是混沌的, 在此辨识基础上确定相应的预测方法, 最终达到精确预警的目的。

为深入分析时间序列的动力学机制, Packard等^[12]提出了延迟坐标状态空间重构方法, Takens定理证明了当嵌入维数m≥ 2D+1(D为吸引子的维数), 则在此重构的相空间中可以恢复出系统原有的规律, 且保持微分同胚。从而, 在重构相空间中, 时间延迟和嵌入维数的确定具有十分重要的意义。

在重构相空间的基础上, 考虑到关联维和最大Lyapunov指数是表征系统混沌性的两个重要特征量^{[13, 14]}, 在获得关联维的基础上, 进一步求解最大Lyapunov指数, 从两个方面相互印证, 对车辆运行状态参数时间序列进行数据特征辨识。

1 确定重构相空间的延迟时间τ

对于实际中获取的时间序列{x_i, i=1, 2, ..., N}, 采用成熟的自相关函数法求τ 。自相关函数可表示为:

$R_{xx} (jτ) = \frac{1}{N} \overset{N - 1}{\sum_{i = 0}} x_{i} x_{i + jτ} (1)$

式中:x_i和x_i+jτ 表示时段为jτ 的不同时点所对应的值; R_xx(jτ )为两时点(i和j+jτ )运动的相关程度; 保持j不变, 可得R_xx(jτ )关于时间τ (τ =1, 2, ...)的函数图像。

当 $R_{xx} (jτ)$ 下降至初值的1-1/e时, 相应横坐标数值即为所求的最佳延迟时间。

2 确定重构相空间的嵌入维数m

现有研究结果已证明, 饱和关联维数可作为吸引子维数的近似, 同时考虑到Takens定理中嵌入维数和吸引子维数的关系, 以计算饱和关联维数的G-P算法^[15]作为桥梁, 确定m。

设定初值m₀, 由m₀和τ , 基于单变量时间序列{x_i, i=1, 2, …, N}支起一个嵌入空间:

$\begin{array}{l} Y (t_{i}) = [x (t_{i}), x (t_{i} + τ), x (t_{i} + 2 τ), \dots, \\ x (t_{i} + (m_{0} - 1) τ] (2) \end{array}$

式中:t_i=1, 2, …, M; M=N-(m₀-1)Y(t_i)τ 。

此m₀维相空间中任意两个相点 $Y (t_{i}) 和 Y (t_{j})$ 之间的距离可定义为:

$| Y (t_{i}) - Y (t_{j}) | = \max_{1 \leq l \leq m} | Y (t_{il}) - Y (t_{jl}) | (3)$

式中:i≠ j; Y(t_il)和Y(t_jl)分别为两个相点Y(t_i)和Y(t_j)的分量。

计算关联函数C(r):

$C (r) = \lim_{M \to \infty} \frac{1}{M^{2}} \overset{M}{\sum_{i, j = 1}} θ (r - | Y (t_{i}) - Y (t_{j}) |) (4)$

式中: $r$ 为给定的临界距离; $θ$ 为Heaviside单位函数; $C (r)$ 为相空间中距离小于 $r$ 的相点对数在M²种配对中所占的比例。

$θ (x) = \{\begin{array}{l} 0, x \leq 0 \\ 1, x > 0 \end{array} (5)$

关联函数 $C (r) 在 r \to 0 时与 r$ 存在以下关系:

$\lim_{r \to 0} C (r) \propto r^{d} (6)$

式中: $d$ 为关联维数。

随着 $r$ 值的变化, $C (r)$ 有如下标度律:

$d (m) = \frac{\ln C (r)}{\ln r} (7)$

从而 $m_{0}$ 维相空间的关联维数 $d (m_{0})$ 可求。

将嵌入维数递增, 计算式(2)~(7)。随着嵌入维数的增大, 若 $\ln C (r) ⁃ \ln r$ 曲线斜率趋于一个饱和值, 则表明系统存在混沌, 且此饱和值即为饱和关联维数d。因此, 可以根据关联维数是否具有饱和现象来区分混沌与随机序列。由文献[13, 14]可知, 若饱和关联维数d为非整数, 则更进一步证明此时间序列为混沌时间序列, 饱和关联维数d对应的m即为所求嵌入维数。

综上, 可得延迟坐标状态空间为:

$\begin{array}{l} Y (t_{i}) = [x (t_{i}), x (t_{i} + τ), x (t_{i} + 2 τ), \\ \dots, x (t_{i} + (m - 1) τ] (8) \end{array}$

3 最大Lyapunov指数λ ₁的求解

格里波基在1983年已证明只要最大Lyapunov指数大于零, 就可以肯定混沌的存在^[16]。为此, 本文采用计算精度较高、且可直接计算最大Lyapunov指数λ ₁的方法— — 小数据量法^[17]进行求解。具体过程如下:

计算重构空间中相点Y_j与邻近点 $Y_{\hat{j}}$ 的距离, 保证参考点Y_j与邻近点 $Y_{\hat{j}}$ 位于不同轨线, 确定最近邻近点对的初始距离d_j(0)为:

$d_{j} (0) = \min_{\hat{j}} ‖ Y_{j} - Y_{\hat{j}} ‖, | j - \hat{j} | > p (9)$

式中: $p$ 为平均周期, 由FFT变换可得; $| j - \hat{j} | > p$ 表示将邻近点对限制在不同轨线上。

计算相空间中第j对最近邻近点对经过i个离散时间步长后的距离d_j(i):

$\begin{array}{l} d_{j} (i) = | Y_{j + i} - Y_{\hat{j} + i} | (10) \\ i = 1, 2, \dots, \min (M - j, M - \hat{j}) \end{array}$

对每个i, 求出所有j的ln d_j(i)平均值y(i), 即测量平均分离。

$y (i) = \frac{1}{q Δ t} \overset{q}{\sum_{j = 1}} \ln d_{j} (i) (11)$

式中:q为非零d_j(j)的数目; Δ t为样本周期。

上述曲线拟合直线的斜率即为所求的最大Lyapunov指数λ ₁。

4 算例分析

4.1 数据采集及去噪

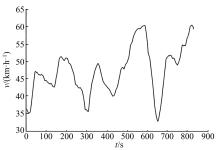
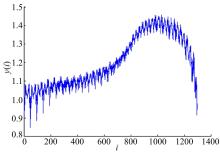
为获取准确的车辆运行状态参数时间序列数据, 通过实车试验进行数据采集^[18]。实车试验中采用ToCeiL非接触式测速仪和时间信号发生器测定车速、纵向加速度和时间; 采用微型航姿参考系统测量车辆侧倾角; 采用QCW-1A汽车操纵稳定性测试仪和WS-U60232/C型数据采集仪获取横向加速度数据。本文仅以车辆速度为例进行说明。图1为试验路段车辆速度时间序列图形, 试验采样间隔时间为1 s, 采集样本量为1642个, 采样时间为821 s。图2为经过小波软阈值去噪后的车辆速度时间序列图形。

	Figure Option View Download New Window
	图1 车辆速度时间序列Fig.1 Vehicle speed time series

	Figure Option View Download New Window
	图2 经小波去噪后的车辆速度时间序列Fig.2 Vehicle speed time series after wavelet de-noising

4.2 延迟坐标状态空间重构

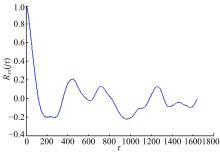
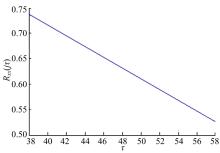
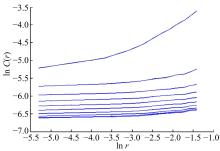
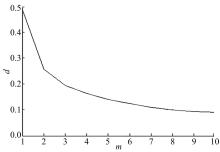
利用Matlab编程, 由式(1)可得到车辆速度时间序列的自相关函数曲线和最佳延迟时间分别如图3和图4所示, 其中, 横坐标为延迟时间τ , 纵坐标为自相关函数R_xx(jτ )。根据本文第1节可知, 当R_xx(jτ )下降至初值的1-1/e时, 相应横坐标数值即为所求的最佳延迟时间τ , 从图4中可求得τ =48。利用采集到的车速序列, 先给定一个较小嵌入维数值m₀(一般取1), 根据式(2)得到车辆速度时间序列的一个重构相空间。按照式(3)~(7), 将相空间嵌入维数m由小增大, 得到车辆速度时间序列lnC(r)-lnr双对数关系曲线, 如图5所示。从图5可以看出, 随着 $m$ 的增加, 曲线变得越来越密, 当m≥ 8, 斜率趋于一个饱和值, 即d(8)=d(9)=d(10)=…。因此, m=8就是所求嵌入维数, 对应的曲线斜率就是饱和关联维数。为了更加直观地看出关联维数 $d 和嵌入维数 m 之间的关系, 给出 d⁃m$ 关系图(见图6), 横坐标为嵌入维数m, 纵坐标为关联维数d。由图6可以看出, 对应嵌入维数m=8, 饱和关联维数d=0.1。根据第2节可知, 关联维数趋于饱和, 且所求饱和关联维数为非整数, 证明此序列是混沌时间序列。为了进一步印证, 需计算识别序列混沌性的另一个特征量最大Lyapunov指数。

	Figure Option View Download New Window
	图3 车速时间序列的自相关函数曲线图Fig.3 Self-correlation function graph of vehicle speed time series

	Figure Option View Download New Window
	图4 确定最佳延迟时间Fig.4 Confirming optimal delay time

	Figure Option View Download New Window
	图5 车速时间序列lnC(r)-lnr双对数关系曲线图Fig.5 lnC(r)-lnr relations map of vehicle speed time series

	Figure Option View Download New Window
	图6 车速时间序列重构相空间的d-m关系图Fig.6 d-m relations of reconstructed phase space of vehicle speed time series

4.3 数据特征的最大Lyapunov指数分析

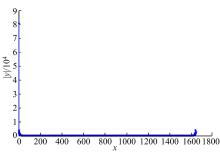
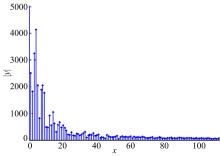
为了确定平均周期P, 需对车辆速度时间序列进行FFT变换, 结果如图7所示, 其横坐标为采样频率为2 次/s的样本数, 纵坐标为车辆速度经FFT变换后的幅值。将图7局部放大, 得到图8, 由峰值可以看出P=4。

	Figure Option View Download New Window
	图7 车速时间序列FFT变换Fig.7 FFT transform of vehicle speed time series

	Figure Option View Download New Window
	图8 平均周期P的确定Fig.8 Determination of average cycle P

在延迟坐标状态空间重构的基础上(见式(8)), 根据式(9)~(11)计算最近邻近点对的平均分离, 结果如图9所示, 其横坐标为邻近点对的离散时间步数i, 纵坐标为平均值y(i)。用最小二乘法进行直线拟合, 直线斜率即为最大Lyapunov指数λ ₁, 可得λ ₁=0.0003> 0, 表明该车辆速度时间序列存在混沌现象。由最大Lyapunov指数大于零, 结合4.2节中G-P算法求解的饱和关联维数 $d$ 为非整数, 两者综合表征此序列是混沌时间序列。

	Figure Option View Download New Window
	图9 车辆速度时间序列的最大Lyapunov指数Fig.9 Largest Lyapunov exponent of vehicle speed time series

5 结论

(1)与现有事故预警文献中车辆运行状态研究的切入点不同, 考虑到车辆运行状态任一参数时间序列中均隐含相关因素的大量信息, 从而使其时间序列不仅仅呈现随机性, 有些还呈现混沌特性。因此, 采用非线性动力学分析进行车辆运行状态参数数据有效信息的深层提取, 以辨识其数据特征, 明确其参数时间序列是随机的还是混沌的。从而为后继研究中选择适宜预测方法, 进而实现精确预警奠定前期基础。

(2)采用延迟坐标状态空间重构法, 在确定性的基础上, 对序列动力学因素进行分析, 对影响相空间重构的关键参数— — 嵌入维数和延迟时间进行求解。通过Takens定理和G-P算法确定饱和关联维数, 进而确定嵌入维数m, 根据自相关函数下降到初始值的1-1/e时确定最佳延迟时间τ , 从而将在低维空间中貌似杂乱无序的车辆运行状态参数时间序列纳入某种可描述的框架之下。

(3)考虑到关联维数和最大Lyapunov指数是系统混沌性的两个重要表征量, 在已获得关联维的基础上, 采用小数据量算法求解最大Lyapunov指数, 进而从两个方面综合印证, 对车辆运行状态参数时间序列进行数据特征辨识。

(4)在实车试验的基础上, 以车速为例说明车辆运行状态参数时间序列的非线性动力学分析过程, 从而为车辆运行状态参数分析提供一种新的思路和方法。实例分析结果表明:通过延迟坐标状态空间重构, 根据G-P算法求解得到的饱和关联维数d_饱和=0.1是非整数, 且最大Lyapunov指数大于零, 两者综合表征此序列是混沌时间序列, 应采用非线性动力学中的混沌理论进行后继研究。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Bell J L, Taylor M A, Chen G, et al. Evaluation of an in-vehicle monitoring system (IVMS) to reduce risky driving behaviors in commercial drivers: comparison of in-cab warning lights and supervisory coaching with videos of driving behavio[J]. Journal of Safety Research, 2017, 60(5): 125-136. [本文引用:1]
[2]	Risack R, Mohler N, Enkelmann W. A video-based lane keeping assistant[C]∥IEEE Intelligent Vehicles Symposium, IEEE, 2000: 356-361. [本文引用:1]
[3]	Shrestha R. Estimation of vehicle lateral position using the optical flow method[D]. USA: Polytechnic College, Polytechnic College, 2013. [本文引用:1]
[4]	Yadav G K, Kancharla T, Nair S. Real time vehicle detection for rear and Forward collision warning systems[C]∥Advances in Computing and Communications, Kochi, India, 2011: 368-377. [本文引用:1]
[5]	Han I, Rho K. Characteristic analysis of vehicle rollover accidents: rollover scenarios and prediction/warning[J]. International Journal of Automotive Technology, 2017, 18(2): 451-461. [本文引用:1]
[6]	Eskand arian A. Hand book of Intelligent Vehicles[M]. New York: Springer, 2012: 975-996. [本文引用:1]
[7]	Dabbour Essam Mohamed S A E A. Development of in-vehicle collision warning system for intersections[D]. Canada: School of Engineering Architecture and Science, School of Engineering Architecture and Science, 2010. [本文引用:1]
[8]	Lund Y I, Bernard J E. Analysis of simple rollover metrics[C]∥SAE Paper, 950306. [本文引用:1]
[9]	Yoon J, Kim D, Yi K. Design of a rollover index-based vehicle stability control scheme[J]. Vehicle System Dynamics, 2007, 45(5): 459-475. [本文引用:1]
[10]	毕胜强, 梅德纯, 刘志强, 等. 面向驾驶行为预警的换道意图辨识模型研究[J]. 中国安全科学学报, 2016, 26(2): 91-95. Bi Sheng-qiang, Mei De-chun, Liu Zhi-qiang, et al. Research on lane change intention identification model for driving behavior warning[J]. China Safety Science Journal, 2016, 26(2): 91-95. [本文引用:1]
[11]	高振海, Le DinhDat, 胡宏宇, 等. 驾驶员无意识车道偏离识别方法[J]. 吉林大学学报: 工学版, 2017, 47(3): 709-716. Gao Zhen-hai, Le DinhDat, Hu Hong-yu, et al. Recognition method of driver's unintentional lane departure[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(3): 709-716. [本文引用:1]
[12]	Packard N H, Crutchfield J P, Farmer J D, et al. Geometry from a time series[J]. Phys Rev Lett, 1980, 45: 712-716. [本文引用:1]
[13]	吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2002. [本文引用:1]
[14]	黄润生. 混沌及其应用[M]. 武汉: 武汉大学出版社, 2000. [本文引用:1]
[15]	Grassberger P, Procaccia I. Measuring the strangeness of strange attractors[J]. Physics D, 1983, 9(1): 189-208. [本文引用:1]
[16]	Grebogi C, Ott E, Yorke J A. Crises, sudden changes in chaotic attractors, and transients chaotic[J]. Physica D, 1983, 7: 181-200. [本文引用:1]
[17]	Rosenstein M T, Collins J J, de Luca G J. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physics D, 1993, 65(6): 117-134. [本文引用:1]
[18]	刘兆惠. 复杂交通路况下车辆运行状态预测方法研究[R]. 长春: 汽车仿真与控制国家重点实验室博士后研究工作报告, 2015. Liu Zhao-hui. A study on prediction methods of vehicle status in complex transportation environment[R]. Changchun: Post-doctoral Report of State Key Laboratory of Automotive Simulation and Control, 2015. [本文引用:1]

2017

0.0

... 0 引言国内外研究人员对于车辆安全预警系统已开展了一系列相关研究,该领域已有的研究成果主要包括:驾驶员状态监控系统(DCWS)^[1]、车道偏离预警系统(LDWS)^[2]、碰撞预警/避免系统(CW/CA)^[3,4]、车辆侧翻预警系统(ARCS)^[5]、自适应巡航控制系统(ACC)^[6]及视觉增强系统(VE)^[7]等 ...

2000

0.0

2013

0.0

2011

0.0

2017

0.0

2012

0.0

2010

0.0

... 其中,通过车辆运行状态参数分析进行预警研究的成果主要包括:Lund等^[8]对临界侧滑速度(CSV)指标进行了研究,将能够引起车辆侧翻的最小侧滑速度作为侧翻阈值 ...

2007

0.0

... Yoon等^[9]采用基于传感器信号静态阈值的控制方法,当车辆的侧向加速度、侧倾角等稳定性参数超过预定的阈值时,系统自动控制执行器发出警示信息来警告驾驶员 ...

2016

0.0

... 毕胜强等^[10]借助驾驶模拟器采集数据,建立了面向驾驶行为预警的基于支持向量机(SVM)的换道意图辨识模型 ...

2017

0.0

... 高振海等^[11]研究了人-车-路环境下无意识车道偏离识别方法,通过实车实验分析相关参数,采用高斯混合隐马尔科夫(GM-HMM)构建识别模型,较好地提高了车道偏离预警的工作效能 ...

1980

0.0

... 为深入分析时间序列的动力学机制,Packard等^[12]提出了延迟坐标状态空间重构方法,Takens定理证明了当嵌入维数m#cod#x02265 ...

2002

0.0

... 在重构相空间的基础上,考虑到关联维和最大Lyapunov指数是表征系统混沌性的两个重要特征量^[13,14],在获得关联维的基础上,进一步求解最大Lyapunov指数,从两个方面相互印证,对车辆运行状态参数时间序列进行数据特征辨识 ...

2000

0.0

1983

0.0

... 2 确定重构相空间的嵌入维数m现有研究结果已证明,饱和关联维数可作为吸引子维数的近似,同时考虑到Takens定理中嵌入维数和吸引子维数的关系,以计算饱和关联维数的G-P算法^[15]作为桥梁,确定m ...

1983

0.0

... ₁的求解格里波基在1983年已证明只要最大Lyapunov指数大于零,就可以肯定混沌的存在^[16] ...

1993

0.0

... 小数据量法^[17]进行求解 ...

2015

0.0

... 1 数据采集及去噪为获取准确的车辆运行状态参数时间序列数据,通过实车试验进行数据采集^[18] ...