Peck^[3]第一次全面地揭示出了地层损失的定义及预测隧道因开挖而导致的地表沉降的途径。他认为地层的损失导致地表的沉降, 并设想土体不会排水, 地表沉降槽的体积与土体损失的体积相同。同时, 揭示出了沿水平方向沉降槽近似正态分布的理念, 即Peck曲线:

S(x)=Smaxexp[-x22i2](1)Smax=πR2ηi2π(2)i=z2πtan45°-φ/2(3)

式中: x为隧道某一断面上任意一点与隧道轴线方向间的水平距离; i为地面沉降槽的宽度系数; Smax为轴线上方地表沉降的最大值; S(x)为 x处相对应地表沉降; R为隧道掘进半径; η为地层的损失率; z为隧道轴心埋深; φ为土体内摩擦角均值。

马可栓^[7]利用Peck单线公式, 依次计算了因先行、后行隧道掘进所导致的地面沉降值, 同时赋予先行、后行隧道的 i和 η以相异值, 通过叠加的方法, 计算出了双线隧道的沉降总值:

S(x)=Smax, fexp-(x-0.5L)22if2+Smax, lexp-(x+0.5L)22il2(4)

式中: Smax, f=πR2ηfif2π; Smax, l=πR2ηlil2π; if、il分别为先行、后行隧道的地表沉降槽宽度系数; ηf、ηl分别为先行、后行隧道的地层损失率; L为隧道轴间距。

通过对单线Peck公式(1)~(3)的观察可知: S(x)为 x~N(x, i)的概率密度函数与系数 πR2η的乘积, 即 S(x)=S(x, i, η)=πR2η·F(x, i); η可视作沉降曲线的放大、缩小因子, 对沉降曲线的形状变化趋势不产生任何影响; i与高斯曲线的标准差相对应, 对沉降曲线的形态产生影响。对于双线Peck公式(4), S(x)中的 ηf、ηl控制着先行、后行隧道沉降曲线的整体轮廓; if、il控制着先行、后行隧道沉降曲线的具体形状; L与高斯曲线的均值相对应, 对沉降曲线的双峰位置产生影响。

根据第1节的讨论, 可知系数 πR2η不影响沉降槽宽度影响范围, 但影响着沉降曲线垂直方向的变形。为更好地研究沉降槽有效宽度范围, 对系数 πR2η予以略去, 同时对先行、后行隧道的沉降槽宽度系数及土体损失率的不同所带来的影响予以忽略, 假设 if=il, ηf=ηl,即 X~N(L/2, i2)。进一步化为标准正态分布: Z=(X-L/2)/i~N(0, 1)。

通过对不同置信率(0.99、0.95、0.9)对应的置信区间进行计算, 换算出沉降槽的有效宽度范围, 结果如表1所示。

表1

Table 1

表1(Table 1)

表1 不同置信率下的沉降槽有效宽度范围 Table 1 Effective width of settling tank under different confidence rates 置信率 沉降槽有效宽度范围 0.99 (-L/2-2.8i, L/2+2.8i) 0.95 (-L/2-2.24i, L/2+2.24i) 0.90 (-L/2-1.96i, L/2+1.96i)

表1 不同置信率下的沉降槽有效宽度范围 Table 1 Effective width of settling tank under different confidence rates

0.9的置信率常常被应用于实际工程当中, 且与之相应的隧道沉降槽的有效宽度大致为 L+4i。在 L+4i区间以内, 用作施工监测的沉降测点需提前设置好, 但对于此区间以外的区域, 地表沉降近乎不计, 所以不必设置测点。

陈春来等^[8]提出:双线盾构隧道掘进施工过程当中, 地表沉降曲线的外形随隧道轴间距 L的变化而变化, 即: L逐步增大时, 沉降曲线由V型转变为W型。上述结论是在沉降槽宽度系数 i恒定的基础之上得出的。

通过前面的讨论得知:沉降槽的宽度系数 i、隧道的轴间距 L是影响沉降曲线形状的首要原因。假定 C=L/i(i> 0),随着 C从0慢慢增大, 沉降曲线的外形也由V型变为W型。例如:当 C=0时, 双线隧道沉降曲线可视作左、右单线隧道沉降曲线的叠加, S(x)双=2S(x)单,此种情况下沉降曲线呈V型。因此, 可通过C的变化来判定沉降曲线的形态, 并将其定义为双线盾构隧道地表沉降形态变化系数。

采用枚举法, 在不同 C值的基础上绘制得到相对应的地表沉降曲线图, 通过对比分析依次探究:当 L不变、 i变化时以及当 i不变、 L变化时双线盾构隧道地表沉降曲线随 C值变化的规律。

(1) L不变, i变化

令η =0.5%, L=14 m。 C依次为1、1.9、2、2.1、3、6、6.9、7、7.1时, 与之相应的 i依次为14、7.37、7、6.67、4.67、2.33、2.03、2、1.97, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 L不变, i变化时双线Peck公式沉降曲线形状Fig.1 Two-line Peck formula settling curve shape when i varying with constant L

(2) i不变, L变化

令η =0.5%, i=7。C依次为1、1.9、2、2.1、3、6、6.9、7、7.1时, 与之相应的 L依次为7、13.3、14、14.7、21、42、48.3、49、49.7, 如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
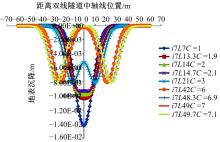	图2 i不变, L变化时双线Peck公式沉降曲线形状Fig.2 Two-line Peck formula settling curve shape when L varying with constant i

由图1、图2可知:当 C逐步递增时, 沉降曲线的外形也随之从V型变为W型, 进而变为彼此互不相干的两个V型。双线盾构隧道地表沉降曲线的形状由“ 单峰” 变为“ 双峰” 时, 对应的临界点系数为C=2, 而由“ 双峰” 变成相互独立的两个“ 单峰” 时, 对应的临界点系数则为C=7。

在 L不变、 i变化的情况下, 当 C逐步增大时, 沉降曲线的形状从平缓变为陡峭, 与之相应的沉降量的最大值随之变大, 同时“ 双峰” 变得越来越窄。“ 单峰” 时, 沉降量的最大值出现在双线隧道中心轴上; 变为“ 双峰” 后, 则在对应的左、右线隧道各自的隧道轴心处显现。

在 i不变、 L变化的情况下, 当 C逐步增大时沉降曲线的形状从陡峭变为平缓, 与之相应的沉降量的最大值随之变小, “ 双峰” 的宽度恒定, 两峰之间的距离增大。

3.1.1 工程基本概况

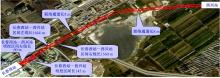
如图3所示, 长春西站→ 西兴站盾构区间:自长春西站向东北方向铺设, 止于西兴站。对于此段区间隧道, 其大部分都位于地下水位较高的空旷区域内, 且穿越的土层以粉质黏土、全风化泥岩和强风化泥岩为主。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 盾构区间平面示意图Fig.3 Sketch map of shield interval plane

3.1.2 地表沉降监测

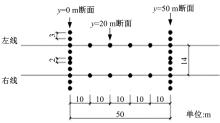
隧道开挖过程中, 通过持续或周期性地对相应隧道断面的地表沉降监测点进行监测, 确定沉降监测点的沉降量及变化趋势, 用以分析隧道开挖过程中导致的地表最终沉降量。监测点需在施工开始前设置:从竖井端部端面开始, 沿长春西站→ 西兴站方向, 间隔50 m设置一大断面, 间隔10 m设置一小断面, 如图4所示。利用GPS定向技术保证监测点断面与隧道断面彼此相对应。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 地表沉降监测点位示意图Fig.4 Sketch map of surface subsidence monitoring site

通过MIDAS/GTS NX有限元软件建立模型:土体运用实体单元, 盾构隧道盾壳、管片运用板单元, 均视作弹性材料。材料相应的具体参数见表2。

表2

Table 2

表2(Table 2)

表2 材料参数表 Table 2 Material physical and mechanical parameters 材料 重度 /(kN∙ m-3) 弹性模量 /MPa 泊松 比 黏聚力 /kPa 内摩擦角 /(° ) 粉质黏土1 20 10 0.25 30 12.5 粉质黏土2 20 14 0.2 45 14.7 全风化泥岩 20.6 50 0.2 56 15 强风化泥岩 21.7 170 0.2 80 20 盾壳 78.5 200 000 0.3 管片 24.5 27 600 0.2 注浆 24 20 000 0.2

表2 材料参数表 Table 2 Material physical and mechanical parameters

图5为盾构隧道网格模型示意图。模型按80 m× 60 m× 40 m尺寸建立, 埋入深度h=13.4 m, 盾构隧道的外径R=3 m, 左右线的轴间距d=14 m。隧道左右线采取先后开挖法:左线率先开挖, 当左线开挖到60 m时, 右线进行掘进。管片按每环2 m采用, 每步掘进4 m, 隧道左线率先掘进15步, 以此来模拟单线开挖步骤; 右线在其后掘进15步, 以此来模拟双线间的彼此干扰现象, 左右线合计为30步。此隧道开挖步骤模拟如下:

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 盾构隧道网格模型示意图Fig.5 Shield tunnel grid model

(1)将土体激活, 将位移约束、自重荷载施加其上, 后将位移清零。

(2)进行掘进模拟, 将每步的土体进行钝化, 然后将开挖压力施加到开挖面上。

(3)将管片激活, 即将千斤顶推力作用到管片上。

(4)将盾尾注浆部分的土体钝化, 对注浆属性进行激活, 注浆压力施加其上。

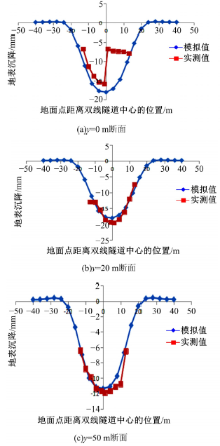
为验证C值在实际工程当中的有效性, 采用不同断面处地表横向沉降曲线图进行对比, 如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同断面处地表沉降对比Fig.6 Comparison of subsidence at different cross sections

通过图6可知:图6(a)的右侧部分的点实测值与模拟值相差较大, 除此之外, 绝大多数点的数值分析结果与实测数据基本一致。表明数值模拟的精度与实测值基本保持一致, 经过数值模拟之后的结果具有很大的可信度。图6(a)中的非正常波动可能是由于施工现场复杂的地质条件所导致(场地地层中存在部分淤泥土, 会受到盾构掘进相当大的干扰), 致使相应位置的地表沉降不均匀。图6(a)右侧部分点实测值表示的地表沉降是右线隧道掘进的结果, 通过分析, 推测出现这种结果的原因是:在施工现场, y=0断面的右线区域是各种施工机械出入场地的必经之域, 长时间的碾压, 致使监测点被损坏, 故实测结果不可靠。

隧道的轴心距可取为 L=1.17D=7、L=3.5D=21、L=8.17D=49,且令其余参数恒定。从简化建模角度出发, 将土层视为一层均质的粉质黏土。其具体参数的取值可参照表2中的粉质黏土2:内摩擦角 φ取为14.7° 。工作荷载:掘进压力为120 kPa、千斤顶推力为100 kN、注浆压力为150 kPa。两侧隧道同一时间开始掘进, 并采取一样的开挖速率, 据此创建双线盾构隧道施工阶段的分析模型。选y =30 m的断面, 绘制出地表在不同的轴心距作用下的沉降曲线, 如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
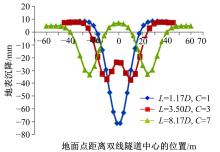	图7 y=30 m断面不同隧道轴心距引起的地表沉降曲线Fig.7 Horizontal subsidence curve caused by different tunnel axis distance at y=30 m cross section

通过图7可知:当逐步增大隧道轴心距使其余参数恒定时, 沉降曲线的形态随之发生变化。由于 C=L/i(i> 0),当采用的隧道轴心距比较小, 且与之相应的 C< 2时, 对应的地表沉降曲线形状是“ 单峰” ; 当扩大轴心距至相应的 C> 2时, 对应的地表沉降曲线形状从“ 单峰” 变成“ 双峰” ; 当继续扩大轴心距至相应的 C=7时, 对应的地表沉降曲线继续表现为“ 双峰” 形态。通过上述剖析, 即可对前文提出的地表沉降曲线变化规律进行验证。由图7可知, 隧道地表最大沉降量皆在“ 单峰” 或“ 双峰” 的峰值位置出现, 当轴心距不断增大时, 最大沉降量将随之减小。上述情况出现的原因是由于当单一更改隧道间距时, 实际上更改的仅是隧道左右两线地表沉降槽彼此之间影响区域的范围。当隧道轴心距取小值时, 两线彼此之间影响区域较大, 重叠后产生较大的沉降峰值; 当扩大轴心距至某一程度时, 叠加后的沉降量峰值小于“ 单峰” 峰值; 当继续扩大轴心距时, 最大沉降量主要由“ 单峰” 的峰值决定; 当继续扩大轴心距至“ 双峰” 分离、彼此互不干扰区域时, “ 单峰” 的峰值在理论上就是最大沉降量, 不会因轴心距的继续扩大而扩大。

4.2.1 土体弹性模量的影响

隧道土体的弹性模量E分别取为14、50、90、140 MPa, 且使其余参数恒定, 土体参数可参照表2中粉质黏土2:内摩擦角 φ取为14.7° 。绘制出地表在不同弹性模量下的沉降曲线, 如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 不同土体弹性模量下的最大地表沉降Fig.8 The maximum surface subsidence under different soil elastic modulus

通过图8可知:最大地表沉降在弹性模量取14 MPa时, 最大地表沉降达到83 mm; 而其在弹性模量为50 MPa时, 减至25 mm。由此表明, 土体的弹性模量在某一区间内, 对因盾构施工导致的地表沉降量的最大值有明显影响:在此区间内, 当弹性模量不断增大时, 地表沉降量的最大值随之明显减少, 但当其增大到一定程度时, 若继续增大, 沉降量的减少将逐步减缓。

4.2.2 土体黏聚力的影响

隧道土体的黏聚力c分别取25、35、45、55 kPa, 且使其余参数恒定, 土体参数可参照表2中粉质黏土2:内摩擦角 φ取为14.7° , 弹性模量取E=14 MPa。绘制出地表在不同黏聚力下的沉降曲线, 如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 不同土体黏聚力下的最大地表沉降Fig.9 The maximum surface subsidence under different soil cohesions

通过图9可知:当黏聚力不断增大时, 因盾构施工导致的最大地表沉降量随之减少, 且变化趋势较为平缓。

4.2.3 土体内摩擦角的影响

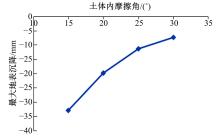
隧道土体的内摩擦角 φ分别取15° 、20° 、25° 、30° , 且使其余参数恒定, 土体参数参照表2中粉质黏土2:弹性模量取为E=14 MPa, 黏聚力取为c=45 kPa。绘制出地表在不同内摩擦角下的沉降曲线, 如图10所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 不同土体内摩擦角下的最大地表沉降Fig.10 The maximum surface subsidence under different soil friction angles

通过图10可知:当内摩擦角不断增大时, 因盾构施工导致的地表沉降量的最大值随之减少, 且土体的内摩擦角在取某一较小值区间内, 对地表沉降量的最大值有明显影响, 但随内摩擦角增大到某一程度时, 若继续增大, 则沉降量的减少将逐步减缓。

当盾构隧道采取异步法施工时, 先行、后行开挖断面间距 d可为 D、2D、5D(D为隧道直径), 且其余参数保持恒定。选y=0 m的断面, 当左线隧道施工到60 m时, 绘制出地表在不同的开挖距离下的沉降曲线, 如图11所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
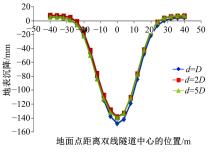	图11 不同开挖面距离下y=0断面地表沉降曲线Fig.11 Surface subsidence curve of y=0 section of different excavation distance

通过图11可知, 当 d=D时, 与之相应的最大沉降量为148.39 mm; 当 d=2D时, 与之相应的最大沉降量为138.91 mm; 当 d=5D时, 与之相应的最大沉降量为138.31 mm。通过上述情况可知, 左、右两线隧道彼此之间的影响在开挖面间距取小值时明显, 故而使二者叠加后导致的沉降值最大, 当开挖面间距 d> 2D时, 双线隧道的地表沉降因异步开挖施工造成的影响近乎不计。