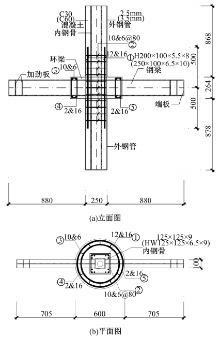
本文的节点模型主要包括外约束方钢管、柱内钢骨、钢梁、柱内混凝土、环梁混凝土及钢筋骨架几个部分, 模型试件的具体构造如图1所示。钢梁的上、下翼缘伸入节点核心区与柱内钢骨采用全对焊形式连接, 在钢骨翼缘节点区之外均匀布置一定数量的抗剪栓钉以确保柱内钢骨与混凝土之间的协同工作, 本文的有限元计算模型采用真实试件1/2比例建模。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 节点试件构造图Fig.1 Structural diagram of specimen

本文研究外钢管径厚比、节点区(钢梁)高度、内钢骨形式(采用方钢管和H型钢两种形式)、混凝土强度、轴压力5个参数对节点滞回性能的影响, 共建立了6个分析模型, 其各试件参数如表1所示。

表1

Table 1

表1(Table 1)

表1 试件参数表 Table 1 Component parameter table 试件编号 钢梁规格 钢管厚度(mm)/径厚比 钢骨规格 混凝土等级 轴压比/轴压力(kN) 柱轴压承载力/kN N1 HN200× 100× 5.5× 8 2.5/100 125× 125× 9 C30 0.41/1000 2458.3 N2 HN200× 100× 5.5× 8 2.5/100 125× 125× 9 C30 0.82/2000 2458.3 N3 HN200× 100× 5.5× 8 2.5/100 125× 125× 9 C60 0.60/2000 3311.1 N4 HN200× 100× 5.5× 8 2.5/100 HW125× 125× 6.5× 9 C30 0.45/1000 2228.1 N5 HN200× 100× 5.5× 8 3.5/71 HW125× 125× 6.5× 9 C30 0.43/1000 2333.8 N6 250× 100× 7× 10 2.5/100 HW125× 125× 6.5× 9 C30 0.45/1000 2228.1 注:柱轴压承载力计算方法参考文献[10]相关内容求得; 除N1~N3试件的钢骨、N6试件的钢梁采用非标准型钢外, 其余试件的钢梁及H型钢钢骨均采用《热轧H型钢和部分T型钢》(GB/T11263— 2010)中的标准窄翼缘型钢及宽翼缘型钢。

表1 试件参数表 Table 1 Component parameter table

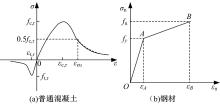
本文模型采用C30、C60两种混凝土, 混凝土的本构模型采用ABAQUS软件中提供的塑性损伤模型, 该模型能够较好地模拟混凝土在往复荷载作用下的刚度退化等特性。对于钢管约束区域的混凝土, 其受拉、受压本构关系采用文献[11]中的本构模型, 如图2所示。对于普通混凝土, 其受拉、受压本构关系采用文献[12]附录C提供的曲线, 如图3所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 约束混凝土本构关系Fig.2 Constitutive relation of confined concrete

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 普通混凝土及钢材本构关系Fig.3 Constitutive relation of ordinary concrete and steel

本文模型中钢管、钢骨、钢梁采用Q235钢材, 钢筋采用HPB300、HRB400两种类型, 强化准则采用了ABAQUS软件中能够反映包兴格效应的混合准则。钢材、钢筋的本构关系采用两折线本构关系, 如图3所示, 弹性模量取2.06× 1 05MPa, 泊松比取0.3, 屈服强度及极限强度取现行规范值^{[12, 13]}。

本模型采用二次三维实体单元, 钢结构及混凝土采8节点减缩积分格式的C3D8R三维实体单元, 而钢筋采用三维桁架T3D2单元。单元网格划分的尺寸在经过试算并考虑求解速度和精度的基础上确定, 节点模型主要部件(以N1为例)网格划分如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 模型主要部件网格划分Fig.4 Meshing of main components of a model

本文模型中钢管与混凝土的接触采用ABAQUS中的面面接触, 在法线方向钢管与混凝土不能相互穿透, 因此采用“ 硬接触” 来模拟, 在切线方向钢管与混凝土服从库伦摩擦准则, 根据文献[14]的研究成果, 摩擦因数取0.6; 为模拟钢骨抗剪栓钉所起到的协同工作作用, 钢骨采用嵌入命令进行定义, 不考虑与混凝土之间的相对滑移, 钢筋骨架均同样采用嵌入命令定义, 不考虑其与混凝土之间的相对滑移。

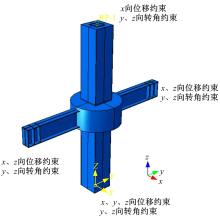
为了完全模拟边界条件, 在柱底部10 cm范围内, 将其材性的强度和刚度定义为无穷大(取弹性模量E=1 010MPa, 屈服强度f_y=1 010MPa), 在其底面的中间分界线上施加约束, 限制其x、y、z向位移约束, y、z向转角约束以模拟铰的转动; 在两侧梁端150 mm范围内上下翼缘施加约束, 限制其x、z向位移约束, y、z向转角约束以模拟梁端连杆支承; 在柱顶上20 mm处建立一参考点, 将柱顶界面与该参考点建立耦合, 并对该参考点施加约束, 限制其x向位移, y、z向转角约束, 如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 边界条件示意图Fig.5 Boundary condition schematic diagram

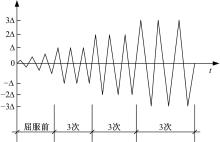
节点的拟静力试验加载方式一般分为梁端加载荷和柱端加载, 由于柱端加载能够较为真实地模拟地震来临时所产生的重力二阶效应, 因此本文采用文献[15]中考虑重力二阶效应的柱端加载方式进行加载, 首先在柱顶施加一恒定轴向力(按参数表取值), 接着在柱顶施加水平往复荷载, 采用位移控制的循环加载模式, 试件屈服前以屈服位移的1/4、1/2、3/4为每级荷载各循环1次, 屈服后以屈服位移的整数倍为每级荷各循环3次, 经有限元单调加载试算, 以荷载降至峰值荷载的0.85倍左右为破坏标志^[15], 分别制定各试件的循环加载制度, 其加载制度及加载示意图如图6、图7所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 循环加载制度Fig.6 Cyclic loading system

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 循环加载示意图Fig.7 Cyclic loading schematic diagram

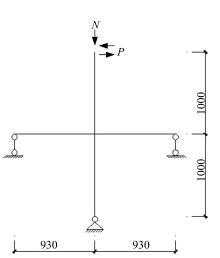
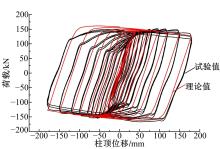
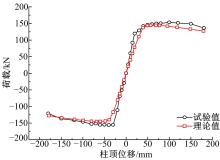
本文一共进行了两类共8个全尺寸圆钢管约束H型钢混凝土柱-钢梁(RC梁)节点的拟静力试验研究, 其中试件SH-2为圆环梁形式的圆钢管约束H型钢混凝土-柱钢梁节点, 试件高4.375 m, 试件宽3.370 m, 如图8所示, 结构形式为400 mm圆钢管约束H型钢混凝土柱, 采用钢筋混凝土圆环梁对节点区进行补强, 柱内型钢采用HW175× 175× 7.5× 11宽翼缘标准H型钢; 钢梁采用HN300× 150× 6.5× 9窄翼缘标准H型钢。其形式与本文中设计的试件结构形式类似, 因此选取SH-2试件, 采用上述建模及参数设置方法对其进行非线性有限元模拟分析, 图9、图10为有限元数值模拟计算得到的柱顶位移滞回曲线、骨架曲线与试验得到的曲线对比。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 试件拟静力试验加载Fig.8 Pseudo static test loading of test parts

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 滞回曲线对比Fig.9 Comparison of hysteresis curve

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 骨架曲线对比Fig.10 Comparison of skeleton curve

由数值模拟曲线和试验曲线的对比可以看出, 无论时滞回曲线还是骨架曲线, 理论和试验均吻合较好, 但由于理论分析相对于试验要理想一些, 故理论分析所得到的曲线相对对称、规整, 并与试验结果之间存在一定的偏差, 但总体相差不大。由此可以验证以上建模方法及参数选取的合理性, 故其数值模拟结果具有参考价值。

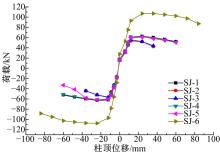
图11给出了6个节点试件的柱顶荷载-位移(P-Δ )滞回曲线。经分析可以看出:由于每个试件柱顶水平屈服位移和破坏位移不同, 因此根据文献[15]制定的循环加载制度也不同; 随着轴向压力的增加, N2、N3试件的破坏位移较其余试件小, 适当地增加节点区高度(钢梁高度)可以增大试件的抗震承载力, 如N6试件所示, 外钢管径厚比、钢骨形式、混凝土强度等参数对试件滞回性能的影响不大; 从6个试件的柱顶荷载-位移滞回曲线来看, 各试件的滞回曲线形状较为类似, 在循环加载的初期, 滞回曲线呈平行四边形, 随着循环加载的持续, 滞回曲线逐步由平行四边形转变为矩形, 这种形态的滞回曲线既不同于典型的钢结构节点滞回曲线形态(梭形或纺锤型), 也不同于典型的混凝土结构节点滞回曲线形态(枣核型), 且进入加载后期时, 6个试件的滞回曲线均呈现出一定的“ 反刚度” 现象, 即试件的每一位移幅值循环的荷载峰值出现在由位移最大位置返回位移零位的过程中, 这表明此类钢混组合结构新型节点有其自身的特征, 各节点滞回曲线的丰满程度均大大超过了相应钢框架节点及混凝土框架节点滞回曲线的丰满程度, 表现出了非常良好的抗震耗能性能。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 各试件柱顶P-Δ 滞回曲线Fig.11 P-Δ hysteretic curve of component

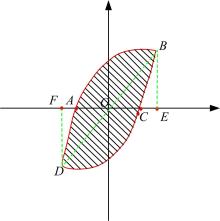
目前, 结构物在地震作用下耗能性能的评价指标一般为能量耗散系数E和等效粘滞阻尼系数h_e两种, 两个指标都是以荷载-位移滞回曲线所包围的面积来衡量。能量耗散系数E的计算由文献[15]给出, 等效粘滞阻尼系数h_e的计算由文献[16]给出, 其计算图示如图12所示。

E=S(ABC+CDA)S(OBE+ODF)(1)he=12π·S(ABC+CDA)S(OBE+ODF)(2)

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 耗能性能计算图示Fig.12 Calculation diagram of energy dissipation performance

表2为试件耗能性能指标。由表2可知:6个试件的能量耗散系数E在3.04~3.96区间, 等效粘滞阻尼系数h_e在0.48~0.63区间, 根据相关研究结果表明, 钢筋混凝土节点的等效粘滞阻尼系数h_e为0.1左右, 型钢混凝土节点的等效粘滞阻尼系数h_e为0.3左右, 本文的6个新型节点试件的h_e均大于型钢混凝土节点的等效粘滞阻尼系数, 说明该类节点的耗能性能良好, 满足结构抗震设计要求。

表2

Table 2

表2(Table 2)

表2 试件耗能性能指标 Table 2 Energy dissipation performance of components 试件编号 E he N1 3.96 0.63 N2 3.69 0.59 N3 3.92 0.62 N4 3.21 0.51 N5 3.39 0.54 N6 3.04 0.48

表2 试件耗能性能指标 Table 2 Energy dissipation performance of components

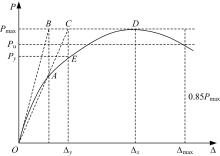
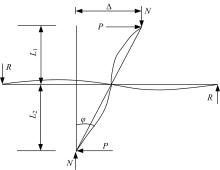
根据2.1节得到的各试件滞回曲线, 按照文献[15]的方法取上面6个试件的荷载-位移滞回曲线各加载等级第一循环正向峰值点的包络线即得到骨架曲线, 图13给出了6个试件的柱顶荷载-位移骨架曲线, 可以看出6个试件的骨架曲线形式较为类似, 均经历了弹性、屈服、极限、破坏4个阶段。根据文献[15]中对构件屈服、极限、破坏荷载及位移的相关规定, 采用“ 通用屈服弯矩法” ^[16](见图14)可求得各阶段的荷载、相对应的位移及层间变形角(P_y、Δ _y、P_max、Δ _u、P_u、Δ _max), 根据节点破坏时的位移Δ _max和节点屈服时的位移Δ _y, 可求得节点试件的位移延性系数u=Δ _max/Δ _y, 还可根据几何关系(见图15)求得各阶段的层间变形角φ _y、φ _u、φ _max, 根据节点破坏时的层间变形角φ _max和节点屈服时的层间变形角φ _y, 可求得节点试件的变形角延性系数u_φ =φ _max/φ _y, 各个试件的延性指标如表3所示。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 各试件柱顶P-Δ 骨架曲线Fig.13 P-Δ skeleton curve

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 通用屈服弯矩法示意图Fig.14 Schematic diagram of general yield bending moment method

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 几何关系Fig.15 Geometric relation

表3

Table 3

表3(Table 3)

表3 各试件屈服、极限、破坏及延性指标 Table 3 Yield, limit, failure and ductility of specimen 试件 编号 屈服 极限 破坏 u uφ Py /kN Δ y /mm φ y /rad Pmax /kN Δ u /mm φ u /rad Pu /kN Δ max /mm φ max /rad N1 60.05 13.10 0.0065 62.51 23.89 0.012 53.13 58.78 0.027 4.49 4.08 N2 49.89 11.25 0.0056 55.35 13.28 0.0066 47.05 28.53 0.014 2.54 2.55 N3 50.08 10.09 0.0051 55.10 12.03 0.0060 46.84 29.49 0.015 2.92 2.89 N4 56.71 12.51 0.0062 61.49 23.38 0.012 52.27 53.21 0.027 4.25 4.29 N5 58.89 13.25 0.0066 62.11 25.01 0.013 52.79 54.83 0.027 4.14 4.15 N6 94.05 14.10 0.0070 107.67 23.85 0.012 91.52 82.15 0.041 5.83 5.86

表3 各试件屈服、极限、破坏及延性指标 Table 3 Yield, limit, failure and ductility of specimen

由表3可知:6个节点试件的位移延性系数在2.54~5.83区间, 变形角延性系数在2.55~5.86区间, 均满足钢筋混凝土结构对延性系数不小于2的要求, 但随着轴压比的增大试件的延性系数大大降低; 6个节点试件的弹性极限层间位移角φ _y在0.0051~0.0070区间, 弹塑性极限层间位移角φ _max在0.014~0.041区间, 根据文献[17]中的规定, 多遇地震作用下, 多、高层钢结构的弹性层间位移角限值[θ _e]为1/250=0.004; 罕遇地震作用下, 多、高层钢结构的弹塑性层间位移角限值[θ _p]为1/50=0.02, 本文中6个节点试件的弹性极限层间位移角均大于规范限值, 除N2、N3(高轴压比作用下)外, 其余4个试件的弹塑性极限层间位移角也大于规范限值, 这进一步表明即使在更为严重的地震作用下, 试件依然能够保持优越的延性性能, 但同样轴压比的增大会降低试件的弹塑性极限层间位移角, 降低其延性性能。

进一步考察不同参数对试件各状态及延性指标的影响可以发现:外钢管径厚比、混凝土强度及内钢骨形式对该类型节点延性性能影响不大, 但随着轴向压力的增大, 其屈服、极限、破坏荷载及各延性指标均明显下降, 如试件N2、N3所示, 同时, 在构件满足“ 强柱、弱梁、节点更强” 的基础上, 适当增大节点区(钢梁)高度, 有助于提升节点试件在地震作用下的延性性能, 如试件N6所示。

为了考察该节点核心区各部分在加载过程中的应力分布及变化情况, 图16分别给出了N1、N4、N5、N6试件在柱顶往复荷载作用下正向6、12、36 mm第一循环、60 mm第三循环时的节点核心区应力云图以及N2、N3试件在柱顶往复荷载作用下正向6、12、24 mm第一循环、36 mm第三循环时的节点核心区应力云图。由图16可以看出, 当柱顶位移为6 mm时, 6个试件钢梁与环梁交界处钢梁翼缘应力最大, 这预示了此类节点最终出现塑性铰及破坏的地方位于钢梁与环梁交界处, 为梁端破坏, 位移继续加大至12 mm时, 梁端翼缘应力继续增大并扩展至腹板, 同时柱内钢骨腹板、环梁箍筋、柱箍筋上的应力也不断增加, 随着位移的继续增大, 最终破坏时梁端翼缘与腹板的应力超出Q235钢材的屈服应力, 而未达到其极限应力, 说明此类节点最终破坏形态为梁端的局部曲屈破坏而非强度破坏, 破坏时N1、N2、N3试件柱内钢骨腹板、环梁箍筋、柱箍筋均未达到其屈服应力, N4、N5、N6试件柱内钢骨腹板、环梁箍筋、柱箍筋局部达到超过其屈服应力, 但由于约束混凝土的存在, 并未发生曲屈破坏。因此, 从6个试件的应力随位移加载的变化趋势、试件的破坏顺序及最终的破坏形态来看, 此类新型节点均符合“ 强柱、弱梁、节点更强” 的抗震设计要求, 混凝土环梁的存在使得塑性铰外移有效地保护了节点核心区。

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 各试件节点核心区应力随位移加载变化分布Fig.16 Variation distribution of stress with displacement in core area of each specimen

进一步考察不同参数对试件应力分布的影响可以发现:外钢管径厚比、混凝土强度、节点区(高度)对其应力分布及最终破坏形态没有太大的影响, 但随着轴压比的增大, N2、N3试件梁端翼缘达到屈服状态的时间会提前, 相应地这两个试件破坏也会提前, 破坏时的柱顶位移为36 mm左右, 仅仅是其余试件破坏时柱顶位移的60%, 这是由于增大轴向压力会大大增大试件的重力二阶效应所致, 钢骨形式的不同对其应力分布也有影响, N1、N2、N3试件的钢骨形式为方钢管, 其钢骨腹板厚度为N4、N5、N6(腹板形式为H型钢)试件的两倍, 其抗剪能力强于H型钢钢骨, 因此, 对于柱内钢骨形式为H型钢的试件, 若其抗剪承载力不足时, 可参考文献[13]的相关内容对其进行补强。