作者简介:徐亮(1980-),男,副教授,博士.研究方向:复杂热端部件的冷却技术.E-mail:xuliang@mail.xjtu.edu.cn
基于已有文献中的实验数据,提出了一种采用 RNG-k-ε湍流模型能较准确地模拟旋转冲击射流靶面传热特性的数值计算方法。采用该方法,针对内置螺旋杆、内置扭转带和内置导叶片三种类型的激发旋流方式,得出了来流 Re数对喷嘴出口射流旋度的影响,并分析了旋度对靶面换热特性的影响。数值结果表明:不考虑 Re数影响的旋度评估方式会出现很大偏差,螺旋角30°和45°下喷嘴出口气流的旋度对来流 Re数比较敏感。三种不同喷嘴的旋流在冲击靶面会产生不同的高换热“冷斑”,“冷斑”的形状及面积大小与喷嘴出口旋度有关。气流旋度越大,换热 Nu峰值越小,但换热均匀性提高。不同结构喷嘴下靶面换热特性取决于来流 Re数和旋度的综合效应。本研究中,相同条件下内置螺旋杆产生的旋流冲击射流在靶面具有最佳的均匀高效换热性能。
Based on the experimental data of swirling impinging jet from published literature, a numerical simulation method with RNG-k-ε turbulence model was developed to accurately simulate heat transfer characteristics of swirling impinging jets. Three types of inserts, screw rod, twisted tape and guide vane, were used to produce the swirl flow. Swirling impinging jets issuing from the nozzles of these inserts were numerically studied. The effect of jet Reynolds number on swirling number at the exit of the nozzles was evaluated and the effect of swirl number on heat transfer of the swirling impinging jets was analyzed. Numerical results show that the large deviation of swirl number occurs as jet Reynolds number is not considered. The swirl number of the swirling jets by the inserts with medium helix angles of 30° and 45° is very sensitive to changes in jet Reynolds number. Different patterns of red spot with high heat transfer rates are shown on the target surface by swirling impinging jet issuing from the nozzles. Shapes and sizes of red spots are related to swirl number of the swirl jets. The peak of Nussle number is increased and the uniformity of heat transfer is enhanced as the swirl number increases. Heat transfer characteristics of the swirling jets depend on the combined effect of jet Reynolds number and swirl number of the jets. The optimum swirl generator is the type of insert with screw rod. Comparing to the other two swirl generators of the inserts with twisted tape and guide vane, the highest heat transfer coefficient with the best uniformity on the target surface by this swirl generator can be achieved under the same working condition.
旋转冲击射流作为一种特殊的冲击射流, 既有传统光滑圆孔冲击射流的高换热率, 又有较好的换热均匀性, 在工业中有较好的应用前景。旋转冲击射流一般可由特殊几何结构的喷嘴产生旋流, 相比于传统冲击射流, 旋转冲击射流是轴向速度和切向速度掺混的气流在射流空间内交互作用[1], 射流空间的流场异常复杂。旋转射流不仅具有传统圆孔冲击射流的轴向速度、径向速度引起的滞止、卷吸及流线弯曲等复杂特征, 还增加了出流大尺度旋涡的流动演化、掺混破裂等更为复杂的涡流结构。在旋流射流的研究中一般采用旋流数S(或者旋度)来表征喷嘴出流的旋流强度。Toh等[2]对不同定义旋流数的差异性进行了评估, 强化了研究旋流问题时对旋流数这一参数的认识。这也说明表征旋流强度的方法没有统一, 旋转冲击射流问题还有待进一步的深入研究。
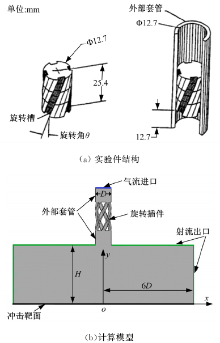
目前, 产生旋转射流的喷嘴主要有内置螺旋杆、内置导叶片和内置扭转带三大类, 就旋转冲击射流的流动及传热实验研究来看, 在内置螺旋杆方面, Huang 等[3] 通过内置一个外表面开有四条螺旋凹槽的插件形成旋转射流。试验了4种角度(θ =0° , 15° , 30° , 45° )下的流动及换热情况。发现旋转射流不仅改善了径向传热的均匀性, 同时也比普通射流具有更高的平均努塞尔数。Bakirci 等[4]研究了与 Huang 等尺度的圆管, 区别在于圆管内螺旋杆更长, 且螺旋插件截面成类扇形, 试验了4种角度(θ =0° , 22.5° , 41° , 50° )。得出径向均匀性传热最佳的结构螺旋角为 50° , 喷管距靶面高度h/d=14。在置入导叶轮方面, 杨会群等[5]研究了一种环形旋转射流的传热特性, 研究表明在中小冲击距离下, 局部压力和传热系数在冲击靶板上的分布与传统环形冲击射流相比更不均匀, 但总体传热性能更好。Brown等[6]用热膜成像技术比较研究了两种不同导叶产生的旋转射流流动及传热特性, 并研究了旋转射流时靶面热流量的脉动效应。在置入扭转带方面, Ianiro等[7]研究了一个十字交叉型扭转带的圆管旋转冲击射流。在整个实验中, 只有在y/W=6下, 旋转冲击射流的平均Nu数才高于圆孔射流下的Nu数。Nuntadusit等[8]研究了插入扭转带的单个圆管旋转喷射和圆管群的阵列旋转喷射。对于单个圆管旋转喷射, 旋转数为 0.4, 扭转带宽度与节距之比y/W=3.4 的换热性能最佳。陈玉阳等[9]研究了单根圆管内插入一个扭转带的旋转射流。圆管内径为 3 mm, 扭转条与圆管等径, 节距为 15 mm, 结果表明低雷诺数下径向换热均匀化效果明显。
上述文献基本都是围绕单一类型喷嘴开展旋转冲击射流的传热特性研究, 同时一般选择与传统单个圆孔冲击射流或同尺寸多个直槽道喷嘴来进行传热性能的差异性分析。虽然Eiamsa-ard 等[10]也对比了几种不同类型结构的旋转射流喷嘴, 但只是基于同Re数下进行的简单比较分析。由于产生选择射流的喷嘴几何结构的不同, 激发的旋流特征存在着很大差异, 这样也势必影响靶面的传热性能。同时研究者所采用的不同试验工况和不同定义的旋度, 这样在实际应用中很难去甄别与借鉴已有的研究成果。本课题组之前对一种类螺纹孔结构的旋流射流进行了数值仿真研究[11, 12], 本文在前期探索和积累的有关旋流射流数值模拟计算方法基础上, 选择了一个常见的旋度评估计算方法, 分析了喷射气流Re数与这一旋度之间的关系, 并在同一旋度下分析了不同结构喷嘴旋转冲击射流传热特性的差异。
根据Huang等[3]的实验对象, 建立相应的计算模型, 如图1所示。
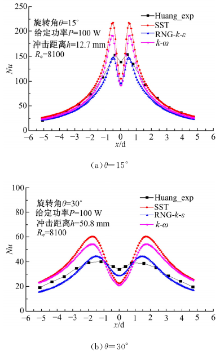
图2给出不同湍流模型下局部Nu数计算值, 从图中可以看出, 三种湍流模型计算值分布趋势与实验结果基本一致, 在中心滞止点区三种湍流模型计算较为一致, 与实验数值偏差较大。推测原因是滞止点区域气流流动缓慢, 在靶面附近为层流流动, 采用湍流模型去模拟层流, 势必都会出现较大的预测偏差。在峰值点预测方面, RNG-k-ε 湍流模型的计算结果和实验值吻合最好, 而k-ω 、SST湍流模型在两个峰值处均比实验值要大, 且峰值位置朝径向外移。另外, RNG-k-ε 采用壁面函数拟合近壁面流动, 在划分网格时, 不需要在壁面区加密, 只需要把第一个内节点配置到湍流充分发展的区域[13], 同等计算精度下RNG-k-ε 比其他两种模型所需的网格数要少, 在h=2d时, 整个流体域网格总数约为220万。本文采用的网格都进行了大量的试算, 以靶面Nu数变化在2%以内, 视为计算网格具有网格无关性, 综合考虑, RNG-k-ε 湍流模型对旋转冲击射流的传热计算有较好的精度和较高的效率, 本文接下来的研究都将采用这一湍流模型。
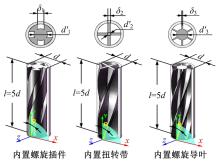
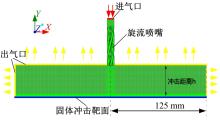
由于激发旋流喷嘴结构常见的三种为内置螺旋杆(以下简称NCJ喷嘴)、十字扭转带(以下简称NZD喷嘴)、内置导叶片(以下简称DYE喷嘴)。为了在几何尺寸上基本一致, 三种旋流喷嘴都是取圆管内径d=9 mm。考虑到集气室的整流效应, 在不同激发旋流喷嘴段上游设置了一段光滑圆孔(内径为9 mm)整流段, 高度为d。激发旋流的喷嘴结构段高度l=5d , 以15° 螺旋角为例, 各喷嘴几何模型如图3所示, δ 1=2.5 mm , δ 2=1 mm, δ 3=0.5 mm, d'1=5 mm, d'2=0.7 mm, d'3=4.5 mm。根据这三种不同旋流方式的激发旋流喷嘴结构, 以通流区域作为该段喷嘴流场的计算域建立喷嘴旋流部分的计算模型。采用ICEM-CFD对各模型进行网格划分, 鉴于激发旋流喷嘴的通流结构复杂性, 所有激发旋流喷嘴段通流部分采用四面体的非结构化网格, 而喷嘴的光滑圆孔整流段、射流空间与金属靶面实体均采用六面体的结构化网格。
考虑到在实际应用中, 设备的换热区域多为一定厚度的金属, 本研究选取的射流靶面为厚度1 mm的不锈钢板。冲击距离h/d=4的射流空间, 最大网格不超过1 mm, 所有近壁面均加密, 近壁面第一层网格为0.15 mm, 网格增长率为1.2。同时在滞止点冲击附近区域, 网格进行了适度的加密处理。金属固体域与流体域采用流固耦合交界面, 两种交界处的网格点一一对应, 以保证热流通量传输的守恒。使用商业软件ANSYS FLUENT进行计算, 计算时采用流固气热耦合计算方法, 对靶面求解固体域内的温度场, 对射流空间及喷嘴通流部分求解流场。
边界条件的设置如下:喷管进口设置质量流量, 当量直径取9 mm, 基于研究的来流Re数给定进口流量, 即m=Reπ dμ /4(其中
冲击射流的靶面换热Nu数为:
式中:
关于旋转射流的旋流数(旋度)的定义, Drake和Hubard(1963)最早给出了它的定义:①切向动量通量和轴向动量通量之比; ②中心锥角的正切值。
第一种定义的公式为[14]:
式中:
式中:r1、r2分别为旋流喷嘴中置入件的内径和外径。该公式旋度值只取决于旋流激发的喷嘴结构。针对公式(2), 有文献提出了一种计算更为方便的替代性公式[14], 即:
式中:
选取5种不同的来流Re数, 即Re=5000, 6000, 8000, 10000, 12000来依次计算不同来流Re数下三种喷嘴不同螺旋角度(15° , 30° , 45° , 60° )下激发旋流的旋度, 采用公式(3)和(4)计算的旋度值绘制在图5中。公式(3)只与喷嘴结构有关, 对于内置件尺寸固定的喷嘴来说, 其值为螺旋角的单值函数。角度不变时, S值为一个定值。而公式(4)不仅考虑结构的影响, 还与来流的Re数有关。图中可以看出, 当螺旋角
可以看出, 不考虑Re数的公式(3)很难去评估不同运行速度下的旋转射流。三种喷嘴在不同角度下, S值一般会随着Re数的增大而缓慢地增大。但由于结构不同导致的旋流复杂性, 也会出现不同的变化。如
由以上分析可知, 进口Re数显然会对旋流射流的旋度产生影响, 因此, 本文后续研究将采用旋度的第二种定义, 即公式(4)进一步分析旋度对旋流射流换热特性的影响。
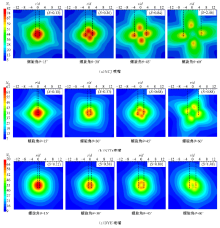
图6为Re=10 000时三种旋流喷嘴在不同旋度下的靶面Nu数分布。从图中可以看出, 对于同一类型旋流喷嘴, 随着螺旋角的增大, 旋度也随之增大, 靶面上的“ 冷斑” (Nu峰值区域)逐渐变淡且越来越分散, 但相对较高换热的分布区域(绿色区域)面积越来越大, 且形成的形状也随之发生变化。这说明, 对于同一类型的旋流喷嘴, 随着旋度的增大, 滞止点附近的当地Nu峰值会有所降低, 旋流在靶面的扩散区域也随之发生变化, 但扩散面积越来越大, 即换热均匀性越来越好。这可能是因为喷射气流的旋度越大, 对周围气流的卷吸效应更大, 喷射中心的轴向速度衰减更快, 而扩散的传播区域更大。同时可以看出, 随着旋度的增大, Nu峰值径向外移的距离(图中用黑虚线表示)更为明显。这种外移量, 不同类型的喷嘴表现出较为明显的差异, NCJ喷嘴的偏移量最大, 其次是NZD喷嘴, DYE喷嘴最小, 这表明采用内置导叶(DYE)的旋流喷嘴, 冷却气流冲击到靶面以后相对比较集中, 而采用内置螺旋杆(NCJ)的喷嘴, 气流的扩散性最强。
从上节分析可知, 喷嘴内置件
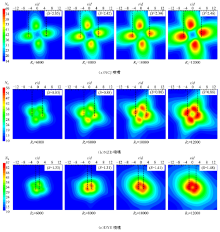 | 图7 三种旋流喷嘴在不同Re下的靶面Nu数分布Fig.7 Local Nusselt number on target surfaces for three nozzles at different Reynolds numbers |
由图5可知, 在
 | 图8 S≈ 0.37不同类型喷嘴下靶面当地Nu数和平均Nu数Fig.10 Local and average Nusselt number on target surfaces for three nozzle with S≈ 0.37 |
靶面平均努塞尔数为:
从图8(a)可知, 在同一Re数下相近旋度条件下, NCJ喷嘴的靶面局部Nu数最高, 即NCJ喷嘴冲击射流的靶面换热效果最好, 三种不同旋流喷嘴的靶面Nu数峰值均在滞止中心点的外围, 其中NZD喷嘴与DYE喷嘴的Nu数峰值大约出现在径向的
(1)不考虑Re数影响的旋度评估方式会出现很大偏差。三种喷嘴在不同螺旋角度下, S值一般会随着Re数的增大而缓慢地增大, 尤其在中等螺旋角度时, 旋度对Re数的变化比较敏感。
(2)同一类型的喷嘴, 随着旋度的增大, 靶面的Nu峰值越来越小, 但Nu峰值的径向位置距离滞止点越来越远, 同时较高换热区域面积越来越大, 即换热的均匀性越来越好。
(3)相近旋度下, 同一类型的喷嘴随着Re数的增大, 靶面的换热性能越来越好, 但靶面的Nu峰值的径向位置将保持不变; 同时高换热区域面积会进一步扩大, 但外围形状保持不变。
(4)不同类型的喷嘴, 旋流冲击射流靶面的换热性能取决于旋度和Re数的综合作用。相近旋度下就靶面的换热性能来说, 本研究中含有四个螺旋槽的内置螺旋杆为最佳激发旋流方式, 旋流冲击的靶面具有均匀高效的换热性能。其平均Nu数比内置十字扭转带的高出20%~40%, 比内置导叶的高出13%~35%。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|