鼠笼支撑一体化结构对薄壁球轴承承载性能的影响

引用本文

毛宇泽, 王黎钦. 鼠笼支撑一体化结构对薄壁球轴承承载性能的影响[J].吉林大学学报（工学版）, 2018,48(5): 1508-1514
MAO Yu-ze, WANG Li-qin. Influence of squirrel-cage flexible support on the dynamic performance of ball bearing[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1508-1514 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170652
Permissions

鼠笼支撑一体化结构对薄壁球轴承承载性能的影响

毛宇泽, 王黎钦

哈尔滨工业大学机电工程学院,哈尔滨 150001

通信作者:王黎钦(1964-),男,教授,博士生导师.研究方向:摩擦学.E-mail:lqwanghit@163.com

作者简介:毛宇泽(1988-),男,博士研究生.研究方向:滚动轴承动力学.E-mail:maoyuze163.com

基金:国家自然科学基金联合重点基金项目(U1637206);“973” 国家重点研究发展计划项目(2013CB632305)

摘要

建立了鼠笼柔性支撑一体化轴承的FEM-拟动力学迭代分析模型,采用FEM模型计算支撑结构和轴承滚道的变形,采用非圆滚道的拟动力学模型分析轴承动态特性。研究了一个鼠笼支撑一体化球轴承在载荷作用下的内部载荷分布,分析了柔性支撑一体化结构对球轴承动态特性的影响。结果表明,鼠笼支撑一体化结构使轴承内部最大接触载荷减小了10.94%,疲劳寿命增加了11.3%,轴承刚度大幅降低,打滑率上升了15.8%。并且,轴承套圈壁厚越厚,结果越接近刚性支撑假设的计算结果;轴承套圈壁厚越薄,鼠笼支撑带来的影响越显著。

关键词: 机械设计及理论; 滚动轴承; 鼠笼支撑; 结构变形; 载荷分布; 疲劳寿命

中图分类号:TH133.33 文献标志码:A 文章编号:1671-5497(2018)05-1508-07

Influence of squirrel-cage flexible support on the dynamic performance of ball bearing

MAO Yu-ze, WANG Li-qin

School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China

Abstract

An integrated squirrel-cage flexible support ball bearing quasi-dynamic iterative Finite Element Model (FEM) is established, which is used to calculate the deformation of the support structure and raceway. The dynamic characteristics of the bearing are analyzed using the noncircular raceway quasi-dynamic model. The internal load distribution of the integrated squirrel-cage flexible ball bearing is studied, and the influence of the integrated flexible support structure on the dynamic characteristics of the bearing is analyzed. The results show that the integrated squirrel-cage flexible support structure reduces the maximum bearing internal contact load by 10.94%, increases the fatigue lifetime by 11.3%, reduces the bearing radial stiffness by an order of magnitude, and increases the slide ratio by 15.8%.

Keyword: machine design and theory; rolling bearing; flexible support; structural deformation; load distribution; fatigue life

文章图片

0 引言

高端滚动轴承技术是一个国家的战略基础产业和核心技术之一。薄壁轻量化、部件集成化是滚动轴承技术的主要发展方向。鼠笼支撑一体化轴承正在逐渐成为航空航天轴承领域的技术趋势^{[1, 2]}。在这一结构中, 空心轴、轴承套圈、鼠笼支撑结构均为薄壁构件, 在外加载荷的作用下鼠笼支撑结构及薄壁空心轴会发生明显的结构变形, 导致薄壁轴承套圈随之变形, 对轴承动态性能产生的影响不可忽视。

传统的轴承分析方法是基于刚性结构假设^{[3, 4]}, 仅考虑接触弹性的Hertz接触理论模型^{[5, 6, 7]}。由于没有考虑薄壁套圈及柔性支承结构的结构变形, 这一理论不能完全适应滚动轴承的发展需求。文献[8, 9]在此基础之上提出谐波齿轮轴承和行星机构轴承的分析方法, 考虑了轴承套圈柔性。但是, 以上模型是针对行星齿轮轴承和谐波齿轮轴承, 而对于航空领域所用的鼠笼一体化轴承等异形轴承的研究则需要结合具体轴承的几何结构来完成。因此, 对于高转速下的鼠笼支撑一体化轴承进行系统的动态性能分析是航空发动机轴承未来发展中必不可少的关键性研究之一。Yao等^[10]将支撑形式简化为若干个固定位置的点支撑, 以此采用弹性理论计算薄壁轴承套圈的结构变形, 分析了薄壁球轴承的载荷分布。学者们^{[11, 12, 13, 14, 15]}建立了考虑套圈变形的轴承有限元分析模型, 但是用弹簧代替滚动体的方法无法准确求解轴承内部载荷, 且有限元模型无法考虑轴承内部接触微区特性及润滑状态, 难以准确分析轴承动态性能。

本文建立了鼠笼支撑一体化球轴承的拟动力学-FEM分析模型, 采用有限元模型计算鼠笼支撑一体化轴承套圈及鼠笼结构的变形, 采用非圆滚道的拟动力学模型计算轴承动态特性, 能够综合考虑轴承内部接触微区特性、润滑状态、鼠笼支撑结构变形的影响, 准确地预测鼠笼支撑一体化轴承的动态性能, 得到轴承支撑刚度、疲劳寿命及滚动体打滑率等分析结果, 为整机设计提供依据。

1 鼠笼支撑一体化球轴承的拟动力学-FEM迭代模型

1.1 非圆滚道球轴承的拟动力学修正模型

采用拟动力学方法建立非圆滚道的球轴承拟动力学模型, 用于进行套圈变形后的轴承动态性能分析。

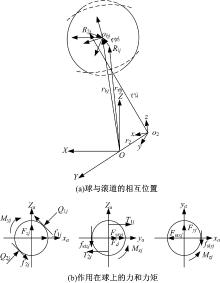
每个滚动体的受力状态如图1所示。第j号滚动体受到内外套圈通过油膜传递的沿法向的接触力Q_1j、Q_2j和沿切向的拖动力T_1j、T_2j,保持架的法向作用力F_srxj、F_sryj和切向力f_srxj、f_sryj,油气混合物的阻力F_dj和滚动体自身的惯性力F_j和惯性力矩M_j。

	Figure Option View Download New Window
	图1 滚动体受力分析Fig.1 Sketch of force of ball bearing

按照Hertz接触理论, 滚动体和滚道的作用力Q₁_j、Q₂_j可以由球/滚道接触趋近量δ ₁_j、δ ₂_j求得。当实际滚道发生挠曲变形后, 第j个滚动体方位角处套圈局部表面偏离理论基圆的距离可以表示为δ ₁_jh、δ ₂_jh。根据小变形假设, 可以将其与滚动体的接触趋近量δ ₁_j、δ ₂_j相叠加, 再考虑接触区间的油膜厚度h₁_j、h₂_j, 得到滚动体与非圆滚道的实际接触趋近量δ '₁_j、δ '₂_j。假设沟曲率系数不变, 进而得到滚动体与非圆滚道的接触载荷Q'₁_j、Q'₂_j。

$\{\begin{array}{l} δ'_{1 j} = δ_{1 j} + h_{1 j} + δ_{1 j h} \\ Q'_{1 j} = {(\frac{2}{ξ_{1 j}^{*}})}^{1.5} \cdot (\frac{2 E_{1}^{*}}{3 (\sum ρ_{1})^{0.5}}) \cdot (δ'_{1 j})^{1.5} \\ δ'_{2 j} = δ_{2 j} + h_{2 j} + δ_{2 j h}^{} \\ Q'_{2 j} = {(\frac{2}{ξ_{2 j}^{*}})}^{1.5} \cdot (\frac{2 E_{2}^{*}}{3 (\sum ρ_{2})^{0.5}}) \cdot (δ'_{2 j})^{1.5} \end{array} (1)$

式中: $E_{1}^{*} 为滚动体 / 外圈等效弹性模量; E_{2}^{*}$ 为滚动体/内圈等效弹性模量; ∑ ρ ₁为滚动体/外圈主平面曲率和; ∑ ρ ₂为滚动体/内圈主平面曲率和; $ξ_{1 j}^{*} 、 ξ_{2 j}^{*}$ 为点接触椭圆积分系数。

油膜厚度采用多重网格法^[16]计算, 该方法考虑了润滑油的黏压黏温和密压密温关系。润滑油拖动系数采用五参数润滑剂流变模型计算, 该模型经过试验验证, 包含了温度及压力对润滑剂流变特性的影响^[17]。

根据非圆套圈的几何形状、滚动体/滚道接触载荷、套圈外载荷得到滚动体平衡方程(见式(2))及套圈平衡方程(见式(3)), 文献[18]给出了保持架平衡方程, 将各平衡方程联立, 得到非圆套圈球轴承的拟动力学模型。

$\begin{array}{l} \{\begin{array}{l} - Q'_{1 j} \sin α_{1 j} + Q'_{2 j} \sin α_{2 j} - f'_{1 j} \cos α_{1 j} + \\ f'_{2 j} \cos α_{1 j} - F_{sr zj} = 0 \\ F_{sr yj} - F_{d} + T_{1 j} - T_{2 j} - f_{st uj} + F_{yj} = 0 \\ - Q'_{1 j} \cos α_{1 j} + Q'_{2 j} \cos α_{2 j} + f'_{1 j} \sin α_{1 j} - \\ f'_{2 j} \sin α_{1 j} - F_{sr zj} + F_{zj} = 0 \\ - 0.5 D_{w} T_{1 j} \cos α_{1 j} - 0.5 D_{w} T_{2 j} \cos α_{2 j} + \\ 0.5 D_{w} f_{st zj} + M_{xj} = 0 \\ - 0.5 D_{w} (f'_{1 j} + f'_{2 j}) + M_{yj} = 0 \\ - 0.5 D_{w} T_{1 j} \sin α_{1 j} - 0.5 D_{w} T_{2 j} \sin α_{2 j} - \\ 0.5 D_{w} f_{st zj} + M_{zj} = 0 \end{array} \\ (2) \end{array}$

$\{\begin{array}{l} F_{x} - \overset{N}{\sum_{j = 1}} (Q_{2 j} \sin α_{2 j} + T'_{2 j} \cos α_{2 j}) = 0 \\ F_{y} - F_{lr} \sin ψ + F_{lt} \cos ψ - \overset{N}{\sum_{j = 1}} (Q_{2 j} \cos α_{2 j} - \\ T'_{2 j} \sin α_{2 j}) \sin φ_{j} = 0 \\ F_{z} - F_{lr} \cos ψ - F_{lt} \sin ψ - \overset{N}{\sum_{j = 1}} (Q_{2 j} \cos α_{2 j} + \\ T'_{2 j} \sin α_{2 j}) \cos φ_{j} = 0 \\ M_{y} - \overset{N}{\sum_{j = 1}} [r_{r 2} (Q_{2 j} \sin α_{2 j} + T'_{2 j} co s α_{2 j}) - \\ f_{2} D_{w} T'_{2 f} \cos α_{2 j}] \cdot \cos φ_{j} = 0 \\ M_{z} - \overset{N}{\sum_{j = 1}} [r_{r 2} (Q_{2 j} \sin α_{2 j} + T'_{2 j} \cos α_{2 j}) - \\ f_{2} D_{w} T'_{2 f} \cos α_{2 j}] \cdot \sin φ_{j} = 0 \end{array} (3)$

式中: $F_{x} 、 F_{y} 、 F_{z} 、 M_{y} 、 M_{z}$ 为施加在轴承内圈上的外部载荷; $α_{1 j} 、 α_{2 j}$ 分别为滚动体与外、内圈的接触角;φ_j为第j号滚动体的圆周方位角;ψ为保持架与内圈接触点的圆周方位角;F_lr为保持架与套圈的法向接触载荷;F_lt为保持架与套圈的切向摩擦力;r_r2为内圈滚道理论沟曲率中心半径。

本模型在考虑了轴承内部接触微区特性、润滑剂流变特性的基础上, 加入了非圆滚道的影响, 能够精确分析球轴承套圈变形后的动态特性及疲劳寿命。

1.2 结构变形的有限元分析模型

鼠笼支撑一体化轴承如图2(a)所示, 鼠笼支撑结构的圆柱段直接作为轴承外圈, 轴承内圈则安装在空心轴上。在ANSYS中建立包含薄壁空心轴、轴承内圈和轴承外圈-鼠笼支撑结构的有限元模型。对装配体进行布尔运算保证其满足六面体网格划分条件, 采用三维实体单元SOLID45单元对其进行网格划分, 如图2(b)所示。

	Figure Option View Download New Window
	图2 鼠笼支撑一体化球轴承FEM模型Fig.2 Preprocess of FEM

轴承外圈与鼠笼支撑结构是一体结构, 不存在结合部耦合问题。轴承内圈与轴之间则存在两个接触对, 轴承内圈内表面与轴的接触, 及内圈侧面与轴肩部位的圆环面接触。分别把内圈内表面、内圈侧面设为接触面(Contact surface), 对应的轴径表面、轴肩面设为目标面(Target surface), 采用TARGE170和CONTA174面-面接触单元描述其相互接触部分, 如图2(c)(d)所示。

轴承中球/滚道接触属于点接触, 通过拟动力学计算各个滚动体分别与内/外滚道接触点的载荷值, 然后在有限元模型中将各个载荷分别施加在内/外滚道对应的接触位置上, 如此处理可以发挥轴承拟动力学及润滑剂流变模型在接触微区计算中的高精度优势, 同时可避免有限元方法在处理跨尺度问题时的求解困难, 如图2(e)所示。

在鼠笼基座端面和轴两端设置位移约束, 求解便可得到鼠笼结构及薄壁套圈的结构弹性变形。求出的滚道施力点的位移即代表了滚动体与滚道接触点的位移, 该位移包含两部分, 一是与套圈在外力作用下沿外力方向的刚体平移, 二是滚道该接触点相对滚道圆心的相对位移即偏离理论基圆的距离δ ₁_jh、δ ₂_jh。由整个结构的对称性, 可以很容易通过竖直方向上的节点位移确定出套圈圆心位移。由此可以分解出滚道施力点相对于滚道几何中心的偏移量δ ₁_jh、δ ₂_jh。

1.3 拟动力学-FEM迭代模型

由FEM模型计算得出的各个球/滚道接触位置上的套圈局部挠曲变形量, 通过式(1)代入到非圆滚道拟动力学模型中。采用非圆滚道的拟动力学修正模型重新计算轴承内部球/滚道载荷, 并将结果作为初始值, 再次施加到有限元模型中, 依此迭代, 直至轴承内部载荷值收敛为止。

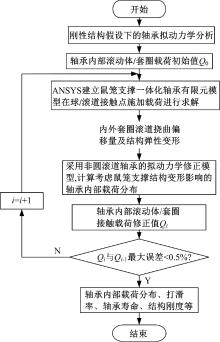
非圆滚道拟动力学-FEM迭代模型分析流程如图3所示。结果收敛后即可得到考虑鼠笼柔性支撑一体化结构的球轴承内部载荷分布及整体结构变形, 进而得到考虑鼠笼刚度的轴承实际刚度、轴承寿命等动态特性。

	Figure Option View Download New Window
	图3 拟动力学-FEM迭代分析流程图Fig.3 Flow chart of quasi dynamic-FEM model

2 结果与讨论

以某型号的鼠笼支撑一体化球轴承为例, 分析鼠笼柔性支撑结构对其承载性能和疲劳寿命的影响。轴承主要参数如表1、表2所示。轴、轴承内圈、球、外圈-鼠笼的工作温度分别为230、220、226、218 ℃。轴承转速为38 000 r/min, 承受径向载荷为1152 N, 轴向载荷为5432 N(包括轴向工作载荷5307 N及预紧力125 N), 采用飞马2号润滑油, 入口油温为110 ℃。

表1 鼠笼支撑一体化球轴承主要参数 Table 1 Parameters of bearing and squirrel structure

表2 鼠笼支撑一体化球轴承主要材料参数 Table 2 Parameters of material of bearing and squirrel structure

采用前述的拟动力学-FEM迭代模型对该轴承进行分析。高温环境中, 在润滑良好的情况下, 认为轴承各部件的温度与环境温度一致, 通过材料的热膨胀系数来反映环境温度下各轴承部件的尺寸变化, 在模型中直接使用考虑热膨胀后的轴承几何尺寸。

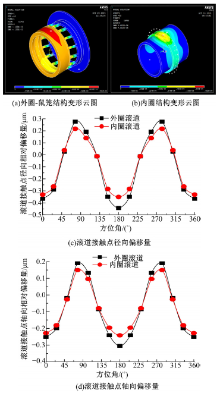
图4(a)(b)为套圈及鼠笼结构的变形云图。外圈圆心沿径向位移达到0.0445 mm, 轴向为0.0124 mm, 而内圈圆心沿径向位移为0.004 89 mm, 轴向为0.0132 mm。为描述套圈的变形, 将滚道接触点相对标准圆形滚道的相对偏移量分解为径向和轴向, 分别在图4(c)(d)中表示出。可以看到, 套圈滚道的变形量远小于套圈的平移量。在方位角0° 和180° 左右, 即径向载荷方向上, 套圈滚道半径表现出扩张趋势, 相应的, 在90° 和270° 左右, 即与径向载荷方向垂直的方向, 套圈受力较小, 因此发生收缩以维持载荷方向上的扩张。

	Figure Option View Download New Window
	图4 结构变形分析结果Fig.4 Deformation of rings and squirrel-cage

在考虑套圈及鼠笼支撑结构变形的影响下, 采用前述的FEM-拟动力学迭代模型计算该轴承的内部载荷分布。采用文献[18, 19]中刚性假设下不考虑套圈及鼠笼支撑结构变形的拟动力学模型计算结果作为对比。轴承内部载荷分布计算结果如图5所示。

	Figure Option View Download New Window
	图5 轴承内部载荷分布对比Fig.5 Contrast of load distribution

由图5可以看出, 相对于刚性结构假设下的计算结果, 在鼠笼柔性支撑结构变形的影响下, 最大球/滚道载荷由841.5 N降低至749.8 N, 减少了10.94%; 载荷在轴承内部分布得更为均匀, 在-52° ~52° 区间里5个承受载荷较大的滚动体上的载荷变小。

图6为轴承各个滚动体的打滑率分布。由于球的打滑率很大程度上取决于球与滚道之间的载荷大小, 因此轴承内部载荷的变化带来了各滚动体打滑率的变化。在球/滚道载荷减小的区间内, 球的打滑率增加, 而在球/滚道载荷增大的区间内, 球打滑率相应会减小。柔性支撑下轴承保持架打滑率相对于刚性支撑, 由4.41%上升至5.11%, 增加了15.8%。

	Figure Option View Download New Window
	图6 鼠笼支撑对球打滑率的影响Fig.6 Distribution of sliding-ratio of balls

图7为轴承保持架打滑率随转速的变化。由于鼠笼柔性支撑结构变形导致轴承内部最大载荷降低, 削弱了对滚动体的拖动力, 导致轴承整体打滑率相对于刚性支撑下变大。

	Figure Option View Download New Window
	图7 鼠笼支撑对轴承保持架打滑率的影响Fig.7 Influence of operation speed on cage sliding

图8为轴承套圈壁厚变化对轴承内部载荷分布的影响。

	Figure Option View Download New Window
	图8 轴承套圈壁厚对鼠笼支撑一体化轴承内部载荷的影响Fig.8 Influence of ring thickness on load distribution

可以看出, 套圈壁厚越大, 轴承内部载荷分布越接近不考虑鼠笼支撑影响的计算结果; 套圈壁厚越小, 鼠笼支撑结构给轴承内部载荷分布带来的影响越显著。

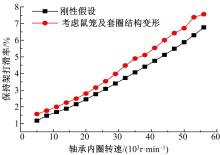
图9为在不同套圈壁厚的情况下依据L-P寿命理论计算出的轴承疲劳寿命值。可以看出, 在刚性假设下, 套圈壁厚对轴承疲劳寿命没有影响; 考虑鼠笼支撑结构变形影响后, 轴承疲劳寿命增加6.35%~11.3%。随着套圈壁厚变大, 轴承疲劳寿命变小, 且越来越接近不考虑鼠笼支撑结构变形影响时的轴承疲劳寿命值。

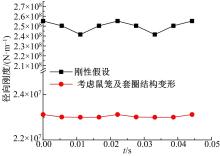
	Figure Option View Download New Window
	图9 套圈壁厚对轴承疲劳寿命的影响Fig.9 Influence of ring thickness on fatigue life

图10为轴承径向刚度, 可以看出, 当考虑鼠笼支撑结构的影响后, 轴承整体径向刚度减小了一个数量级。受滚动体通过频率的影响, 轴承整体刚度呈现周期性变化, 变化幅度由5.63%减小到0.51%。

	Figure Option View Download New Window
	图10 鼠笼柔性支撑结构对轴承径向刚度的影响Fig.10 Influence of flexible support on stiffness

3 结论

(1)本文在轴承拟动力学模型中加入了套圈结构变形的影响, 得到非圆滚道球轴承的拟动力学修正模型, 并与有限元模型相耦合, 建立了考虑结构变形的鼠笼柔性支撑一体化轴承的拟动力学-FEM迭代分析模型。

(2)对一个鼠笼支撑一体化球轴承的分析表明, 相对于刚性支撑情况下, 鼠笼支撑结构能够有效减小轴承内部最大接触载荷, 使轴承内部载荷分布更加均匀, 并延长轴承疲劳寿命, 但是轴承整体打滑会少许上升。

(3)采用这一模型分析了轴承外圈壁厚对轴承动态性能的影响。结果表明, 轴承套圈壁厚越厚, 计算结果越接近刚性支撑假设的计算结果; 轴承套圈壁厚越薄, 鼠笼支撑带来的影响越显著。

(4)鼠笼支撑一体化结构会显著减小轴承刚度, 但是轴承整体打滑会少许上升, 因此在高速轴系中采用鼠笼支撑结构时, 需要综合考虑轴承承载性能、整体结构刚度、打滑率等因素, 与轴系设计要求相结合, 选择恰当的鼠笼结构, 使得轴承刚度及疲劳寿命得到优化, 同时确保打滑率仍然能够满足要求。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	毛宇泽, 王黎钦, 古乐. 负游隙对高速高温薄壁圆柱滚子轴承动态性能的影响分析[J]. 航空动力学报, 2016, 31(11): 2795-2800. Mao Yu-ze, Wang Li-qin, Gu Le. Influence of negative clearance on loading characteristics and fatigue life of cylindrical roller bearings[J]. Journal of Aerospace Power, 2016, 31(11): 2795-2800. [本文引用:1]
[2]	Franz-Josef E. An overview of performance characteristics, experiences and trends of aerospace engine bearings technologies[J]. Chinese Journal of Aeronautics, 2007, 20: 378-384. [本文引用:1]
[3]	Harris T A. Prediction of ball fatigue life in a ball/V-ring test rig[J]. J Tribol, 1997, 119: 365-374. [本文引用:1]
[4]	崔立, 王黎钦, 郑德志. 航空发动机高速滚子轴承动态特性分析[J]. 航空学报, 2008, 29(2): 492-498. Cui Li, Wang Li-qin, Zheng De-zhi. Analysis on dynamic characteristics of aero-engine high-speed roller bearings[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(2): 492-498. [本文引用:1]
[5]	Pinel S I, Signer H R, Zaretsky E V. Design and operating characteristics of high-speed, small-bore ball bearings[J]. Tribology Transactions, 1998, 41(4): 423-434. [本文引用:1]
[6]	Adatepe H, Biyiklioglu A, Sofuoglu H. An investigation of tribological behaviors of dynamically loaded non-grooved and micro-grooved journal bearings[J]. Tribology International, 2013, 58: 12-19. [本文引用:1]
[7]	Oswald F B, Zaretsky E V, Poplawski J V. Interference-fit life factors for ball bearings[J]. Tribology Transactions, 2010, 54(1): 1-20. [本文引用:1]
[8]	Harris T A, Broschard J L. Analysis of an improved planetary gear transmission bearing[J]. Journal of Fluids Engineering, 1964, 86(3): 457-461. [本文引用:1]
[9]	沈允文, 张同卿, 李树庭, 等. 柔性滚动轴承的振动分析[J]. 机械科学与技术, 1995(5): 1-6. Shen Yun-wen, Zhang Tong-qing, Li Shu-ting, et al. Vibration analysis of flexible rolling bearing[J]. Mechanical Science and Technology for Aerospace Engineering, 1995(5): 1-6. [本文引用:1]
[10]	Yao T, Chi Y, Huang Y. Research on flexibility of bearing rings for multibody contact dynamics of rolling bearings[J]. Procedia Engineering, 2012, 31: 586-594. [本文引用:1]
[11]	Amasorrain J I, Sagartzazu X, Damian J. Load distribution in a four contact-point slewing bearing[J]. Mechanism and Machine Theory, 2003, 38(6): 479-496. [本文引用:1]
[12]	Kania L. Modelling of rollers in calculation of slewing bearing with the use of finite elements[J]. Mechanism and Machine Theory, 2006, 41(11): 1359-1376. [本文引用:1]
[13]	Olave M, Damian J, Serna A, et al. Design of four contact-point slewing bearing with a new load distribution procedure to account for structural stiffness[J]. Journal of Mechanical Design, 2010, 132(2): 021006. [本文引用:1]
[14]	Shu Ju, Wang Li-qin, Mao Yu-ze, et al. Iterative FEA method for load distribution of flexible supporting thin-section ball bearing[J]. Journal of Harbin Institute of Technology, 2015, 22(1): 9-14. [本文引用:1]
[15]	Ni Y, Liu W, Deng S, et al. Performance analysis of thin wall angular contact ball bearings considering the ferrule deformation[J]. Journal of Aerospace Power, 2010, 25(6): 1432-1436. [本文引用:1]
[16]	史修江, 王黎钦, 郑德志. 考虑动力学特性的航空发动机主轴球轴承热弹流分析[J]. 摩擦学学报, 2015, 35(4): 415-422. Shi Xiu-jiang, Wang Li-qin, Zheng De-zhi. Thermal EHL analysis of aero-engine mainshaft ball bearing with dynamic characteristics[J]. Tribology, 2015, 35(4): 415-422. [本文引用:1]
[17]	Wang Y S, Yang B Y, Wang L Q. Investigation into the traction coefficient in elastohydrodynamic lubrication[J]. Tribotest, 2004, 11(2): 113-124. [本文引用:1]
[18]	崔立, 王黎钦, 郑德志. 高速球轴承打滑的临界负荷研究[J]. 航空动力学报, 2007, 11(3): 1971-1976. Cui Li, Wang Li-qin, Zheng De-zhi. Study on critical load of skidding in high speed ball bearing[J]. Journal of Aerospace Power, 2007, 11(3): 1971-1976. [本文引用:1]
[19]	侯萍萍, 王黎钦, 柏迎村, 等. 填脂量对高速电主轴轴承性能的影响[J]. 吉林大学学报: 工学版, 2017, 47(2): 518-523. Hou Ping-ping, Wang Li-qin, Bai Ying-cun, et al. Effect of grease filling amount on the performance of bearing in high speed motorized spindle[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(2): 518-523. [本文引用:1]

2016

0.0

... 鼠笼支撑一体化轴承正在逐渐成为航空航天轴承领域的技术趋势^[1,2] ...

2007

0.0

... 鼠笼支撑一体化轴承正在逐渐成为航空航天轴承领域的技术趋势^[1,2] ...

1997

0.0