具有区间时变时滞的线性系统稳定性分析

引用本文

闫冬梅, 钟辉, 任丽莉, 王若琳, 李红梅. 具有区间时变时滞的线性系统稳定性分析[J].吉林大学学报（工学版）, 2018,48(5): 1556-1562
YAN Dong-mei, ZHONG Hui, REN Li-li, WANG Ruo-lin, LI Hong-mei. Stability analysis of linear systems with interval time-varying delay[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1556-1562 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20180320
Permissions

具有区间时变时滞的线性系统稳定性分析

闫冬梅¹, 钟辉¹, 任丽莉², 王若琳³, 李红梅¹

1.吉林大学大数据和网络管理中心,长春 130012

2.长春师范大学网络中心,长春 130032

3.吉林交通职业技术学院管理工程学院,长春 130012

通信作者:钟辉(1979-),男,副研究员,博士研究生.研究方向:通信与信息系统.E-mail:zhongh@jlu.edu.cn

作者简介:闫冬梅(1978-),女,高级工程师.研究方向:网络系统管理与控制.E-mail:yandongm@jlu.edu.cn

基金:吉林省省级产业创新专项项目(2017C031-4)

摘要

研究了给定区间时变时滞线性系统的稳定性问题。通过构造一个具有三重积分项的新的Lyaounov-Krasovskii泛函,利用一个最新提出的基于自由矩阵的积分不等式,得到了新的保守性更小的保证系统稳定的充分条件。最后,通过2个实例验证了所提出的方法比现有方法具有更小的保守性。

关键词: 自动控制技术; 时滞系统; 时滞依赖稳定性; 区间时滞; 线性矩阵不等式

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2018)05-1556-07

Stability analysis of linear systems with interval time-varying delay

YAN Dong-mei¹, ZHONG Hui¹, REN Li-li², WANG Ruo-lin³, LI Hong-mei¹

1.Management Center of Big Data and Network, Jilin University, Changchun 130012,China

2.Network Center, Changchun Normal University, Changchun 130032,China

3.College of Administrative Engineering,Jilin Communications Polytechnic, Changchun 130012,China

Abstract

This paper investigates the stability problem of a linear system with time-varying delay. The time-varying delay is assumed to belong to a given interval. A new Lyapunov-Krasovskii function is constructed which contains some tripe integral terms. Using some integral inequalities including the recent proposed free-matrix-based integral inequality, new sufficient stability conditions are obtained, which are presented in terms of Linear Matrix Inequality (LMI). Finally, two examples are given to demonstrate that the obtained results are less conservative than some existing method.

Keyword: automatic control technology; time-delay system; delay-dependent stability; interval delay; linear matrix inequality

文章图片

0 引言

时滞现象存在于许多实际系统中, 例如化工控制过程, 网络化控制系统^{[1, 2]}。时滞是引起系统不稳定和使系统性能恶化的主要原因之一^[3]。近年来, 由于其在理论和实际应用中的重要性, 具有区间时变时滞的线性系统的稳定性分析问题得到了越来越多的关注。一般来说, 研究时滞系统稳定性分析有两类方法。一类是频域法, 另一类是时域法。频域法通常只适用于定常时滞系统, 而在许多实际系统中时滞通常是时变的。例如, 在网络化控制系统中, 从传感器到控制器或者从控制器到执行器的时滞往往是时变的。因此, 时域法被广泛用于研究时变时滞系统的稳定性条件。通过建立一个Lyapunov-Krasovskii泛函或者一个Lyapunov-Razumikhin函数, 可以得到一些更容易验证的充分条件。

现有文献中提出了一些典型的基于Lyapunov泛函的稳定性分析方法。文献[4, 5]提出了广义系统模型变换的方法, 并且证明了广义系统模型变换方法比其他3种模型变换方法更有效。文献[6, 7, 8, 9, 10]提出了自由权矩阵的方法。这种方法比广义系统模型变换方法具有较小的保守性, 因为它不涉及任何模型变换和交叉项的缩放技术。文献[11, 12]提出了一个包含三重积分项的Lyapunov泛函。这个Lyapunov泛函恰当地利用了时滞的下界信息, 因而可以得到具有更小保守性的结果。文献[13]提出了Jesen不等式并将其应用于时滞系统的稳定性分析。与广义系统模型变换方法和自由权矩阵方法相比, Jesen不等式方法涉及的矩阵变量较少, 因此运算效率高。文献[14]提出了一个基于Wirtinger积分不等式的方法, 用该不等式可以得到比运用Jesen不等式保守性更小的稳定性条件。文献[15]提出了凸组合技术。文献[16]提出了倒凸组合方法用来估计Lyaounov泛函的导数, 并且得到了具有更小保守性的结果。除了上面提到的方法, 还有许多其他的方法, 例如文献[17]中的离散Lyapunov泛函方法, 文献[18, 19, 20]中的时滞分割方法等。这些方法的详情可参阅文献[21, 22, 23, 24, 25]。

在现有的文献中, 针对如何减少稳定性条件的保守性主要有两类方法。一个是构造适当的泛函, 另一个是找到新的方法来尽可能紧地估计Lyapunov泛函的导数。本文通过构造一个新的Lyapunov泛函, 并且利用最新提出的基于自由权矩阵的积分不等式方法来估计Lyapunov泛函的导数, 得到了保守性更小的稳定性条件。最后, 通过实例验证了本文提出方法的有效性。

1 理论推导

考虑如下具有区间时变时滞的线性系统:

$\{\begin{array}{l} \overset{\cdot}{x} (t) = Ax (t) + A_{1} x (t - d (t)), t \geq 0 \\ x (θ) = φ (θ), θ \in [- h_{2}, 0] \end{array} (1)$

式中: $x (t) \in R^{n}$ 为状态向量; $A \in R^{n \times n}$ 和 $A_{1} \in R^{n \times n}$ 均为系统矩阵; 初始条件 $φ (θ)$ 为一个连续可微的函数; $d (t)$ 为可微函数且满足:

$\{\begin{array}{l} 0 < h_{1} \leq d (t) \leq h_{2} \\ μ_{1} \leq \overset{\cdot}{d} (t) \leq μ_{2} \end{array} (2)$

式中: $0 < h_{1} \leq h_{2}$ 和 $μ_{1} \leq μ_{2}$ 为已知常数。

以下研究在时滞满足式(2)的情况下, 针对系统提出具有更小保守性的稳定性条件。

引理1^[22] $x$ 是一个可微的向量函数。对于正定对称矩阵 $R \in R^{n \times n} > 0, X_{1} \in R^{3 n \times 3 n} > 0,$ 和 $X_{3} \in R^{3 n \times 3 n} > 0,$ 以及任意适当维数的矩阵 $X_{2} \in R^{3 n \times 3 n}, N_{1} \in R^{3 n \times n}, N_{2} \in R^{3 n \times n},$ 使得:

$[\begin{array}{l} X_{1} & X_{2} & N_{1} \\ * & X_{3} & N_{2} \\ * & * & R \end{array}] \geq 0$

那么下面的积分不等式成立:

$- \int_{t}^{-} {\overset{\cdot}{x}}^{t} (s) R \overset{\cdot}{x} (s) d s \leq φ (t) Ξφ (t) (3)$

式中:

$φ (t) = [x (t - a) x (t - b) \frac{1}{b - a} \int_{t}^{-} x (s) d s],$

$\begin{array}{l} Ξ = (b - a) (X_{1} + \frac{1}{3} Z_{3}) + N_{1} Π_{1} + {Π^{T}}_{1} {N^{T}}_{1} + \\ N_{2} Π_{2} + {Π^{T}}_{2} {N^{T}}_{2}, \end{array}$

$Π_{1} = [I - I 0], Π_{2} = [- I - I 2 I] 。$

引理2^{[11, 13]} 对于一个矩阵 $Z \in R^{n \times n} > 0,$ 和参数 $τ_{2} > τ_{1} > 0,$ 下面的两个积分不等式成立:

$\begin{array}{l} - τ_{12} \int_{t}^{-} x^{T} (s) Zx (s) d s \leq \\ - \int_{t}^{-} x^{T} (s) d sZ \int_{t}^{-} x (s) d s, \\ - \frac{τ_{12}^{2}}{2} \int_{-}^{τ_{2}} \int_{t}^{+} x^{T} (s) Zx (s) d s d θ \leq \\ - \int_{-}^{τ_{2}} \int_{t}^{+} x^{T} (s) d s d θZ \int_{-}^{τ_{2}} \int_{t}^{+} x (s) d s d θ \end{array}$

式中: $τ_{12} = τ_{2} - τ_{1} 。$

下面的定理1给出了保证系统(1)(2)渐近稳定的充分条件。

定理1 对于给定的标量 $h_{1} 、 h_{2} 、 μ_{1} 、 μ_{2},$ 如果存在矩阵 $P \in R^{7 n \times 7 n} > 0; Q_{i} \in R^{2 n \times 2 n} > 0; S_{i} \in R^{2 n \times 2 n} > 0; R_{i} \in R^{n \times n} > 0; i = 1, 2; Z_{j} \in R^{n \times n} > 0; j = 1, 2, 3, 4;$ 对称矩阵 $X_{1}, X_{3}, G_{1}, G_{3}, L_{1}, L_{3} \in R^{3 n \times 3 n},$ 和任意矩阵 $X_{2}, G_{2}, L_{2} \in R^{3 n \times 3 n}; N_{1}, N_{2}, M_{1}, M_{2}, W_{1}, W_{2} \in R^{3 n \times n},$ 使得下面的线性矩阵不等式对于 $d (t) = {h_{1}, h_{2}}$ 和 $\overset{\cdot}{d} (t) = {μ_{1}, μ_{2}}$ 成立, 则系统 (1)(2)渐近稳定。

$\begin{array}{l} Ψ (d (t), \overset{\cdot}{d} (t)) < 0 (4) \\ [\begin{array}{l} X_{1} & X_{2} & N_{1} \\ * & X_{3} & N_{2} \\ * & * & Z_{1} \end{array}] \geq 0 (5) \\ [\begin{array}{l} G_{1} & G_{2} & M_{1} \\ * & G_{3} & M_{2} \\ * & * & Z_{2} \end{array}] \geq 0 (6) \\ [\begin{array}{l} L_{1} & L_{2} & W_{1} \\ * & L_{3} & W_{2} \\ * & * & Z_{2} \end{array}] \geq 0 (7) \end{array}$

式中:

$\begin{array}{l} Ψ (d (t), \overset{\cdot}{d} (t)) = H_{1} P H_{2} + {H^{T}}_{2} P {H^{T}}_{1} + H_{3} (S_{1} - \\ Q_{1} + Q_{2}) {H^{T}}_{3} + H_{4} (1 - \overset{\cdot}{d} (t)) (S_{2} - S_{1}) {H^{T}}_{4} + \\ H_{5} (- S_{2} - Q_{2}) {H^{T}}_{5} + H_{6} Q_{1} {H^{T}}_{6} + {A^{T}}_{b} Θ A_{b} + \\ e_{6} Λ {e^{T}}_{6} + h_{1} e_{1} Z_{3} {e^{T}}_{1} + h_{12} e_{3} Z_{4} {e^{T}}_{3} + H_{7} Ω_{1} {H^{T}}_{7} + \\ H_{8} Ω_{2} {H^{T}}_{8} + H_{9} Ω_{3} {H^{T}}_{9} - h_{1} e_{8} Z_{3} {e^{T}}_{8} - \\ α e_{9} Z_{4} {e^{T}}_{9} - β e_{10} Z_{4} {e^{T}}_{10} - 2 (e_{1} - e_{8}) R_{1} (e_{1} - \\ e_{8})^{T} - 2 (e_{2} - e_{10}) R_{2} (e_{2} - e_{10})^{T} - 2 (e_{3} - \\ e_{9}) R_{2} (e_{3} - e_{9})^{T}, \end{array}$

$H_{1} = [e_{1} e_{2} e_{3} e_{4} α e_{9} β e_{10} h_{1} e_{8}],$

$\begin{array}{l} H_{2} = [\begin{array}{l} A_{b} \\ (1 - \overset{\cdot}{d} (t)) {e^{T}}_{5} \\ {e^{T}}_{6} \\ {e^{T}}_{7} \\ {e^{T}}_{3} - (1 - \overset{\cdot}{d} (t)) {e^{T}}_{2} \\ (1 - \overset{\cdot}{d} (t)) {e^{T}}_{2} - {e^{T}}_{4} \\ {e^{T}}_{1} - {e^{T}}_{3} \end{array}], H_{3} = [e_{3} e_{6}], \\ H_{4} = [e_{2} e_{5}], \end{array} H_{5} = [e_{4} e_{7}],$

$H_{6} = [e_{1} {A^{T}}_{b}], H_{7} = [e_{1} e_{3} e_{8}], H_{8} = [e_{3} e_{2} e_{9}],$

$\begin{array}{l} H_{9} = [e_{2} e_{4} e_{10}], Θ = h_{1} Z_{1} + \frac{1}{2} h_{1}^{2} R_{1}, \\ Λ = h_{12} Z_{2} + \frac{1}{2} h_{12}^{2} R_{2}, \end{array}$

$A_{b} = [A A_{1} 00000000],$

$\begin{array}{l} Ω_{1} = h_{1} (X_{1} + \frac{1}{3} X_{3}) + N_{1} Π_{1} + {Π^{T}}_{1} {N^{T}}_{1} + \\ N_{2} Π_{2} + {Π^{T}}_{2} {N^{T}}_{2}, \end{array}$

$\begin{array}{l} Ω_{2} = α (G_{1} + \frac{1}{3} G_{3}) + M_{1} Π_{1} + {Π^{T}}_{1} {M^{T}}_{1} + \\ M_{2} Π_{2} + {Π^{T}}_{2} {M^{T}}_{2}, \end{array}$

$\begin{array}{l} Ω_{3} = β (L_{1} + \frac{1}{3} L_{3}) + W_{1} Π_{1} + {Π^{T}}_{1} {W^{T}}_{1} + \\ W_{2} Π_{2} + {Π^{T}}_{2} {W^{T}}_{2}, \end{array}$

$α = d (t) - h_{1}, β = h_{2} - d (t),$

${e^{T}}_{i} = [\underset{i - 1}{\underset{︷}{0 \dots 0}} I \underset{10 - i}{\underset{︷}{0 \dots 0}}], (i = 1, 2, \dots, 10) 。$

证明:选择如下Lyapunov泛函:

$\begin{array}{l} V (x_{t}) = ζ^{T} (t) Pζ (t) + \int_{t}^{-} η^{T} (s) S_{1} η (s) d s + \\ \int_{t}^{-} η^{T} (s) S_{2} η (s) d s + \\ \int_{t}^{-} η^{T} (s) Q_{1} η (s) d s + \\ \int_{t}^{-} η^{T} (s) Q_{2} η (s) d s + \\ \int_{-}^{h_{1}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) Z_{1} \overset{\cdot}{x} (s) d s d θ + \\ \int_{-}^{h_{2}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) Z_{2} \overset{\cdot}{x} (s) d s d θ + \\ \int_{-}^{h_{1}} \int_{t}^{+} x^{T} (s) Z_{3} x (s) d s d θ + \\ \int_{-}^{h_{2}} \int_{t}^{+} x^{T} (s) Z_{4} x (s) d s d θ + \\ \int_{-}^{h_{1}} \int_{θ}^{0} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{1} \overset{\cdot}{x} (s) d s d λ d θ + \\ \int_{-}^{h_{2}} \int_{θ}^{-} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) d s d λ d θ (8) \end{array}$

沿系统(1)的轨迹对Lyapunov泛函(8)求导, 可得:

$\begin{array}{l} \overset{\cdot}{V} (x_{t}) = 2 ζ^{T} (t) P \overset{\cdot}{ζ} (t) + η^{T} (t - h_{1}) S_{1} η (t - h_{1}) - \\ (1 - \overset{\cdot}{d} (t)) η^{T} (t - d (t)) S_{1} η (t - d (t)) + \\ (1 - \overset{\cdot}{d} (t)) η^{T} (t - d (t)) S_{2} η (t - d (t)) - \\ η^{T} (t - h_{2}) S_{2} η (t - h_{2}) + \\ η^{T} (t) Q_{1} η (t) - η^{T} (t - h_{1}) Q_{1} η (t - h_{1}) + \\ η^{T} (t - h_{1}) Q_{2} η (t - h_{1}) - η^{T} (t - h_{2}) Q_{2} η (t - \\ h_{2}) + h_{1} {\overset{\cdot}{x}}^{T} (t) Z_{1} \overset{\cdot}{x} (t) - \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) Z_{1} \overset{\cdot}{x} (s) d s + \\ h_{12} {\overset{\cdot}{x}}^{T} (t - h_{1}) Z_{2} \overset{\cdot}{x} (t - h_{1}) - \\ \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) Z_{2} \overset{\cdot}{x} (s) d s + \\ h_{1} x^{T} (t) Z_{3} x (t) - \int_{t}^{-} x^{T} (s) Z_{3} x (s) d s + \\ h_{12} x^{T} (t - h_{1}) Z_{4} x (t - h_{1}) - \\ \int_{t}^{-} x^{T} (s) Z_{4} x (s) d s + \\ \frac{h_{1}^{2}}{2} {\overset{\cdot}{x}}^{T} (t) R_{1} \overset{\cdot}{x} (t) - \int_{-}^{h_{1}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{1} \overset{\cdot}{x} (s) d s d θ + \\ \frac{h_{12}^{2}}{2} {\overset{\cdot}{x}}^{T} (t - h_{1}) R_{2} \overset{\cdot}{x} (t - h_{1}) - \\ \int_{-}^{h_{2}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) d s d θ \end{array} (9)$

式中:

$h_{12} = h_{2} - h_{1},$

$\begin{array}{l} ζ (t) = col \{\frac{}{} x (t), x (t - d (t)), x (t - h_{1}), \\ x (t - h_{2}), \int_{t}^{-} x (s) d s, \int_{t}^{-} x (s) d s, \int_{t}^{-} x (s) d s\}, \end{array}$

$η (t) = col \{x (t), \overset{\cdot}{x} (t)\} 。$

利用引理1, 可得:

$\begin{array}{l} - \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) Z_{1} \overset{\cdot}{x} (s) d s \leq ξ^{T} (t) H_{7} Ω_{1} {H^{T}}_{7} ξ (t) (10) \\ 和 \\ - \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) Z_{2} \overset{\cdot}{x} (s) d s = \\ - \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) Z_{2} \overset{\cdot}{x} (s) d s - \int_{t}^{-} {\overset{\cdot}{x}}^{T} (s) Z_{2} \overset{\cdot}{x} (s) d s \leq \\ ξ^{T} (t) (H_{8} Ω_{2} {H^{T}}_{8} + H_{9} Ω_{3} {H^{T}}_{9}) ξ (t) (11) \end{array}$

式中:

$\begin{array}{l} ξ (t) = col \{\frac{}{} x (t), x (t - d (t)), x (t - h_{1}), \\ x (t - h_{2}), \overset{\cdot}{x} (t - d (t)), \overset{\cdot}{x} (t - h_{1}), \\ \overset{\cdot}{x} (t - h_{2}), \frac{1}{h} \int_{t}^{-} x (s) d s, \\ \frac{1}{d (t) - h_{1}} \int_{t}^{-} x (s) d s, \frac{1}{h_{2} - d (t)} \int_{t}^{-} x (s) d s\} \end{array}$

利用引理2, 可得:

$\begin{array}{l} - \int_{t}^{-} x^{T} (s) Z_{3} x (s) d s \leq - h_{1} ξ^{T} (t) e_{8} Z_{3} {e^{T}}_{8} ξ (t) (12) \\ 和 \\ \begin{array}{l} - \int_{-}^{h_{1}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{1} \overset{\cdot}{x} (s) d s d θ \leq \\ - 2 ξ^{T} (t) (e_{1} - e_{8}) R_{1} ({e^{T}}_{1} - {e^{T}}_{8}) ξ (t) \end{array} \\ (13) \\ 显见 : \\ - \int_{t}^{-} x^{T} (s) Z_{4} x (s) d s = \\ - \int_{t}^{-} x^{T} (s) Z_{4} x (s) d s - \int_{t}^{-} x^{T} (s) Z_{4} x (s) d s - \\ \int_{-}^{h_{2}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) d s d θ \leq \\ - \int_{-}^{h_{2}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) d s d θ - \\ \int_{-}^{d} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) d s d θ (14) \end{array}$

利用引理2, 则有:

$\begin{array}{l} - \int_{-}^{d} x^{T} (s) Z_{4} x (s) d s \leq - α ξ^{T} (t) e_{9} Z_{4} {e^{T}}_{9} ξ (t) (15) \\ - \int_{-}^{h_{2}} x^{T} (s) Z_{4} x (s) d s \leq \\ - β ξ^{T} (t) e_{10} Z_{4} {e^{T}}_{10} ξ (t) (16) \\ - \int_{-}^{d} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) d s d θ \leq \\ - 2 ξ^{T} (t) (e_{3} - e_{9}) R_{2} (e_{3} - e_{9})^{T} ξ (t) (17) \\ - \int_{-}^{h_{2}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) d s d θ \leq \\ - 2 ξ^{T} (t) (e_{2} - e_{10}) R_{2} (e_{2} - e_{10})^{T} ξ (t) (18) \end{array}$

由式(9)~(18)可以得到:

$\overset{\cdot}{V} (x_{t}) \leq ξ^{T} (t) Ψ (d (t), \overset{\cdot}{d} (t)) ξ (t) (19)$

由于 $Ψ (d (t), \overset{\cdot}{d} (t)) 、 \overset{\cdot}{d} (t)$ 是关于 $d (t)$ 和 $\overset{\cdot}{d} (t)$ 的线性函数, 可以得到如果

$Ψ |_{d (t) = h_{1}, \overset{\cdot}{d} (t) = μ_{1}} < 0, Ψ |_{d (t) = h_{1}, \overset{\cdot}{d} (t) = μ_{2}} < 0, Ψ |_{d (t) = h_{2}, \overset{\cdot}{d} (t) = μ_{1}} < 0, Ψ |_{d (t) = h_{2}, \overset{\cdot}{d} (t) = μ_{2}} < 0,$

那么 $Ψ (d (t), \overset{\cdot}{d} (t)) < 0, 即 \overset{\cdot}{V} (x_{t}) < 0 。$ 因此, 系统是渐近稳定的。证毕。

需要注意的是, 本文构造了一个包含三重积分的新的Lyapunov泛函。如文献[11, 12]所指出, 这个Lyapunov泛函对于减小结果的保守性是相当有效的。另外, 本文应用文献中最新提出的基于自由矩阵的积分不等式估计Lyapunov泛函的导数, 故能更进一步地减少所得稳定性条件的保守性。正是由于利用了这些新技术, 本文得到的稳定性条件比现有文献中的结果具有更小的保守性。

当时滞变化率未知时, 基于定理1可以得到下面的结论。

定理2 对于给定的标量 $h_{1} 、 h_{2},$ 如果存在矩阵 $P \in R^{4 n \times 4 n} > 0; Q_{i} \in R^{2 n \times 2 n} > 0; R_{i} \in R^{n \times n}; i = 1, 2; Z_{j} \in R^{n \times n} > 0; j = 1, 2, 3, 4;$ 对称矩阵 $X_{1} 、 X_{3} 、 G_{1} 、 G_{3} 、 L_{1} 、 L_{3} \in R^{3 n \times 3 n},$ 和任意适当维数的矩阵 $X_{2} 、 G_{2} 、 L_{2} \in R^{3 n \times 3 n}; N_{1} 、 N_{2} 、 M_{1} 、 M_{2} 、 W_{1} 、 W_{2} \in R^{3 n \times n},$ 使得下面的线性矩阵不等式对 $d (t) = {h_{1}, h_{2}}$ 成立, 则系统(1)(2)渐近稳定。

$\begin{array}{l} \hat{Ψ} (d (t)) < 0 (20) \\ [\begin{array}{l} X_{1} & X_{2} & N_{1} \\ * & X_{3} & N_{2} \\ * & * & Z_{1} \end{array}] \geq 0 (21) \\ [\begin{array}{l} G_{1} & G_{2} & M_{1} \\ * & G_{3} & M_{2} \\ * & * & Z_{2} \end{array}] \geq 0 (22) \\ [\begin{array}{l} L_{1} & L_{2} & W_{1} \\ * & L_{3} & W_{2} \\ * & * & Z_{2} \end{array}] \geq 0 (23) \end{array}$

式中:

$\begin{array}{l} \hat{Ψ} (d (t)) = {\hat{H}}_{1} P {\hat{H}}_{2} + {\hat{H}}^{T}_{2} P {\hat{H}}^{T}_{1} + H_{3} (S_{1} - Q_{1} + \\ Q_{2}) {H^{T}}_{3} - H_{5} Q_{2} {H^{T}}_{5} + H_{6} Q_{1} {H^{T}}_{6} + {A^{T}}_{b} Θ A_{b} + \\ e_{6} Λ {e^{T}}_{6} + h_{1} e_{1} Z_{3} {e^{T}}_{1} + h_{12} e_{3} Z_{4} {e^{T}}_{3} + H_{7} Ω_{1} {H^{T}}_{7} + \\ H_{8} Ω_{2} {H^{T}}_{8} + H_{9} Ω_{3} {H^{T}}_{9} - h_{1} e_{8} Z_{3} {e^{T}}_{8} - α e_{9} Z_{4} {e^{T}}_{9} - \\ β e_{10} Z_{4} {e^{T}}_{10} - 2 (e_{1} - e_{8}) R_{1} (e_{1} - e_{8})^{T} - 2 (e_{2} - \\ e_{10}) R_{2} (e_{2} - e_{10})^{T} - 2 (e_{3} - e_{9}) R_{2} (e_{3} - e_{9})^{T}, \end{array}$

$H_{1} = [e_{1} e_{3} e_{4} h_{1} e_{8}], H_{2} = [A_{b} {e^{T}}_{6} {e^{T}}_{7} {e^{T}}_{1} - {e^{T}}_{3}]^{T} 。$

证明:构造如下Lyapunov泛函:

$\begin{array}{l} V (x_{t}) = {\hat{ζ}}^{T} (t) P \hat{ζ} (t) + \int_{t}^{-} η^{T} (s) Q_{1} η (s) d s + \\ \int_{t}^{-} η^{T} (s) Q_{2} η (s) d s + \\ \int_{-}^{h_{1}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) Z_{1} \overset{\cdot}{x} (s) d s d θ + \\ \int_{-}^{h_{2}} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) Z_{2} \overset{\cdot}{x} (s) d s d θ + \\ \int_{-}^{h_{1}} \int_{t}^{+} x^{T} (s) Z_{3} x (s) d s d θ + \\ \int_{-}^{h_{2}} \int_{t}^{+} x^{T} (s) Z_{4} x (s) d s d θ + \\ \int_{-}^{h_{1}} \int_{θ}^{0} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{1} \overset{\cdot}{x} (s) d s d λ d θ + \\ \int_{-}^{h_{2}} \int_{θ}^{-} \int_{t}^{+} {\overset{\cdot}{x}}^{T} (s) R_{2} \overset{\cdot}{x} (s) d s d λ d θ (24) \end{array}$

式中: $\hat{ζ} (t) = col {x (t), x (t - h_{1}), x (t - h_{2}), \int_{t}^{-} x (s) d s}, η (t) = col {x (t), \overset{\cdot}{x} (t)} 。$ 证明过程与定理1类似, 故从略。证毕。

2 实例验证

本文将通过2个数值仿真示例来验证提出方法的有效性。

例1 考虑具有如下参数的时滞系统:

$A = [\begin{array}{l} - 2 & 0 \\ 0 & - 0.9 \end{array}], A_{1} = [\begin{array}{l} - 1 & 0 \\ - 1 & - 1 \end{array}]$

对于变量 $μ_{2} = - μ_{1} = μ$ 和 $h_{1} = 1,$ 对于给定的时滞下界, 表1列举了使用新方法得到的最大时滞上界, 并与文献[11, 12, 14, 22]中的结果进行了对比。可见, 通过新方法得到的最大时滞上界明显大于文献[11, 12, 14, 22]中的结果, 从而验证了本文提出方法的有效性。

表1 不同μ 得到的最大时滞上界 Table 1 MUDBs for different μ

方法	$μ = 0.1$	$μ = 0.2$	$μ = 0.5$
文献[11]	4.193	3.547	2.305
文献[12]	4.234	3.587	2.438
文献[14]	4.706	3.839	2.423
文献[22]	4.788	4.060	3.055
定理1	4.858	4.136	3.107

表1 不同μ 得到的最大时滞上界 Table 1 MUDBs for different μ

如果时滞变化率不在一个对称区间内, 对于 $h_{1} = 1$ 以及不同的时滞变化率区间的情况, 表2对比了本文得到的最大时滞上界以及文献[14, 22]的结果。在表2中, $[a, b]$ 是指 $a \leq \overset{\cdot}{d} (t) \leq b 。$ 从表2可以看出, 使用新方法可以得到较大的最大时滞上界, 从而说明本文提出的方法具有较小的保守性。

表2 不同时滞变化率区间的最大时滞上界 Table 2 MUBDs for asymmetric delay-rate interval

方法	$[- 0.50.1]$	$[00.1]$	$[- 0.50.2]$	$[00.2]$
文献[14]	4.705	4.706	3.838	3.839
文献[22]	4.710	5.825	3.845	5.685
定理2	4.766	6.004	3.898	5.927

表2 不同时滞变化率区间的最大时滞上界 Table 2 MUBDs for asymmetric delay-rate interval

例2 考虑具有如下参数的时滞系统:

$A = [\begin{array}{l} 0 & 1 \\ - 1 & - 2 \end{array}], A_{1} = [\begin{array}{l} 0 & 0 \\ - 1 & 1 \end{array}]$

对于给定的 $h_{1} = 0.5, μ_{2} = 0.3$ 和不同的 $μ_{1},$ 表3对比了利用本文提出方法得到的最大时滞上界以及文献[11, 12, 14]中的结果。从表3可以看出, 本文提出的方法与文献[11, 12, 14]相比具有更小的保守性。

表3 不同μ ₁得到的最大时滞上界 Table 3 MUBDs for defferent μ ₁

方法	$μ_{1} = - 1$	$μ_{1} = - 0.5$	$μ_{1} = - 0.1$
文献[11]	2.285	2.285	2.285
文献[12]	2.410	2.410	2.410
文献[14]	2.404	2.407	2.417
定理2	2.617	2.674	7.159

表3 不同μ ₁得到的最大时滞上界 Table 3 MUBDs for defferent μ ₁

例3 考虑如下的直流电机系统 :

$\overset{\cdot}{x} (t) = [\begin{array}{l} 0 & - 1 \\ 0 & - 0.1 \end{array}] x (t) + [\begin{array}{l} 0 \\ 0.1 \end{array}] u (t)$

通过网络控制上面的直流电机, 系统的控制器设计为:

$u (t) = [\begin{array}{l} - 3.75 & - 11.75 \end{array}] x (t)$

考虑到网络中存在的网络延时, 上述系统可以建模为一个时滞系统:

$\begin{array}{l} \overset{\cdot}{x} (t) = [\begin{array}{l} 0 & - 1 \\ 0 & - 0.1 \end{array}] x (t) + \\ {[0 0.1]}^{T} [\begin{array}{l} - 3.75 & - 11.5 \end{array}] x (t - d (t)) \end{array}$

假设网络延时有界, 假设网络延时下界 $h_{1} = 0.1,$ 表4对比了利用本文提出方法得到的最大网络延时上界以及文献[11, 12, 14]中的结果。从表4可以看出, 本文提出的方法与文献[11, 12, 14]相比具有更小的保守性。

表4 不同h₁得到的最大网络延时上界 Table 4 MUBNDs for different h₁

方法	$h_{1} = 0.1$	$h_{1} = 0.5$	$h_{1} = 1$
文献[11]	1.0377	1.0598	1.0853
文献[12]	1.0684	1.0768	1.0916
文献[14]	1.0640	1.0749	1.0943
定理1	1.0913	1.0981	1.1032

表4 不同h₁得到的最大网络延时上界 Table 4 MUBNDs for different h₁

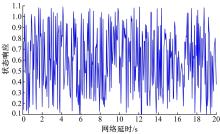
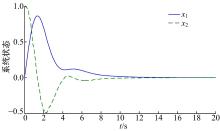
假设系统的初始状态为 $x (0) = {[0 1]}^{T},$ 网络延时满足 $0.1 < d (t) < 1.1,$ 如图1所示, 系统的状态响应曲线如图2所示。从图2可知, 系统渐近稳定, 从而证明了本文所提出方法的有效性。

	Figure Option View Download New Window
	图1 网络延时Fig.1 Network delay

	Figure Option View Download New Window
	图2 系统状态响应曲线Fig.2 System state response curve

3 结束语

研究了具有区间时变时滞的线性系统的稳定性问题。通过构造了一个新的增广Lyapunov泛函, 并利用最新提出的基于自由矩阵的积分不等式估计Lyapunov泛函的导数, 得到了一些保守性更小的稳定性条件。最后, 通过2个仿真示例验证了所提出方法有效。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Sun J, Liu G P, Chen J, et al. Networked predictive control for Hammerstein systems[J]. Asian Journal of Control, 2011, 13: 265-272. [本文引用:1]
[2]	Sun J, Chen J. Networked predictive control for systems with unknown or partially known delay[J]. IET Control Theory Appl, 2014, 8(18): 2282-2288. [本文引用:1]
[3]	李学军, 陈虹, 于树友. 基于时滞系统的无偏H_∞滤波[J]. 吉林大学学报: 工学版, 2009, 39(2): 473-479. Li Xue-jun, Chen Hong, Yu Shu-you. Unbiased H_∞filtering for time delay system[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(2): 473-479. [本文引用:1]
[4]	Fridman E, Shaked U. Delay-dependent stability and H_∞ control: constant and time-varying delays[J]. International Journal of Control, 2003, 76: 48-60. [本文引用:1]
[5]	Fridman E, Shaked U. An improved stabilization method for linear systems with time-delay[J]. IEEE Transactions on Automatic Control, 2002, 47: 1931-1937. [本文引用:1]
[6]	He Y, Wang Q G, Lin C, et al. Augmented Lyapunov functional and delay-dependent stability criteria for neutral systems[J]. International Journal of Robust and Nonlinear Control, 2005, 15: 923-933. [本文引用:1]
[7]	He Y, Wang Q G, Xie L, et al. Delay-range-dependent stability for systems with time-varying delay[J]. Automatica, 2007, 43: 371-376. [本文引用:1]
[8]	He Y, Wang Q G, Xie L, et al. Further improvement of free-weighting matrices technique for systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2007, 52: 293-299. [本文引用:1]
[9]	He Y, Wu M, She J H, et al. Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays[J]. Systems & Control Letters, 2004, 51: 57-65. [本文引用:1]
[10]	He Y, Wu M, She J H, et al. New delay-dependent stability criteria for robust stability of time-varying delay systems[J]. Automatica, 2004, 40: 1435-1439. [本文引用:1]
[11]	Sun J, Liu G P, Chen J, et al. Improved delay-range-dependent stability criteria for linear systems with time-varying delays[J]. Automatica, 2010, 46: 466-470. [本文引用:1]
[12]	Sun J, Han Q L, Chen J, et al. Less conservative stability criteria for linear systems with interval time-varying delays[J]. International Journal of Robust and Nonlinear Control, 2015, 25: 475-485. [本文引用:1]
[13]	Gu K. Integral inequality in the stability problem of time-delay systems[C]∥Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 2000, 3: 2805-2810. [本文引用:2]
[14]	Seuret A, Gouaisbaut F. Wirtinger-based integral inequality: application to time-delay systems[J]. Automatica, 2013, 49: 2860-2866. [本文引用:1]
[15]	Park P, Ko J W. Stability and robust stability for systems with a time-varying delay[J]. Automatica, 2007, 43: 1855-1858. [本文引用:1]
[16]	Park P, Ko J W, Jeong C. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica, 2011, 47: 235-238. [本文引用:1]
[17]	Gu K, Han Q L, Luo A C J, et al. Discretized lyapunov functional for systems with distributed delay and piecewise constant coefficients[J]. International Journal of Control, 2001, 74: 737-744. [本文引用:1]
[18]	Gouaisbaut F, Peaucelle D. Delay-dependent robust stability of time delay systems[C]∥Proceedings of IFAC Symposium on Robust Control Design, Toulouse, France, 2006, 5: 453-458. [本文引用:1]
[19]	Han Q L. New stability criteria for linear systems with interval time-varying delay[J]. Automatica, 2008, 44: 2680-2685. [本文引用:1]
[20]	Hui Jun-jun, Zhang He-xin, Kong Xiang-yu, et al. On improved delay-dependent robust stability criteria for uncertain systems with interval time-varying delay[J]. International Journal of Automation and Computing, 2015, 12(1): 102-108. [本文引用:1]
[21]	Fridman E. Tutorial on Lyapunov-based methods for time-delay systems[J]. European Journal of Control, 2014, 20(6): 271-283. [本文引用:1]
[22]	Zeng H B, He Y, Wu M, et al. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2015, 60(10): 2768-2772. [本文引用:2]
[23]	Sun J, Chen J. A survey on Lyapunov-based methods for stability of linear time-delay systems[J]. Frontiers of Computer Science, 2017, 11(4): 555-567. [本文引用:1]
[24]	Liu K, Fridman E, Johansson K H, et al. Generalized Jensen inequalities with application to stability analysis of systems with distributed delays over infinite time-horizons[J]. Automatica, 2016, 69: 222-231. [本文引用:1]
[25]	Kim J H. Further improvement of Jensen inequality and application to stability of time-delayed systems[J]. Automatica, 2016, 64: 121-125. [本文引用:1]

2011

0.0

... 0 引言时滞现象存在于许多实际系统中,例如化工控制过程,网络化控制系统^[1,2] ...

2014

0.0

... 0 引言时滞现象存在于许多实际系统中,例如化工控制过程,网络化控制系统^[1,2] ...

2009

0.0

... 时滞是引起系统不稳定和使系统性能恶化的主要原因之一^[3] ...

2003

0.0

2002

0.0

2005

0.0