引用本文
董飒, 刘大有, 欧阳若川, 朱允刚, 李丽娜. 引入二阶马尔可夫假设的逻辑回归异质性网络分类方法[J].吉林大学学报（工学版）, 2018,48(5): 1571-1577
DONG Sa, LIU Da-you, OUYANG Ruo-chuan, ZHU Yun-gang, LI Li-na. Logistic regression classification in networked data with heterophily based on second-order Markov assumption[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1571-1577  
Doi:10.13229/j.cnki.jdxbgxb20170717
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有 吉林大学学报编辑部
引入二阶马尔可夫假设的逻辑回归异质性网络分类方法
董飒1,2, 刘大有1,2, 欧阳若川3, 朱允刚1,2, 李丽娜1,2
1.吉林大学 计算机科学与技术学院,长春 130012
2.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012
3.吉林大学 大数据和网络管理中心,长春 130012
通信作者:刘杰(1973-),女,副教授.研究方向:数据挖掘,模式识别.E-mail:liu_jie@jlu.edu.cn

作者简介:董飒(1985-),女,工程师,博士研究生.研究方向:人工智能,数据挖掘.E-mail:dongsa7701@163.com

基金:国家自然科学基金项目 (61502198, 61572226, 61472161, 61373053);吉林省科技发展计划项目 (20150520066JH);应用光学国家重点实验室开放基金项目
摘要

针对异质性网络的分类问题提出了一种引入二阶马尔可夫假设链接的逻辑回归分类方法。该方法采用二阶马尔可夫链接,扩展结点邻居的邻居之链接特征(类分布)用于构造结构化的逻辑回归模型,并与基于一阶马尔可夫假设的逻辑回归模型相结合,利用松弛标注的协作推理方法逐步更新类分布至最终分类结果。对比实验结果表明,本文方法在异质性网络分类上分类精度较佳。

关键词: 人工智能; 异质性网络分类; 结构化逻辑回归模型; 网络数据
中图分类号:TP301 文献标志码:A 文章编号:1671-5497(2018)05-1571-07
Logistic regression classification in networked data with heterophily based on second-order Markov assumption
DONG Sa1,2, LIU Da-you1,2,, OUYANG Ruo-chuan3, ZHU Yun-gang1,2, LI Li-na1,2
1.College of Computer Science and Technology, Jilin University, Changchun 130012, China
2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun 130012, China
3.Big Data and Network Management Center, Jilin University, Changchun 130012, China
Abstract

A logistic regression classifier based on second-order Markov assumption is proposed for heterophilous network. The algorithm employs the second-order Markov links, extends neighbors' link distributions of node neighbors in order to construct structured logistic regression model. At the same time it combines the first-order Markov logistic regression model to update the class distributions progressively using relaxation labeling collective inference method. Comparison of experiment results shows that the enhanced algorithm performs better on the heterophilious network.

Keyword: artificial intelligence; heterophilous network classification; structured logistic regression model; networked data
0 引 言

大多数传统的分类方法假设数据实例是独立的并且根据数据实例的属性值进行分类, 为实例分配标签。在结构更加丰富的网络数据中, 数据往往不是独立且均匀分布的, 实例间的关系可以用来分类。网络数据分类比传统文本分类更加复杂。由于用于表达关系的链接的存在, 网络中的潜在关系需要适当处理, 利用这些信息可以提高学习模型的预测精确度。网络数据是指能被描述成网络的一组数据, 其中数据实例由结点表示, 它们之间的关系由边或链接表示。例如, 网页和超文本、社会网络、书目引用数据和流行病数据等。对网络数据结点进行抽样得到训练集, 分类器根据训练集结点的标签以及它们之间的链接对每个标签进行学习建模, 最终模型为测试集结点找到最佳匹配标签的过程就是网络数据分类。网络数据的关系分类方法多数是基于同质性假设的。同质性现象普遍存在于许多现实网络中。所谓同质性是指具有相似特征的结点趋向于彼此连接。相反即为异质性, 也可认为同质度较低。异质性是指互相连接的结点有很大比例不具有相同的类别。事实表明分类方法的有效性依赖于数据集和所使用的分类器。同质性假设是许多网络数据分类方法的前提假设。这些方法根据未标记结点的一阶(直接)邻居的类别对其进行分类。针对同质度高的网络这些方法可以得到合理的分类结果。然而对于异质性网络这些方法并不适用。

网络数据是相较独立且均匀分布的数据实例拥有更复杂结构的数据类型。对网络数据进行分类是主要的学习任务之一[1, 2, 3]。由Macskassy等[4]提出的加权投票关系近邻分类器WVRN是一种简单的基于同质性假设估计类分布概率的方法, 该方法假设未标记结点有很大的可能性与直接邻居结点集中出现次数最多的标签相同。Perlich等[5, 6]提出的类分布关系近邻分类器CDRN由未标记结点的类别向量和参考向量间的相似度分类结点。Lu等[7]提出了基于链接的分类器NLB, 使用结点的属性和链接分布分别构建逻辑回归模型, 结合两个模型的分类结果以最大后验概率分类结点。Chakrabarti等[8]将贝叶斯方法应用于网络数据得到网络贝叶斯方法NBC。随机游走方法MRW[9]在图上应用随机游走计算未标记结点类别。Mackassy等[10]通过实验表明相较于与迭代和吉布斯抽样的协作推理方法结合, WVRN和CDRN方法与松弛标注的协作推理方法联合使用能够大大提高数据分类的准确性, 可作为网络分类方法的基准方法。上述方法根据每个结点的一阶(直接)邻居结点的标签分类未标记结点, 事实上它们均是基于同质性假设[11]的方法, 针对同质性网络可得到合理的分类结果, 但对于异质性网络分类性能则明显下降。根据同质性的定义, 通过边相连接的不同结点具有很大的可能性拥有相同的类别, 但是对于大部分相连的结点具有不同类别的异质性网络, 上述方法得到的结果很不合理。鉴于此, Wang等[12]提出了基于概率的矩阵运算方法CPD对异质性网络进行分类。该方法结合迭代的协作推理方法将利用邻接矩阵计算得到的来自未标记结点邻居的影响在网络间进行传递。董飒等[13]改进了CDRN提出了基于类传播分布的关系近邻异质性网络分类方法PCDRN。该方法通过计算传播类别向量和传播参考向量, 比较两者的相似度并结合松弛标注的协作推理方法进行分类。Gupta等[14]提出了基于HeteClass框架的元路径直推式分类。该框架研究给定网络的模式并结合领域专家知识生成元路径集, 从而构建同质性信息网络。实验表明, 这几种方法对异质性网络展现了较好的分类性能。此外, 网络数据的关系分类方法与协作推理相结合处理稀疏标记的网络分类问题具有很好的效果[15, 16]。协作推理方法是基于马尔可夫假设的一组方法, 相连结点的类分布相互影响, 故可以同时被推理。典型的协作推理方法有迭代分类[7]、吉布斯抽样[17, 18]和松弛标注[8]方法等。

针对异质性网络的特殊性和重要性, 本文对基于链接的分类方法(NLB)进行改进, 使其适用于异质性网络数据的分类。本文方法引入了二阶马尔可夫假设, 将结点的二阶邻居的链接特征向量用于结构逻辑回归模型的训练和预测。在训练过程中分别基于已标记结点的一阶邻居和二阶邻居的链接特征向量训练出两个正则化逻辑回归模型。预测时同样分别用未标记结点的一阶和二阶邻居的链接特征向量进行预测, 结合预测结果后选取具有最大后验概率的类别进行分类。应用松弛标注的协作推理方法将一阶和二阶邻居类别对未标记结点的影响在网络中进行传递直至收敛或至稳定状态。将本文方法与其他5种方法在6个现实网络数据集上进行比较, 实验结果表明, 本文方法提高了异质性网络分类精度。

1 异质性网络分类模型

网络中不同结点之间存在一定的关系, 这种关系可能会直接影响网络数据分类。一个结点的标签也会对另一个结点造成影响。异质性现象也存在于许多现实网络中。使用直接邻居分类未标记结点的同质性方法往往分类性能不佳, 因为基于一阶马尔可夫假设的方法所考虑的一层邻居结点能反映的分类信息有限。本文将分类时关注的范围扩展到两层邻居, 结合两层邻居显然比一阶邻居结点包含了更多的语义信息。实验表明[8, 10], 邻居结点的标签不是内部属性决定了未标记结点的类别, 单纯使用邻居结点的属性甚至会降低分类精度, 许多实验数据表明网络结构本身已经包含了大量对实体分类有用的信息, 这也是对许多复杂网络数据问题代价较低的近似。与NLB不同, 在本文的研究中, 结点自身的属性被忽略, 分类过程只参考标签与链接信息[10]。针对同质性方法在异质性网络中分类性能不佳的情况, 并且避免引入过多噪声, 本文将二阶马尔可夫假设应用于基于链接的分类器NLB, 使其适用于异质性网络。

假定网络G中包含n个结点v1, v2, …, vn; xi表示结点vi(1≤ i≤ n)的类别取值, 也称标签, 其中xi∈ {c1, c2, …, cm}, m为类别个数。向量 {P(xi=ck)}k=1m为结点vi的类分布, 可以代表vi的类别, 其中 ∑k=1mP(xi=ck)=1。若结点的标签已知, 则类分布对应已知标签位置为1, 其余位置为0的向量。若结点vi与vj相连, wij表示结点间的权值, 本文考虑无向边, 则有wij=wji。令Ni表示结点vi的一阶邻居结点集。

逻辑回归在统计分析领域有着广泛的应用, 目前逻辑回归在网络数据分类方面也受到了相当的关注。传统的NLB分类器在同质性假设的基础上应用一阶马尔可夫假设将结点直接邻居的类分布(链接特征向量或链接分布)作为解释变量构建逻辑回归模型。而且NLB只能处理二类分类问题, 为了处理多类分类问题并能在异质性网络中取得较好的分类性能, 本文使用NLB的带有岭估计的逻辑回归模型的多类实现形式[10], 在本文中通过给定由结点vi的邻居结点计算得到的链接特征向量 LD(vi)作为输入向量(解释变量或预测变量), 计算未标记结点vi的类分布(依赖变量) {P(xi=ck|LD(vi))}k=1m, 其中LD(vi)包括结点vi的一阶邻居结点链接特征向量LD1(vi)和二阶邻居结点链接特征向量LD2(vi),本文定义如下:

LD1(vi)k=∑vj∈Niwij·P(xj=ck|Nj)(1)LD2(vi)k=∑vj∈Ni, vl∈Njwjl·P(xl=ck|Nl)(2)

逻辑回归通过逻辑函数 g(t)=ln(t/(1-t))对多元线性回归 g(P(xi=ck|LD(vi)))=ωTkLD(vi)进行逻辑变换从而确保任意两个类别之间的分界面为线性分界面。将事件发生的概率看作预测变量集的线性函数, 计算公式如下:

lnP(xi=ck|LD(vi))1-∑k=1m-1P(xi=ck|LD(vi))=ωTkLD(vi)(3)

式中: ωk为回归系数, ωkT=[ω0k, ω1k, ω2k, …, ωmk]。

已知有m个标签c1, c2, …, cm, 故cm为最后一个标签, 由式(3)可得标记结点vi为除cm外任意标签ck时的概率为:

P(xi=ck|LD(vi))=eωTkLD(vi)1+∑l=1m-1eωTlLD(vi)(4)

从而有结点vi标记为最后一个标签cm的概率:

P(xi=cm|LD(vi))=1-∑k=1m-1P(xi=ck|LD(vi))=11+∑l=1m-1eωTlLD(vi)(5)

已知对于n个训练结点的对数似然函数如下:

l(ω)=∑i=1nln[P(xi=ck|LD(vi))∑k=1m-1P(xi=ck)·P(xi=cm|LD(vi))P(xi=cm)](6)

在训练过程中 {P(xi=ck)}k=1m为已标记结点即训练结点的观测值。给定已标记结点构成的训练集 (LD(vi), {P(xi=ck)}k=1m), i⁼1, 2, …, n, 计算条件概率 P(xi=ck|LD(vi))的前提是在训练过程中为式(6)找到最优的ω , 相当于求使对数似然函数 l(ω)取极大值的ω, 计算公式如下:

ω^=arginfω∑i=1n[∑k=1m-1P(xi=ck)·lnP(xi=ck|LD(vi))+P(xi=cm)·lnP(xi=cm|LD(vi))]+λω2(7)

λω2是关于 ω的惩罚因子, 防止出现过拟合。采用拟牛顿方法[19]求最优的ω 。

本文方法中训练时 LD(vi)取一阶邻居结点链接特征向量LD1(vi)和二阶邻居结点特征向量LD2(vi分别进行建模, 由式(7)得到回归系数ω '和ω ″, 预测时分别由ω '和ω ″与式(4)(5)计算求得 {P(xi=ck|LD1(vi))}k=1m和 {P(xi=ck|LD2(vi))}k=1m, 最后结合两个类分布结果标记未标记结点为标签ck的概率为:

P^(xi=ck|LD(vi))=argmaxP(xi=ck|LD1(vi))·∑NiP(xi=ck|LD2(vi))(8)

对于相连接的结点, 更新一个结点的类分布会影响到与之相连接的邻居结点的类分布。故关系分类算法需结合协作推理方法对网络中结点进行同时推理。与NLB方法采用迭代的协作推理方法相区别, 本文采用改进的在子迭代中引入模拟退火的松弛标注协作推理方法[10, 13, 20], 每次迭代记录未标记结点的当前类分布(链接特征向量), 并在式(4)(5)中使用这些概率。算法收敛时将具有最大后验概率的标签指定给未标记结点:

P(xi|LD(vi))(t+1)=β(t+1)·P(xi|LD(vi))(t)+(1-β(t+1))·P(xi|LD(vi))(t+1)(9)

式中: β(t+1)=β(t)·α, β0=μ; μ为一个常数, 大于0且小于1, 在本文的研究中, 将其设置为1; t表示第几次迭代; 衰退常量α =0.99, 若α 设置太小, 其对相邻结点的影响也会减弱过快, 如果未标记结点较多时会降低性能。

2 实验与结果
2.1 实验设置与实验数据

为了测试本文方法(记为UNLB)的分类性能, 将其在现实网络上与其他3个同质性方法和2个异质性方法相比较。令r表示网络中所有结点中已标记结点的比例, 并令其从0.1取到0.9。网络中已标记结点根据每个r值进行10次类分层随机抽样得到训练集, 其余结点用作测试集, 而分类精度取10次运行的平均值, 即遵循标准的类分层10折交叉验证。

本文在6个标准网络数据集cora、imdb以及WebKB项目[7, 8, 10, 12, 13, 14]的4所大学的网页数据cornell, texas, washington和wisconsin上评估本文的分类方法。WebKB项目每个大学的网页都被分类为course, department, faculty, project, staff, student和other, 本文在实验中忽略other类别。网页间通过超链接建立关系。cora由机器学习相关论文构成, 被分类成7个主题, 由引用关系相互关联。imdb分类电影票房的高低, 根据电影的制作公司判断彼此之间的关系, 表1是6个数据集的信息。

表1 6个网络数据集信息 Table 1 Information for six networked data sets

同质度[21]的概念被应用于本文的研究中, 在网络数据中同质度是指结点直接邻居中与其标签相同的结点的占比, 计算公式如下:

H=∑i=1n(Si/Ni)n(10)

式中:H为同质度; n为网络中结点个数; |Si|为与结点vi具有相同类别的一阶邻居结点数; |Ni|为结点vi的一阶邻居结点数。

根据式(10)对表1的网络数据集进行计算得到相应的同质度, 如表2所示。

表2 表1中网络的同质度 Table 2 Homophily degrees of networks in table 1

由表2可以看出, cora和imdb是同质性网络, WebKB的4个网络为异质性网络, 同质度较低。

2.2 实验结果

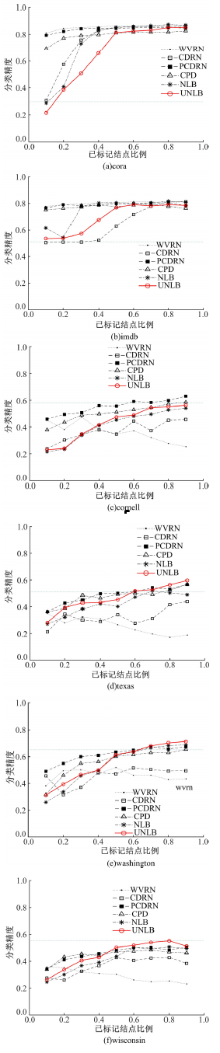
本文对比了不同的关系分类方法, 以此研究网络中多个不同分类模型对不同网络数据的分类性能。为了评估提出的UNLB方法的分类性能, 将其与5个关系分类器进行比较, 其中包含3个同质性方法WVRN、CDRN和NLB, 以及2个异质性方法CPD和PCDRN。与NLB采用迭代的协作推理方法不同, UNLB、WVRN、CDRN和PCDRN均与松弛标注的协作推理方法相结合。本文分类时采用只利用标签及链接信息的单变量分类方法, 并对孤立结点进行剪枝。6个关系分类方法的分类精度如图1所示。

图1 6个网络数据集的分类精度对比Fig.1 Comparison of classification accuracies on six networked data sets

从图1的实验结果可以看出, UNLB方法在WebKB的4个异质性数据集上相较于WVRN、CDRN和NLB方法展示了较好的性能, 特别是当r> 0.5时, 在数据集texas、 washington和wisconsin上分类精度优于异质性方法CPD。而在数据集texas和washington上, 当r> 0.6时UNLB分类精度优于PCDRN方法; 当r> 0.5时, UNLB方法在数据集wisconsin上分类精度优于PCDRN。虽然UNLB在cornell数据集上与CPD和PCDRN相比分类精度并无明显优势, 但是PCDRN的时间复杂度是O(mn3)[13], 而UNLB是广义线性回归方法, 时间复杂度只有O(mn2), 其中m为标签个数, n为训练结点数。CPD采用邻接矩阵的计算方式, 与UNLB每次只分类一个结点的方法相比空间复杂度较高。Mackassy等[4]指出WVRN和CDRN是网络分类的基准方法, 但由于它们均是基于同质性假设的, 在异质性网络数据集上分类效果不佳。而本文提出的UNLB方法引入了二阶马尔可夫假设, 打破了同质性假设方法的局限, 二层邻居的分类信息引入进来, 故改进后分类精度不仅优于NLB方法, 更大大优于WVRN和CDRN方法。当r> 0.5时, UNLB方法在cora与imdb数据集上与其他5个方法的分类精度不相上下, 这说明当已标记结点超过50%时UNLB方法在同质性网络数据集上同样具有优势。

3 结束语

对于大部分相连接的结点类别不同的异质性网络数据, 沿用传统的分类方法, 并不能取得较好的效果。本文将二阶马尔可夫假设引入到基于链接的分类方法中, 使用结点的一阶和二阶链接特征向量对多类结构化逻辑回归模型进行建模, 结合松弛标注的协作推理方法进行分类。虽然相较NLB方法增加了时间复杂度, 但实验结果表明此方法对异质性网络数据分类性能较佳。

The authors have declared that no competing interests exist.

参考文献
[1] Mcdowell L K, Aha D W. Leveraging neighbor attributes for classification in sparsely labeled networks[J]. ACM Transactions on Knowledge Discovery from Data, 2016, 11(1): 1-37. [本文引用:1]
[2] Li M, Pan S R, Zhang Y, et al. Classifying networked text data with positive and unlabeled examples[J]. Pattern Recognition Letters, 2016, 77: 1-7. [本文引用:1]
[3] King J R, Mcdowell L K. Correcting relational bias to improve classification in sparsely-labeled Networks[C]∥Proceedings of 3rd IEEE/ACM International Conference on Data Science and Advanced Analytics, Montral, Canada, 2016: 31-40. [本文引用:1]
[4] Macskassy S A, Provost F. A simple relational classifie[C]∥Proceedings of the Multi-Relational Data Mining Workshop at the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, 2003: 24-27. [本文引用:2]
[5] Perlich C, Provost F. Distribution-based aggregation for relational leaning with identifier attributes[J]. Machine Learning, 2006, 62(1/2): 65-105. [本文引用:1]
[6] Perlich C, Provost F. Aggregation-based feature invention and relational concept classes[C]∥Proceedings of 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington DC, 2003: 167-176. [本文引用:1]
[7] Lu Q, Getoor L. Link-based classification[C]∥Proceedings of 12th International Conference on Machine Learning (ICML), Washington DC, 2003: 496-503. [本文引用:3]
[8] Chakrabarti S, Dom B, Indyk P. Enhanced hypertext categorization using hyperlinks[C]∥Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data, New York, USA, 1998: 307-319. [本文引用:4]
[9] Lin F, Cohen W W. Semi-supervised classification of network data using very few labels[C]∥Proceedings of the International Conference on Advances in Social Network Analysis and Mining, IEEE Computer Society, Washington, DC, USA, 2010: 192-199. [本文引用:1]
[10] Macskassy S A, Provost F. Classification in networked data: a toolkit and a univariate case study[J]. Journal of Machine Learning Research, 2007, 8(3): 935-983. [本文引用:6]
[11] McPherson M, Smith-Lovin L, Cook J M. Birds of a feather: homophily in social networks[J]. Annual Review of Sociology, 2001, 27: 415-444. [本文引用:1]
[12] Wang Zhen-wen, Yin Feng-jing, Tan Wen-tang, et al. Classification in networked data with heterophily[J]. The Scientific World Journal, 2013, 2013(2): 236769. [本文引用:2]
[13] 董飒, 刘大有, 李丽娜, 等. 基于类传播分布的关系近邻异质性网络分类方法[J]. 吉林大学学报: 工学版, 2016, 46(2): 522-527.
Dong Sa, Liu Da-you, Li Li-na, et al. Relational neighbor algorithm based on class propagation distributions for classification in networked data with heterophily[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(2): 522-527. [本文引用:4]
[14] Gupta M, Kumar P, Bhasker B. HeteClass: a meta-path based framework for transductive classification of objects in heterogeneous information networks[J]. Expert Systems with Applications, 2017, 68: 106-122. [本文引用:2]
[15] 李丽娜. 基于链接的网络分类和链接预测新方法研究[D]. 长春: 吉林大学计算机科学与技术学院, 2012.
Li Li-na. Research on classification and link prediction of network data based on links[D]. Changchun: College of Computer Science and Technology, Jilin University, 2012. [本文引用:1]
[16] 林金花, 王延杰. 三维语义场景复原网络[J]. 光学精密工程, 2018, 26(5): 1231-1241.
Lin Jin-hua, Wang Yan-jie. Three-dimentional reconstruction of semantic scene based on RGB-D map[J]. Optics and Precision Engineering, 2018, 26(5): 1231-1241. [本文引用:1]
[17] Geman S, Geman D. Stochastic relaxation, Gibbs distributions and Bayesian restoration of images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984(6): 721-741. [本文引用:1]
[18] Zhang T, Oles F J. Text categorization based on regularized linear classification methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 4(1): 5-13. [本文引用:1]
[19] Le Cessie S, van Houwelingen J C. Ridge estimators in logistic regression[J]. Applied Statistics, 1992, 41(1): 191-201. [本文引用:1]
[20] 高瞻宇, 顾营迎, 刘宇航, 等. 采用简化Brown模型及改进BFGS法的相机自标定[J]. 光学精密工程, 2017, 25(9): 2532-2540.
Gao Zhan-yu, Gu Ying-ying, Liu Yu-hang, et al. Self-calibration based on simplified brown non-linear camera model and modified BFGS algorithm[J]. Optics and Precision Engineering, 2017, 25(9): 2532-2540. [本文引用:1]
[21] Sen P, Namata G M, Bilgic M, et al. Collective classication in network data[J]. AI Magazine, 2008, 29(3): 93-106. [本文引用:1]