基于优化<em> k</em>-mer频率的宏基因组聚类方法

引用本文

刘富, 兰旭腾, 侯涛, 康冰, 刘云, 林彩霞. 基于优化 k-mer频率的宏基因组聚类方法 [J].吉林大学学报（工学版）, 2018,48(5): 1593-1599
LIU Fu, LAN Xu-teng, HOU Tao, KANG Bing, LIU Yun, LIN Cai-xia. Metagenomic clustering method based on k-mer frequency optimization [J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1593-1599 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170668
Permissions

基于优化 k-mer频率的宏基因组聚类方法

刘富^1,², 兰旭腾^1,², 侯涛², 康冰², 刘云², 林彩霞³

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.吉林大学通信工程学院,长春 130022

3.海南大学信息科学与技术学院, 海口 570228

作者简介:刘富(1968-),男,教授,博士生导师.研究方向:计算机视觉及模式识别.E-mail:liufu@jlu.edu.cn

基金:国家自然科学基金项目(61503151);吉林省青年科研基金项目(20160520100JH);吉林省省级产业创新专项资金项目(2017C032-4,2017C045-4);海南自然科学基金面上项目(0112631040)

摘要

k-mer频率是进行宏基因组分类时的一种重要的数字特征,然而该特征的维数随参数 k的增加呈指数增长,利用该特征进行宏基因组分类易陷入“维数灾难”。为解决此问题,本文提出了一种基于优化 k-mer频率的宏基因组DNA序列聚类方法。首先,提取DNA序列的 k-mer频率特征;其次,使用非负矩阵分解算法对DNA序列的 k-mer频率特征进行优化;最后,利用模糊C均值算法进行聚类。将本文方法在包含有不同物种个数的模拟宏基因组数据上运行的结果表明,其能有效地克服现有宏基因组数据分类方法计算量大的缺点,且分类性能优于同类算法。

关键词: 计算机应用; 模式识别与智能系统; k-mer; 非负矩阵分解; 模糊C均值; 宏基因组

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2018)05-1593-07

Metagenomic clustering method based on k-mer frequency optimization

LIU Fu^1,², LAN Xu-teng^1,², HOU Tao², KANG Bing², LIU Yun², LIN Cai-xia³

1.State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022,China

2.College of Communication Engineering, Jilin University, Changchun 130022, China

3.College of Information Science &Technology, Hainan University, Haikou 570228, China;

Abstract

DNA sequence classification is a very important step in metagenomic study, and k-mer frequency is a commonly used feature for DNA sequence classification. The dimension of k-mer grows exponentially with k, easily leading to the “dimension disaster”. To solve this problem, this paper proposes a k-mer optimization based metagenomic DNA sequence classification method. First, the k-mer frequency is extracted for each DNA sequence. Second, the k-mer frequency is optimized based on Non-negative Matrix Factorization (NMF) algorithm. Finally, the fuzzy C-means clustering algorithm is used for DNA sequence clustering. Experimental results on metagenomic datasets containing different species show that the proposed method can effectively overcome the shortcoming of traditional classification method, and the classification performance is better than that of several similar algorithms.

Keyword: computer application; pattern recognition and intelligent systems; k-mer; non-negative matrix factorization(NMF); fuzzy C-means method; metagenome

文章图片

0 引言

宏基因组是以特定环境中的所有微生物群落作为研究对象, 无需将群落分离培养, 而是直接提取环境样本中所有DNA进行测序, 进而研究环境微生物的群落结构、系统进化、物种分类、基因功能及代谢网络等^[1]。鉴于宏基因组研究的上述特性, 该方法目前广泛应用于微生物研究领域。其数据特点是大量不同物种的DNA序列混杂, 因此, 将大量DNA序列按照其物种属性进行分类是宏基因组分析的重要一步, 人们往往要提取每个DNA片段的数字特征再进行分类, 如何从DNA序列中提取优质的数字特征, 是从理论上提高宏基因组内细菌DNA片段种群分类平台精度及速度的先行条件。

Burge等^[2]发现, 对于某物种, 由A、T、G、C四种碱基组成的所有短序列片段的频率分布在全基因组中具有稳定性, 并在进一步的实验中证明这种特性可以代表生物的本质属性— — 可作为标记生物的物种标签, 称为k-mer频率。在进行宏基因组分类时, 通常提取DNA短序列的k-mer频率来作为物种的数字特征向量, 并在一个个特征向量之间寻找差异来衡量物种差别, 从而在计算水平上进行宏基因组序列样本的分类^[3]。从一个固定长度的DNA片段中提取的k-mer频率的维数是4^k, k取值越高, k-mer频率特征表征物种的能力就越强。现有的宏基因组分类平台, 如:NBC取k=15^[4]; PhyloPythia平台及PhyloPythiaS, 前者取k=7, 后者做频率组合, 分别取k=4, 5, 6^[5]。以上取值意味着, 对于一段DNA短序列要取得比较理想的识别精度, 需要提取一个近万维的向量作为物种标签。然而, 特征向量维数过大, 就会在用已知细菌DNA序列建立数据库的训练阶段以及对未知细菌DNA序列的分类阶段产生巨大的计算量。

为解决k-mer频率在分类过程中效率低的问题, Meinicke等^[6]提出GRS(Genome ReSequencing)方法, 对大米宏基因组及韩国人类宏基因组的k-mer特征频率属性进行优化; 刘富等^[7]提出用粗糙集的属性优化理论对k-mer特征频率进行优化; Koslicki等^[8]提出用压缩感知理论对k-mer特征频率进行属性优化。这些特征优化方法节约了内存存储空间, 缩短了计算时间, 然而对分类性能的提高影响不大。

非负矩阵分解(Nonnegative matrix factorization, NMF)是在矩阵中所有元素均为非负数约束条件之下的矩阵分解算法, 为大规模数据处理的研究提供了一个新思路^[9]。从计算的传统角度看, 矩阵分解结果中存在负值是合理的, 但负值元素在某些实际问题中是没有意义的^[10]。正如k-mer频率值不存在负值, 若采用传统的因子分析方法(如主成分分析), 结果中的负数就没有物理意义, 无法从物理角度进行解读; 反之, 采用非负矩阵分解方法就可以避免这一点^[11]。

本文引入非负矩阵分解算法对宏基因组的k-mer频率进行优化, 并在此基础上对宏基因组内DNA片段进行分类, 以提升分类效率。本文首先提取DNA序列的k-mer频率特征向量, 再对特征向量进行有效的优化, 从原始特征向量中去除冗余信息, 筛选出一个最优特征子集作成为物种标签, 最后再利用聚类算法^{[12, 13, 14, 15, 16]}进行分类。这样做一方面能减少特征个数, 提高模型精确度, 减少运行时间; 另一方面, 选取出每个细菌群落的最优特征便于研究这些细菌之间最本质的进化关系。为验证本文所提方法, 分别对5类、10类和20类微生物序列样本进行测试, 结果表明, 该分类策略显著提升了分类效果, 大幅节约了内存存储空间, 并且缩短了计算时间。

1 方法介绍

1.1 k-mer频率提取

记 $N$ 为长度为 $L$ 的序列, 则 $N = N_{1}, N_{2}, \dots, N_{L},$ 其中N_i∈ {A, T, G, C}。k-mer是指序列中长度为k的子序列, 对长度为 $L$ 的序列, k-mer频率的计算方法是:用宽度为 $k$ 的滑框, 从第1个到第 $L - k + 1$ 位置, 每次将滑框移动一个碱基位, 直到遍历整个基因组短序列, 导出的特征向量为:

$F = (f_{1}, f_{2}, \dots, f_{4^{k}}) (1)$

式中: $f_{i}$ 为相应特征(式(1)的各分量)的原始累计频数, 且 $M = 4^{k}$ 为所有可能的k-mer特征频率的总数, 因而, 向量 $F$ 可用其自身的长度 $L - k + 1$ 进行归一化, 用以消除每条基因组短序列因长度互不相同而产生的“ 负面” 影响。由于DNA具有双链结构, 每一个DNA序列可由双链中的任意一链测序得来。因此, 某一k长度子序列的出现频率便可与它反向互补序列的出现频率合二为一, 经上述操作, 能将特征向量 $F$ 的维数减少一半左右^[17]。考虑到回文序列与其反向互补序列相同, 当k为奇数时, 特征向量 $F$ 的维数可以约简至4^k/2, 当k为偶数时, 特征向量 $F$ 的维数可以约简至(4^k+4^k^/2)/2。

Alsop等^[18]证明, 当k=7时, k-mer频率可以较好地兼顾稳定性和计算效率。所以, 本文对每个序列提取7-mer频率作为特征向量, 所取的原始k-mer频率的维数为8192维。

1.2 利用NMF算法进行特征优化

测试样本矩阵是一个稀疏矩阵, 含有大量的“ 0元素” 。按照传统的方法, 提取k-mer频率后, 对样本矩阵进行聚类, 这种情况下计算大, 存储空间上也有巨大浪费, 并且因为冗余项过多, 对分类效果影响十分显著。最明显的表现为:聚类数目远小于实际分类数目; 而对矩阵进行优化处理, 去除冗余信息, 提升聚类准确度, 节约存储空间。

将所有片段提取k-mer频率, 组合成k-mer频率特征矩阵 $V \in R_{n \times m}^{+},$ 随后根据NMF算法寻找非负矩阵 $W \in R_{n \times r}^{+}$ 和非负矩阵 $H \in R_{r \times m}^{+},$ 使得 $V \approx WH 。$ 即:k-mer频率特征矩阵 $V$ 中列向量是对矩阵 $W$ 中所有列向量的加权和, 而权重系数便为矩阵 $H$ 中对应的列向量元素, 这里一般称 $W$ 为基矩阵, $H$ 为系数矩阵。一般情况下, $r$ 值的选择要小于 $n,$ 即满足 $(m + n) r < mn,$ 这时用系数矩阵 $H$ 代替k-mer频率特征矩阵 $V,$ 就可以实现对k-mer频率特征矩阵的优化, 得到数据特征的优化矩阵。NMF算法中目标函数有很多, 主要为以下两种:平方距离和KL散度。其中, 针对平方距离得到的乘法更新法则为:

$\begin{array}{l} W_{i, k} = W_{i, k} \frac{{(V H^{T})}_{i, k}}{{(WH H^{T})}_{i, k}} (2) \\ H_{k, j} = H_{k, j} \frac{{(W^{T} V)}_{k, j}}{{(W^{T} WH)}_{k, j}} (3) \end{array}$

针对KL散度得到的乘法更新法则为:

$\begin{array}{l} W_{i, k} = W_{i, k} \frac{\sum_{u} H_{k, u} V_{i, u} / {(WH)}_{i, u}}{\sum_{v} H_{k, v}} (4) \\ H_{k, j} = H_{k, j} \frac{\sum_{u} W_{u, k} V_{u, j} / {(WH)}_{u, j}}{\sum_{v} W_{v, k}} (5) \end{array}$

利用上述乘法更新法则, 可以在计算过程中保证非负, 本文选取了针对平方距离得到的损失函数。

1.3 聚类

完成特征优化之后, 进行聚类分析验证, 本文采用模糊C均值(Fuzzy C-means, FCM)算法^{[19, 20]}对优化之后的数据进行聚类分析。

FCM算法的基本思想是:根据每个数据对C个聚类中心的隶属度对目标函数进行迭代最小化, 从而决定样本点的类属行达到分类的目的。目标函数定义如下:

$J (U, V) = \overset{c}{\sum_{i = 1}} \overset{n}{\sum_{k = 1}} (u_{ik})^{m} ‖ x_{k} - v_{i} ‖^{2} (6)$

且满足条件:

$\begin{array}{l} \overset{c}{\sum_{i = 1}} u_{ik} = 1, \\ 0 \leq u_{ik} \leq 1; k = 1, 2, \dots, n; i = 1, 2, \dots, c \end{array}$

式中: $X = {x_{1}, x_{2}, \dots, x_{n}}$ 为聚类样本集合; $n$ 为聚类空间的样本个数; $V = {v_{1}, v_{2}, \dots, v_{n}}$ 为c个聚类中心, c为聚类的类别数; $(x_{k} - v_{i})$ 为 $x_{k}$ 和 $v_{i}$ 之间的归一化距离; $U = [u_{ik}]$ 为 $c \times n$ 维矩阵; $u_{ik}$ 为第k个样本对i类的隶属度值。

FCM算法的实现步骤如下:

(1)用随机数生成法产生隶属度初始矩阵 $U (1)$ , 且 $U (1)$ 满足约束条件; 设定聚类数目c和模糊度加权指数m, 迭代截止误差 $ε > 0 。$

(2)计算聚类中心 $V 。$

$\begin{array}{l} v_{i} = \frac{\overset{n}{\sum_{k = 1}} {(u_{ik})}^{m} x_{k}}{\overset{n}{\sum_{k = 1}} {(u_{ik})}^{m}} (7) \\ i = 1, 2, \dots, c; k = 1, 2, \dots, n \end{array}$

(3)更新隶属度值u_ik。

$\begin{array}{l} u_{ik} = 1 / \overset{c}{\sum_{j = 1}} {(\frac{‖ x_{k} - v_{i} ‖}{‖ x_{k} - v_{j} ‖})}^{\frac{2}{m - 1}} (8) \\ i = 1, 2, \dots, c; k = 1, 2, \dots, n \end{array}$

(4)重复步骤(2)(3), 直到 $(U^{l} - U^{l - 1}) < ε (ε$ 为预定的误差值)停止计算。

利用FCM对前文优化矩阵进行聚类, 聚类完成后, 将聚类结果与真实结果进行对比。

2 实验结果

2.1 实验数据

本文从美国生物信息中心(NCBI, https:∥www.ncbi.nlm.nih.gov/)获得数据, 从该网站上下载了25个细菌全基因组序列, 并从中随机选出5类、10类、20类组成模拟宏基因组测试数据, 数据详细信息如表1~表3所示。依前文数据提取方法提取样本数据, 将每类细菌全基因组序列以500碱基为一组进行划分, 并将序列最后一组不足500碱基的冗余部分去除, 然后每隔9组取1组作为该类细菌的一个DNA片段样本, 以此类推, 5类模拟宏基因组数据共提取出7362个不重复DNA片段组成测试样本, 10类和20类模拟宏基因组数据分别由21 162和41 122段不重叠的DNA片段组成。

表1 5分类实验数据集 Table 1 5 classification experiment data sets

表2 10分类实验数据集 Table 2 10 classification experiment data sets

表3 20分类实验数据集 Table 3 20 classification experiment data sets

提取出模拟宏基因组数据后, 对样本数据提取k-mer频率, 生成特征值矩阵:5分类测试样本生成7362× 8192维矩阵, 10分类测试样本生成21 162× 8192维矩阵, 20分类测试样本生成41 122× 8192维矩阵。随后, 用NMF算法对特征值矩阵进行优化, 优化后的特征值数量为6, 这样5分类测试样本优化成7362× 6维矩阵, 10分类测试样本优化成21 162× 6维矩阵, 20分类测试样本优化成41 122× 6维矩阵。

2.2 评价指标

本文使用文献[21]的3个标准, 即准确率、召回率、F率来评价所提方法的聚类性能。设定 $X$ 为原始数据集, $C = {C_{1}, C_{2}, \dots, C_{k}}$ 为聚类结果, $k$ 为真实数据类数, $P = {P_{1}, P_{2}, \dots, P_{k'}}$ 为 $X$ 的一个原始划分, $k'$ 为聚类结果类数, 则计算公式如下:

(1)准确率

$PE = \frac{1}{k} \overset{k}{\sum_{i = 1}} \frac{ma x_{j = 1}^{k'} n_{ij}}{b_{i}} (9)$

(2)召回率

$RE = \frac{1}{k} \overset{k}{\sum_{i = 1}} \frac{ma x_{j = 1}^{k'} n_{ij}}{d_{argma x_{j = 1}^{k'}} n_{ij}} (10)$

(3)F率

$F = \frac{2 \times PE \times RE}{(PE + RE)} (11)$

式中: $n_{ij}$ 为 $C_{i}$ 和 $P_{j}$ 中的共存元素: $n_{ij} = |C_{i} ⋂ P_{j}|, b_{i}$ 为 $C_{i}$ 中元素中的数目, $d_{j}$ 为 $P_{j}$ 中元素的数目。

2.3 实验结果

2.3.1 分类性能对比

为了验证本文所提分类策略的性能, 将FCM方法与本文方法以及文献[15]中的宏基因组分类方法MetaCluster3.0进行了效果对比。

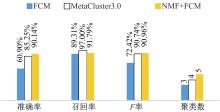
3种方法在5分类的模拟宏基因组数据上的分类结果如图1所示。本文所提的优化分类策略在5分类数据上的分类准确率为90.14%, 召回率为91.79%, F率为90.96%, 聚类数为5。而没有优化的FCM和MetaCluster3.0方法, 在5分类数据上的分类准确率分别为60.90%和85.25%, 召回率分别为89.31%和97%, F率分别为72.42%和90.74%, 聚类数分别为3和4。各项指标中, 本文方法准确率优于其他两种方法, 召回率上低于MetaCluster3.0方法, 优于FCM方法, F率优于其他两种方法, 在聚类数上, 全面优于其他两种方法。

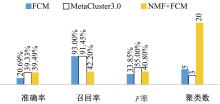
	Figure Option View Download New Window
	图1 三种方法5分类数据上的分类性能对比Fig.1 Comparative results of 3 methods on 5 datasets

3种方法在10分类的模拟宏基因组数据上的分类结果如图2所示。本文所提的优化分类策略在10分类数据上的分类准确率为65.98%, 召回率为65.74%, F率为65.86%, 聚类数为10。而没有优化的FCM和MetaCluster3.0方法, 在10分类数据上的分类准确率分别为29.31%和64.25%, 召回率分别为92.67%和94.90%, F率分别为44.53%和76.62%, 聚类数都是3。各项指标中, 本文方法准确率优于其他两种方法, 召回率上低于MetaCluster3.0和FCM方法, F率低于MetaCluster3.0方法, 高于FCM方法, 在聚类数上, 全面优于其他两种方法。

	Figure Option View Download New Window
	图2 三种方法10分类数据上的分类性能对比Fig.2 Comparative results of 3 methods on 10 datasets

3种方法在20分类的模拟宏基因组数据上的分类结果如图3所示。本文所提的优化分类策略在20分类数据上的分类准确率为39.49%, 召回率为42.2%, F率为40.8%, 聚类数为20。而没有优化的FCM和MetaCluster3.0方法, 在20分类数据上的分类准确率分别为20.69%和39.33%, 召回率分别为93%和91.45%, F率分别为33.85%和55%, 聚类数分别为5和3。各项指标中, 本文方法准确率优于其他两种方法, 召回率上低于其他两种方法, F率低于MetaCluster3.0方法, 高于FCM方法, 在聚类数上, 全面优于其他两种方法。

	Figure Option View Download New Window
	图3 三种方法20分类数据上的分类性能对比Fig.3 Comparative results of 3 methods on 20 datasets

综上, 本文分类策略在5分类、10分类及20分类上的准确率和聚类数都全面优于MetaCluster3.0和FCM方法。对于FCM和MetaCluster3.0方法, 聚类结果中召回率较高的原因是:FCM方法和MetaCluster3.0方法的聚类数目较低, 会使不同类别的样本都被划分到同一类别, 这样就会导致计算召回率时结果较高。

在F率上, 本文分类策略全面高于FCM方法, 在5分类时高于MetaCluster3.0方法, 10分类和20分类时低于该方法。这是因为FCM和MetaCluster3.0方法中召回率较高, 从而影响了F率的结果。

针对宏基因组分类方法性能, 要从多个评价标准综合评定, 以上图表表明本文方法各项指标效果提升明显, 特别是在准确率和聚类数上有着明显优势, 该方法的可行性很高。

2.3.2 优化前、后的数据占用空间及时间对比

优化前、后的数据占用空间及时间对比如表4所示。占用空间方面, 数据集在5分类、10分类和20分类数据上分别进行优化, 结果显示优化后的3类数据占用空间分别缩小了97.26%、96.99%和97.04%。运行时间上, 优化后的3类数据分别缩短了8.16%、31.94%和73.67%。总之, 本文提出的优化分类策略与同类分类方法相比, 在减少占用空间上效果明显, 优化后的数据占用空间很小, 同时运行时间大幅下降。

表4 数据集优化前、后对比及运行时间 Table 4 Result comparison of data sets before and after optimization ation and operation time

3 结束语

针对k-mer频率特征维数较高、数据占用空间较大以及分类性能偏低的问题, 本文提出了一种优化k-mer频率的宏基因组数据分类策略, 利用非负矩阵分解算法对k-mer特征进行优化。在包含有不同物种个数的宏基因组数据集上的聚类实验表明, 该策略有效地提高了准确率、F值和聚类数量, 最终提高了细菌微生物的DNA片段识别效率。本策略也存在一定的局限性, 一是随着样本数量的上升, 各项指标下降比较明显, 在面对实际样本的操作中, 需要进一步研究如何提升聚类效果:拟在接下来的试验中寻求对NMF算法的深入改进方法以及针对数据模式进行优化, 从这两点入手提升聚类效果; 二是在NMF算法中, 如何合理选择优化后的特征维数还需要进一步进行研究:拟在接下来的试验中, 对NMF算法中的基矩阵 $W$ 初始化着手, 通过实验得出最优特征维数。下一步的工作将围绕这两点进行。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Teeling H, Glöckner F O. Current opportunities and challenges in microbial metagenome analysis—a bioinformatic perspective[J]. Briefings in Bioinformatics, 2012, 13(6): 728-742. [本文引用:1]
[2]	Burge C B, Karlin S. Finding the genes in genomic DNA[J]. Current Opinion in Structural Biology, 1998, 8(3): 346-354. [本文引用:1]
[3]	Borodovskii M Y, Sprizhitskii Y A, Golovanov E I, et al. Statistical patterns in primary structures of functional regions in the E. coli genome. I. Oligonucleotide frequencies analysis[J]. Molecular Biology, 1986, 77(7): 3816-3820. [本文引用:1]
[4]	Rosen G L, Reichenberger E R, Rosenfeld A M. NBC: the Naïve Bayes Classification tool webserver for taxonomic classification of metagenomic reads[J]. Bioinformatics, 2011, 27(1): 127-129. [本文引用:1]
[5]	Gregor I, Dröge J, Schirmer M, et al. PhyloPythiaS+: a self-training method for the rapid reconstruction of low-ranking taxonomic bins from metagenomes[J]. Peer J, 2016, 4(10): e1603. [本文引用:1]
[6]	Meinicke P, Aßhauer K P, Lingner T. Mixture models for analysis of the taxonomic composition of metagenomes[J]. Bioinformatics, 2011, 27(12): 1618-1624. [本文引用:1]
[7]	刘富, 张潇, 侯涛, 等. 基于粗糙集的基因信号属性约简[J]. 吉林大学学报: 工学版, 2015, 45(2): 624-629. Liu Fu, Zhang Xiao, Hou Tao, et al. Attributes reduction of gene signal based on rough set[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(2): 624-629. [本文引用:1]
[8]	Koslicki D, Foucart S, Rosen G. Quikr: a method for rapid reconstruction of bacterial communities via compressive sensing[J]. Bioinformatics, 2013, 29(17): 2096-2102. [本文引用:1]
[9]	Jiang X, Weitz J S, Dushoff J. A non-negative matrix factorization framework for identifying modular patterns in metagenomic profile data[J]. Journal of Mathematical Biology, 2012, 64(4): 697-711. [本文引用:1]
[10]	Liang Z, Li Y, Zhao T. Projected gradient method for kernel discriminant nonnegative matrix factorization and the applications[J]. Signal Processing, 2010, 90(7): 2150-2163. [本文引用:1]
[11]	Lin C J. On the convergence of multiplicative update algorithms for nonnegative matrix factorization[J]. IEEE Transactions on Neural Networks, 2014, 18(6): 1589-1596. [本文引用:1]
[12]	李华, 杨帆, 杨华民, 等. 条纹颜色分离与聚类[J]. 光学精密工程, 2016, 24(5): 1206-1214. Li Hua, Yang Fan, Yang Hua-min, et al. Separating and clustering of structured light stripe colo[J]. Optics and Precision Engineering, 2016, 24(5): 1206-1214. [本文引用:1]
[13]	赵文昌, 李忠木. 融合改进人工蜂群和K均值聚类的图像分割[J]. 液晶与显示, 2017, 32(9): 726-735. Zhao Wen-chang, Li Zhong-mu. Image segmentation algorithm based on improved artificial bee colony and K-mean clustering[J]. Chinese Journal of Liquid Crystal and Displays, 2017, 32(9): 726-735. [本文引用:1]
[14]	郭少军, 娄树理, 刘峰. 应用颜色聚类图像块的多舰船显著性检测[J]. 光学精密工程, 2016, 24(7): 1807-1817. Guo Shao-jun, Lou Shu-li, Liu Feng. Multi-ship saliency detection via patch fusion by color clustering[J]. Optics and Precision Engineering, 2016, 24(7): 1807-1817. [本文引用:1]
[15]	王永, 万潇逸, 陶娅芝, 等. 基于K-medoids项目聚类的协同过滤推荐算法[J]. 重庆邮电大学学报: 自然科学版, 2017, 29(4): 521-526. Wang Yong, Wan Xiao-yi, Tao Ya-zhi, et al. Collaborative filtering recommendation algorithm based on K-medoids item clustering[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2017, 29(4): 521-526. [本文引用:2]
[16]	杨玉梅. 基于信息熵改进的 K-means 动态聚类算法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(2): 254-259. Yang Yu-mei. Improved K-means dynamic clustering algorithm based on information entropy[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2016, 28(2): 254-259. [本文引用:1]
[17]	Leung H C, Yiu S M, Yang B, et al. A robust and accurate binning algorithm for metagenomic sequences with arbitrary species abundance ratio[J]. Bioinformatics, 2011, 27(11): 1489-1495. [本文引用:1]
[18]	Alsop E B, Raymond J. Resolving prokaryotic taxonomy without rRNA: longer oligonucleotide word lengths improve genome and metagenome taxonomic classification[J]. Plos One, 2013, 8(7): e67337. [本文引用:1]
[19]	吴秋红, 吴谨, 朱磊, 等. 基于图论和FCM的图像分割算法[J]. 液晶与显示, 2016, 31(1): 112-116. Wu Qiu-hong, Wu Jin, Zhu Lei, et al. Image segmentation algorithm based on graph theory and FCM[J]. Chinese Journal of Liquid Crystal and Displays, 2016, 31(1): 112-116. [本文引用:1]
[20]	王民, 张鑫, 贠卫国, 等. 基于核模糊C-均值和EM混合聚类算法的遥感图像分割[J]. 液晶与显示, 2017, 32(12): 999-1005. Wang Min, Zhang Xin, Yun Wei-guo, et al. Remote sensing image segmentation based on KFCM and EM hybrid clustering algorithm[J]. Chinese Journal of Liquid Crystal and Displays, 2017, 32(12): 999-1005. [本文引用:1]
[21]	Liang J, Bai L, Dang C, et al. The K-means-type algorithms versus imbalanced data distributions[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(4): 728-745. [本文引用:1]

2012

0.0

... 0 引言宏基因组是以特定环境中的所有微生物群落作为研究对象,无需将群落分离培养,而是直接提取环境样本中所有DNA进行测序,进而研究环境微生物的群落结构、系统进化、物种分类、基因功能及代谢网络等^[1] ...

1998

0.0

... Burge等^[2]发现,对于某物种,由A、T、G、C四种碱基组成的所有短序列片段的频率分布在全基因组中具有稳定性,并在进一步的实验中证明这种特性可以代表生物的本质属性#cod#x02014 ...

1986

0.0

... 在进行宏基因组分类时,通常提取DNA短序列的k-mer频率来作为物种的数字特征向量,并在一个个特征向量之间寻找差异来衡量物种差别,从而在计算水平上进行宏基因组序列样本的分类^[3] ...

2011

0.0

... 现有的宏基因组分类平台,如:NBC取k=15^[4] ...

2016

0.0

... PhyloPythia平台及PhyloPythiaS,前者取k=7,后者做频率组合,分别取k=4,5,6^[5] ...

2011

0.0

... 为解决k-mer频率在分类过程中效率低的问题,Meinicke等^[6]提出GRS(Genome ReSequencing)方法,对大米宏基因组及韩国人类宏基因组的k-mer特征频率属性进行优化 ...

2015

0.0

... 刘富等^[7]提出用粗糙集的属性优化理论对k-mer特征频率进行优化 ...

2013

0.0

... Koslicki等^[8]提出用压缩感知理论对k-mer特征频率进行属性优化 ...

2012

0.0

... 非负矩阵分解(Nonnegative matrix factorization,NMF)是在矩阵中所有元素均为非负数约束条件之下的矩阵分解算法,为大规模数据处理的研究提供了一个新思路^[9] ...

2010

0.0

... 从计算的传统角度看,矩阵分解结果中存在负值是合理的,但负值元素在某些实际问题中是没有意义的^[10] ...

2014

0.0

... 反之,采用非负矩阵分解方法就可以避免这一点^[11] ...

2016

0.0

... 本文首先提取DNA序列的k-mer频率特征向量,再对特征向量进行有效的优化,从原始特征向量中去除冗余信息,筛选出一个最优特征子集作成为物种标签,最后再利用聚类算法^{[12,13,14,15,16]}进行分类 ...

2017

0.0

2016

0.0

2017

0.0

... 为了验证本文所提分类策略的性能,将FCM方法与本文方法以及文献[15]中的宏基因组分类方法MetaCluster3 ...

2016

0.0

2011

0.0

... 因此,某一k长度子序列的出现频率便可与它反向互补序列的出现频率合二为一,经上述操作,能将特征向量 F的维数减少一半左右^[17] ...

2013

0.0

... Alsop等^[18]证明,当k=7时,k-mer频率可以较好地兼顾稳定性和计算效率 ...

2016

0.0

... 3 聚类完成特征优化之后,进行聚类分析验证,本文采用模糊C均值(Fuzzy C-means,FCM)算法^[19,20]对优化之后的数据进行聚类分析 ...

2017

0.0

... 3 聚类完成特征优化之后,进行聚类分析验证,本文采用模糊C均值(Fuzzy C-means,FCM)算法^[19,20]对优化之后的数据进行聚类分析 ...

2012

0.0

... 2 评价指标本文使用文献[21]的3个标准,即准确率、召回率、F率来评价所提方法的聚类性能 ...