基于改进的标签传播算法的网络聚类方法

引用本文

桂春, 黄旺星. 基于改进的标签传播算法的网络聚类方法[J].吉林大学学报（工学版）, 2018,48(5): 1600-1605
GUI Chun, HUANG Wang-xing. Network clustering method based on improved label propagation algorithm[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1600-1605 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20171019
Permissions

基于改进的标签传播算法的网络聚类方法

桂春¹, 黄旺星²

1.西北民族大学数学与计算机科学学院,兰州 730030

2.武汉大学电子信息学院,武汉 430072

作者简介:桂春(1981-) 女,副教授,博士研究生.研究方向:复杂网络,数据挖掘.E-mail:guichun2103@163.com

基金:甘肃省地区科学基金项目(61562075);西北民族大学甘肃省一流学科专项经费项目;中央高校基本科研业务费专项项目(31920180119)

摘要

采用传统标签传播算法实现网络聚类时,由于标签初始分配过程随机、节点选择过程随机、且标签更新顺序随机的原因,影响聚类结果。为此,提出一种新的基于改进标签传播算法的网络聚类方法,即用图对网络进行描述,并为网络聚类提供基础。改进标签传播算法过程如下:求出网络中任意两节点拥有最大公共邻居的平均阶数,把相似性最高的节点和邻居节点看作初始核心社团,为其分配初始标签;引入基于随机游走的相似度矩阵,令节点选择和自身相似度最高的节点拥有的标签;通过H指数对标签算法更新顺序进行改进;依据改进后结果,按照标签传播算法网络聚类过程实现聚类。实验结果表明,本文所提的网络聚类方法具有更高的准确性和稳定性。

关键词: 计算机应用; 节点; 标签; 传播算法; 网络聚类; 相似度

中图分类号:TP301 文献标志码:A 文章编号:1671-5497(2018)05-1600-06

Network clustering method based on improved label propagation algorithm

GUI Chun¹, HUANG Wang-xing²

1.School of Mathematics and Computer Science, Northwest University for Nationalities, Lanzhou 730030, China

2.School of Electronic Information, Wuhan University, Wuhan 430072,China

Abstract

Using traditional label propagation algorithm in network clustering, the initial allocation of taps, the node selection and updating order of the labels are all random processes, which affect the clustering results. To overcome this problem, a new method of network clustering based on improved label propagation algorithm is proposed, in which the graph is used to describe the network and provide the basis for the network clustering. The process of the improved label propagation algorithm includes the following steps. First, the average malpractice in the network order of any two nodes with the largest common neighbor number is obtained. Second, the most similar node and neighbor node are taken as the initial core community and its initial label is assigned. Third, the random walk similarity matrix is introduced based on the node selection and the label of the node with the highest similarity. Fourth, by using the H index on the label algorithm, the update order is improved. Finally, according to the improved result, the clustering process is realized according to the clustering process of the label propagation algorithm network. Experimental results show that the proposed network clustering method has higher accuracy and stability.

Keyword: computer application; node; label; propagation algorithm; network clustering; similarity

文章图片

0 引言

当前很多系统都以网络的形式存在, 而且复杂程度高^[1]。网络簇结构为网络最关键的拓扑结构属性, 为了描述网络中真实的簇结构, 需研究一种有效的网络聚类方法, 为研究网络拓扑结构、理解网络功能、发现网络中的规律及预测网络行为提供重要应用价值。有效的网络聚类方法在其他应用性网络中也有很高的应用前景, 不但是计算机领域亟需研究的重点课题, 也吸引了其他学科的众多研究者^[2]。

有关网络聚类的研究近年来有很大的进展, 当前网络聚类方法主要包括图分割法、W-H法、层次聚类法和标签传播算法^[3]。图分割法被广泛应用于计算机领域, 依据迭代对分原理, 把网络划分成两个最佳子图, 再不断对子图进行分割, 直到子图个数满足既定条件^[4]。图分割法的弊端为每次仅可把网络划分成两部分, 为了得到有效聚类结果需不停迭代, 实现过程复杂。W-H法任意选择两个不同社区节点, 将其设置成电压是1的初始点与电压是0的结束点, 剩余节点将获取各自电压值, 把电压值基本相同的节点分配至相同社区, 从而实现网络聚类^[5]。该方法的弊端是在分配前需掌握网络结构的先验信息。层次聚类法通过节点间的相似关系对网络进行聚类, 然而层次聚类法通常会忽略大量相似度很低的点, 导致聚类结果准确性较低^[6]。标签传播算法和以上几种方法相比, 无需掌握网络结构或先验知识, 根据网络传播特征即可实现网络聚类, 所以效率很高。但标签传播算法在传播时, 由于标签初始分配过程随机, 当相邻节点标签出现相同高频率时, 会随机选择一个标签, 且标签更新顺序随机, 影响聚类结果。为此, 本文提出了一种新的基于改进标签传播算法的网络聚类方法。

1 本文方法

1.1 网络描述

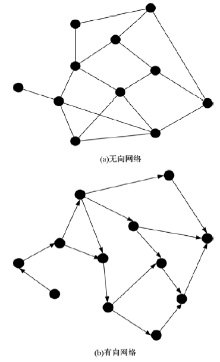
本文采用图方式对网络进行描述, 用图对网络进行描述有很高的应用价值, 不但能够描述网络, 而且是网络聚类的基础。将网络记作 $G = (U, E),$ 其中, $U$ 表示网络中全部节点的集合; $E$ 表示网络中全部边的集合。两节点间相连的线即为网络的边, 若 $(i, j)$ 与 $(j, i)$ 描述的是同一条边, 则认为该网络为无向的, 如图1(a)所示; 若描述的不是同一条边, 则认为该网络为有向的, 如图1(b)所示。

	Figure Option View Download New Window
	图1 网络描述Fig.1 Network description

1.2 标签传播算法网络聚类

采用标签传播算法对网络进行聚类处理的基本思想为:依据网络的传播特征完成对网络节点标签信息的传播, 以获取潜在网络结构, 将结构相似的网络划分至一类。首先为所有节点赋予初始标签, 然后在标签的传播过程中对节点标签进行更新, 认为标签一致的节点属于相同网络^[7]。标签传播算法易于实现, 复杂度低, 被广泛应用。

采用标签传播算法实现网络聚类详细过程如下:

(1)为网络中所有节点赋予唯一初始标签, 对其所处网络进行标记, 通常将数字或字母看作标签。

(2)完全标签信息的传播与更新处理。在进行迭代时, 全部被更新的节点标签均被其相邻节点出现次数最多的标签替代, 也就是所有节点均需与其大部分相邻节点标签保持一致。若某节点相邻节点中存在若干标签出现次数相同且达到最大的情况, 则随机选择一个标签作为该节点标签。不断迭代更新, 直到所有节点标签均保持不变, 则停止迭代。

(3)全部标签相同的节点属于相同网络。

图2描述的是标签传播过程图。

	Figure Option View Download New Window
	图2 标签传播过程图Fig.2 Label propagation process diagram

标签的更新主要包括两种类型, 分别是同步更新和异步更新^[8]。其中, 同步更新可采用下式描述:

$L_{u} (k) = f (L_{u_{k}} (k - 1), \dots, L_{u_{n}} (k - 1)) (1)$

式中: $L_{u} (k)$ 为第 $k$ 次迭代时节点 $u$ 的标签; $f$ 为一函数, 其返回值为与节点 $u$ 相邻的全部节点中相同个数最多的标签, 此种标签最少存在一个, 若 $f$ 返回的标签多于一个, 则随机挑出一个标签完成对节点 $u$ 的更新。

同步更新存在一定的弊端, 在二分图内容易导致震荡现象发生^[9]。为了确保更新具有较好的收敛性, 一般选用异步更新策略。异步更新的数学表达式为:

$\begin{array}{l} L_{u} (k) = f (L_{u_{i 1}} (k), \dots, L_{u_{im}} (k), \\ L_{u_{i (m + 1)}} (k - 1), \dots, L_{u_{in}} (k - 1)) (2) \end{array}$

标签传播算法时间效率高, 初始化时为全部节点分配标签的时间复杂度为 $C (r),$ 每次迭代的时间复杂度为 $C (s),$ 经大量研究表明, 一般仅需5次迭代更新即可获取准确的网络聚类结果, 所以标签传播算法网络聚类时间复杂度为C(s)。

分析标签传播算法可知, 标签传播算法能够解决传统算法在处理大规模网络时的时间复杂度问题, 无需预先掌握先验知识, 且不需要设计目标函数, 依据网络传播特征充分满足网络特点。然而, 在标签传播算法中, 网络中所有节点在初始时均会被赋予唯一标签, 传播时完成动态标签更新, 将会造成很多零散的、孤立的小社区出现, 导致真正网络无法聚类。因为所有节点仅有一个标签, 部分影响力较小的节点在传播时会受影响力较大的节点的影响, 导致标签传播过程出现消耗资源的逆流现象。不仅如此, 在某节点相邻节点有很多符合条件的候选标签时, 将随机选择标签, 导致网络聚类稳定性降低, 大量随机性叠加将使若干次实验结果有很大的不同。除此之外, 标签传播算法最大的弊端是节点更新顺序也完全随机。下面针对上述弊端, 采用改进的标签传播算法实现网络聚类。

1.3 改进标签传播算法

1.3.1 初始化过程改进

本节主要针对标签传播算法的初始化过程进行改进, 求出网络中任意两节点拥有最大公共邻居的平均阶数, 把相似性最高的节点和K阶邻居K节点看作初始核心社团, 为其分配初始标签。

网络中K值的确定通常取决于网络自身的特性, 公式描述如下:

$\bar{K} = \frac{\sum_{i \neq j} K_{\max} |M (i) ⋂ M (j)|}{M (M - 1) / 2} (3)$

式中: $K_{\max} |M (i) ⋂ M (j)|$ 为节点 $i$ 与节点 $j$ 间存在最大相同邻居数阶数, 网络中 $K$ 值表示网络中全部点对彼此间的平均值。

详细改进过程为:

(1)对全部点对的K阶公共邻居集进行运算。

(2)挑出存在最大公共K阶邻居的点对。当求取相似度时, 把存在最大相似度的点对以及它的K阶公共邻居当成首个初始核心社团, 同时对标签赋值。

(3)为网络中的每一个节点都分配一个标签, 作为社区的标识, 表示所处社区, 按照标签的顺序对网络中的节点进行排序, 按照排序结果组建集合 $V 。$

(4)针对集合 $V$ 中没有编号的节点, 按照步骤(2)获取另一个子结构, 并对该子结构内的节点按序编号。

(5)重复此过程, 直至集合 $V$ 中没有编号的节点均不符合 $S (u_{1}, u_{2}) \geq ε 。$ 其中, $S (u_{1}, u_{2})$ 为相邻节点 $u_{1}$ 与 $u_{2}$ 间的相似度; $ε$ 为节点的相似性指标, 且ε ∈ [0, 1]。

(6)将网络 $G$ 划分成 $N$ 个社团 $B_{1}, B_{2}, \dots, B_{N},$ 若随机挑出的两个社团符合 $|B_{i} ⋂ B_{j}| \geq \frac{1}{2} |B_{i} ⋃ B_{j}|,$ 则将这两个社团合并在一起。

通过上述过程获取部分局部核心子结构, 将其看作初始核心社团, 同时将其看作初始标签, 也是标签传播的初始点。

1.3.2 节点标签选择

为了控制节点标签选择方向, 本文引入基于随机游走的相似度矩阵, 节点更新标签时会选择和自身相似度最高的节点拥有的标签。

初始时把随机游走的步行者置于图中任意节点, 令其依据马尔科夫性质随机选择下一位置^[10]。用 $P_{ij}$ 描述一步内步行者从节点 $i$ 行至节点 $j$ 的概率, 用 $Q_{ij} (m)$ 描述步行者行走 $m$ 步时从节点 $i$ 行至节点 $j$ 的概率, 用 $Q_{i} (m)$ 描述 $Q (m)$ 矩阵第 $i$ 列的列矩阵, 则有:

$\begin{array}{l} P_{ij} = λ_{ij} / δ_{i} (4) \\ Q_{i} (m) = P^{T} Q_{i} (m - 1) (5) \end{array}$

式中: $δ_{i}$ 为节点 $i$ 的出度; $P^{T}$ 为矩阵 $P$ 的转置。对于参数 $λ_{ij}$ 而言, 若节点 $i$ 与 $j$ 间存在连接, 则 $λ_{ij}$ 取1; 若节点 $i$ 与 $j$ 间不存在连接, 则 $λ_{ij}$ 取0。

对节点 $i$ 与 $j$ 间的相似度进行计算, 公式描述为:

$S_{i, j} (m) = \frac{λ_{i}}{2 |Z|} \cdot Q_{ij} (m) + \frac{λ_{j}}{2 |Z|} \cdot Q_{ji} (m) (6)$

式中: $|Z|$ 为网络中节点间的全部连接数。

假设 $i$ 与 $j$ 为相同网络距离间隔较短的两个节点, 二者相似度较高, 但步行者在很大程度上会行至间隔较远的节点, 导致测定的 $i$ 与 $j$ 间相似度较低。为了避免这一缺陷, 可连续若干次释放步行者, 再对标签传播相似度进行叠加处理, 叠加后距离公式可描述成:

$D_{ij} (m) = \overset{m}{\sum_{t = 1}} S_{i, j} (t) (7)$

针对某固定网络, 其总边数 $|Z|$ 是保持不变的, 所以在计算时不考虑 $2 |Z|,$ 得到一种新的相似度, 将其称作OSRW相似度:

$S'_{ij} (m) = λ_{i} \cdot Q_{ij} (m) + λ_{j} \cdot Q_{ji} (m) (8)$

以 $Δm = 1$ 连续不断释放 $m$ 个步行者, 直到最后一个步行者步数为1, 对应OSRW相似度可描述为:

$S_{ij}^{*} (m) = \overset{m}{\sum_{t = 1}} S_{ij}^{t} (t) (9)$

1.3.3 更新顺序改进

标签传播算法中节点更新顺序是随机的, 若依据设定顺序进行更新, 则将大大提高网络聚类稳定性。H指数为信息计量学中体现学者贡献的指标^[11], 可有效衡量节点重要性, 所以本节通过H指数对标签算法更新顺序进行改进。节点H指数可描述为:

$H (i) = H (q_{j 1}, q_{j 2}, \dots, q_{j w_{i}}) (10)$

式中: $w_{i}$ 为节点 $i$ 的相邻连接节点数量; $q_{j 1}, q_{j 2}, \dots, q_{j w_{i}}$ 为节点 $i$ 的相邻连接节点的度。

对节点的局部影响力进行分析, 这里将采用归一化的度值作为节点 $i$ 的局部影响力, 公式描述如下:

$I (i) = \frac{q (i)}{\max \{q (j) |d (j \in U)\}} (11)$

式中: $q (i)$ 为节点 $i$ 的度。

节点 $i$ 在网络中的重要性指标 $R (i)$ 为:

$R (i) = H (i) + I (i) (12)$

节点 $u$ 相邻连接节点中存在的全部标签 $v$ 的影响力为:

$F (v) = \sum_{x \in N^{v} (u)} R (x) (13)$

式中: $N^{v} (u)$ 为节点 $u$ 的相邻连接节点集。针对节点 $u$ , 它的标签定义如下:

$y_{u} = argmax F (v) (14)$

2 实验结果分析

实验部分对本文所提的基于改进标签传播算法的网络聚类方法进行验证, 实验结果取100次运行均值。

实验数据集选择LFR基准网络数据集和真实网络数据集, LFR网络为典型的人工形成测试数据集, 将节点数量设置为800, 平均节点度设置为30, 网络混合系数依次取0.4、0.5、0.6和0.7。真实网络数据集随机选择4个典型网络:Karate、Dolphin、Jazz和Email。

实验选用NMI、模块度两个指标对网络聚类结果进行衡量^{[12, 13, 14]}。模块度为网络结构和与其有相同期望度序列的随机网络间的差异, 模块度越高, 聚类结果越准确, 计算公式如下:

$Q = \sum_{i} (b_{ij} - a_{i}^{2}) (15)$

式中: $b_{ij}$ 为网络结构期望度; $a_{i}^{2}$ 为随机网络期望度。

NMI可通过下式求出:

$NMI = \frac{- 2 \sum_{i, j} N_{i, j} \log (N_{i, j} N / N_{i \cdot} N_{\cdot j})}{\sum_{i} N_{i \cdot} \log (N_{i, j} N) + \sum_{j} N_{\cdot j} \log (N_{\cdot j} N)} (16)$

式中: $N$ 为混合矩阵; $N_{i, j}$ 为 $i 、 j$ 两个类中公共节点数量; $N_{i \cdot} 、 N_{\cdot j}$ 分别为 $N$ 中第 $i$ 行和第 $j$ 列之和; NMI是通过聚类获取的网络聚类结果和真实网络结构相似性的体现, 其值范围为[0, 1], 且越趋近于1, 聚类结果和实际结果越一致。

在LFR基准网络中, 混合系数越低, 网络结构越简单。混合系数为0.4和0.5时, 网络结构较为明显, 混合系数为0.6和0.7时, 网络结构较为复杂。将克隆方法和人工免疫方法作为对比, 比较3种方法对LFR基准网络数据集的NMI指标和模块化指标, 如表1和表2所示。

表1 三种方法针对LFR基准网络的NMI比较结果 Table 1 NMI comparison results of three methods for LFR reference network

表2 三种方法针对LFR基准网络的模块度比较结果 Table 2 Modularity comparison of three methods for LFR baseline network

分析表1和表2可知, 在网络结构较为简单的情况下, 3种方法网络聚类NMI与模块度指标相差不大。但是, 随着混合系数的逐渐增加, 网络结构越来越复杂, 与克隆方法、人工免疫方法相比, 本文方法在NMI和模块度上均有很大的提高, 在混合系数达到0.7的情况下, 克隆方法、人工免疫方法NMI和模块度均低于0.1, 已经失去了网络聚类的意义, 然而本文方法仍可有效聚类, 说明本文方法聚类效果佳。

真实数据集网络结构较为复杂, 针对Karate、Dolphin网络进行了NMI与模块度的比较, Jazz和Email因为无已知网络结构, 仅进行模块度的比较。3种方法比较结果分别用表3和表4进行描述。

表3 三种方法针对真实网络的NMI比较结果 Table 3 Comparison results of three methods for real network NMI

表4 三种方法针对真实网络的模块度比较结果 Table 4 Comparison results of three methods for real network module degree

分析表3与表4可知, 在真实数据集的4个网络中, 本文方法在模块度上明显高于人工免疫方法和克隆方法, 在Karate、Dolphin网络中, 本文方法NMI比人工免疫方法和克隆方法也明显更高, 说明本文方法网络聚类结果比其他两种方法更加稳定和准确。

3 结束语

提出了一种新的基于改进标签传播算法的网络聚类方法。用图对网络进行描述, 给出了采用标签传播算法实现网络聚类详细过程。针对标签传播算法的弊端进行了改进, 依据改进后结果, 按照标签传播算法网络聚类过程实现聚类。实验结果表明, 本文提出的网络聚类方法的准确性和稳定性更高。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	孙生才, 范菁, 陈明木, 等. 基于H指数的改进标签传播算法研究[J]. 云南民族大学学报: 自然科学版, 2017, 26(4): 317-321. Sun Sheng-cai, Fan Jing, Chen Ming-mu, et al. Research on improved label propagation algorithm based on H-index[J]. Journal of Yunnan Minzu University(Natural Science Edition), 2017, 26(4): 317-321. [本文引用:1]
[2]	郝晓丽, 张靖. 基于改进自适应聚类算法的RBF神经网络分类器设计与实现[J]. 计算机科学, 2014, 41(6): 260-263. Hao Xiao-li, Zhang Jing. Design and implementation of RBF neural network classifier based on improved adaptive clustering algorithm[J]. Computer Science, 2014, 41(6): 260-263. [本文引用:1]
[3]	陈羽中, 方明月, 郭文忠. 面向微博热点话题发现的多标签传播聚类方法研究[J]. 模式识别与人工智能, 2015, 28(1): 1-10. Chen Yu-zhong, Fang Ming-yue, Guo Wen-zhong. Research on multi-label propagation clustering method for micro-blog hot topic discovery[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(1): 1-10. [本文引用:1]
[4]	张健沛, 邓琨, 杨静, 等. 基于边标签传播的复杂网络社区识别方法[J]. 电子学报, 2015, 43(6): 1113-1118. Zhang Jian-pei, Deng Kun, Yang Jing, et al. Community identification method based on link label propagation in complex networks[J]. Electronic Journal, 2015, 43(6): 1113-1118. [本文引用:1]
[5]	孙沁瑶, 谢涛, 于重重, 等. 图像标签传播标注算法的研究[J]. 计算机仿真, 2016, 33(8): 229-233. Sun Qin-yao, Xie Tao, Yu Chong-chong, et al. Research on image label propagation annotation algorithm[J]. Computer Simulation, 2016, 33(8): 229-233. [本文引用:1]
[6]	张康, 顾幸生. 基于近邻传播的改进组搜索优化聚类算法[J]. 系统仿真学报, 2015, 27(9): 2066-2074. Zhang Kang, Gu Xing-sheng. Improved group search optimization clustering algorithm based on neighborhood propagation[J]. System Simulation Journal, 2015, 27(9): 2066-2074. [本文引用:1]
[7]	夏磊, 张乐君, 国林, 等. 节点相似度标签传播在社会网络中的应用研究[J]. 计算机工程与应用, 2014, 50(14): 103-109. Xia Lei, Zhang Le-jun, Guo Lin, et al. Application of node similarity label propagation in social network[J]. Computer Engineering and Application, 2014, 50(14): 103-109. [本文引用:1]
[8]	王旭仁, 李娜, 何发镁, 等. 基于改进聚类算法的网络舆情分析系统研究[J]. 情报学报, 2014, 33(5): 530-537. Wang Xu-ren, Li Na, He Fa-mei, et al. Research on network public opinion analysis system based on improved clustering algorithm[J]. Journal of Information, 2014, 33(5): 530-537. [本文引用:1]
[9]	汪西莉, 蔺洪帅. 最小代价路径标签传播算法[J]. 计算机学报, 2016, 39(7): 1407-1418. Wang Xi-li, Lin Hong-shuai. Minimum cost path label propagation algorithm[J]. Journal of Computer Science, 2016, 39(7): 1407-1418. [本文引用:1]
[10]	喻金平, 郑杰, 梅宏标. 基于改进人工蜂群算法的K均值聚类算法[J]. 计算机应用, 2014, 34(4): 1065-1069. Yu Jin-ping, Zheng Jie, Mei Hong-biao. K mean clustering algorithm based on improved artificial bee colony algorithm[J]. Computer Application, 2014, 34(4): 1065-1069. [本文引用:1]
[11]	唐丹, 张正军, 王俐莉. 基于改进的近邻传播聚类算法的Gap统计研究[J]. 计算机技术与发展, 2017, 27(1): 182-185. Tang Dan, Zhang Zheng-jun, Wang Li-li. Gap statistical research based on improved near neighbor propagation clustering algorithm[J]. Computer Technology and Development, 2017, 27(1): 182-185. [本文引用:1]
[12]	陈季梦, 陈佳俊, 刘杰, 等. 基于结构相似度的大规模社交网络聚类算法[J]. 电子与信息学报, 2015, 37(2): 449-454. Chen Ji-meng, Chen Jia-jun, Liu Jie, et al. Clustering algorithm for large scale social networks based on structural similarity[J]. Journal of Electronics and Information, 2015, 37(2): 449-454. [本文引用:1]
[13]	王永, 万潇逸, 陶娅芝, 等. 基于K-medoids项目聚类的协同过滤推荐算法[J]. 重庆邮电大学学报: 自然科学版, 2017, 29(4): 521-526. Wang Yong, Wan Xiao-yi, Tao Ya-zhi, et al. Collaborative filtering recommendation algorithm based on K-medoids item clustering[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2017, 29(4): 521-526. [本文引用:1]
[14]	杨玉梅. 基于信息熵改进的 K-means 动态聚类算法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(2): 254-259. Yang Yu-mei. Improved K-means dynamic clustering algorithm based on information entropy[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2016, 28(2): 254-259. [本文引用:1]

2017

0.0

... 0 引言当前很多系统都以网络的形式存在,而且复杂程度高^[1] ...

2014

0.0

... 有效的网络聚类方法在其他应用性网络中也有很高的应用前景,不但是计算机领域亟需研究的重点课题,也吸引了其他学科的众多研究者^[2] ...

2015

0.0

... 有关网络聚类的研究近年来有很大的进展,当前网络聚类方法主要包括图分割法、W-H法、层次聚类法和标签传播算法^[3] ...

2015

0.0

... 图分割法被广泛应用于计算机领域,依据迭代对分原理,把网络划分成两个最佳子图,再不断对子图进行分割,直到子图个数满足既定条件^[4] ...

2016

0.0

... W-H法任意选择两个不同社区节点,将其设置成电压是1的初始点与电压是0的结束点,剩余节点将获取各自电压值,把电压值基本相同的节点分配至相同社区,从而实现网络聚类^[5] ...

2015

0.0

... 层次聚类法通过节点间的相似关系对网络进行聚类,然而层次聚类法通常会忽略大量相似度很低的点,导致聚类结果准确性较低^[6] ...

2014

0.0

. 2014, 50(14):103-109 DOI:doi:10.3778/j.issn.1002-8331.1207-0390

Application of node similarity label propagation in social network

节点相似度标签传播在社会网络中的应用研究

Xia Lei , Zhang Le-jun , Guo Lin

夏磊, 张乐君, 国林

In recently years, detecting communities of social networks has made considerable progress, and has been widely applied in the social networks, World Wide Web, biological networks and many other fields. For the hot issues of community detection in social network, firstly the correlate clustering algorithms based on local information are studied and summarized. Secondly, the label propagation algorithm that is short for Label Propagation Algorithm（LPA） is researched and analyzed in-depth, in order to solve the drawback of the algorithm which the network partition is always not optimal due to the random strategy of LPA, this paper introduces the concept of similarity of node attributes, and proposes label propagation algorithm on the basis of the similarity of node attributes called LPA-SNA（Label Propagation Algorithm based on the Similarity of Node Attributes） for short. Finally, taking the American College football network, DBLP co-researchers network as data set, the paper achieves the original label propagation algorithm and improves label propagation algorithm based on the similarity of node attributes respectively, and compares their performance. Experimental results show that the label propagation algorithm based on the similarity of node attributes is more effective compared with the original label propagation algorithm, which not only enhances quality of the network clustering, optimizes the clustering results, but also reduces the time overhead of the algorithm and improves clustering speed.

近年来，社会网络簇结构挖掘取得了长足的进展，广泛应用在社会网、生物网和万维网等领域中。针对当前研究社会网络簇结构挖掘的热点问题，重点研究基于局部信息的聚类算法，并进行分析总结；对标签传播算法（LPA）进行深入研究与分析，针对该算法中由于随机策略而导致网络划分并非最优的缺陷，引入节点属性相似度的概念，提出LPA-SNA算法；采用美国大学足球赛程网络、科学家合著网络作为数据集，分别实现LPA算法与LPA-SNA算法，并对它们的性能进行比较。实验结果表明LPA-SNA较之原始的LPA算法，提高了网络聚类的质量，优化了聚类效果，同时降低了算法的时间开销，提高了算法聚类速度。

... 首先为所有节点赋予初始标签,然后在标签的传播过程中对节点标签进行更新,认为标签一致的节点属于相同网络^[7] ...

2014

0.0

. 2014, 33(5):530-537 DOI:doi:10.3772/j.issn.1000-0135.2014.05.008

Research on network public opinion analysis system based on improved clustering algorithm

基于改进聚类算法的网络舆情分析系统研究

Wang Xu-ren , Li Na , He Fa-mei

王旭仁, 李娜, 何发镁

摘　要：针对互联网舆情挖掘领域的特点，提出了一种基于向量空间模型VSM的文本聚类算法STCC（Similarity Threshold Control Clustering BasedVSM）。该算法按照层次聚类从下至上凝聚的策略，获取初始簇信息，然后根据K-means算法的思想以设置的聚类相似度阈值作为度量来合并簇。该算法结合层次聚类和K-means算法的优点，克服其缺点。与层次聚类相比，每一次聚类时不需要比较所有簇之间的相似度，降低了时间复杂度，提高了聚类的效率；与K—means算法相比，不需要确定K值，灵活性更高。通过实验表明，该算法聚类效果好，实用性高，适合大规模的文本聚类。

... 标签的更新主要包括两种类型,分别是同步更新和异步更新^[8] ...

2016

0.0

. 2016, 39(7):1407-1418

Minimum cost path label propagation algorithm

最小代价路径标签传播算法

Wang Xi-li , Lin Hong-shuai

汪西莉, 蔺洪帅

... 同步更新存在一定的弊端,在二分图内容易导致震荡现象发生^[9] ...

2014

0.0

. 2014, 34(4):1065-1069 DOI:doi:10.11772/j.issn.1001-9081.2014.04.1065

K mean clustering algorithm based on improved artificial bee colony algorithm

基于改进人工蜂群算法的K均值聚类算法

Yu Jin-ping , Zheng Jie , Mei Hong-biao

喻金平, 郑杰, 梅宏标

In order to overcome the disadvantages of the K-Means Clustering (KMC) algorithm, such as the poor global search ability, being sensitive to initial cluster centroid, as well as the initial random, being vulnerable to trap in local optima and the slow convergence velocity in later period of the original Artificial Bee Colony (ABC) algorithm, an Improved ABC (IABC) algorithm was proposed. IABC algorithm adopted the max-min distance product algorithm for initial bee colony to form a fitness function, which is adapted to the KMC algorithm, and a position updating method based on the global leading to enhance the efficiency of the iterative optimization process. The combination of the IABC and KMC (IABC-Kmeans) would improve the efficiency of clustering. The simulation experiments were conducted on the four standard test functions including Sphere, Rastrigin, Rosenbrock and Griewank and the UCI standard data sets. The experimental results indicate that IABC algorithm has a fast convergence speed, and overcomes the defect of the original algorithm being easily falling into local optimal solution; IABC-Kmeans has better clustering quality and general performance.

针对K均值聚类(KMC)算法全局搜索能力差、初始聚类中心选择敏感,以及原始人工蜂群(ABC)算法的初始化随机性、易早熟、后期收敛速度慢等问题，提出了一种改进人工蜂群算法(IABC)。该算法利用最大最小距离积方法初始化蜂群,构造出适应KMC算法的适应度函数以及一种基于全局引导的位置更新公式以提高迭代寻优过程的效率。将改进的人工蜂群算法与KMC算法结合提出IABC-Kmeans算法以改善聚类性能。通过Sphere、Rastrigin、Rosenbrock和Griewank四个标准测试函数和UCI标准数据集上进行测试的仿真实验表明，IABC算法收敛速度快，克服了原始算法易陷入局部最优解的缺点；IABC-Kmeans算法则具有更好的聚类质量和综合性能。

... 初始时把随机游走的步行者置于图中任意节点,令其依据马尔科夫性质随机选择下一位置^[10] ...

2017

0.0

. 2017, 27(1):182-185

Gap statistical research based on improved near neighbor propagation clustering algorithm

基于改进的近邻传播聚类算法的Gap统计研究

Tang Dan , Zhang Zheng-jun , Wang Li-li

唐丹, 张正军, 王俐莉

... H指数为信息计量学中体现学者贡献的指标^[11],可有效衡量节点重要性,所以本节通过H指数对标签算法更新顺序进行改进 ...

2015

0.0

. 2015, 37(2):449-454 DOI:doi:10.11999/JEIT140512

Clustering algorithm for large scale social networks based on structural similarity

基于结构相似度的大规模社交网络聚类算法

Chen Ji-meng , Chen Jia-jun , Liu Jie

陈季梦, 陈佳俊, 刘杰

To cluster the directed and large-scale social networks, a Structural Clustering Algorithm for Directed Networks (DirSCAN) and a corresponding Parallel algorithm (PDirSCAN) are proposed. Considering oriented behavioral relation between two vertices, DirSCAN is constructed based on action structural similarity and function analysis. To meet the need of large-scale social network analysis, a lossless PDirSCAN based on MapReduce distributed parallel architecture is designed to improve the processing performance. A large number of experimental results on real-world network datasets show that DirSCAN improves performance of SCAN up to 2.34% on F1, PDirSCAN runs 1.67 times faster than DirSCAN.

针对社交网络的有向交互性和大规模特性，该文提出一种基于结构相似度的有向网络聚类算法(DirSCAN)，以及相应的分布式并行算法(PDirSCAN)。考虑社交网络中节点间的有向交互性，将行为结构相似的节点聚集起来，并进行节点功能分析。针对社交网络规模巨大的特点，提出MapReduce框架下的分布式并行聚类算法，在确保聚类结果一致的前提下，提高处理性能。大量真实数据集上的实验结果表明，DirSCAN比无向网络聚类算法(SCAN)在F1上可提高2.34%的性能，并行算法PDirSCAN比DirSCAN运行速度提升1.67倍，能够有效处理大规模的有向网络聚类问题。

... 实验选用NMI、模块度两个指标对网络聚类结果进行衡量^[12,13,14] ...

2017

0.0

. 2017, 29(4):521-526 DOI:doi:10.3979/j.issn.1673-825X.2017.04.015

Collaborative filtering recommendation algorithm based on K-medoids item clustering

基于K-medoids项目聚类的协同过滤推荐算法

Wang Yong , Wan Xiao-yi , Tao Ya-zhi

王永, 万潇逸, 陶娅芝

摘　要：针对传统协同过滤推荐算法通常针对整个评分矩阵进行计算,存在效率不高的问题,提出一种基于K-medoids项目聚类的协同过滤推荐算法。该算法根据项目的类别属性对项目进行聚类,构建用户的偏好领域,使用用户偏好领域内的评分矩阵进行用户间相似度的计算,得到目标用户的最近邻居集,并生成推荐结果。与常用的Kmeans聚类方法相比,采用K-medoids方法对项目类别属性进行聚类,不仅克服了评分聚类可靠性不高的问题,而且算法还具有更好的鲁棒性。实验结果表明,该算法能有效提高推荐质量。

... 实验选用NMI、模块度两个指标对网络聚类结果进行衡量^[12,13,14] ...

2016

0.0

. 2016, 28(2):254-259

Improved K-means dynamic clustering algorithm based on information entropy

基于信息熵改进的 K-means 动态聚类算法

Yang Yu-mei

杨玉梅

... 实验选用NMI、模块度两个指标对网络聚类结果进行衡量^[12,13,14] ...