作者简介:刘元宁(1962-),男,教授,博士生导师.研究方向:虹膜识别.E-mail:lyn@jlu.edu.cn
为了抑制虹膜噪声并提高算法通用性,提出在虹膜识别中运用高斯拉普拉斯(Log)算子与自适应优化伽柏(Gabor)滤波。Log算子抑制虹膜噪声,40组频率和方向各不同的Gabor滤波提取虹膜特征,将特征转化为二进制特征编码。滤波参数用变异粒子群优化(MPSO)算法针对不同虹膜库进行自适应优化。通过计算虹膜间的汉明(Hamming)距离判定虹膜类别。与其他Gabor滤波和机器学习类算法相比,该算法可以有效抑制虹膜噪声干扰进而提高识别正确率,同时算法在多种虹膜库识别的通用性更好。
To suppress iris noise and improve algorithm versatility, it is proposed to use Laplacian of Gaussian (LOG) operator and adaptive optimization Gabor filtering in iris recognition. The LOG operator suppresses iris noise and 40 sets of Gabor filtering with different frequencies and directions extract iris features and transform the features into binary feature codes. The filtering parameters are adaptively optimized for different iris libraries using Mutation Particle Swarm Optimization (MPSO) algorithm. The iris category is determined by calculating the Hamming distance between irises. Compared with other Gabor filtering and machine learning algorithm, the proposed algorithm can effectively suppress iris noise interference and improve recognition accuracy. At the same time, this algorithm has higher versatility in recognition of various iris libraries.
虹膜识别技术因其稳定性、唯一性、非入侵性[1, 2]等特点成为当今生物识别技术研究的热门方向。虹膜识别过程分为虹膜图像采集、虹膜预处理、虹膜特征表达与匹配[3]3个步骤。关于虹膜特征提取与匹配, Daugman[4]提出了利用伽柏(Gabor)滤波提取虹膜特征, 用Hamming距离进行虹膜分类的方法。之后Gabor滤波提取虹膜特征算法被多次改进, 例如, 李欢利等[5]提出了基于加权Gabor滤波器的虹膜识别算法。Field[6]则利用Log-Gabor滤波进行虹膜识别。唐荣年等[7]提出将Log-Gabor滤波与多分辨率结合的方式进行虹膜识别。但这些方法在单独使用的情况下, 对不同的虹膜库的通用性较差。为了让Gabor滤波可以根据不同虹膜库自适应的改变参数, Zhou等[8]提出用粒子群优化算法(PSO)对Gabor滤波的参数进行优化。虽然可以优化Gabor参数, 但PSO也容易造成局部最优[9]的问题, 所得到的参数可能不理想。除此之外, 虹膜的纹理信息也受到噪声的干扰, 妨碍虹膜特征的提取。
本文提出了基于高斯拉普拉斯(Log)算子与自适应参数优化伽柏(Gabor)滤波的虹膜识别算法。用Log算子处理图像, 尽可能减少噪声干扰。通过变异粒子群优化算法(MPSO)来优化Gabor滤波参数, 不仅使参数可以跳出局部最优, 还使Gabor滤波可以针对不同的虹膜库进行参数的自适应调整, 增加算法的通用性。最后利用40组方向、频率不同的Gabor滤波提取虹膜特征, 将纹理信息转换为由二进制特征码, 通过计算汉明距离辨别虹膜类别。
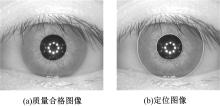
虹膜图像的预处理主要包括虹膜质量评价、虹膜定位和虹膜归一增强。首先, 通过多指标分步质量评价法判定虹膜可以进行虹膜识别[9]。之后采用微积分圆模板法[10]定位出虹膜的有效区域。质量合格图像如图1(a)所示, 定位图像如图1(b)所示。
最后, 使用橡皮圈模型法[11]归一虹膜图像, 将环形虹膜展开成一个512× 64维度的矩形。增强图像纹理[12], 并从左上角截取256× 32维度的截取纹理最强部分作为虹膜识别区域, 完成虹膜的归一增强。图1的全环归一图像如图2(a)所示, 虹膜识别区域如图2(b)所示。
Gabor滤波的表达式[13]如下:
式中:
令
为了得到不同的方向
式中:
因为图像的边缘可以看作是位于一阶导数较大的像素处。因此, 可以通过图像的一阶导数来确定图像的边缘。但由于图像易受到噪音干扰, 并且噪音点处一阶导数也可以得到极大值。而求解极大值的过程也比较复杂。高斯算子可以很好地抑制噪音[14], 并且, 一阶导数极大值的二阶导数是0。
使用高斯拉普拉斯(Log)算子的过程就是先用高斯算子对截取增强虹膜图像进行高斯模糊, 抑制噪音的干扰, 再用拉普拉斯算子求二阶导数, 二阶导数等于0处对应的像素就是图像的边缘, 这样的处理可以将虹膜纹理边缘更加清晰地呈现出来。图2(b)的Log处理图像如图3所示(为更好显示纹理信息, 图3图像显示的是处理后图像灰度值反转后的结果)。
特征提取之前, 先对所有归一化虹膜图像进行水平移位消除虹膜旋转[15]。特征提取时, 将5种频率、8种方向的Gabor滤波器按照角度从小到大、频率从低到高的顺序编号为G1~G40。5种频率按从低到高的顺序编号为F0~F4。8种方向按照角度从小到大的顺序编号为J0~J7。然后, 将256× 32大小的经Log算子处理过的图像分成32个32× 8大小的子块。每个子块用编号G1~G40的Gabor滤波器进行滤波处理, 计算每个子块的所有滤波结果的幅度值。求出每个子块幅度值相应最大的频率和方向, 将频率和方向分别按编号编码为3位二进制码, 并以频率在前、方向在后的顺序拼接在一起, 将每个子块特征编写成6位特征编码, 记作
式中:
利用Hamming距离将提取的虹膜特征编码与训练样本中的虹膜特征编码进行比较。
Hamming距离是最常用的匹配算法, 利用特征编码相应位置上编码不同的数量与编码位数之间的比值作为两个特征模板之间的匹配度, 距离越小, 两个特征模板就越匹配[16]。Hamming距离公式如下:
式中:
将计算好的Hamming距离与设定的分类阈值进行比较, 若小于分类阈值, 则将测试虹膜和训练虹膜归属于同一类别。
通过变异粒子群优化算法对Gabor滤波的
使用30个粒子, 每个粒子的初始速度范围为[-50, 50], 每个粒子包含一组需要优化的Gabor滤波参数, 即相当于运用了30组初始Gabor滤波。粒子初始值中
针对具体某一虹膜库, 取测试虹膜5张, 同类别, 异类别训练虹膜各10张, 运用上文提及的虹膜特征提取算法, 计算测试虹膜和训练虹膜之间的Hamming距离, 进而计算适应度, 适应度函数如下:
式中:T为适应度;HDi为与测试虹膜不同类别的第i张虹膜的海明距离;HDs为与测试虹膜相同类别的虹膜的第2张海明距离。
因为距离越小, 两个虹膜就越匹配。因此, 适应度公式的目的是为了寻找相同类别和不同类别之间区分度最大的参数, 进而在多类别的虹膜识别中可以有效地排除不同类别以及找到相同类别, 尽可能避免因为相似度过近导致的错误匹配和错误拒绝的问题。
通过300次迭代, 每次计算新的适应度T,若新的T小于原来的T,那么将新的个体的历史最优pBest设为新的T对应的滤波参数,而30组滤波器中T最小的值对应的滤波参数设为新的群体最优gBest。新的pBest和gBest确定后,对每个粒子i的第d维的速度和位置进行粒子的进化:
若每次进化结束后未达到结束条件, 就再计算各个粒子的适应度函数值, 直到可以输出gBest。上述公式中,ω为惯量权重,设为0.729;c1和c2为加速系数,设为1.49445[17];$rand^{d}_{1}$和$rand^{d}_{2}$为两个[0,1]区间上的随机数;$v^{d}_{i}$为粒子速度$x^{d}_{i}$为粒子大小。
每个粒子进化时, 设置一个变异算子[18], 因为kmax变化范围为[0, 2π ], 变异效果不明显, 所以只针对频率间隔进行变异, 在粒子进化为新的粒子时, 根据变异概率
随迭代次数的增多, 以及优化的深入, 最后Gabor滤波参数的寻优值会稳定在某一个值附近。通过这样的方式, 针对不同的虹膜库设置不同的参数值, 进而提高算法的通用性。
用表示错误拒绝率(False reject rate, FRR)及错误接收率(False accept rate, FAR)关系的ROC曲线评价虹膜识别算法, 而FRR与FAR的值称为等错率(Equal error rate, EER)。EER越小, ROC曲线越接近坐标轴, 虹膜识别算法的性能越好。正确识别率(Correct recognition rate, CRR)也是评价虹膜识别算法性能的指标之一[19]。本文均使用最高CRR, 最低EER以及ROC曲线对虹膜识别算法进行评价。
本实验使用的CPU主频为双核2.5 GHz, 内存为8 GB, 操作系统为Windows XP。
本文使用Gabor滤波进行特征提取及分类, 并用Log算子对虹膜的噪音进行处理, 与其他机器学习类的虹膜识别算法相比, 本文算法具有更大的优势。将本文算法与常用的基于SVM的虹膜识别算法[20, 21], 基于神经网络的虹膜识别算法[22], 以及混合k-最近邻域分类器算法[23]进行了比较。
同样是用Gabor提取虹膜特征, 与Hamming距离阈值法相比, 传统的SVM算法[24, 25, 26]虽然可以提高识别准确率, 但是采集环境不同所带来的图像噪音会对图像准确率造成影响, 并且, 参数值的设定也会对虹膜的正确识别造成影响。另外在时间上, Hamming距离阈值法也比SVM要快, 比较适合多类别虹膜识别的快速响应。本文以吉林大学JLU-3.0虹膜库为例[27], 进行对比实验。
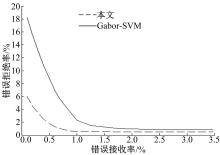
选取虹膜库中的60类别, 每个类别图像为20张, 图像都是质量评价合格的图像。类内比较654次, 类外比较4630次。Gabor滤波优化后的最大频率为0.4959 , 频率间隔为1.4586。SVM算法中的Gabor不使用滤波参数优化算法。本文算法和SVM识别算法的CRR、EER的比较结果如表1所示。ROC曲线如图4所示。
| 表1 CRR和EER实验结果 Table 1 Experimental results of CRR and EER |
从图4和表1可以看出, 虽然本算法和SVM识别算法均具有较低的EER, CRR也比较高, 但还是本文算法的效果要更好。
本实验的测试虹膜库类别数均在120个类别以内, 每个类别虹膜库均不超过20张图像, 属于小型虹膜库。以上述JLU-3.0虹膜库为例, 将本文算法与SVM算法和混合k-最近邻域分类器算法进行对比实验, 将同一测试虹膜与虹膜库中同样的1200张虹膜图像进行匹配, 3种算法的运行时间t以及CRR如表2所示。
| 表2 运行时间和CRR实验结果 Table 2 Experimental results of runing time and CRR |
由表2可知, 本文算法正确率更高, 对于相同数量的虹膜识别, 耗费时间更短, 响应速度更快。
与神经网络识别算法相比, 本文在自适应虹膜库上可以做到更胜一筹。传统的人工神经网络的结构以及连接权重等目前没有通用性算法确定[28], 通常是根据经验人为训练, 步骤繁琐并且难以保证结构的最优。本文根据不同的虹膜库自适应的训练参数, 进而达到一个较好的状态进行虹膜识别。
根据对比实验可知:在小规模虹膜库(120类别以内, 每类别不超过20张图像)有噪声干扰的条件下的虹膜识别上, 本文算法更适合用于虹膜识别, 更具有实用性。
使用JLU-3.0虹膜库、中国科学院CASIA-V1、CASIA-Iris-Interval、CASIA-Iris-Twins作为测试虹膜库[29], 并且所取虹膜图像都是经过质量评价为合格的图像。
将本文算法(Log+MPSO)与参数未优化的Gabor滤波、只使用PSO算法的Gabor滤波、文献[30]提出的基于混沌算子的粒子群算法(CPSO)的Gabor滤波进行对比。
每种算法在每个虹膜库所进行的类间、类外以及总匹配次数如表3所示。各虹膜库在MPSO优化前Gabor滤波参数的初始值及优化后的寻优值如表4所示。
| 表3 不同虹膜库匹配次数 Table 3 Number of different iris libraries matches |
| 表4 参数的初始值和寻优值 Table 4 Initial value and optimal value |
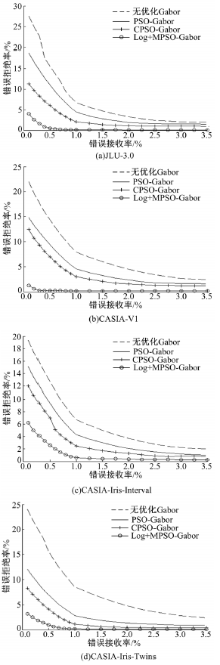
各个虹膜库的CRR与EER如表5所示。各虹膜库的ROC曲线如图5所示。
| 表5 各个虹膜库的CRR与EER Table 5 CRR and EER of each iris library |
根据表5和图5可知, 与其他Gabor滤波算法相比, 本文算法的正确识别率在不同虹膜库中是4种算法中最高的, EER是最低的。分析这种现象的原因如下:
(1)图像采集本身的噪声干扰确实已经达到影响虹膜识别的地步, 采用Log算子抑制噪声干扰后, 提取到的虹膜特征更加的纯粹, 减少了不必要的冗余, 进而提高了正确识别率。
(2)相对于不优化的Gabor滤波, 本文通过MPSO算法针对不同的虹膜库对Gabor进行自适应参数优化, 使相同结构的Gabor滤波可以更加适应该虹膜库进行虹膜识别, 提高了Gabor滤波识别算法在不同虹膜上的通用性。
(3)变异粒子群优化算法(MPSO)与粒子群优化算法(PSO)的本质在于增加了对变异区间所起作用的判断, 进而及时扩大寻优区间。粒子群寻优最初需要设置寻优区间, 粒子在该区间内进行寻优, 但寻优区间设置具有一定的随机性, 无法完全保证该寻优区间是最佳寻优区间, 而变异算子的存在就是为了让寻优区间发生突变, 使粒子有机会跳出既定轨道进行新的参数寻优。同时, 通过设定迭代次数, 既保证了全局搜索的完全, 又使搜索的收敛性得到满足。
(4)通过加入混沌算子提高粒子群的随机性, 比单独的粒子群优化算法要好很多, 但是混沌算子的设定具有一定的规律, 比完全随机变异算子的混沌性要低一些。同时, 混沌算子是常态的, 这也增加了粒子从最优寻优区间跳出到非最优寻优区间, 并难以返回的可能性。而变异是非常态的, 偶发的, 这也使其跳出最优寻优区间的可能性较低, 并且也更容易返回最优寻优区间, 可塑性较高。
由此可以得出结论:本文算法的正确识别率较高, 等错率较低, ROC曲线更贴近于横纵坐标轴, 同时在多虹膜库识别中可以保持较高的稳定性, 鲁棒性较好。
为抑制虹膜噪声干扰并提高Gabor滤波算法在不同虹膜库上的通用性, 提出了基于高斯拉普拉斯算子与自适应优化伽柏滤波的虹膜识别算法。利用Log算子抑制虹膜图像的噪声干扰, 用不同方向和频率的滤波组对虹膜进行滤波处理, 并用变异粒子群优化算法优化Gabor滤波参数, 使Gabor滤波的结构可以针对不同虹膜库进行识别, 提高了Gabor滤波识别算法的通用性。计算Hamming距离判定虹膜所属类别。使用多种小规模虹膜库对该算法进行评价, 在同等运行条件下, 与其他Gabor滤波算法和机器学习类虹膜算法相比, 该算法可以有效抑制图像噪声干扰, 提高虹膜识别的正确识别率, 降低等错率, ROC曲线更加贴近横纵坐标轴, 具有更好的鲁棒性与稳定性, 同时提高了Gabor算法在不同虹膜库的通用性。本文的重点放在了对虹膜噪声的抑制上, 对于光照不均的问题考虑不周, 另外, 针对其他类型的分类方法在虹膜识别领域的应用, 也将是未来的工作重点。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|