基于NSCT变换和相似信息鲁棒主成分分析模型的图像融合技术

引用本文

刘哲, 徐涛, 宋余庆, 徐春艳. 基于NSCT变换和相似信息鲁棒主成分分析模型的图像融合技术[J].吉林大学学报（工学版）, 2018,48(5): 1614-1620
LIU Zhe, XU Tao, SONG Yu-qing, XU Chun-yan. Image fusion technology based on NSCT and robust principal component analysis model with similar information[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1614-1620 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170928
Permissions

基于NSCT变换和相似信息鲁棒主成分分析模型的图像融合技术

刘哲¹, 徐涛², 宋余庆¹, 徐春艳¹

1.江苏大学计算机科学与通信工程学院, 江苏镇江 212013

2.吉林大学机械科学与工程学院,长春 130022

作者简介:刘哲(1982-),女,副教授,博士.研究方向:图像处理与分析.E-mail:1000004088@ujs.edu.cn

基金:国家自然科学基金项目(61772242,61572239,61402204); 江苏大学高级人才科研启动基金项目((14JDG141); 江苏高校“青蓝工程”项目

摘要

针对传统的图像处理是以单个像素点为基础进行融合而忽略了信息的相似性以及存在信息丢失的问题,提出了基于非下采样Contourlet变换(Nonsubsampled contourlet transform, NSCT)和相似信息鲁棒主成分分析(Robust principle component analysis, RPCA)模型的图像融合技术。首先对源图像获取图像块构造初始矩阵,通过对构造矩阵进行NSCT分解获得高频和低频部分,利用提出的具有相似信息低秩矩阵模型将低频成分分解成低秩矩阵和稀疏误差矩阵,再分别对两幅图像的低秩矩阵、稀疏误差矩阵及高频成分采用绝对值最大法融合规则进行融合,最后通过逆变换得到融合图像。MRI和CT的脑部图像的实验分析结果表明,本文算法可以更好地保留源图像中的边缘和纹理信息。

关键词: 图像处理; 图像融合; 非下采样Contourlet变换; 鲁棒主成分分析; 低秩矩阵

中图分类号:TP391.4 文献标志码:A 文章编号:1671-5497(2018)05-1614-07

Image fusion technology based on NSCT and robust principal component analysis model with similar information

LIU Zhe¹, XU Tao², SONG Yu-qing¹, XU Chun-yan¹

1.School of Computer Science and Communication Engineering,Jiangsu University,Zhenjiang 212013,China

2.College of Mechanical Science and Engineering, Jilin University,Changchun 130022,China

Abstract

In traditional medical image fusion process based on single pixel, the information similarity is ignored and detailed information may loss. To solve these problems, an image fusion technology based on Nonsubsampled Contourlet (NSCT) and Robust Principal Component Analysis (RPCA) model with similar information is proposed. First, the initial matrix constructed by the image block from the original images is decomposed into low frequency and high frequency parts by NSCT transformation. Second, the low rank component is decomposed into low rank matrix and spare error matrix by using the low rank matrix model with similar information. Third, the low rank matrix of the two images, the spare error matrix and high-frequency components are fused by fusion rule of the absolute maximum method. Finally the fusion image is replaced by the inverse transform. The experiment results on CT and MRI show that the proposed method can maintain more edge and texture detailed information of the source images.

Keyword: image processing; image fusion; Nonsubsampled contourlet transform(NSCT); robust principal component analysis; low-rank matrix

文章图片

0 引言

医学图像处理在疾病的诊断与临床的治疗中起着不可或缺的促进作用。传统的单模态成像设备已经不能够为临床医生对疾病做出正确地临床诊断提供足够的有效信息, 为了提高临疾病诊断准确率, 多模态医学图像融合技术应运而生^[1]。

近年来, 稀疏表示, 低秩表示, 压缩感知在医学图像处理领域中得到了广泛应用。Yin^[2]提出了基于多尺度字典学习的稀疏表示图像融合方法, 此方法基于多尺度平稳小波结构, 使用一致学习策略学习平稳小波子带的子字典。Yin等^[3]提出了新的基于多目标稀疏表示的图像融合方法。Liu等^[4]对基于多尺度分解和稀疏表示的图像融合框架进行研究, 模型分析了稀疏表示, 并对不同的多尺度方法相结合的融合性能进行比较, 实验结果表明这种方法在针对不同的源图像时需要不同多尺度分解方法。Ren等^[5]提出了基于压缩感知和低秩矩阵分解的超分辨率图像融合方法。由压缩感知理论推广发展而来的低秩矩阵恢复, 也成为近些年来的研究热点。在医学图像融合领域, Wang等^[6]提出了基于各向异性热扩散和低秩结构分析的多模态医学图像融合算法。该算法通过构造图像金字塔, 使用分而治之的方法嵌入多层次图像属性来计算各向异性热核, 用低秩表示来获得低阶分量信息特征的尺度空间, 其中噪声可以自然地同步解耦, 最后用相应的融合策略对分解的尺度空间进行融合。

利用低秩表示图像融合方法具有显示信息准确性和鲁棒性的优势, 并考虑到图像信息之间的相关性, 提出了基于相似信息鲁棒主成分分析模型的医学图像融合算法。首先构造基于相似信息鲁棒主成分分析模型, 通过NSCT进行多分辨率变换, 根据构建的模型将低频成分分解成低秩矩阵和稀疏误差矩阵, 再分别对图像的低秩矩阵、稀疏误差矩阵及高频成分采用绝对值最大法融合规则进行融合, 最后逆变换得到融合图像。实验结果表明本文算法可以更好地保留源图像的信息。

1 相关理论

1.1 鲁棒主成分分析(RPCA)

近几年来, 低秩矩阵恢复(Low-rank matrix recovery, LRMR)成为继压缩感知和稀疏表示以来的另一个研究热点^{[7, 8, 9]}。低秩矩阵恢复主要是从较大的但稀疏的误差中恢复出其本质的低秩的数据矩阵^[10]。目前, 低秩矩阵恢复主要包括鲁棒主成分分析(Robust principle component analysis, RPCA)、矩阵补全(Matrix completion, MC)和低秩表示(Low-rank representation, LRR)三类模型^[11]。

John Wright提出了鲁棒主成分分析模型(RPCA)研究如何从包含较大的稀疏噪声数据的数据中恢复出本质的低秩数据^[12]。其模型如下:

$\{\begin{array}{l} \min_{Z, E} rank (Z) + λ ‖ E ‖_{0} \\ s.t. D = Z + E \end{array} (1)$

式中: $λ (λ > 0)$ 是折中因子; $D$ 对应的是观测数据矩阵; $Z$ 为低秩矩阵部分; $E$ 是稀疏的噪声数据矩阵, 则观测数据矩阵 $D$ 可以写成 $D = Z + E 。$ 因为上述问题式(1)是个非凸优化问题, 是NP难问题, 直接对其求解困难, 故需要对式(1)进行松弛处理。采用矩阵的核范数来替代矩阵的秩函数, 用矩阵 $I_{1}$ 范数来替换矩阵 $I_{0}$ 范数。根据矩阵的 $I_{2, 1}$ 范数, 故而模型的凸优化形式如下:

$\{\begin{array}{l} \min_{Z, E} ‖ Z ‖_{*} + λ ‖ E ‖_{2, 1} \\ s.t. D = Z + E \end{array} (2)$

其中矩阵的核函数 $‖ \cdot ‖_{*}$ 为矩阵的奇异值之和, 而‖ E‖ _{2, 1}=∑ _j $\sqrt[]{\sum_{i} (E_{i, j})^{2}}$ 。目前RPCA模型已经在背景建模、图像对齐、视频监控等应用研究中, 显示出了有效性与优越性。

1.2 NSCT变换

NSCT变换能实现离散的多尺度、多方向的图像分解^{[14, 15, 16]}, 是由非下采样金字塔分解结构(NSP)和非下采样方向滤波器组(NSDFB)两部分组成。由NSP实现图像的多分辨率分解, 分解成高频和低频部分; 由NSDFB实现多方向分解, 将高频部分分解为2的任意次幂个方向子带, 并且各子带大小与源图像相同, 因此NSCT变换具有平移不变性。分解示意图如图1所示。

	Figure Option View Download New Window
	图1 NSCT变换结构Fig.1 Structure of nonsubsampled contourlet transforms

2 本文方法

2.1 基于相似信息的RPCA模型构建

为了将数据矩阵分解成低秩的主要特征信息和稀疏的显著特征信, 并且还要在在低秩特征信息里充分保留数据彼此间的相似信息, 构建结合相似信息的RPCA模型。对于含有稀疏误差信息的低秩数据矩阵, RPCA可以将矩阵 $X$ 分解成低秩部分 $Z$ 和稀疏部分 $E,$ 其模型可以表示为:

$X = Z + E (3)$

为了达到分解的效果, 需要对 $Z$ 的秩最小化处理, 而 $E$ 需要稀疏化, 求解模型表示为:

$\{\begin{array}{l} \min_{Z, E} rank (Z) + λ ‖ E ‖_{0} \\ s.t. X = Z + E \end{array} (4)$

式(4)是一个高度非凸优化问题, 是NP难的, 直接求解比较困难, 因此需要对其进行松弛处理。得到以下模型:

$\{\begin{array}{l} \min_{Z, E} ‖ Z ‖_{*} + λ ‖ E ‖_{2, 1} \\ s.t. X = Z + E \end{array} (5)$

式中: $X$ 对应的是观测数据矩阵。但是模型缺少对空间信息的有效利用, 可能会造成数据的细节信息的丢失。为此, 在模型的基础上加入对图像之间的相似信息。

对于数据矩阵 $X = [x_{1}, x_{2}, \dots, x_{n}],$ 其中 $x_{i} 对应的是第 i$ 个图像块, 如果图像块 $x_{i}$ 与图像块 $x_{j}$ 之间具有一定的相似性, 那么在低秩矩阵 $Z$ 中也应该保留这样的相似信息, 即 $z_{i}$ 和 $z_{j}$ 也有一定的相似性。为此引入相似度的概念, 设 $W$ 为其权重矩阵, 定义如下:

$W_{ij} = \exp \{- \frac{‖ x_{i} - x_{j} ‖_{2}^{2}}{σ}\} (6)$

为了能够获得图像块 $x_{i}$ 与图像块 $x_{j}$ 的相似信息, 可以通过最小化下面的函数达到目的:

$\begin{array}{l} \frac{1}{2} \overset{mn}{\sum_{i, j = 1}} ‖ Z_{i} - Z_{j} ‖_{2}^{2} w_{ij} = \\ \overset{mn}{\sum_{i = 1}} {Z^{T}}_{j} Z_{i} D_{ii} - \overset{mn}{\sum_{i = 1}} {Z^{T}}_{j} Z_{i} W_{ij} = \\ tr (ZD Z^{T}) - tr (ZW Z^{T}) \\ = tr (ZL Z^{T}) (7) \\ 其中 \\ D_{ii} = \overset{mn}{\sum_{J}} W_{ij} (8) \\ L = D - W (9) \end{array}$

式中: $tr (*)$ 是矩阵的迹; 矩阵 $D$ 是对角矩阵; $L$ 则是拉普拉斯矩阵。

则本文提出的基于相似信息的RPCA的模型可以表示为:

$\{\begin{array}{l} \min_{Z, E} ‖ Z ‖_{*} + λ ‖ E ‖_{2, 1} + β \times tr (ZL Z^{T}) \\ s.t. X = Z + E \end{array} (10)$

下面将给出模型(10)的求解方法以及相应的算法描述。

2.2 基于相似信息的RPCA模型的求解

已知模型是凸优化问题, 具有唯一解。如果直接求解模型较为困难, 因此引入了一个新的矩阵 $J,$ 将其转换成一个等价问题:

$\{\begin{array}{l} \min_{Z, E} ‖ J ‖_{*} + λ ‖ E ‖_{2, 1} + β \times tr (JL J^{T}) \\ s.t. D = Z + E, Z = J \end{array} (11)$

采用增广拉格朗日乘子法(ALM)对式(11)进行求解。先为其构造增广拉格朗日函数:

$\begin{array}{l} (J, E, Y_{1}, Y_{2}, μ) = \\ ‖ J ‖_{*} + λ ‖ E ‖_{2, 1} + β \times tr (JL J^{T}) + \\ tr ({Y^{T}}_{1} (D - Z - E)) + tr ({Y^{T}}_{2} (Z - J)) + \\ \frac{μ}{2} (‖ D - Z - E ‖_{F}^{2} + ‖ Z - J ‖_{F}^{2}) (12) \end{array}$

式中: $Y_{1}$ 和 $Y_{2}$ 是拉格朗日乘子; $μ (μ > 0)$ 是惩罚因子。下面采用交替迭代方法求解(12)中的各个变量。

(1)首先固定变量 $A, E, N, Y_{1}, Y_{2}$ 和 $μ,$ 更新 $J,$ 即:

$\begin{array}{l} J_{(k + 1)} = argmi n_{J} ‖ J ‖_{*} + β \times tr (JL J^{T}) + \\ tr ({Y^{T}}_{2} (A - J)) + \frac{μ}{2} ‖ A - J ‖_{F}^{2} = \\ argmi n_{J} ‖ J ‖_{*} + \\ \frac{μ}{2} {(J - (J_{K} - \frac{1}{η} [\begin{array}{l} J_{K} (\frac{2 β}{μ} L + I) - \\ (A + \frac{Y_{2}}{μ}) \end{array}])}_{F}^{2} (13) \end{array}$

(2)接着固定变量 $J, E, Y_{1}, Y_{2}$ 和 $μ,$ 更新 $A,$ 即:

$\begin{array}{l} A_{k + 1} = argmi n_{A} tr ({Y^{T}}_{1} (D - A - E)) + \\ tr ({Y^{T}}_{2} (A - J)) + \\ \frac{μ}{2} (‖ D - A - E ‖_{F}^{2} + ‖ A - J ‖_{F}^{2}) = \\ \frac{1}{2} (D - E + J + \frac{Y_{1}}{μ} - \frac{Y_{2}}{μ}) (14) \end{array}$

(3)再固定变量 $J, A, Y_{1}, Y_{2}$ 和 $μ,$ 更新 $E,$ 即:

$\begin{array}{l} E_{k + 1} = \\ argmi n_{E} λ ‖ E ‖_{2, 1} + tr ({Y^{T}}_{1} (D - A - E)) + \\ \frac{μ}{2} ‖ D - A - E ‖_{F}^{2} = \\ argmi n_{E} λ ‖ E ‖_{2, 1} + \frac{μ}{2} {(E - (D - A + \frac{Y_{1}}{μ}))}_{F}^{2} (15) \end{array}$

(4)再固定变量 $J, A, E$ 和 $μ,$ 更新拉格朗日乘子 $Y_{1}$ 和 $Y_{2} :$

$\begin{array}{l} Y_{1, k + 1} = Y_{1, k} + μ_{k} (D - A_{k + 1} - E_{k + 1}) (16) \\ Y_{2, k + 1} = Y_{2, k} + μ_{k} (A_{k + 1} - J_{k + 1}) (17) \end{array}$

(5)更新惩罚因子 $μ$ :

$μ_{k + 1} = \min (ρ μ_{k}, μ_{\max}) (18)$

式中: $ρ > 1$ 是常数。

下面给出具体的算法流程, 如下所示。

算法1:结合相似信息的鲁棒主成分分析模型

输入:数据矩阵 $X,$ 折中参数 $λ 、 β;$

输出:低秩主要特征信息 $Z,$ 稀疏显著特征信息 $E$

初始化: $J = 0, Z = 0, E = 0, Y_{1} = 0, Y_{2} = 0, μ = 10^{- 6}, μ_{\max} = 10^{6}, ρ = 1.2, η = 2, ε = 10^{- 6} 。$

主要步骤:

(1)按照式(7)(8)(9)计算拉普拉斯矩阵 $L 。$

(2)根据式(13)更新 $J 。$

(3)根据式(14)更新 $A 。$

(4)根据式(15)更新 $E 。$

(5)根据式(16)、(17)更新 $Y_{1}$ 和 $Y_{2} 。$

(6)根据式(18)更新惩罚因子 $μ 。$

(7)检验迭代终止条件:

$‖ D - Z - E ‖_{\infty} < ε$ 且 $‖ Z - J ‖_{\infty} < ε$

重复步骤(3)~(7), 否则终止, 输出低秩主要特征信息 $Z,$ 稀疏显著特征信息 $E 。$

2.3 图像融合算法

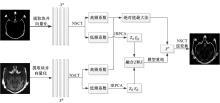
根据构建的相似信息的RPCA模型, 结合多分辨率理论, 提出了基于NSCT和改进RPCA医学图像融合算法。首先获取源图像对应的图像块矩阵, 用非下采样轮廓波对相似块进行尺度分解, 然后对低频部分采用构建新模型分解成低秩矩阵和稀疏误差矩阵, 选取合适的融合规则对分解系数进行融合, 图像融合算法流程如图2所示。

	Figure Option View Download New Window
	图2 基于NSCT和RPCA的图像融合算法流程图Fig.2 Flow chart of medical image fusion algorithm based on NSCT and RPCA

图像融合算法如下:

(1)对源图像A和源图像B进行块提取则形成新的矩阵 $X^{A}$ 和 $X^{B},$ 该矩阵是含有低秩结构的数据矩阵。

(2) $X^{A}$ 和 $X^{B}$ 通过多尺度分解得到高频和低频系数, 低频系数采用提出的低秩矩阵模型进行分解得到低秩矩阵和稀疏误差矩阵, 并分别使用绝对值最大法对 $X^{A}$ 和 $X^{B}$ 的低秩部分 $Z^{A} 、 Z^{B}$ 和稀疏部分 $E^{A} 、 E^{B}$ 进行融合得到 $Z^{F}$ 和 $E^{F} 。$

(3)高频系数部分则用绝对值最大法进行融合。

(4)将融合后的低秩部分 $Z^{F}$ 和稀疏部分 $E^{F}$ 通过的逆变换 $Z^{F} + E^{F}$ 得到新的低频系数。

(5)对高频和低频部分采用多尺度变换的逆变换得到最终的融合结果 $X^{F} 。$

3 实验结果与分析

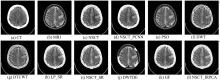
为了验证算法的有效性, 在MATLAB 2014a上进行仿真实验, 采用的实验数据是哈佛医学院的脑部图像^[17], 并利用主观和客观的评价相结合的方式对融合结果进行分析比较, 客观评价采用AG^[18]、QABF^[19]、EG^[20]、MI^[20]、Entropy^[21]评价指标。实验数据分为正常图像(见图3)和病变图像(见图4), 其中癌症选取了53岁的癫痫病患者的CT和MRI图像作为原始数据, 如图3和图4中的(a)和(b)所示, 患者组数据为20组, 正常组数据也为20组。采用经典的NSCT^[14]、NSCT_PCNN^[22]、粒子群(PSO)^[23]、离散小波变换(DWT)、双树复小波变换^[4]、LP_稀疏表示(LP_SR)^[4]、NSCT_稀疏表示(NSCT_SR)^[4]、结合小波变换和自适应分块的多聚焦图像快速融合(DWTDE)^[24], 基于方向滤波器的图像融合算法^[25]和本文算法进行比较, 如图3和4中的(c)~(l)所示。

	Figure Option View Download New Window
	图3 正常组图像融合结果Fig.3 Image fusion results of normal group

	Figure Option View Download New Window
	图4 癌症组图像融合结果Fig.4 Fusion results of cancer group

从图3直观地看, 上述的十种算法均能较好地保持源图像中的重要信息, 将两幅图像融合成一幅清晰的图像。从图3(c)和(d)可以看出NSCT算法和NSCT_PCNN算法的融合结果与本文方法结果最为接近; 图3(e)所示的PSO算法的融合图像相比其他的融合结果出现了丢失细节信息和边缘模糊的现象; 从图3(f)所示的DWT和(g)DTCWT两种算法可以发现产生了较为明显的振铃现象, 其中DWT的融合结果还呈现出块状拼接的现象; 从图3(j)和(k)可以看出, DWTDE和GF算法的融合结果均存在局部信息有所丢失的问题, 边缘结构信息不完整; 本文方法采用了NSCT进行多分辨率分解, 实现了图像的平移不变性, 从而解决了振铃现象的出现, 并且本文算法将图像的信息分解成低秩部分和稀疏误差部分, 分别代表图像的内部结构信息和显著特征信息, 同时还对图像块的相似信息加以利用, 较好地保留了原始图像中的流形结构信息, 因而取得了良好的视觉效果。

从表1的客观评价指标可知, 在AG指标上, 本文方法的值最大, 表明基于多尺度分解和低秩矩阵模型方法的融合图像最为清晰。在EG、MI、Entropy的指标值上同样是本文算法指标值最大, 意味本文方法的融合结果的信息最为丰富且边缘也最为清晰, 还原度最高。QABF的指标值上, 本文方法在指标值上同样具有优势, 表明基于多尺度分解和低秩矩阵模型的方法和源图像的细微差距最小, 能够具有更好的融合结果。

表1 正常图像不同融合方法结果比较 Table 1 Image fusion index of normal fusion results

采用患癌症的病人的脑部CT和MRI图像进行融合比较分析, 如图4所示。从图4(f)和(g)可以看出, DWT和DTCWT都具有较为明显的振铃现象, 其原因都是因为直接对图像进行上采样和下采样的操作。而经典的NSCT方法和基于NSCT方法的图像融合方法由于对采样机制的改进, 从图4中可知, 融合结果均能消除振铃。如图4(g)所示, DWTED方法未能对于轮廓边缘的信息进行很好地描述, 信息丢失比较严重。同其他方法相比, 本文算法融合图像具有更好的融合效果, 不仅对两幅源图像中的主要信息进行了有效的融合, 还有细节信息还原度高, 轮廓也更为清晰。

从客观角度进行融合比较分析, 如表2所示。从表中可知, 本文算法对于AG、EG、MI、Entropy指标综合比较表现最优, 表明本文算法融合图像的边缘信息清晰和更加丰富的图像信息。在第二组实验中, QABF与其他指标一样, 其指标值最大, 表明本文算法融合结果与源图像在细微信息的差距最小。从各项客观评价指标比较分析, 本文方法融合图像清晰水平更高, 信息也更为丰富。

表2 癌症图像不同融合方法结果比较 Table 2 Fusion index of cancer fusion results

4 结束语

针对图像融合易忽略数据之间的相似性, 提出了一个基于NSCT和相似信息模型的RPCA图像融合算法。为了能让融合图像之间能保留更多的细节相似信息, 本文在模型中引入了相似矩阵块的概念; 然后通过改进后的RPCA将NSCT分解后的低频系数将其分解为低秩矩阵和稀疏误差项, 其中低秩部分则表示图像的内部主要结构, 而稀疏误差部分为其的显著部分; 最后再采用相应的融合规则对图像进融合。为了验证本文算法的性能, 在哈佛医学院的脑部的CT和MRI图像进行仿真实验。实验结果表明, 本文算法在其细节信息还是边缘结构信息都具有更好的包含能力, 具有更好的融合性能。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Du J, Li W, Lu K, et al. An overview of multi-modal medical image fusion[J]. Neurocomputing, 2016, 215: 3-20. [本文引用:1]
[2]	Yin H. Sparse representation with learned multiscale dictionary for image fusion[J]. Neurocomputing, 2015, 148: 600-610. [本文引用:1]
[3]	Yin H, Li Y, Chai Y, et al. A novel sparse-representation-based multi-focus image fusion approach[J]. Neurocomputing, 2016, 216: 216-229. [本文引用:1]
[4]	Liu Y, Liu S, Wang Z. A general framework for image fusion based on multi-scale transform and sparse representation[J]. Information Fusion, 2015, 24: 147-164. [本文引用:4]
[5]	Ren K, Xu F. Super-resolution images fusion via compressed sensing and low-rank matrix decomposition[J]. Infrared Physics and Technology, 2015, 68: 61-68. [本文引用:1]
[6]	Wang Q, Li S, Qin H, et al. Robust multi-modal medical image fusion via anisotropic heat diffusion guided low-rank structural analysis[J]. Information Fusion, 2015, 26(C): 103-121. [本文引用:1]
[7]	Cand ès E J, Li X, Ma Y, et al. Robust principal component analysis[J]. Journal of the ACM, 2011, 58(3): 11. [本文引用:1]
[8]	Ni Y, Sun J, Yuan X, et al. Robust low-rank subspace segmentation with semidefinite guarantees[C]∥IEEE International Conference on Data Mining Workshops, IEEE, Computer Society, 2010: 1179-1188. [本文引用:1]
[9]	Liu G, Lin Z, Yan S, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 171-184. [本文引用:1]
[10]	Cand ès, Emmanuel J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9/10): 589-592. [本文引用:1]
[11]	史加荣, 郑秀云, 魏宗田, 等. 低秩矩阵恢复算法综述[J]. 计算机应用研究, 2013, 30(6): 1601-1605. Shi Jia-rong, Zheng Xiu-yun, Wei Zong-tian, et al. Survey on algorighms of low-rank matrix recovery[J]. Application Research of Computers, 2013, 30(6): 1601-1605. [本文引用:1]
[12]	刘园园. 快速低秩矩阵与张量恢复的算法研究[D]. 西安: 西安电子科技大学智能感知与图像理解教育部重点实验室, 2013. Liu Yuan-yuan. Algorithm research of fast low-rand matrix and tenser recovery[D]. Xi'an: Key Laboratory of Intelligent Perception and Image Understand ing of Ministry of Education, Xidian University, 2013. [本文引用:1]
[13]	Chand rasekaran V, Sanghavi S, Parrilo P A, et al. Rank-sparsity incoherence for matrix decomposition[J]. SIAM Journal on Optimization, 2011, 21(2): 572-596. [本文引用:1]
[14]	Cai J F, Cand S E J, et al. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982. [本文引用:2]
[15]	Cunha A L D, Zhou J, Do M N. The nonsubsampled contourlet transform: Theory Desigh, and Applications[J]. IEEE Transactions on Image Processing, 2006, 15(10): 3089-3100. [本文引用:1]
[16]	崔玲玲, 卢朝阳, 李静, 等. 基于非下采样Contourlet域高斯混合模型的布匹瑕疵识别算法[J]. 吉林大学学报: 工学版, 2013, 43(3): 734-739. Cui Ling-ling, Lu Zhao-yang, Li Jing, et al. Fabric defect recognition algorithm based on Gaussian mixture model in nonsubsampled contourlet domain[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(3): 734-739. [本文引用:1]
[17]	http://www.med.harvard.edu/AANLIB/.[2017-07-08]. [本文引用:1]
[18]	Kumar B K S. Image fusion based on pixel significance using cross bilateral filte[J]. Signal, Image and Video Processing, 2015, 9(5): 1193-1204. [本文引用:1]
[19]	Xydeas C S, Petrovic V. Objective image fusion performance measure[J]. Military Technical Courier, 2000, 36(4): 308-309. [本文引用:1]
[20]	郭雷, 李晖晖, 鲍永生. 图像融合[M]. 北京: 电子工业出版社, 2008. [本文引用:2]
[21]	Prakash O, Srivastava R, Khare A. Biorthogonal wavelet transform based image fusion using absolute maximum fusion rule[C]∥Information and Communication Technologies, IEEE, 2013: 577-582. [本文引用:1]
[22]	Jiao Z, Shao J, Xu B. A Novel Multi-focus Image Fusion Method Using NSCT and PCNN[M]. Berlin Heidelberg: Springer, 2012: 161-170. [本文引用:1]
[23]	Niu Y, Shen L. The optimal multi-objective optimization using PSO in blind color image fusion[C]∥International Conference on Multimedia & Ubiquitous Engineering, IEEE Computer Society, 2007: 970-975. [本文引用:1]
[24]	刘羽, 汪增福. 结合小波变换和自适应分块的多聚焦图像快速融合[J]. 中国图象图形学报, 2013, 18(11): 1435-1444. Liu Yu, Wang Zeng-fu. Multi-focus image fusion based on wavelet transform and adaptive block[J]. Journal of Image and Graphics. 2013, 18(11): 1435-1444. [本文引用:1]
[25]	Li S, Kang X, Hu J. Image fusion with guided filtering[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2013, 22(7): 2864-2875. [本文引用:1]

2016

0.0

... 传统的单模态成像设备已经不能够为临床医生对疾病做出正确地临床诊断提供足够的有效信息,为了提高临疾病诊断准确率,多模态医学图像融合技术应运而生^[1] ...

2015

0.0

... Yin^[2]提出了基于多尺度字典学习的稀疏表示图像融合方法,此方法基于多尺度平稳小波结构,使用一致学习策略学习平稳小波子带的子字典 ...

2016

0.0

... Yin等^[3]提出了新的基于多目标稀疏表示的图像融合方法 ...

2015

0.0

... Liu等^[4]对基于多尺度分解和稀疏表示的图像融合框架进行研究,模型分析了稀疏表示,并对不同的多尺度方法相结合的融合性能进行比较,实验结果表明这种方法在针对不同的源图像时需要不同多尺度分解方法 ...

... 采用经典的NSCT^[14]、NSCT_PCNN^[22]、粒子群(PSO)^[23]、离散小波变换(DWT)、双树复小波变换^[4]、LP_稀疏表示(LP_SR)^[4]、NSCT_稀疏表示(NSCT_SR)^[4]、结合小波变换和自适应分块的多聚焦图像快速融合(DWTDE)^[24],基于方向滤波器的图像融合算法^[25]和本文算法进行比较,如图3和4中的(c)~(l)所示 ...

2015

0.0

... Ren等^[5]提出了基于压缩感知和低秩矩阵分解的超分辨率图像融合方法 ...

2015

0.0

... 在医学图像融合领域,Wang等^[6]提出了基于各向异性热扩散和低秩结构分析的多模态医学图像融合算法 ...

2011

0.0

... 1 鲁棒主成分分析(RPCA)近几年来,低秩矩阵恢复(Low-rank matrix recovery, LRMR)成为继压缩感知和稀疏表示以来的另一个研究热点^[7,8,9] ...

2010

0.0

... 1 鲁棒主成分分析(RPCA)近几年来,低秩矩阵恢复(Low-rank matrix recovery, LRMR)成为继压缩感知和稀疏表示以来的另一个研究热点^[7,8,9] ...

2013

0.0

... 1 鲁棒主成分分析(RPCA)近几年来,低秩矩阵恢复(Low-rank matrix recovery, LRMR)成为继压缩感知和稀疏表示以来的另一个研究热点^[7,8,9] ...

2008

0.0

... 低秩矩阵恢复主要是从较大的但稀疏的误差中恢复出其本质的低秩的数据矩阵^[10] ...

2013

0.0

... 目前,低秩矩阵恢复主要包括鲁棒主成分分析(Robust principle component analysis, RPCA)、矩阵补全(Matrix completion, MC)和低秩表示(Low-rank representation, LRR)三类模型^[11] ...

2013

0.0

... John Wright提出了鲁棒主成分分析模型(RPCA)研究如何从包含较大的稀疏噪声数据的数据中恢复出本质的低秩数据^[12] ...

2011

0.0

2010

0.0

... 2 NSCT变换NSCT变换能实现离散的多尺度、多方向的图像分解^[14,15,16],是由非下采样金字塔分解结构(NSP)和非下采样方向滤波器组(NSDFB)两部分组成 ...

2006

0.0

... 2 NSCT变换NSCT变换能实现离散的多尺度、多方向的图像分解^[14,15,16],是由非下采样金字塔分解结构(NSP)和非下采样方向滤波器组(NSDFB)两部分组成 ...

2013

0.0

... 2 NSCT变换NSCT变换能实现离散的多尺度、多方向的图像分解^[14,15,16],是由非下采样金字塔分解结构(NSP)和非下采样方向滤波器组(NSDFB)两部分组成 ...

0.0

... 3 实验结果与分析为了验证算法的有效性,在MATLAB 2014a上进行仿真实验,采用的实验数据是哈佛医学院的脑部图像^[17],并利用主观和客观的评价相结合的方式对融合结果进行分析比较,客观评价采用AG^[18]、QABF^[19]、EG^[20]、MI^[20]、Entropy^[21]评价指标 ...

2015

0.0

2000

0.0

2008

0.0

2013

0.0

2012

0.0

2007

0.0

2013

0.0

2013

0.0