引用本文
欧阳继红, 李双, 孙伟, 富倩. 运动对象间的方位关系推理方法. 2014, 44(1): 117-123
OUYANG Ji-hong, LI Shuang, SUN Wei, FU Qian. Reasoning method of orientation relation between moving objects. 吉林大学学报(工学版), 2014, 44(1): 117-123  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
运动对象间的方位关系推理方法
欧阳继红1,2, 李双1,2, 孙伟1,2, 富倩1,2
1.吉林大学 计算机科学与技术学院,长春 130012
2.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012

欧阳继红(1964),女,教授,博士生导师.研究方向:知识工程与专家系统,空间推理和数据挖掘.E-mail:ouyj@jlu.edu.cn

基金:国家自然科学基金项目(61170092,61133011,61272208,61103091, 61202308);
摘要

针对传统时空推理研究大多局限于静态空间对象以及Rupam方位关系模型ROR复合表和概念邻域图所存在的问题,提出了一种动态方位关系推理方法。首先对ROR关系模型中复合表及概念邻域图进行完善:提出了ROR关系静态推理算法,并给出了复合表;提出了一种ROR概念邻域关系自动生成算法并构建了概念邻域图;将ROR关系复合表和概念邻域图与Rupam方法进行比较,结果表明,本文方法不仅能给出Rupam所给的正确结果,还能修正Rupam方位关系模型不存在的复合结果,且复合结果和概念邻域图更完整。然后基于ROR关系复合表和概念邻域图给出了运动对象间方位关系推理方法DRA。最后通过智能家居中的应用实例,说明了DRA方法的有效性。

关键词: 人工智能; 方位关系复合表; 概念邻域图; 区间关系; 运动对象
中图分类号:TP18 文献标志码:A 文章编号:1671-5497(2014)01-0117-07
Reasoning method of orientation relation between moving objects
OUYANG Ji-hong1,2, LI Shuang1,2, SUN Wei1,2, FU Qian1,2
1.College of Computer Science and Technology, Jilin University, Changchun 130012, China
2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun, 130012, China
Fund:
Abstract

To solve the problem of limitation of traditional spatio-temporal reasoning in static space, and the problems in Rupam's orientation relation composition table and conceptual neighborhood graphs, a dynamic reasoning method based on Rupam's orientation relations model was proposed. First, the ROR base relations'composition table and conceptual neighborhood graphs are improved; a static reasoning algorithm is proposed and a ROR based relations'composition table is created; an auto-generated algorithm to produce conceptual neighborhood graphs of orientation relations is put forward. A comparison of the composition table and conceptual neighborhood graphs with those of Rupam was conducted and results show that the composition table and conceptual neighborhood graphs are more complete than Rupam's. Then a dynamic reasoning method (DRA) is proposed. To demonstrate the effectiveness of DRA, an application of smart home was illustrated based on the composition table and neighborhood graphs.

Keyword: artificient intelligence; orientation relations' composition table; conceptual neighborhood graphs; interval relations; object in motion
0 引言

现实世界中,时空知识大多随时间动态变化,且这些动态变化的时空知识在机器人导航、自动规划等领域具有广泛的应用。动态时空知识的表示与推理已逐渐成为研究热点,1992年,Freksa[ 1]首次定义了概念邻域,并将其用于时间连续性的表示和推理;同年,Cohn[ 2]等针对空间连续性给出拓扑关系的概念邻域图;2000年,Goyal[ 3]等给出了原子方向关系概念邻域图;2004年,Nico[ 4]等首次提出用概念邻域方法定性表达移动对象间相对位置和方向的关系;2008年,Marco[ 5]等采用拓扑-方向约束对表达拓扑和方向结合的空间关系,并给出了{TPP,NTPP}与原子主方向结合关系的概念邻域图;2010年,Rupam[ 6]针对两个运动对象A和B,提出左前、左且左前等25个方位关系,并同24个相对方向关系一起建模运动事件。

综上,动态时空推理研究已具备一定基础,但现有研究多数针对拓扑关系进行[ 7],针对方位关系的动态时空推理研究还不多见。已有Rupam方位关系模型ROR表达能力较强,但缺少动态方位关系推理方法,所给原子方位关系复合表和概念邻域图也存在问题。为解决上述问题,本文基于Rupam方位关系模型ROR,利用矩形关系复合定义[ 8]及Allen区间关系复合表[ 9],提出了ROR方位关系静态推理算法,给出了原子方位关系复合表;基于Freksa概念邻域结构[ 10],提出了ROR概念邻域关系自动生成算法并给出了关系的概念邻域图;随后,将ROR关系复合表和概念邻域图与Rupam方法进行了比较;最后,给出了运动对象间方位关系推理方法DRA,并用一个应用实例说明了DRA方法的有效性。

1 Rupam方位关系和概念邻域图
1.1 Rupam方位关系

基本区间关系是同一坐标轴上2个区段间所有可能成立的13种基本关系[ 9],记为 Aint={b,bi,m,mi,e,d,di,s,si,f,fi,o,oi}(见表1)。 Aint与其上的关系运算构成一代数系统,称为区间代数。区间代数在二维空间的扩展称为矩形代数[ 10],其上的关系称为矩形关系,基本矩形关系的形式化定义为 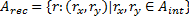。Rupam用矩形关系定义了左前、左且左前等25个方位关系(见表2),并给出了方位关系复合表及概念邻域图[ 6]。

表1 基本区间关系 Table 1 Basic interval relations
表2 矩形关系表示的25种方位关系 Table 2 Twenty-five orientation relations represented by rectangle relations
1.2 概念邻域图

1992年,Freksa[ 1]首次定义了概念邻域,并将其用于Allen时间区间关系的分析。Freksa指出,如果两个时间区间关系可以通过平滑变换而互相转换,则这两个时间区间关系可以作为概念邻域被连接起来。平滑变换有3种类型:保持区间的一个端点不动移动另一个端点;移动整个区间;延长或缩短一个区间。通过这三种平滑变换形成的概念邻域类型分别被命名为 邻域,如图1所示。

图1 区间关系的三种概念邻域结构Fig.1 Differing deformations of events induce different neighborhood structures

概念邻域结构最初的提出是用于处理时间区间代数中时间区间[ 9]连续变化的问题[ 1],而目前它已成为研究变化的定性空间关系的重要手段[ 7]。本文基于Freksa的 邻域结构,研究运动对象间方位关系的变化情况。

2 ROR关系复合表和概念邻域图
2.1 ROR关系复合表

复合是从已知的关系推导出未知关系的推理机制,它是关系代数中非常重要的一种运算,同时也是定性空间推理中非常重要的判断约束是否满足的手段。复合主要有存在性复合和相容性复合,本文ROR关系复合属于相容性复合[ 8]。

基于矩形关系复合的定义[ 8],可以求得ROR关系复合结果。首先,给出矩形关系复合的定义。在集合2Arec(2Arec为矩形关系的幂集)中,关系的复合有如下形式的定义:

定义1 R°S=⋃{(A°C)×(B°D):(A,B)∈R且(C,D)∈S},其中R,S∈2Arec,°为复合运算符[ 8]。

利用定义1,本文给出了ROR关系复合算法Composition,其思想如下:

(1)根据R°S=⋃{(A°C)×(B°D)},求出A°C以及B°D的结果,并将其分别保存在集合no1和no2中;

(2)用集合no1中的每一个元素分别与集合no2中的每一个元素做笛卡尔乘积,并在表2中查找与乘积结果所对应的方位关系,求得的所有方位关系即为两方位关系的复合结果。

算法Composition输入、输出变量的含义以及ADL描述如下:

算法Composition(orirec,n,intcom,com.result25)/*

输入、输出变量的含义:

orirec:链表数组,数组每一项保存的是某一方位关系的矩形关系表示

n:关系的数量,这里n等于25

intcom:Allen区间关系复合表

com:25种关系的字符串形式表示

result25:两方位关系的复合结果保存在result25这个数组中*/

WC1[初始化]

n ← 25.

WC2[求原子方位关系复合结果]

FOR i = 1 TO n DO(

point1 ← orirec[i]. /*链表orirec[i]的每一项保存的是第i个方位关系的一个矩形关系*/

FOR j = 1 TO n DO(

point2 ← orirec[j].

WHILE NEXT(point1) ≠ NULL DO(

WHILE NEXT(point2) ≠ NULL DO(

no1←intcom[x(NEXT(point1))][x(NEXT(point2))]./*求AoC的结果*/

no2←intcom[y(NEXT(point1))][y(NEXT(point2))]./*求BoD的结果*/

findresult(no1,no2,result25,com)./*findresult函数根据no1和no2的笛卡尔乘积来求得原子方位关系的复合结果并保存在result25中*/

point2 ← NEXT(point2).)

point1 ← NEXT(point1).

point2 ← orirec[j].

PRINT(result25)./*输出两方位关系复合结果*/)

point1 ← orirec[i].))

根据Composition算法我们得到了ROR关系完整的复合表。

2.2 ROR关系概念邻域图

两个运动对象由于运动而引起方位关系的变化通常用“概念邻域图”来描述。概念邻域图的定义如下:

定义2 在一个模型的概念邻域图中,通常用带圈的节点表示原子关系。若两个原子关系可以通过某种变换而直接变换,则这两个原子关系用一条线段或弧线连接起来。这样节点与连接节点的线段或弧线就构成了概念邻域图。

在图2中,对象P(颜色较浅的P)与参考对象R的方位关系为“F”,当对象P沿箭头方向运动时,P与R之间的方位关系会立即变为“OIF”,也就是说方位关系“F”与“OIF”可以直接转换而不需要中间变化为其他关系,那么“F”与“OIF”之间就具有概念邻域关系。将具有概念邻域关系的方位关系用线段或弧线连接起来,就构成了方位关系概念邻域图。因ROR研究的对象在运动过程中其大小、形状等属性通常不变,又因为ROR方位关系的定义是基于矩形代数的,矩形代数是区间代数在二维空间的扩展,这与Freksa提出的区间关系 B-概念邻域结构相对应,故利用Freksa的 B-概念邻域结构我们可以构建出ROR原子方位关系概念邻域图。

图2 方位关系“F”与“OIF”有概念邻域关系Fig.2 “F” is a conceptual neighbor of “OIF”

首先给出ROR概念邻域关系的自动生成算法AutoGen。AutoGen算法思想如下:

(1)将方位关系i(1≤i≤25)的rx并起来(集合意义下)保存在集合recx中,将ry并起来保存在集合recy中;

(2)将recx中所有元素的概念邻域关系并起来保存在集合cngx中,将recy的保存在集合cngy中;

(3)用cngx中每一个元素分别与recy中每一个元素做笛卡尔乘积,再在表2中查找乘积结果对应的方位关系并将其加入到集合result中。将同样的操作应用于recx和cngy;

(4)若recx与recy同时含有{m, f, s, e, mi, fi, si}中的一个或多个元素,则将recx包含的这些元素的概念邻域关系与recy包含的这些元素的概念邻域关系做笛卡尔乘积,查表2并将找到的方位关系加入到集合result中;将同样的操作应用于cngx和cngy。

算法AutoGen输入、输出变量的含义以及ADL描述如下:

算法AutoGen(orirec,CNGTable.result)/*

输入、输出变量含义:

orirec:链表数组,数组每一项保存的是某一方位关系的矩形关系表示

CNGTable:13种区间关系的概念邻域关系

result:方位关系的概念邻域关系保存在这个数组中*/

AG1[初始化]

n←25.

count←0.

AG2[求方位关系的概念邻域关系]

FOR i = 1 TO n DO(

point ← orirec[i].

WHILE NEXT(point) ≠ NULL DO(

recx[count] ← x(NEXT(point)).

recy[count] ← y(NEXT(point)).

count ← count + 1.)

FOR j = 0 TO count - 1 DO(

cngx[j] ← CNGTable[recx[j]].

cngy[j] ← CNGTable[recy[j]].)

result ← find(recx,recy,cngx,cngy). /*find函数根据算法思想的第3步求结果*/

实现算法AutoGen,我们即可构建出ROR关系概念邻域图。

3 本文方法与Rupam方法的比较

(1)Rupam所给正确的复合结果,本文也可以给出

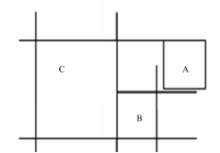
表3为Rupam所给ROR方位关系复合表。在表3中,标有数字“1”的方位关系复合结果是正确的。我们以“R”与“BR”的复合为例来说明。图3中,对象A、B间方位关系为“R”,对象B、C间方位关系为“BR”,A、C间方位关系为“FR”,说明“R”与“BR”的复合结果为“FR”。Rupam及本文都给出了这一正确的复合结果,如表3和表4所示。

图3 “R”与“BR”的复合结果为“BR”Fig.3 Composition of relation “R” and “BR”

表3 Rupam所给6种ROR原子方位关系复合表 Table 3 Rupam’s Six ROR base relations’ composition table
表4 本文的6种ROR原子方位关系复合表 Table 4 Six ROR base relations’ composition table

(2)Rupam复合表中复合结果不完整的部分,本文已补充完整

Rupam所给复合表(表3)中,标有数字“2”的方位关系复合结果是不完整的,我们以方位关系“FR”与“R”的复合为例来说明。图4中,对象A、B间方位关系为“FR”,B、C间方位关系为“R”,A、C间方位关系为“R”,说明“FR”与“R”的复合结果包含“R”。Rupam复合表中并没有给出这一复合结果,而在本文ROR方位关系复合表中给出了这一复合结果,如表4所示。

图4 方位关系“FR”与“R”的复合Fig.4 Composition of relation“FR”and“R”

(3)Rupam复合表中不正确的复合结果,在本文所给复合表中均已改正

Rupam复合表(表3)中标有数字“3”的方位关系复合结果是不正确的,我们以方位关系“BL”与“BR”的复合为例来说明。因为“BL”是由{m,b}×{m,b}定义的,即“BL”在 y轴上的投影区间关系为{m,b};同理“BR”在 y轴上投影区间关系为{m,b},“R”在 y轴上的投影区间关系为{d,s,f,e}。因不包含关系“R”。表3“BL”与“BR”的复合结果包含了“R”,而表4中却没有,说明Rupam给出的复合结果部分是错误的,而这些错误在本文所给复合中并未出现。

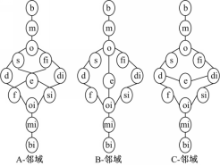
(4)本文ROR原子方位关系概念邻域图与Rupam的比较

基于算法AutoGen本文构建了ROR原子方位关系概念邻域图,如图5(a)所示。图5(b)为Rupam给出的ROR原子方位关系概念邻域图。针对图2所给实例我们可以看到,当对象P沿箭头方向运动时,P与R之间的方位关系由“F”变为“OIF”,说明“F”与“OIF”之间具有概念邻域关系,但这在Rupam的概念邻域图(图5(b))中并没有体现出。而从图5(a)中可以看到“F”与“OIF”之间有邻域关系,说明本文构建的ROR原子方位关系概念邻域图更完整。

图5 本文所给概念邻域图与Rupam的比较Fig.5 ROR base relations’ conceptual neighborhood graphs given by Rupam(a)and us(b)

4 运动对象间方位关系推理方法

现有A、B、C三个对象,A、B间方位关系RAB和B、C间方位关系RBC已知,当A、C运动时,利用本文所提方法(DRA)可以求得A、C间的方位关系。DRA方法的步骤如下:

(1)当A、C未动时,根据ROR关系复合表求出A、C间可能的方位关系并保存在集合r中。

(2)当A、C运动时,根据ROR关系概念邻域图求集合r中每一个关系的邻域关系,得到的关系即为A、C间所有可能存在的方位关系。

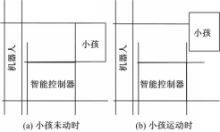
下面给出一个应用实例来说明DRA的有效性。现有智能家居中的3个对象,分别为机器人、智能控制器和需看护人员(这里为小孩)。已知小孩与智能控制器之间的方位关系为“FR”,智能控制器与机器人之间的方位关系为“R”,如图6(a)所示。小孩与机器人之间的方位关系未知。当小孩运动时,根据本文所提方法DRA,我们可以推断出小孩与机器人间可能的方位关系。根据这些可能的方位关系,机器人就可以找到小孩从而进行看护。首先,小孩未动时,根据表4,小孩与机器人间可能的方位关系为“FR,R,R&F”,即方位关系“FR”与“R”的复合结果。根据图5(a),“FR”的邻域关系有“F,OOR,R&F”,“R”的邻域关系有“OOR,OAL,R&B,R&F”,“R&F”的邻域关系有“FR,OOR,EOR,R”。由此可以推断出当小孩运动时, 小孩与机器人间可能的方位关系为“FR,R,R&F”三个方位关系概念邻域关系的并集,即“F,OOR,R&F,OAL,R&B,FR,EOR,R”。这样,机器人就可以根据这8种可能的方位关系找到小孩,从而执行看护等命令。图6所示为小孩运动时,小孩与机器人之间的方位关系由“R”(图6(a))变为“R&F”(图6(b))的情形。

图6 当小孩运动时,小孩与机器人间的方位关系由“R”变为“R&F”Fig.6 Transformation of orientation relation from “R” to “R&F” induced by motion

5 结束语

基于Rupam方位关系模型ROR,本文提出了ROR关系静态推理算法Composition,并给出了复合表;基于Freksa概念邻域结构[ 1],本文提出了一种ROR概念邻域关系自动生成算法AutoGen并构建了概念邻域图;将ROR关系复合表和概念邻域图与Rupam的进行比较,结果表明:本文不仅能够给出Rupam所给的正确结果,还能修正Rupam方位关系模型不存在的复合结果,且复合结果和概念邻域图更完整。最后,基于本文所给ROR关系复合表及概念邻域图,给出了运动对象间方位关系推理方法DRA的步骤,并用智能家居中的一个应用实例说明DRA方法的有效性。

The authors have declared that no competing interests exist.

参考文献
[1] Christian Freksa. Temporal reasoning based on semi-intervals[J]. Artificial Intelligence, 1992, 54: 199-227. [本文引用:4] [JCR: 2.194]
[2] Rand ell David A, Cui Zhan, Cohn Anthony G. A spatial logic based on regions and connection[C]∥Conf on Knowledge Representation and Reasoning, 1992: 165-176. [本文引用:1]
[3] Goyal R K. Similarity assessment for cardinal directions between extended spatial objects[D]. The University of Maine, 2000. [本文引用:1]
[4] De Weghe Nico Van, Cohn Anthony G, De Maeyer Philippe. A qualitative representation of trajectory pairs[C]∥ECAI, 2004: 1103-1104. [本文引用:1]
[5] Marco Ragni, Stefan Wölfl. Reasoning about topological and positional information in dynamic settings[C]∥Proceedings of the Twenty-First International FLAIRS Conference, 2008: 606-611. [本文引用:1]
[6] Rupam Baruah, Shyamanta M Hazarika. Modeling motion event using QSR[C]∥ECAI (Workshop), 2010: 61-66. [本文引用:2]
[7] 欧阳继红, 欧阳丹彤, 刘大有. 基于模糊集及RCC理论的区域移动模型[J]. 吉林大学学报: 工学版, 2007, 37(3): 591-594.
Ouyang Ji-hong, Ouyang Dan-tong, Liu Da-you. Region movement model based on fuzzy sets and RCC theory[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(3): 591-594. [本文引用:2] [CJCR: 0.701]
[8] Balbiani P, Condotta J F, Del Cerro L F. A model for reasoning about bidimensional temporal relations[C]∥Proc of the 6th International Conf on Principles of Knowledge Representation and Reasoning, 1998: 124-130. [本文引用:4]
[9] Allen J. Maintaining knowledge about temporal intervals[J]. Communications of the ACM, 1983, 26(1): 832-843. [本文引用:3] [JCR: 2.511]
[10] Balbiani P, Condotta J F, Del Cerro L F. A new tractable subclass of the rectangle algebra[C]∥In IJCAI-99, 1999: 442-447. [本文引用:2]