张耀娟(1981),女,博士研究生.研究方向:工程机械.E-mail:zhangyaojuan0714@163.com
经研究发现,解决履带车辆终传动破坏失效问题的关键在于该类车辆终传动与行走系统过盈接触问题。将过盈接触零部件看作刚性体,利用变形协调关系建立终传动和行走系统过盈接触问题的力学模型与数学模型,从理论上进行了研究。通过有限元仿真分析方法,以实车参数为依据,与理论模型进行互相验证,结果表明两者吻合较好,证明了本文方法的有效性。研究发现,终传动破坏的主要原因是终传动大齿圈轮毂的强度不足,安全系数仅为2.6,在恶劣工况时大齿圈轮毂的失效导致整个终传动的失效破坏。研究结果为履带车辆终传动的优化与改进提供了理论依据和计算方法。
The damage failure problem of the final drive of tracked vehicle was investigated. It was found that the interference contact between the final drive and the walking system is the key to solve the problem. First, the interference contact parts are taken as rigid bodies, and the mechanical model and mathematic model of the interference contact are established using the deformation compatibility relationship. Second, the finite element simulation method is employed to verify the proposed model using parameter of the practical vehicle. The finite element analysis results are in good agreement with that of proposed model, proving the effectiveness of the proposed method. Finally, it is found that the main reason of the final drive damage is the insufficient strength of the wheel hub of the large gear ring, whose factor of safety is only 2.6. This leads the failure of the wheel hub of the large gear ring under bad working condition, resulting in the failure damage of the final drive. This study provides theoretical basis for the optimization of the final drive of tracked vehicle.
过盈连接是利用过盈量使包容件和被包容件抱紧形成的一种连接,是机械部件常见的半永久型装配方式[
国内某公司的履带车辆[
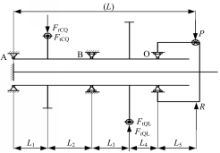
图1为履带车辆终传动第二级传动结构图,行走系统的行走架与终传动第二级传动结构右侧的行走架托座铰接,来自行走架上的载荷通过行走架托座既向终传动大齿圈轮毂传递,同时又向终传动半轴传递,传递过程中还经由了多个零件,传递关系错综复杂。此时来自行走架上的载荷在终传动大齿圈轮毂和半轴之间的载荷分配问题很难确定,导致大齿圈轮毂和半轴上承受的载荷无法确定,直接影响了它们的强度和刚度校核,从而无法从根本上解决终传动破坏失效问题。对于该问题,通过本文的分析研究发现,其实质是多零件过盈接触问题,需要综合运用弹性力学接触理论和结构力学超静定[
通过分析图1以及尺寸链分析可以发现,从履带车辆行走架托座到大齿圈轮毂的传递载荷路线, 以及行走架托座到终传动半轴的传递载荷路
线中,零件与零件之间的接触都属于过盈配合,在微小变形忽略不计的前提下,可以将中间传递载荷零部件看成是一体的刚性体。并且,由于行走架托座到终传动半轴的传递载荷路线中的刚性体与半轴是成一定锥度的过盈配合,因此可将此刚性体与半轴看成是固结一体的。由于行走架托座到大齿圈轮毂的传递载荷路线也构成过盈接触刚性体,因此整个结构就构成互相牵制,变形需要保持一致的整体,并且由于大齿圈轮毂与右端滚动轴承也是过盈配合,右端滚动轴承与整个刚性体也是过盈配合,因此终传动大齿圈轮毂与半轴之间就需要满足一定的变形协调关系,此时将弹性力学范畴的实体超静定结构归结成结构力学范畴的二力杆系超静定钢架结构,综合利用弹性力学、结构力学和材料力学的知识加以解决。由于终传动半轴左端以很高的压力压入机体,因此可将其左端看作是固定端,结合以上分析以及实际受力状况,抽象出的力学分析简化模型如图2所示:
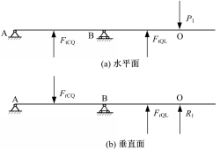
在图2中, FtCQ为大齿圈圆周力, FrCQ为大齿圈径向力, FtQL为驱动链轮圆周力, FrQL为驱动链轮径向力, 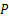
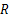
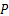
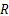
计算超静定结构的两个基本方法是力法和位移法。本文采用位移法的理念解决过盈接触实体超静定结构归纳出的二力杆系超静定钢架结构问题,该问题的关键是找出相互关联的变形协调条件。通过研究发现,该终传动与行走系统过盈接触超静定结构的变形协调条件为大齿圈轮毂和半轴的变形在相应位置上保持一致,这是解决该问题的突破口。
(1)取大齿圈轮毂为研究对象
大齿圈轮毂所受载荷分布在水平和垂直两个平面内,假设行走架在水平面内的载荷 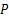
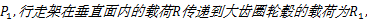
(2)取半轴为研究对象
半轴在水平面内的受力分析计算简图如图4所示:
由前文的分析已得出,该二力杆系超静定问题的变形协调条件为大齿圈轮毂和半轴的变形在相应位置上保持一致,则大齿圈轮毂与半轴在同一工况(本文选取满载工况)下在同一位置(本文选取O点所在截面位置)的位移(挠度)相等,因此变形协调条件为
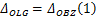
式中: 
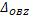
式(1)表示在满载工况下大齿圈轮毂和半轴在O点的位移相等,由于载荷分别在水平和垂直两个平面内,则水平和垂直平面内的变形协调方程分别为
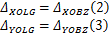
根据材料力学中的能量法可知,计算杆件变形结构位移的方法有单位载荷法,也称莫尔定理或莫尔积分,即
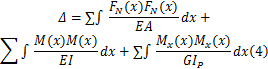
式中: 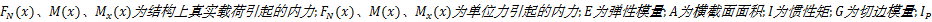
对于只受弯矩作用的杆件,计算位移的单位载荷法可写为
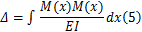
式中: 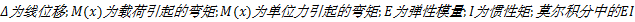
由数学知识可知,在 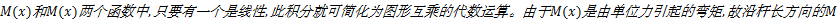
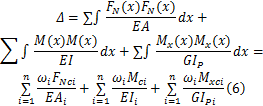
对于只受弯矩作用的杆件,计算位移的图乘法可写为
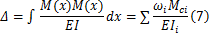
式中: 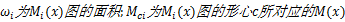
为计算方便,有时根据弯矩可以叠加的原理可将弯矩图分成几部分,对每一部分使用图乘法,然后求其总和。如果是几个载荷作用,可分别作出每一个载荷引起的弯矩图,然后利用图乘法和叠加法求其总和。本文就是利用图乘法和叠加法计算大齿圈轮毂和半轴的位移,然后根据变形协调条件,列出变形协调方程,计算出在满载工况下大齿圈轮毂和半轴在O点分别承受的载荷,从而推导出行走架上的载荷究竟是以怎样的分配比例向大齿圈轮毂和半轴传递的。
(1)根据水平面内的变形协调方程,求解出水平面内的载荷
①计算大齿圈轮毂水平面内O点的位移
根据图乘法和叠加法,大齿圈轮毂水平面内O点位移的计算公式可推导为
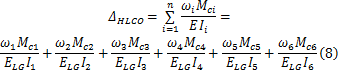
根据大齿圈轮毂在水平面内的受力分析简图,分别作出每一个载荷引起的弯矩图 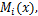
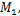
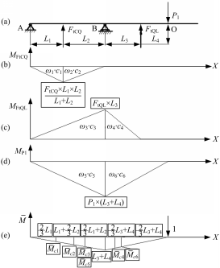 | 图5 大齿圈轮毂莫尔积分图乘法计算图Fig.5 Moore integral graph multiplication calculation chart of large gear ring wheel hub |
由图5和式(8)可计算出大齿圈轮毂水平面内O点的位移为
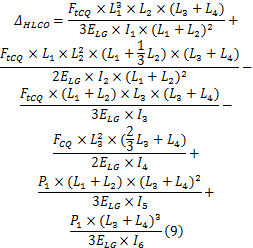
②计算半轴水平面内O点的位移
同理,利用莫尔积分图乘法和叠加法计算半轴水平面内O点的位移为
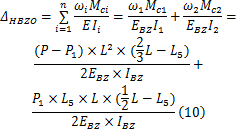
③列水平面内的变形协调方程
将大齿圈轮毂与半轴在O点的位移关系式(9)(10)代入到水平面内变形协调方程(2)中,得到
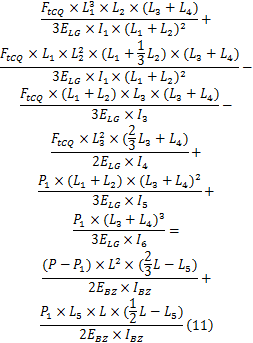
推导得出行走架在水平面内的载荷 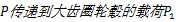
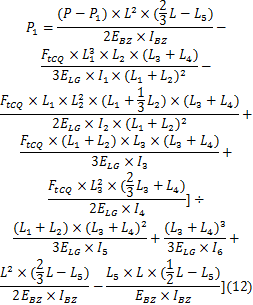
行走架在水平面内的载荷 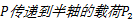

同理,在垂直面内,利用大齿圈轮毂与半轴在O点变形相等的变形协调关系,以及莫尔积分图乘法和叠加法,即可求解出行走架在垂直面内的载荷 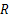
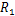
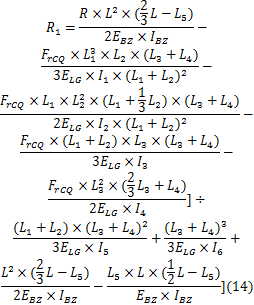
行走架在垂直面内的载荷 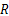
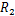

行走架传递到大齿圈轮毂的合成载荷 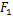
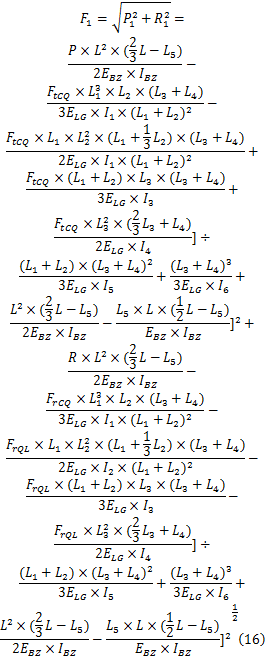
行走架传递到半轴的合成载荷 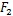
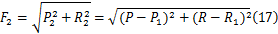
行走架传递到大齿圈轮毂和半轴的载荷确定后,就可以根据大齿圈轮毂和半轴的力学分析模型进行强度校核计算。大齿圈轮毂危险截面(即驱动链轮处)的强度为
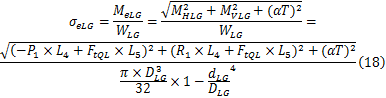
式中: 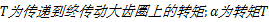
半轴危险截面(即半轴固定端处)的强度为
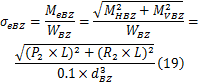
式中: dBZ为半轴危险截面(即半轴固定端)直径。
3.1.1 基本概况
履带车辆与本文计算相关的载荷参数中 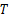
履带车辆长度尺寸参数如下: L1=71.0 mm, L2=124.0 mm, L3=160.3 mm, L4=86.3 mm, L5=59.8 mm, L=501.4 mm。
履带车辆直径尺寸参数如下: dLG=105.4 mm, DLG=439.7 mm, dBZ=106.0 mm。
大齿圈轮毂材料为45Mn,经查手册知其弹性模量 EG为206 GPa;半轴的材料为42GrMo,经查手册知其弹性模量 EZ亦为206 GPa。
3.1.2 理论计算结果
将履带车辆与本文计算相关的参数分别代入到行走架传递到大齿圈轮毂的合成载荷计算式(16)以及行走架传递到半轴的合成载荷计算式(17)中,经过运算得到终传动与行走系统过盈接触问题载荷的计算结果如下: P1=59 246.4 N, P2=-9 285.8 N, R1=15 898.1 N, R2=-2895.0 N, F1=61 342.3 N, F=9726.6 N。
将过盈接触问题载荷的计算结果代入到大齿圈轮毂和半轴的强度计算式(18)(19)中,进行强度校核计算,以便与有限元计算结果进行对比。大齿圈轮毂和半轴的强度校核计算结果如下:大齿圈轮毂危险截面处的应力 σeLG=145.5 MPa,半轴危险截面处的应力 σeBZ=40.9 MPa。
大齿圈轮毂材料为45Mn,经查手册知其屈服强度 σs为375 MPa;半轴的材料为42GrMo,经查手册知其屈服强度 σs为930 MPa。则在直线推土工况,大齿圈轮毂的安全系数为2.6,半轴的安全系数为22.7。在一般情况下,工程机械材料的安全系数为7~12,因此大齿圈轮毂材料的安全系数太低,在恶劣工况下容易发生破坏,需要采用力学性能更高的材料或是在结构上加以改进。由以上分析结果可知,终传动发生失效破坏最可能的诱因就是大齿圈轮毂的强度不足,因此需要对大齿圈轮毂进行改进设计;而半轴的安全系数又偏高,导致成本增加,从经济性方面进行考虑,半轴可采用力学性能稍低一些的材料。
本文采用Pro/Mechanica分析模块进行有限元仿真与理论分析进行互相验证。有限元仿真分析大体思路是利用厂方提供的行走及终传动原始设计模型,处理为Pro/Mechanica中可以识别的实体、壳等模型,按照给定的计算载荷组合批量计算。
3.2.1 有限元分析模型的简化及网格划分
在标准模块中建立简化几何模型,结构主体采用实体单元和板壳单元分析,网格采用自动网格划分和关键位置手工调节网格密度的形式。
3.2.2 有限元分析模型载荷及约束的施加
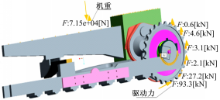
对于履带车辆直线推土作业工况,在整车重心处施加7.15 kN竖直向下的总载荷,在与履带板履齿接触的驱动链轮轮齿的分度圆上分别施加93.3、27.2、2.1、3.1、4.6、0.6 kN垂直齿面向上的圆周力,有限元分析模型载荷示意图如图6所示:
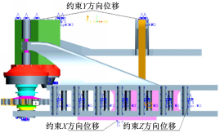
在行走架与顶推梁铰接处约束车体前进方向位移 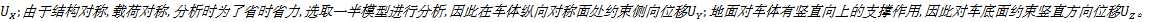
3.2.3 有限元仿真分析
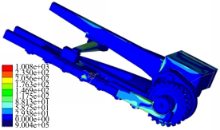
对履带车辆行走及终传动直线推土工况的整车进行有限元仿真分析,结果如图8所示:
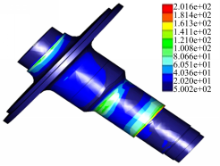
槛值为0~235 MPa。在履带车辆直线推土作业工况中,去掉因结构截面突变引起的局部应力集中,通过查看图9所示:
的大齿圈轮毂大应力区域分布图发现,大齿圈轮毂最大应力出现在与驱动链轮轮毂连接处,最大值为143 MPa,小于屈服极限375 MPa。通过查看图10所示:
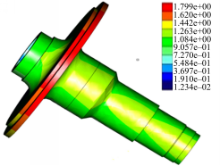
的大齿圈轮毂大位移区域分布图发现,大齿圈轮毂最大位移出现在大齿圈轮毂位于支承座一侧的端部,最大值为1.1 mm。在履带车辆直线推土作业工况中,通过查看图11所示:
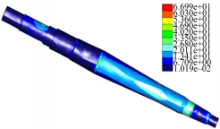
的半轴大应力区域分布图发现,半轴最大应力出现在半轴压入机体附近,最大值为39.2 MPa,远小于屈服极限930 MPa。通过查看图12所示:
的半轴大位移区域分布图发现,半轴最大位移出现在半轴与行走架连接的端部,最大值为1.0 mm。
行走及终传动的过盈接触问题难以用仪器进行测量验证,因此本文从理论计算与有限元仿真分析进行互相验证。大齿圈轮毂和半轴的强度校核理论计算与有限元仿真分析结果如下:大齿圈轮毂理论计算应力 σeLG=145.5 MPa,大齿圈轮毂有限元仿真应力 σeLG=143 MPa;半轴理论计算应力 σeBZ=40.9 MPa,半轴有限元仿真应力 σeBZ=39.2 MPa。
通过比较可知,大齿圈轮毂强度校核理论计算结果与有限元仿真分析结果误差为1.7%;半轴的强度校核理论计算结果与有限元仿真结果误差为4.3%。其误差均在5%以内,可以接受,证明行走及终传动过盈接触问题理论分析、力学模型和数学模型是正确的,且有限元仿真分析模型的简化、加载和计算也是正确的。因此,行走及终传动过盈接触问题理论分析方法和有限元仿真分析方法可以应用于此类问题中,为行走及终传动过盈接触问题的解决提供了两种切实可行的方法。从履带车辆行走及终传动过盈接触问题的计算结果(即大齿圈轮毂和半轴危险截面处的应力值)可以看出,大齿圈轮毂安全系数过低,在恶劣工况下容易发生失效,引起整个终传动系统的破坏,因此需要提高大齿圈轮毂的强度,以避免终传动的失效。将此信息反馈给厂家,经过对大齿圈轮毂在材料和热处理工艺方面的改进和加强后的终传动如图13所示:
改进设计后的5台履带车辆在制造基地的试验场地进行各典型工况和危险工况试验,如图14所示:
 | 图14 改进后实车各典型工况和危险工况试验Fig.14 The improved tracked vehicle tested in various typical and dangerous conditions |
试验结果表明,改进设计后的车辆在各工况下工作都是安全的,表明改进后终传动的强度和刚度都满足设计要求,说明本文的理论计算方法和有限元分析方法均是合理的,对辅助产品设计和开发有重要的指导意义,达到了设计合理化,缩短产品开发周期的目的。
通过以上的有限元仿真分析和理论计算公式(12)~(17)可知,履带车辆终传动与行走系统关键零件大齿圈轮毂与半轴的载荷分配主要与二者的刚度大小相关,进行产品设计时,从传递载荷机制角度考虑问题来设计结构零部件的刚度,运用本文中提出的数学模型以及有限元分析模型反复修改、计算,以进行优化设计,使零部件受力分配合理,最终达到履带车辆终传动与行走系统结构的优化设计。
(1)履带车辆终传动与行走系统过盈接触问题的分析方法可以为过盈接触问题的解决提供参考,即将错综复杂的各个过盈接触的零部件看作是一个整体,以便从整体上进行载荷的分配与力学分析。
(2)利用本文提出的过盈接触问题的分析方法,建立了履带车辆终传动与行走系统过盈接触问题的力学模型和数学模型,并采用有限元仿真分析方法与数学模型进行了互相验证,为工程车辆终传动与行走系统过盈接触问题的解决提供了可靠的理论计算方法和有限元仿真分析方法。
(3)通过分析发现,终传动与行走系统关键零件大齿圈轮毂与半轴的载荷分配主要与二者的刚度大小相关,从而进行产品设计时,应从传递载荷机制角度考虑问题来设计结构零部件的刚度,使其受力分配合理。
(4)计算出了终传动大齿圈轮毂和半轴各自分配的载荷,进而进行了强度校核计算,发现大齿圈轮毂的强度不足,安全系数仅为2.6,需要进行加强,将此结果反馈给厂家,改进设计后的5台履带车辆在制造基地的试验场地进行了各典型工况和危险工况试验。试验结果表明,改进后的履带车辆在各工况下工作都是安全的,很好地解决了工程实际中遇到的问题。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|