杨兆军(1956),男,教授,博士生导师.研究方向:数控装备可靠性理论.E-mail:yzj@jlu.edu.cn
为了分析和模拟伺服刀架可靠性试验台电液伺服加载系统的动态性能,建立了该加载系统的动态特性数学模型,并利用最小二乘算法对其参数进行估计。为了减弱噪声对加载系统稳定性的影响和避免无色卡尔曼滤波算法(UKF)中协方差矩阵出现病态导致算法失效,提出了利用基于奇异分解的无色卡尔曼滤波算法(SVDUKF算法)对电液伺服加载系统反馈力信号进行滤波的方法,并进行了SVDUKF算法与扩展卡尔曼滤波算法(EKF)算法之间滤波性能对比。实验结果表明,最小二乘算法估计出的数学模型具有较高精度,并且SVDUKF算法具有高效的滤波能力和提高系统稳定性的能力。
In order to analyze and simulate the dynamic characteristics of the electro-hydraulic servo loading system of the servo turret reliability test bench, a dynamic characteristics model of the electro-hydraulic servo loading system was established. The parameters of the dynamic model were estimated by the least square algorithm. For avoiding the system from the noise and preventing the Unscented Kalman Filter (UKF) algorithm from the ill-conditioned covariance matrix, a SVDUKF algorithm was proposed to smooth the force feedback signal of the hydraulic servo loading system. The filtering performances of the SVDUKF algorithm and the EKF algorithm were compared by experiments. The results show that the dynamic model with parameters estimated by the least squares algorithm has high precision; and the filtering performance of the SVDUKF algorithm has high-efficiency, which can improve the stability of the system.
为了使数控机床关键功能部件可靠性试验系统具有真实工况的模拟能力,加载系统需具有良好的动态性能和稳定性,因此需提高加载系统的参数估计和滤波能力。李福义等[ 1]综合考虑电液伺服阀、液压缸性能,给出的电液伺服阀和单出杆液压缸数学模型具有较高的精度。Lee等[ 2]提出的扩展卡尔曼滤波算法(EKF)能够从一系列不完全包含噪声的测量中估计动态系统的状态,具有较高精度;但是EKF的实质是对数学模型进行线性化,导致滤波后的值有较大误差,同时EKF处理高维的复杂模型时比较复杂。Wan等[ 3]提出的用于估计系统状态的无色卡尔曼滤波算法(UKF)在EKF滤波原理的基础上采用了UT变换,通过UT变换使非线性系统方程适用于线性假设下标准的Kalman体系,很好地克服了EKF的缺陷;但是试验中存在的干扰使协方差矩阵常为病态的,导致算法失效。Detiĉek等[ 4]提出利用最小二乘算法估计液压加载系统参数的方法,实现对液压加载力的精确控制。
本文根据电液伺服加载系统的动态特性,建立该系统的动态特性离散数学模型,同时利用最小二乘算法对数学模型中的参数进行在线估计。在此基础上,本文利用SVDUKF算法对电液伺服加载系统的反馈力信号进行滤波,以减弱噪声对加载系统稳定性的影响。SVDUKF算法采取用SVD代替Chol分解,解决了UKF算法存在的问题。
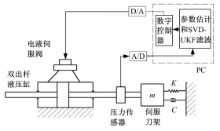
如图1所示:
1 数学模型建立及其参数辨识伺服刀架可靠性试验台主要由电液伺服阀1、双出杆液压缸2、拉压力传感器3、伺服刀架4、液压缸支架5和计算机控制系统等组成。电液伺服加载系统结构如图2所示:
根据电液伺服阀结构特点和动态特性可知,电液伺服阀阀芯位移与电流信号之间的关系如下[ 1]:
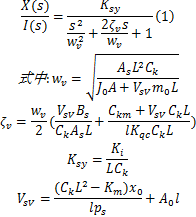
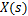
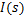
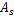
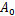
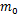
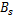
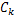
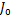
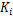
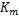
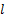
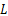
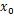
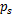
液压缸两腔的工作面积相等,因此两腔体的压差即为负载压力 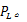
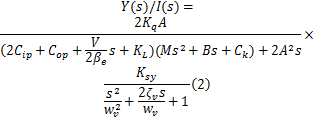
式中: 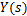
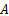
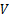
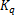
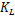
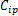
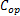
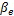
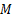
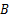
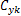
伺服刀架的力学模型如图2所示,其力平衡方程为
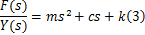
式中: 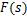
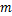
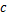
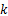
将式(2)乘以式(3),得出伺服刀架可靠性试验台电液伺服加载系统的动态特性数学模型为
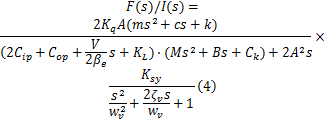
为了能更好地在计算机里表征加载系统的数学模型,本文对式(4)进行离散化处理(Z变换),得出加载系统离散数学模型为
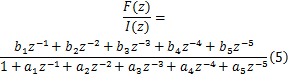
式中: 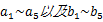
由于伺服刀架可靠性试验台受材料性能、结构、泵站等因素影响,式(5)中各参数时变,并且其变化规律具有不可预知性。为了能在线估计离散数学模型中各参数的数值,本文引入最小二乘算法。最小二乘算法在一定条件下有最佳的统计特性,即估计的结果是无偏的、一致并有效的,估计出的参数使数学模型在最小方差意义上与试验数据能很好地拟合。
由式(5)可得出电液伺服加载系统在 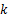
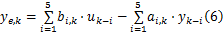
式(6)可变成如下形式:
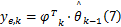
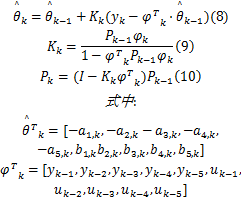
式中: 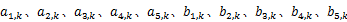
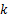
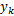
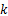
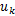
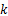
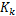
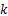
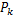
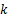
由于环境影响,计算机输出的控制信号和拉压传感器反馈信号中含有噪声,并且这部分噪声会降低加载系统的稳定性。当采用UKF滤波算法处理信号时,系统状态变量的协方差矩阵受噪声影响,易变成病态矩阵,导致UKF算法无法对协方差矩阵进行Chol分解,使算法失效。针对上述问题,本文引入SVDUKF算法,SVDUKF算法采用SVD分解代替Chol分解[ 8, 9],很好地解决了上述问题,提高了滤波器和加载系统的稳定性。
将上述加载系统的离散数学模型写成状态方程如下:
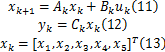
式中: 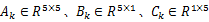
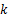
综上,SVDUKF算法可用于处理加载系统反馈的力信号,同时估计液压加载系统的状态。根据文献[8-12],SVDUKF算法可以描述如下:
(1)系统初始化
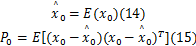
权值定义如下:
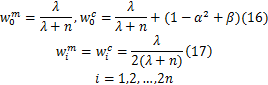
式中: 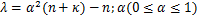
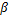
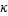
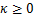
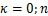
(2)计算sigma点
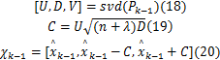
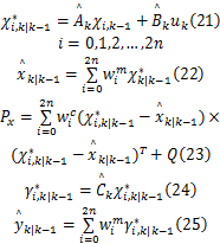
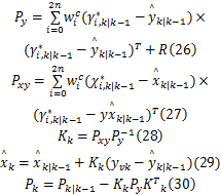
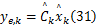
式中: 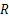
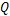
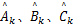
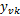
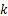
参数估计实验系统如图2所示,伺服阀采用MOOG/G761。计算机通过压力传感器和数据采集卡采集伺服刀架的力信号。在实验过程中,伺服刀架承受0.21 kN的静态力、0.06 kN的正弦动态力,数据采集卡的采样频率为250 kHz。
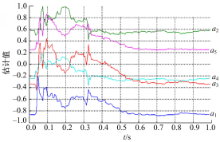
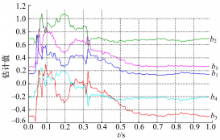
利用最小二乘算法对伺服刀架可靠性试验台电液伺服加载系统动态特性离散数学模型的参数进行估计。各参数的估计值如图3、图4所示:
从曲线的变化可知,各参数的值刚开始处于调整期,数据波动比较大,但是0.6 s以后各参数收敛到一个稳定值。各参数的估计值如下:
a1 =-0 .8563, a2 =0 .5752, a3=-0.3405,
a4 =-0 .2439, a5 =0 .2444, b1=0.1478,
b2 =0 .6946, b3 =-0 .5003, b4=-0.2057,
b5=0.2602。
参数估计过程中的相对误差如图5所示,相对误差计算式为
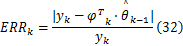
SVDUKF算法实验系统原理如图2所示。在实验过程中,伺服刀架承受0.21 kN的静态力、0.06 kN的正弦动态力,数据采集卡的采样频率为250 kHz。同时,SVDUKF算法对采集回来的信号进行在线滤波,并将滤波后的信号传送给控制器。为了提高SVDUKF算法的滤波性能,本文令状态变量 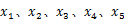
由于在滤波过程中各状态变量的变化相近,本文仅对状态变量 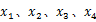
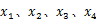
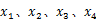
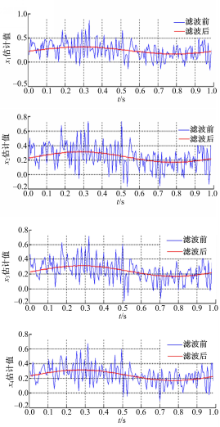
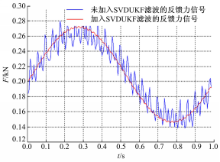
实验系统未加入SVDUKF滤波的反馈力信号(实际反馈力信号)与加入SVDUKF滤波后的反馈力信号的对比如图7所示:
从图7可知,实验系统实际反馈的力信号波动较大,当引入SVDUKF滤波算法后,信号曲线比较平稳。通过计算,加入SVDUKF滤波算法前、后信号中噪声的均方差分别为0.7662和0.00051。因此SVDUKF滤波算法能减弱噪声,降低噪声对系统稳定性的影响。
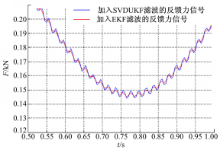
EKF算法和SVDUKF算法在相同初值条件下,对反馈力信号处理部分结果如图8所示:
从图8可知,SVDUKF算法滤波后的力信号比EKF算法滤波后的力信号更平稳。通过计算,用EKF算法过滤后的信号中,噪声的均方差为0.0012。综上,SVDUKF算法相对EKF算法更能维持加载系统稳定性,因此经过SVDUKF算法滤波后的信号是加载系统最终需要的信号。
(1)根据电液伺服加载系统的动态特性,建立了该系统的动态特性离散数学模型,同时利用最小二乘算法对数学模型中的参数进行估计。实验结果表明,最小二乘算法估计的参数很快地收敛到各自稳定值附近,并且得出的数学模型具有较高的精度。
(2)用SVDUKF算法对电液伺服加载系统反馈的力信号进行滤波,并与EKF算法进行了滤波性能对比实验,结果表明,SVDUKF算法的滤波性能优于EKF算法,并且更能提高加载系统的稳定性。
(3)由于SVDUKF算法比较依赖于数学模型的精度,因此后期工作的重点是建立更为精确的电液伺服加载系统动态特性数学模型和研究提高最小二乘算法参数估计精度的方法。
| [1] |
|
| [2] |
|
| [3] |
|
| 4 |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|