李娟(1970),女,副教授,博士.研究方向:信号与信息处理.E-mail:ljuan@jlu.edu.cn
为了减少传统的DV-Hop算法对未知节点定位时产生的较大误差,分析了影响传统DV-Hop算法定位精度的两个因素,继而提出了一种改进算法。改进算法在进行未知节点定位时,信标节点先后使用两个通信半径广播自身位置信息,从而获得未知节点与信标节点间更精确的跳数,并计算出它们之间更精确的距离,得到未知节点更精确的坐标。仿真结果显示,改进算法相比于传统DV-Hop算法相对定位误差减少了13%~15%,并且减少了由于网络拓扑结构不同带来的定位误差的差异性。
Traditional DV-Hop algorithm can cause greater positioning errors. To overcome such problem, the traditional DV-Hop algorithm was analyzed and simulated, and two factors affecting positioning accurate were acquired. Then an improved positioning algorithm was proposed. Two communication ranges were used by beacon during localization. Using this method more accurate hops between beacon and unknown node can be gotten and the estimating distances between beacon and unknown node are close to real distances. Numerous simulation results show that the relative positioning error of the improved algorithm is 13% to 15% less than that of traditional DV-Hop algorithm. Moreover, the differences of positioning errors in different network topologies are decreased by using this improved algorithm.
对网络中未知节点定位是无线传感器网络的关键技术之一[ 1]。对目前提出的定位方法,依据定位时是否用到角度和距离,可分为基于测距和无需测距的定位算法。由于节点尺寸、消耗和能量的限制,无需测距的定位方式有较强的实用性[ 2, 3]。DV-Hop[ 4]定位算法属于无需测距的定位算法,在低信标点密度的情况下也能获得较高的定位比例,但是由于利用跳段距离代替节点间距离,定位精度受到网络拓扑结构的影响,有些节点定位误差较大。在DV-Hop算法的基础上,陆续出现了多种改进算法。文献[5]提出的人工布设信标节点的DV-Hop改进算法,在一定程度上提高了定位精度,同时具有较强的稳定性,不足之处是人工布置方式有时难以实现。文献[6]提出的信标节点反馈的DV-Hop算法与传统的DV-Hop算法相比几乎不能提高定位精度。文献[7]提出了一种基于加权的平均每跳跳距的DV-Hop算法,未知节点对各个信标节点估计的平均跳跳距进行归一化加权处理,赋予离未知节点近的信标节点大的权值。文献[8]的平均每跳跳距误差修正的DV-Hop算法,在分析每个信标节点的平均每跳跳距误差后,进一步修正先前得到的网络的平均每跳跳距。文献[7]和文献[8]与传统DV-Hop算法相比定位精度有所提高,不足之处是通信和计算量开销比较大。文献[9]在平均每跳距离估计、未知节点到各参考节点之间距离的计算和节点位置估计方法3个方面进行了改进,却增加了节点的计算量。
为了提高DV-Hop算法的定位精度,本文提出一种基于双通信半径的DV-Hop算法。在进行定位的过程中,未知节点只使用一种通信半径 R,而信标节点先后使用两种通信半径 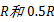
DV-Hop定位算法[ 10]通过洪泛模式,待定节点首先获得与信标节点的最小跳数。然后根据信标节点间的距离和跳数,可以估算出节点间的平均每跳跳距。最后利用未知节点到信标节点的最小跳数乘以平均每跳跳距,未知节点就可以得到与信标节点之间的估计距离。再利用三边测量法或极大似然估计法求解未知节点的坐标。
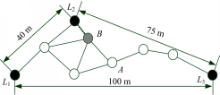
假设一个简单的网络如图1所示:
图中 
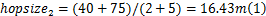
未知节点 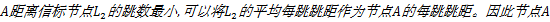
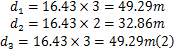
在洪泛的过程中,信标节点首先广播自身的位置信息,此时在信标节点通信范围内的节点都能够接收到广播信息,接收到信标广播的节点称为该信标节点的邻居节点,本文称之为信邻节点。信邻节点记录到信标节点的最小跳数,忽略来自同一个信标节点的较大跳数。然后将跳数值加1,并转发给其通信范围内的邻居节点。如此反复,信标节点的位置信息以及到信标节点的跳数信息在网络中传播开来。最终每个节点只保留到信标节点的最小跳数。在这个过程中通信范围(即节点的通信半径)是至关重要的因素,因为通信半径决定了哪些节点是上一级节点的邻居节点,也进一步决定了节点间的最小跳数,同样也决定了每跳距离。
为了研究通信半径与定位精度之间的关系,本文做了如下实验。在100 m×100 m的区域内随机布设100个节点,其中10%为信标节点,研究在不同通信半径下DV-Hop定位算法的定位误差。本文采用相对定位误差 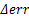
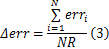
式中: 
通过100次的仿真实验得到的平均结果见表1:
| 表1 DV-Hop算法相对定位误差与通信半径的关系 Table 1 Relative localization errors of DV-Hop algorithm with difference communication ranges |
从表1中可以明显看出,随着通信半径的增大,相对定位误差逐渐减小。除通信半径外,另外一个重要的因素就是信邻节点。从信标节点发出的信息全部通过这些信邻节点传播出去,所以网络中其他节点到信标节点的跳数和跳距都与这些节点有关。
根据前文的分析,通信半径和信邻节点是DV-Hop定位算法中重要的两个因素。因此,如果能够得到信邻节点与信标节点相对更准确的距离,无疑能够提高所有未知节点的定位精度。本文考虑对每个信标节点引入两个通信半径,一个是与其他未知节点相同的全网通信半径 R,另一个是信标节点所独有的通信半径0.5 R。当信标节点以通信半径 R广播信息时,所有能够收到广播的邻居节点构成信邻节点组1;当信标节点以通信半径0.5 R进行广播时,收到广播的邻居节点构成信邻节点组2。显然,信邻节点组1包含信邻节点组2的所有节点。在广播过程中,信邻节点组2中的所有节点保留的与信标节点的最小跳数是0.5,信邻节点组1中除去信邻节点组2的其他节点保留与信标节点的最小跳数为1。在此基础上,信邻节点继续以通信半径 R洪泛的方式转发信标节点传来的信息。洪泛结束后,每个节点都保留到所有信标节点的最小跳数。其中,最短传播路径通过信邻节点组2的节点中保留的最小跳数不再是一个整数,而是一个整数加上0.5。显然,与只用一个通信半径 R的情况相比,这些节点的绝对定位误差就减小了0.5 R,从而使这些节点的定位精度有了明显提高。此外,信标节点采用多一个通信半径0.5 R也能够使跳距的计算更接近真实值,同样能达到提高定位精度的目的。
同样以图1的网络为例,信标节点 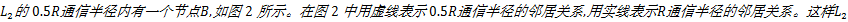
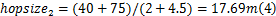
由式(4)计算得到的平均每跳跳距比式(1)的结果更接近真实值。未知节点 
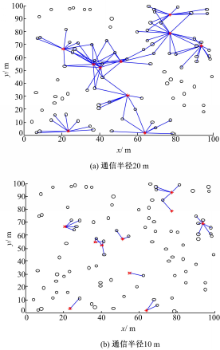
如果在100 m×100 m的区域内随机布设100个节点,其中10%为信标节点,当通信半径分别为20 m和10 m时,信标节点与信邻节点拓扑关系图如图3所示:
从图3(a)与图3(b)的对比来看,采用0.5倍通信半径后,信邻节点的数量约占原信邻节点数量的三分之一,这对整个网络中未知节点定位精度会有较大程度的影响,而且随着网络连通度的增加,这个比例还会增加,影响程度也会随之增加。
(1)未知节点获取到每个信标节点的最小跳数。
网络启动工作时,信标节点会主动广播自身位置信息的分组,信息中包括信标节点的坐标和初始化的跳数字段。另外,每个节点都会预留出足够的存储空间,用于保存与每个信标节点的最小跳数。网络初始化阶段,这些存储空间全部置0。当某个信标节点的信息首次传送到一个节点时,该节点将直接存储接收到的跳数字段;当这个信标节点的信息并非首次传送到该节点时,该节点比较本次接收的跳数字段与之前存储的与该信标的跳数系数后,存储二者较小的数值作为最小跳数。存储完成后,将最小跳数加1后赋值给传播信息的跳数字段,转发给邻居节点。这样,最后网络中的所有节点都能记录下到每一个信标节点的最小跳数。
本算法中,信标节点有两个通信半径,一个为的作用是确保第一次广播的信息被信邻节点接收到并完成更新最小跳数的操作。
每一次洪泛式传播节点都会消耗较大的通信能量。由于无线传感器节点能量受限,所以本算法只是第二次广播采用洪泛式传播,而第一次广播仅仅是信标节点发送信息给信邻节点,信邻节点并不继续广播。信标节点通常是特殊节点,存储的能量会远远大于其他节点,而多一次广播也不会增加很多的能量开销。
(2)计算未知节点与信标节点之间的距离。
每个信标节点依据存储的其他信标节点的坐标以及与它们之间的最小跳数估算平均每跳距离为
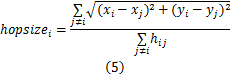
式中: 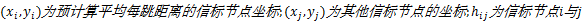
由于增加了以0.5 R为通信半径的第一次广播,这里的最小跳数可能是一个整数或者一个整数加上0.5。
信标节点以通信半径 R将平均每跳距离以洪泛的方式广播出去,每个未知节点仅记录第一次接收到的平均每跳距离,并转发给邻居节点。洪泛结束后,未知节点根据接收到的平均每跳距离以及先前记录得到各个信标节点的最小跳数计算到每个信标节点的跳距。
(3)每个未知节点利用极大似然法计算自身位置。
为了检验改进的算法的性能,本文对原DV-Hop算法和改进算法分别进行仿真,研究在不同通信半径和信标节点比例下两种定位算法的性能。由于DV-Hop定位算法受网络拓扑结构的影响较大,对于不同的网络结构,定位算法的精度会发生变化。因此,为了使仿真结果具有说服性,本文针对每种通信半径和信标节点比例情况分别进行了100次的网络仿真实验。每次实验都假设网络的区域大小为200 m×200 m,在这个正方形区域中随机布设400个节点,并且每一次实验都会重新布设节点,这样每一次实验网络都会具有不同的拓扑结构。经过100次实验后,取平均值作为仿真的结果。
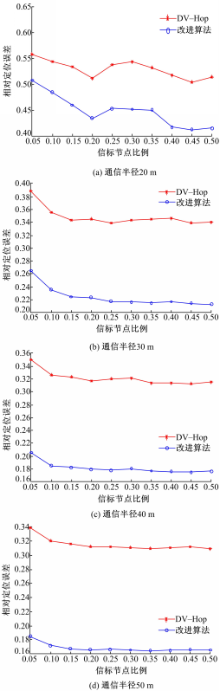
图4(a)~(d)分别为在不同通信半径的情况下,两种定位算法的相对定位误差与信标节点比例的关系图。在改进算法中通信半径是指两个通信半径中较大者。从图4中可以看出,在不同通信半径的情况下,改进算法的相对定位误差相对原算法有不同程度的减少。通信半径为30 m~50 m的情况下,定位效果稳定,相对定位误差减少了约13%~15%。
另外,从这4幅图中都可以看出相对定位误差随着信标节点比例的增加具有减小趋势。但是,当信标节点比例大于20%之后,趋于稳定,减小并不明显。因此,虽然信标节点的增加能够提高定位精度,但是使用DV-Hop或者改进算法定位时,没有必要采用过多的信标节点。当使用改进算法定位时,即使信标节点比例在5%的情况下,只要通信半径大于30 m,平均相对定位误差就会小于27%。
从这4幅图的对比中还可以看出,随着通信半径的增大,相对定位误差逐渐减小。由于在网络的节点总数和信标节点不变的情况下,增大通信半径相当于提高网络的连通度。连通度提高了,自然定位误差就会减少。
由于图4所示的结果为100次网络仿真实验的平均结果,为了了解不同网络分布情况对算法定位效果的影响,本文给出了信标节点比例为20%的情况下、在不同通信半径时,两种算法在100次网络仿真实验中得到的相对定位误差的最大值和最小值,见表2:
| 表2 两种算法相对定位误差的最大和最小值 Table 2 The max and min of relative localization error of DV-Hop algorithm and improved algorithm with different communication ranges |
从表中的数据可知,在完全相同的仿真条件下,网络结构不同时,定位算法误差的差异较大。DV-Hop算法最大值与最小值相差10%~18%,改进算法相差4%~11%。改进算法的差异相对小一些。
在DV-Hop算法基础上提出了一种改进算法。从仿真结果可以看出,在不同通信半径和信标节点比例下,改进算法的相对定位误差相对原定位算法减少了13%~15%。另外,在相同仿真条件下,由于网络拓扑结构不同会带来定位误差的差异性。改进算法在提高精度的同时减少了该差异的大小。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|