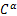
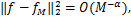
图像中的边缘,纹理等几何结构在一定方向上均存在正则性,比如图像在平行于物体边缘的方向上可微。对于正则化程度越大的信号,其在最优小波基下的逼近误差越小,即图像的大部分信息集中在更少的系数中。大多数多尺度变换对图像几何结构缺乏先验知识,使用预先固定的基(或框架)来分析图像,没有有效地利用图像各项异性的正则性,因此无法较稀疏地描述图像中的几何特征。

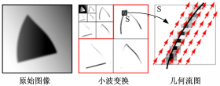
第二代Bandelet变换是一种新的多尺度变换,其核心思想是为图像中的几何特征定义矢量场(几何流),矢量所指示的方向即为该位置处几何特征的正则化方向,将小波域系数分割为各个子块,每一子块对应了一个固定的几何流,进一步对块中数据“Bandelet化”来获取最优的非线性逼近能力。Bandelet基函数与各子块中的几何流相对应,具有自适应性,因此能更有效地刻画图像中的方向性特征。图1显示了在图像小波域中某子块S的几何流,图中的箭头代表该点的几何流。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 图像的局部几何流Fig.1 Local geometrical flows for the image

第二代Bandelet变换的主要步骤如下:

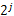
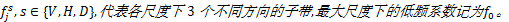
(1)对图像进行二维离散小波变换,得到尺度 下的子带系数图像

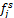
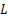
(2)将 循环分割为大小相等的4个子块,在每一次循环得到的各子块中重复步骤(3)~(7),直到最终得到子块S的宽度 达到某预设值,一般取这个值为4或8个像素。

(3)在各子块S中按离散的网格格点与子块中心的位置关系确定各种可能的正则化方向,其总数应小于 重复后面的步骤(4)(5)。

(4)将块S中的数据进行正交方向(垂直于几何流)的投影,按投影数据的位置顺序对原数据从左至右排列后得到一维数据

(5)对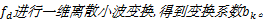

(6)设定阈值 作为块S中几何流所指示的方向。该步骤首先计算各方向下

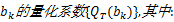
然后选择最优的几何方向,使得式(2)所示的Lagrangian函数取得最小值:

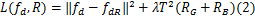
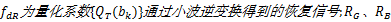
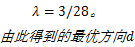
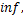
式中: 分别为对块S中几何流、量化系数编码所需要的比特数; 即是块S中图像几何结构的正则化方向。对于无几何流情况,将该子块方向标记为 且不对该块中原始的小波系数做任何处理。

(7)将最优几何方向 按“Z”字型排列为二维矩阵形式,确保低频系数处于矩阵的左上角。

(8)根据Lagrangian函数最小化原则,借助分类和回归树模型,自底向上地合并各子块,从而建立最优的四叉树结构。叶子节点对应了最终Bandelet子块,子块中的系数 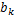即为Bandelet变换系数。

第二代Bandelet变换步骤(1)中使用的小波变换为非冗余的正交(双正交)小波变换,该变换不能有效地捕获图像的某些细节信息,而且由于缺乏平移不变性,容易在图像奇异处产生伪Gibbs效应。本文因此使用非下采样的小波变换(NSWT)^{[ 5]}:

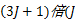
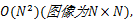
该变换是一种冗余的图像表达方式,提供的系数数据为原始图像数据的 为二维变换的尺度总数)。由此造成的数据冗余势必增加算法的计算量,为了提高算法的运算速度,在计算几何流时,取消计算最优四叉树的步骤,避免了逐级归并和计算几何流的操作,在固定大小的分块中计算几何流,计算复杂度仅为 比原来的Bandelet变换缩小了(log₂ N)²倍^{[ 6]},较大地减少了计算量。

非下采样的Bandelet变换(NSBT)是第二代Bandelet变换的改进形式,它取消了原变换中二维小波变换所涉及的下采样过程,因此具有一定的数据冗余,进而可以为融合过程提供更丰富的源信息,并且该变换具有平移不变性,可以有效减少因源图像误配准对融合过程造成的影响。

基于非自适应变换的融合方法是将源图像通过一组固定的基进行表示,对得到的变换系数按照一定的规则进行融合处理,最后再通过这组基对融合系数重建得到融合图像,该过程中源图像对应的变换系数是通过同一组基投影得到的,因此对系数的各种融合操作具有合理性。而Bandelet变换是一种自适应的变换,由于源图像之间的几何结构存在差异,对应Bandelet子块中小波系数的正则化方向也不可能相同,由此得到的图像基函数是不一致的,导致建立在不同基函数上的Bandelet系数之间不具有可比较性,对其进行各种融合运算缺乏合理的依据,因此常见的融合框架不再适用于这类变换的融合,有必要使用一种新的方案。

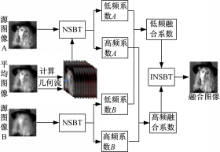
考虑到多聚焦图像,源图像之间具有一定的相似性,文本使用如图2所示的融合方案(以两幅源图像的融合为例),该方案主要包括以下步骤:

(1)计算待融合源图像的平均图像。

(2)利用所得图像计算各尺度下Bandelet子块中的几何流。

(3)该几何流对应了一组Bandelet基,利用这组基对源图像做非下采样Bandelet变换。

(4)将变换得到的低、高频系数分别按一定的融合规则进行选取。

(5)对得到的低频融合系数和高频融合系数进行非下采样Bandelet逆变换(INSBT);最终获得融合图像。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 融合方案Fig.2 Fusion scheme

由于该方案中得到的Bandelet系数是建立在相同的Bandelet基上的,因此对其进行相关的融合运算是合理的。

图像经NSBT分解后的低频系数代表了图像的近似分量,包含了大部分的能量信息;高频系数则代表了图像不同尺度下的细节信息,包括几何结构的正则化方向和正则化程度。考虑到各频带系数对应的物理意义不同,本文使用如下融合规则:

(1)低频融合系数。NSBT得到的低频系数可以看作是具有各项同性正则化的图像,因此没有进行任何“Bandelet化”操作,该系数也就是NSWT得到低频系数。本文使用各源图像低频系数的平均值作为最终的低频融合系数。设 处的低频系数,低频融合系数为

(2)高频融合系数。NSBT在NSWT产生的高频系数上进行了正则化方向的一维小波变换,得到的Bandelet系数分别包含了低频分量和高频分量,本文分开对其进行考虑。设 分别为子块S中的低频Bandelet系数和高频Bandelet系数,低频部分的融合方案如下:

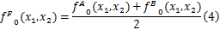
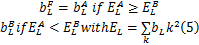
式中: 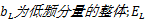为低频分量的总能量。

高频部分使用如下的融合方案:

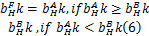
即选择绝对值较大的高频系数作为融合系数。

实验使用融合图像和残差图像作为实验效果的主观判据,残差图像通过参考图像与融合图像相减得到,图中残留的图像信息越少,说明融合图像与参考图像越接近,融合效果越好。为了便于观察,将残差图像的灰度值放大5倍显示。实验采用峰值信噪比(PSNR)、互信息(MI)^{[ 7]}、边缘保持度( Q^AB/F)^{[ 8]}作为融合性能的客观量化指标,它们分别定义如下:

(1)峰值信噪比(PSNR)的具体定义为

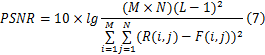
式中:R、F分别为参考图像和融合图像; 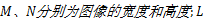为灰度级数。

峰值信噪比越高说明融合图像与参考图像越接近。

(2)互信息(MI)从统计学角度定义了两幅图像的相关性。源图像A和融合图像F的互信息为

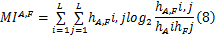
式中: 为图像A和F的归一化联合灰度直方图; 是两幅图像的归一化直方图。

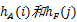
源图像B和融合图像F的互信息用MI^B,F表示。融合结果通过各源图像和融合图像互信息的和来评价,即MI=MI^A,F+MI^B,F。互信息值越大,表示融合图像从源图像提取的信息越多,融合的效果也越好。

(3)边缘保持度( Q^AB/F)的定义为

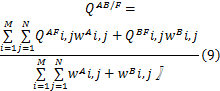
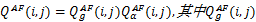
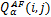
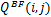
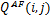
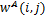
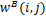
式中: 为边缘强度保持度, 为边缘方向保持度。

的定义与 类似。 和 是权重因子。 Q^AB/F的取值范围为[0,1],越靠近1,说明融合图像的边缘信息损失得越少,融合效果也越好。

图4分别显示了4组源图像的融合结果。从实验中可以看出,基于WT融合方法得到的残差图像各种特征较为明显;基于NSWT的融合方法得到的残差图像中出现的物体特征较少;基于NSBT融合方法的残差图像残留的信息最少,且轮廓细节比较均匀。造成以上现象的原因是WT方法得到的系数量不够冗余,融合结果对系数的融合规则比较敏感,容易受噪声和误配准影响。基于NSWT的融合效果有较大改善,但其对图像中的几何特征表示仍不够理想,在物体的边缘处仍有较多残差。NSBT融合方法以近似最优的形式表示图像,更集中地反映了图像的几何特征信息,降低了噪声等外来因素的影响,使随后的融合系数选取更加准确,因此图中残差较少且模糊。需要注意的是,WT融合方法的残差图像中物体的边缘均出现了明显的振荡条纹,这主要是因为各尺度下对应位置的融合系数的来源可能不一致,会在融合图像中产生伪Gibbs现象,而WT存在下采样操作,所造成的频率混叠会加剧这种效应。由于余下两种方法具有平移不变性质,这种现象明显地减小了。表1列出了各融合方法的量化评价数据。可以看出,基于WT的融合方法的量化结果最差,基于NSWT的融合方法的结果有较大改善,基于NSBT的融合方法的结果均优于其他融合方法,这也与从图4中获得的直观感受一致。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同融合方法的融合图像和残差图像Fig.4 Fused images and difference images using different fusion methods

表1

Table 1

表1(Table 1)

表1 不同融合方法的客观评价 Table 1 Objective assessment of different fusion methods 源图像 融合方法 量化指标 PSNR MI QAB/F Fig.3 (a) WT 33.3030 5.7813 0.6347 NSWT 35.7578 6.2666 0.6853 NSBT 38.0482 6.4659 0.7005 Fig.3 (b) WT 34.5479 6.9549 0.6858 NSWT 36.5783 7.4312 0.7262 NSBT 37.6580 7.5917 0.7345 Fig.3 (c) WT 37.7222 9.0428 0.6978 NSWT 41.7010 9.6970 0.7386 NSBT 42.3785 9.7280 0.7402 Fig.3 (d) WT 35.3033 4.9127 0.6679 NSWT 39.3839 5.5062 0.7199 NSBT 40.3054 5.5443 0.7276

表1 不同融合方法的客观评价 Table 1 Objective assessment of different fusion methods