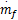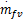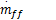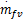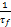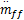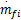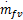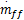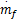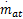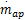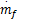石屹然(1984),男,博士研究生.研究方向:控制理论与控制工程.E-mail:35105767@qq.com
针对SI发动机空燃比(Air-fuel ratio, AFR)控制的问题,首先对标准Volterra模型进行了改进,提出了一种变采样间隔的多输入多输出Modified Volterra模型。并应用该模型实现了发动机AFR系统的在线自适应辨识。并在此基础上,提出了一种基于Modified Volterra模型的非线性模型预测控制方法。利用Matlab对一种业内普遍认可的基准发动机模型进行了仿真实验,并与当前汽车广泛使用的PI控制器算法进行了对比。仿真实验结果证明了本文方法的有效性。
The control of the Air-Fuel Ratio (AFR) for SI engines is investigated. First, the traditional Volterra model is improved, and a modified multi-input multi-output Volterra model with variable sampling intervals is proposed. This model is employed to achieve engine AFR adaptive modeling online. Then, on this basis, a nonlinear model predicting control method based on the modified Volterra model is developed. Finally, using Matlab, simulation of the proposed control model is carried out with a widely accepted SI engine benchmark, and compared with the currently used PI controller algorithm. The results show that the proposed method is effective.
三元催化器(Three-way catalyst,TWC)有效降低了发动机尾气中三大污染物质:NO x,CO,HC的排放。理论和实践均证明将发动机空燃比(Air-fuel ratio,AFR)准确地控制在14.7±1%的范围内,不仅能使TWC工作在最佳效率点,从而在最大程度上降低尾气污染物的排放,而且还使得发动机燃油效率以及整体性能得到极大提高[ 1, 2, 3, 4]。
目前,发动机AFR控制广泛采用的是查表加PI反馈补偿的方法[ 5, 6]。这种方法虽然简单可靠,但由于发动机具有很强的非线性,其控制效果并不理想[ 1, 2, 7]。Choi和Hendrick提出了一种基于状态观测器的AFR滑模控制方法[ 7]。该方法使得系统输出响应速度大幅度提升,同时也降低了系统输出的稳态误差。但当发动机性能或燃料特性改变时,控制效果急剧下降。针对此问题,Yoon和Sunwoo提出了一种自适应动态滑模控制的AFR控制方法,有效地解决了由于发动机性能或燃料特性改变时模型发生改变的问题[ 8]。近些年,随着非线性理论的飞速发展,非线性模型预测控制的理论与研究越来越受到学者们的关注。Manzie等人利用RBF神经网络对发动机进气量实现了多步预测,并取得了很准确的预测效果[ 1]。基于这个成果,Wang等[ 9]提出了基于RBF神经网络的发动机AFR非线性模型预测控制方法。该方法利用一种简化Hessian矩阵的SQP方法得到基于RBF神经网络的最优喷油量序列,实现了对AFR的非线性模型预测控制。在随后的一篇文章中,Wang等[ 10]又提出了一种基于MLP神经网络的发动机AFR控制方法,并取得了很好的控制效果。然而,由于神经网络是一个凹函数,使得该方法常常陷入局部最小值的困扰[ 11, 12]。并且,神经网络由于其本身的非参数化结构特点使得模型信息很难得以利用,这给后续最优控制算法的研究带来了很大困难。
为了解决这一问题,本文采用参数化的多输入多输出的Voletrra模型来描述SI发动机非线性模型。Volterra模型是Taylor模型的一个扩展,是非线性系统的一个通用数学表达形式,具有良好的收敛性。大量实践证明,仅需要较低的阶次(一般为二阶或三阶)就可以很好地逼近一大类非线性系统[ 13, 14, 15]。特别是它将系统的线性部分和非线性部分分开的表达方式使它既具有鲜明的物理意义又具有良好的操作性,在非线性系统分析与辨识中得到广泛的应用[ 13, 14, 15]。
SI发动机是一种多输入多输出系统,其发动机进气阀角度与喷油量的质量流速的过渡过程时间存在极大差异。为此,本文提出了一种变采样速率的修正Volterra级数的SI发动机辨识模型,该模型不仅降低了Volterra模型的截断阶次,而且还有效地提高了模型辨识精度。在此基础上,本文提出了一种基于Modified Volterra模型的SI发动机AFR模型预测的自适应滚动优化控制方法。该方法利用SI发动机的Modified Volterra模型对真实系统输出AFR进行多步预测,在AFR控制误差平方和最小的准则下,通过滚动优化的方法形成最优的控制序列。同时,利用Matlab对一种业内普遍认可的基准发动机模型,即平均值发动机模型[ 16](Mean value engine model,MVEM)进行了仿真实验,并且与当前汽车广泛使用的PI控制器算法进行了对比。仿真实验证明了本文方法的有效性。
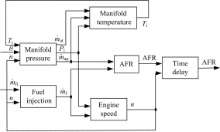
如图1所示:
MVEM模型被分成三个子模型以描述发动机进气管的压力和温度、转速以及喷油量的动态过程。该模型的两个系统输入分别为进气阀角度θ和喷油量质量流速 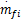
从空气质量守恒的角度分析进气管进气的动态过程,可以得出关于进气管压力以及进气管温度的非线性微分方程[ 16]
: 
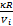
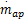
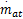

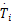
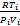
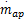
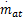
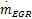
式中:P i为进气管压力;κ为空气的比热容;R为气体常数,本文取R=287×10-5、V i为进气管体积;T i为进气管温度;T a为环境温度; 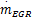

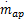
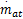

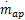
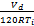
式中:
β1(v)=1- cos(v)- 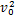
P r=P i/P a(6)
β2(Pr)=
 | (7) |
式中:m at0,m at1,v0,P c是定值;η i为容积率;η i·p i为归一化的压缩气体压强,可通过式(8)求得[ 16]:η i·p i=s i(n)P i+y i(n) (8)
式中:s i(n)和y i(n)为发动机转速的函数,并且y i(n)≪s i(n)。
基于曲轴的能量传动,转速的微分方程表示为
[ 16]
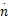 | (9) |
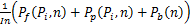

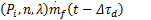
式中:摩擦功率P f和抽运功率P p与进气管压力P i和转速n密切相关;负载功率P b是转速n的函数;Δτ d为喷油的延时时间;容积率η i为进气管压力P i、转速n和空燃比AFR的函数,I为归一化处理后的发动机转动惯量;n为发动机转速。
Volterra模型作为Taylor模型的一种推广模型一经提出即引起了学者们的广泛关注。一般来讲,二阶Volterra模型即可很准确地描述一个非线性系统[ 13, 14, 15]。标准二阶Volterra MIMO模型的表达形式为
yi(k)=hi0+ 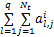
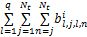
式中:Nt为截断阶数;q为输入变量个数;i为系统输出个数; 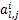
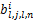
发动机系统输出AFR对于两个输入变量:喷油量的质量流速 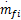
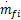
由图2可见, 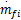

如前文所述,由于发动机两个输入变量的系统过渡过程时间存在严重差异,导致标准二阶Volterra模型无法准确地辨识发动机AFR系统。因而本文对标准Volterra模型进行改进,提出一种变采样间隔的Volterra模型:
y(k)=h0+ 

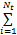
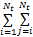
式中:t u为 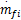
首先,选择采样周期 Ts=0.02 s,使得有足够多的采样样本对系统进行细致描述。此外,为了避免Volterra模型陷入维数灾难,对于较长过渡过程时间的 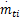
在式(18)中,t u/t v=10,即当k=1时,第1,11,21,…个数据被使用、当k=2时,第2,12,22,…个数据被使用。由此可见,改进后的Volterra模型在保证了所有动态数据信息都被使用的情况下,大大缩短了模型截止阶数,避免了维数灾难带来的困扰。
为了充分激励发动机系统的全部非线性动态特性,本文采用具有白噪声特性的随机幅值序列(Random amplitude sequences,RAS)作为发动机的激励信号。选取20 000个从20°到60°的RAS信号作为发动机输入序列θ,同时选取20 000个从0.0005 kg/s到0.003 kg/s的RAS信号作为发动机输入序列 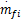
取Modified Volterra模型阶次为二阶,采用带有遗忘因子的递推最小二乘(Recursive least squares,RLS)对Modified Volterra模型参数h0,a u,b u,a v,b v进行训练。RLS既可以保证模型参数的辨识精度,同时也使得模型可以在线辨识修正,实现模型的自适应性。其递推表达式为[ 17]L(k)=
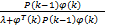 | (19) |
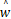
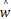
L( k)[ y( k) - φT( k) 
P( k) = 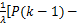
 | (21) |
式中: 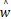
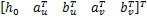
当对 λ, 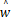
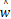
利用上文所述方法,设 P(0) =108 ×I n×n, 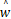
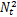
作为对比,图5所示为在相同实验条件下,采用标准二阶 Volterra模型的辨识结果。
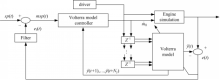
基于Modified Volterra模型SI发动机AFR非线性模型预测控制系统结构如图6所示:
本文所提SI发动机AFR非线性模型预测控制的基本思想是:首先利用前文所得到的SI发动机的Modified Volterra辨识模型对真实系统输出进行N y步预测,并将预测输出序列 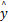
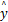
依此类推进入下一个控制循环周期。同时,在每一个控制周期中,利用真实系统的实际输入输出数据对Modified Volterra模型进行在线自适应矫正,并将模型误差反馈给设置点,实现自适应闭环反馈控制。
模型预测是模型预测控制的基础和前提。以上文所得到的SI发动机辨识模型为基础,利用历史输入数据,将辨识模型中的线性部分和非线性部分分开,即可以很方便地构造SI发动机AFR预测模型。
将式(18)改写成[ 18]:
y = Gu u + fu + c (22)
式中: y = 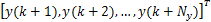
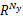
u =
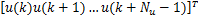 | (23) |
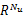
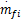
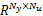
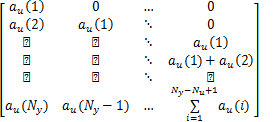
式中: au( i)为前文 Modified Volterra辨识模型中的对应系数。
式(22)中, fu∈ 
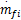
[ u( k) u( k-1) … u( k-Nt +1)]T;
fu( k+2) =[ u( k+1) u( k) 0 … 0]· Bu·
[ u( k+1) u( k) u( k-1) … u( k-Nt +2)]T;
fu( k+3) =[ u( k+2) u( k+1) u( k) 0 … 0]· Bu·
[ u( k+2) u( k+1) u( k) u( k-1) …
u( k-Nt +3)]T
fu( k+4) =… (24)
其中: Bu∈
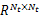 | (25) |
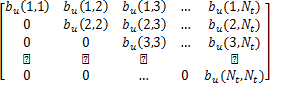
式中: bu( i, j)为前文 Modified Volterra辨识模型中的对应系数。
式(22)中, c∈ 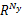
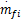
c = cu + cv + h0+ d (26)
式中: cu∈ 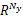
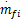
cu = Hu up + gu(27)
式中: Hu up为与过去时刻 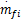

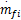
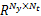
 | (28) |
当 N y
 | (29) |
式(27)中, gu∈
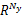 | (30) |
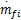
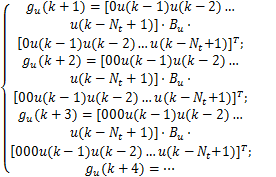
式中: Bu∈ 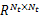
式(26)中, cv∈ 
cv = Hv vp + gv + Gv v + fv(31)
其中 Hv vp为与过去时刻 θ序列相关的线性部分, vp∈ 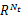
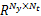
当 Ny =Nt时, Hv =
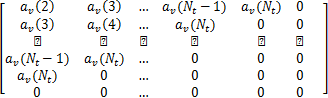 | (32) |
当 Ny
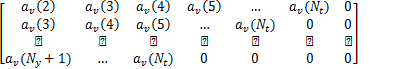 | (33) |
式(31)中, gv∈ 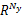
gv( k+1) =[0 v( k-1 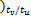
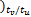
v( k-Nt ×tu /tv 
[0 v( k-1 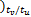
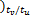
v( k-Nt ×tu /tv 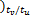
gv( k+2) =[0 0 v( k-1 
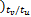
v( k-Nt ×tu /tv 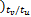
[0 0 v( k-1 

v( k-Nt ×tu /tv 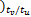
gv( k+3) =[0 0 v( k-1 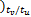
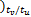
v( k-Nt ×tu /tv 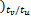
[0 0 v( k-1 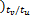
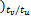
v( k-Nt ×tu /tv 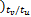
gv( k+4) =… (34)
式中: v 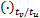

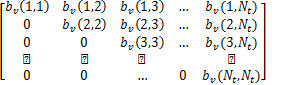 | (35) |
式中: bv( i, j)为前文所述 Modified Volterra模型的对应系数。
式(31)中, Gv v为与未来时刻 θ序列相关的模型线性部分, Gv∈
 | (36) |
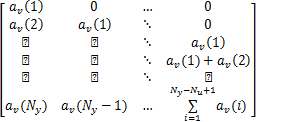
式(31)中, fv∈ 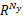
fv( k+1) =
[ 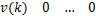
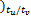
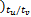
… v( k-Nt ×tu /tv 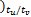
fv( k+2) =[ 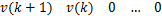
[ v( k+1) v( k 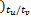
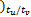
v( k-Nt ×tu /tv 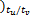
fv( k+3) =
[ v( k+1) 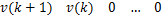
[ v( k+1) v( k+1) v( k 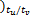
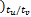
v( k-N t ×tu /tv 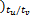
fv( k+4) =… (37)
式(26)中 h0∈ 
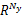
设 u∈ 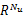
u =
 | (38) |
设 s∈ 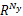
e = s - y (39
) 取最优控制准则为系统的输出与期望值的偏差的平方和最小,即:
J=min[ eT e] (40)
将式(22)与式(39)带入式(40),可得
J =min[ 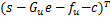
则式(41)的最小二乘解为 :
u =
 | (42) |
式(42)中的最优控制序列 u的求取,实际上是一个滚动优化过程:设当前时刻为 k,首先将上一个控制周期求得的控制序列 u( k-1),利用式(24)计算得到非线性项 fu,然后由式(42)得到新的控制序列 u i(k)。如果控制序列 u满足‖ u i(k)- u i-1(k)‖≤δ,则跳出循环,i为第i次循环,δ为可自由设定的公差。如不满足迭代终止条件,则利用本次循环计算得到的控制序列 u i(k)重新计算非线性项 fu,并利用式(42)计算控制序列。显然这一步的控制序列比上一次循环计算得到的控制误差更小,依次类推,反复迭代直到满足迭代终止条件为止。
该算法的迭代步骤为:
第1步:设 i=1。
第2步:当 i=1, k=1时,随机选取控制序列 u;当 i=1, k≠1时,取 u i(k-1)为初始控制序列;当i≠1,k≠1时,取 u i-1(k)为初始控制序列。并利用初始控制序列计算得到非线性项 fu。
第3步:利用公式(42)计算控制序列 u。
第4步:如果控制序列满足跳出条件‖ u i(k)- u i-1(k)‖≤δ,则跳出循环,并将最优控制序列的第一个控制值给真实发动机;如不满足迭代终止条件,则设i=i+1,并返回第2步重新计算。
由于上述迭代过程实际上是一个最小二乘滚动优化过程,所以该迭代过程的收敛性自然得到保证[ 18]。
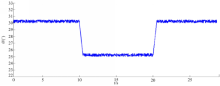
为了验证本文的可行性及有效性, MEVM模型为被控对象,利用 Matlab进行在线仿真实验。如图7所示:
将进气阀开度 θ设为30 °,在t =10 s处经过0 .5 s变化至25 °,并在t =20 s处经过0 .5 s变化至30 °。为了模拟人体正常抖动,在原有信号基础上叠加幅值为0 .5 °的随机噪声信号。
设采样周期为0.02 s,预测步数N y为40,控制步数N u为30,利用本文方法对发动机AFR进行控制。同时,利用当前汽车发动机AFR控制广泛应用的PI控制器对发动机模型进行控制,其控制器表达形式为
[ 16] 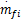
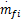
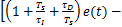
 | (43) |
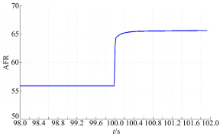
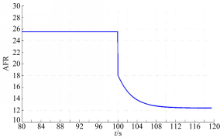
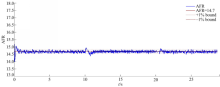
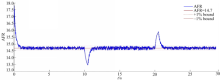
由于当前广泛采用的控制器为PI控制器,故此τD取为0。利用Ziegler-Nichols方法对PI控制器进行参数整定,得到K s=3.28×10-4,τI=0.25 s。并将PI控制器与本文方法的控制效果进行对比,如图8,图9所示:
从实验结果可以看出,本文控制方法的控制效果明显优于传统PI控制器。图8、图9可知,当工作点发生改变时,本文方法具有超调量小,控制过程时间短的特点,均优于目前广泛应用于发动机AFR控制的PI控制器。
针对SI发动机的非线性及对于喷油量的质量流速 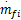
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|